Delta Wing 氣體混合裝置關鍵技術研究

秦明坤，李 強，王建普

（1．菏澤泰諾環境科技有限公司，山東 菏澤 274000；2.菏澤市生態環境局 定陶區分局，山東 菏澤274100）

近年來隨著我國環保力度的持續加大，大量工業爐設備的煙氣NOx排放超標成為繼燃煤電廠及鋼鐵冶金領域煙氣脫硝之后亟待解決的問題，選擇性催化還原（SCR）是當前使用最為廣泛的脫硝技術，SCR 工藝設計的關鍵因素之一是實現還原劑氨與煙氣中氮氧化物的均勻混合，若催化前氨/氮摩爾比分布不均，必會導致局部區域還原劑不足，降低脫硝效率[1]。如何實現噴入氣體與煙氣的快速均勻混合，成為該領域面臨的重要問題。

目前，大型方、圓形截面管道氣體混合多采用格柵式混合器[2]。凌繼紅等人[3]對HEV 型靜態混合器的混合特性進行了實驗和數值計算，分析了各影響因素對其影響；裴煜坤等人[4]設計了一種針對管道截面尺寸較大、混合距離短的V 型噴氨混合器裝置。這些格柵式混合技術雖然應用比較成熟，但卻難以克服噴嘴數量多、 易堵塞等難題。近年來，將Delta Wing 混合器應用于噴氨混合的技術在多個項目中取得了優異效果。它是利用繞流鈍體產生的渦街脫落和渦旋來強化混合，在流體動力學領域有著廣泛的研究和應用基礎[5]，如鈍體穩燃燃燒器[6-7]、強化換熱[8]和提升管氣固混合[9]等。研究表明渦發生器能夠取得較好的多相混合效果，然而，針對Delta Wing 型混合器在脫硝領域的系統性研究不足，該技術在應用過程中仍然存在著很大的盲目性，其關鍵設計參數對其混合特性的影響規律尚不明確，相關問題急待解決。

本文采用Fluent 軟件的組分輸運模型模擬了氣體間混合效果，經過變量的無量綱化，著重考查了不同結構、鈍體堵塞比對氣體混合效果的影響，分析了不同雷諾數對流場和示蹤氣體濃度分布的影響，為Delta Wing 混合器工程應用提供了指導。

1 模型的建立

1.1 幾何模型及流場離散

模型的尺寸、煙氣和混合氣體入口速度、示蹤氣體類型均參照文獻[10]的實驗裝置。以斯特勞哈爾數（Strouhal number）作為相似準則數，討論不同雷諾數（Reynolds number）下的流場分布。雷諾數 Re=UO·d1/υ，斯特勞哈爾數 St=f·d1/UO，UO為來流速度，m/s；f 為渦街脫落的周期頻率，s-1；d1為橢圓長軸，m。

圖1 為結構示意圖，表1 為尺寸及計算參數。煙氣由左側進入管道，來流速度為UO，示蹤氣體以一定速度噴入管道。噴氣的方式分為三種：逆向-鈍體、逆向+鈍體和順向+鈍體。

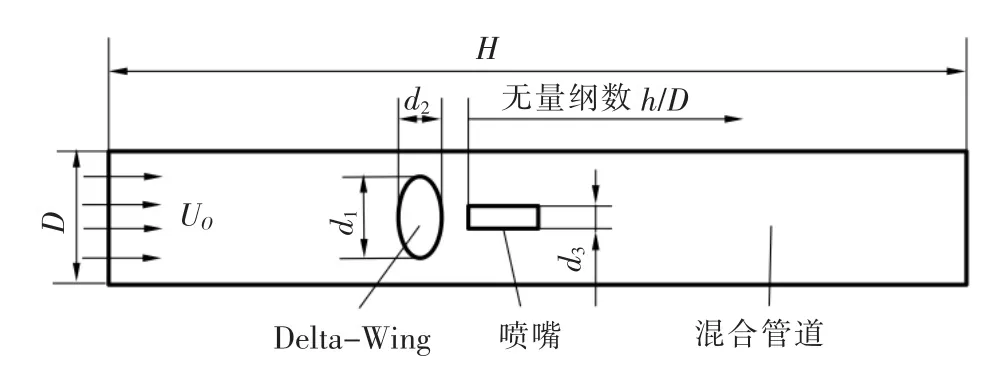
圖1 模型結構示意圖

采用Gambit 對二維模型分區域劃分網格，選用四面體和六面體相結合的網格劃分方法，網格扭曲率均小于0.4。圖2 給出了結構局部關鍵部位網格劃分結果。

表1 數值模擬計算參數表

圖2 局部網格劃分示意圖

1.2 數學模型及數值方法

選用組分輸運模型，載氣為Air，示蹤氣選用CO，研究冷態狀況下的混合行為，Fluent 通過對第i種物質的擴散方程進行計算，得到其質量分數，組分守恒方程如下：

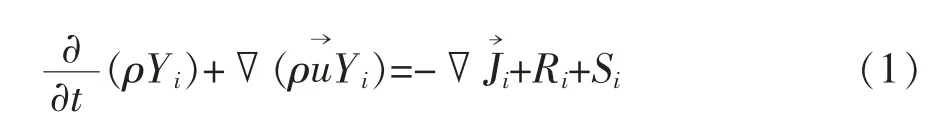
式中：ρ 為主流流體密度，kg/m3；Yi為組分 i 的質量分數；為流體速度矢量，m/s；t 為非穩態時間，s；化學反應的凈生產速率Ri和源項導致的額外產生速率 Si在本模型中均為零。物質 i 的擴散通量由濃度梯度產生，湍流狀態下的擴散通量計算公式如下：

式中：μt為湍動黏度，Pa·s；Di，m為組分 i 在物質 m 中擴散系數，m2/s；湍流施密特數Sct缺省值為0.7。

針對繞流問題的模擬，前人經過模擬和實驗對比結果顯示，采用 RNG k-ε 湍流模型比標準k-ε 模型甚至大渦模型（LES）效果更好[11]，采用非穩態比穩態模擬結果更接近實驗結果[12]，本文采用非穩態RNG k-ε 湍流模型對問題進行計算。邊界條件選用由湍流強度和水力直徑定義的速度入口，出口為outflow，壁面無滑移，近壁面采用標準壁面函數法。

動量離散采用二階迎風差分格式，壓力-速度選用Simple 耦合方式。時間步長為0.005 s，模型選用雙精度求解器進行求解。對出口CO 面平均質量分數進行監視，當曲線發展到水平，或者曲線在一定值范圍上下周期性波動時，認為計算達到收斂。

2 圓孔側噴實驗驗證

本文采用采用無量系數T 將模擬結果同東南大學梁秀進等人的圓孔側噴實驗結果[13]進行比較。計算工況為煙氣量Q=300 m3/h，噴氣量Qx=4.5 m3/h，噴入氣體為 CO 和 Air 的混合氣，CO 質量分數為 0.04； 煙氣為Air。h/D 表示長度/直徑的無量綱數；r/R 為徑向位置的無量綱數。采樣位置h/D=2.2 處的徑向CO 分布情況見圖3，結果顯示CO 濃度分布與實驗結果相符，說明了模擬方法的準確性，可以用來研究氣體混合問題。

圖3 在 Q=300 m3/h，Qx=4.5 m3/h 時CO 分布情況的實驗與模擬結果對比圖

式中 ：Ci為測 點 CO 濃度，mol/m3；Cav為平均 濃 度，mol/m3。

3 結果與討論

3.1 結構和堵塞比對流場的影響

圖4 為繞流鈍體的流場跡線分布圖。結構a 至d為氣體逆向噴入方式，結構e 的噴嘴為順向布置。從跡線的流動特征知，單純的逆向噴入方式a 會造成示蹤氣體發生偏斜，并且擾動主流氣體，使之產生類似渦街的流動，在尾部形成渦團，CO 氣體從渦團中心向外圍擴散，擴散強度較弱，混合效果不夠理想。

圖4 流場跡線圖

本文模擬結果顯示，結構b 的鈍體堵塞比較小（d1/D=0.3），主流氣體在其后面形成的靜壓區不穩定，另外示蹤氣體的噴入會對鈍體后的尾流產生一定影響，使得流動不同于結構a，結果產生圖4 中的渦街流動。堵塞比增大至0.5，有限通道內的鈍體擾流會在后方形成兩個規則的渦眼，渦眼內旋流擾動強烈，可以強化氣體混合，流動狀態穩定。鈍體堵塞比為0.7時，外緣氣體速度較高，使得渦眼中心位置向后偏離。當堵塞比更大時，流動可能還會發生變化。結構e 的渦眼中心位置與c 和d 差別較大，主要原因是示蹤氣體噴射位置和順流噴射方式影響的結果。

3.2 結構和堵塞比對濃度分布的影響

圖5 顯示了氣體間的混合效果，結構a 和b 渦團現象明顯，濃度分布成點渦狀，在尾部形成點擴散源，結構a 的不均勻性一直拖延到h/D=6.5 時仍然存在，而結構b 的不均勻性較短，這主要和非穩態進行時間有關，不同時刻渦點的分布位置也會移動。流場在堵塞比約為0.5 時發生非穩態流動向穩態的轉變，這將有利于流場的穩定流動和設備的穩定運行。結構c、d 和e 在橢圓鈍體后面濃度較高，在尾流渦眼位置與主流氣體形成強烈混合，當距離噴嘴h/D=3 時，濃度分布已趨于均勻。

圖6 為五種結構在位置 h/D=0.4、1.2、2.0 和 2.8處的CO 濃度分布曲線，定量比較了五種結構在相同位置處CO 摩爾濃度的分布情況。類型a 和b 的濃度分布曲線不對稱，沿軸向分布存在較大波動。類型c、d 和e 在截面整體分布均勻，在邊緣濃度值幾乎為零，當距離h/D 大于2.0 時，這種不均勻現象逐漸消失，而a 的不均勻性持續距離較長。在相同位置，堵塞比0.7 比0.5 具有更好的混合效果。此外，順流噴射比逆流能取得更好的混合效果，在h/D=0.8、1.2、2.0 等位置處渦旋內濃度分布均勻。

圖5 CO 體積分數分布云圖

圖6 CO 摩爾濃度分布曲線圖

3.3 結構和堵塞比對壓力損失的影響

壓力損失是制約設備應用的一大因素，本文采用阻力系數Cp[14-15]對繞流產生的壓力損失進行分析，阻力系數越小，經濟性越好。

式中：P 為入口總壓，Pa；PS為出口總壓，Pa。

由圖7 可知，隨著鈍體堵塞比的增加，阻力系數增加，壓力降會顯著升高。另外噴嘴布置位置和混合氣體的流量對阻力系數也有影響。混合氣體流量大、噴射速度高、逆流布置均會增加壓力損失，而順流布置有利于減小阻力損失。

圖7 五種不同方式的阻力系數對比圖

3.4 雷諾數的影響

圖8 為 d1/D=0.7 時，Re 分別為 2 337、9 210、22 368、35 526 下的濃度分布。Re 更低時，混合氣量太小，沒有工業應用的價值[16]，因此不考慮低雷諾數的情況。隨著Re 數的增大，濃度擴散達到均勻的位置向后推移，這是渦旋被高速的主流氣體拉長所致。

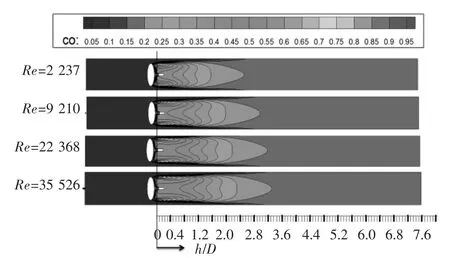
圖8 Re 對CO 體積分數分布的影響圖

本文采用統計學變異系數S 定量描述氣體徑向混合效果，公式如下：

由圖9 知，隨著雷諾數的增大，變異系數增加，CO 濃度分布的不均勻性增加，當h/D 大于4 時，S小于0.05，Re 數的影響作用不明顯，認為混合達到均勻[17]。在本研究的Re 數取值范圍內，低Re 有利于氣體的混合，因為氣體的混合受流動狀態和混合時間的共同影響。Re 低，湍流度小，不利于混合，而氣體在管道中的混合時間延長，使得混合充分。

圖9 Re 對CO 摩爾濃度變異系數S 的影響圖

4 結論

（1）鈍體能夠起到強化氣體混合的作用，尤其在鈍體下游h/D 大于2 的位置，可明顯改善單純逆向噴射氣體的混合不均現象；

（2）堵塞比高于0.5 時，繞流鈍體流場由非穩態轉換為穩態，流場分布較規則，不存在渦街脫落的擾動，有利于氣相流場的穩定流動和設備的穩定運行，并且，隨著堵塞比的增大，混合段長度縮短，混合效果提高，但會造成阻力損失增加；

（3）鈍體堵塞比為0.7 時，示蹤氣體順向噴射能在保證混合效果的前提下，減小鈍體渦眼尺寸，降低阻力損失；Re 數的升高會延長漩渦影響范圍，增大示蹤氣體混合的不均勻性，不利于固定反應段內氣體的混合。