既有裂縫、空洞病害隧道爆破振動安全控制標準*

郭新新，劉錦超，汪 波，喻 煒，王振宇，李浩彬,2

（1. 西南交通大學交通隧道工程教育部重點實驗室，四川 成都 610031；2. 河南省交通規劃設計研究院股份有限公司，河南 鄭州 450052）

伴隨交通道路建設的持續快速發展，既有隧道旁修建新隧道已成為隧道（交通流量）擴容的主要方式。目前，我國交通山嶺隧道以鉆爆法施工為主，當新舊隧道間距較小時，新隧道的爆破施工將不可避免地對既有隧道產生不利影響。因此，制定合理、可靠、準確的振動安全(振速)控制標準，是近接爆破施工中必須解決的首要技術問題[1-2]。關于爆破對地下洞室安全性的影響，已有了大量研究：李洪濤等[3]以混凝土與基巖面的層間抗拉強度為控制基準，研究了體波（P 波）作用下的新澆筑襯砌混凝土的安全振動速度；易長平等[4]采用混凝土抗拉強度作為基準，基于復變函數理論，推導了地震波不同角度作用下的襯砌臨界振速；Jiang 等[5]采用數值模擬方法，研究了隧道襯砌的爆破振動安全判據。但無論采用理論或數值分析的方法，已有研究大多假設既有隧道完好。

實際工程中，既有隧道受地質環境、先期施工過程及后期的運營管理等因素的不利影響，不可避免存在病害，其中以襯砌裂縫和拱頂區域空洞最常見[6-7]。裂縫與空洞的存在，會使襯砌結構的靜態承載能力和動力響應發生變化，易加劇既有隧道結構的安全風險。因此，對于鄰近既有隧道的爆破設計與施工，有必要分析裂縫與空洞對既有隧道襯砌動力響應的影響，具有工程價值。目前，已有考慮襯砌裂縫與背后空洞對既有襯砌動力響應影響的研究：劉敦文等[8]研究了既有隧道拱頂脫空對襯砌動力響應的影響；羅攀峰[9]采用數值模擬方法，研究了不同圍巖級別下不同平面面積和不同部位空洞對襯砌結構動力響應的影響；汪波等[10-11]基于隧道實測裂縫與空洞形態，采用數值模擬詳細研究了，新隧道爆破下不同部位裂縫和空洞、不同擴展深度裂縫和不同大小空洞對既有隧道二襯結構動力響應的影響。但上述研究大多聚焦于分析結構的動力響應，缺乏對最終安全控制標準制定的研究。

本文中，以杭金衢高速公路既有新嶺隧道旁擬建新隧道的具體工程為背景，在對既有隧道襯砌裂縫和背后空洞的分布規律、特征等進行統計與分析的基礎上，系統開展爆破荷載作用下裂縫、空洞對既有隧道襯砌動力響應的影響，并最終提出振速安全控制標準。

1 工程概況

既有新嶺隧道擴容采取了在既有隧道旁新建隧道的技術方案。新隧道為上行、下行獨立分離式雙向六車道隧道（凈寬15.25 m、凈高5.0 m），施工采用鉆爆法。既有隧道為分離式雙向四車道隧道（凈寬10.75 m、凈高5.0 m）。新、舊隧道穿越基本一致，圍巖級別Ⅲ～Ⅴ級，區段內圍巖巖性以粉砂巖和青灰色、夾紫紅色泥質粉砂巖為主，地下水主要為基巖裂隙水。圖1 為新、舊隧道間距示意圖，新建隧道在洞口段距原隧道距離25～35 m，主體洞身段與舊隧道距離約40 m。

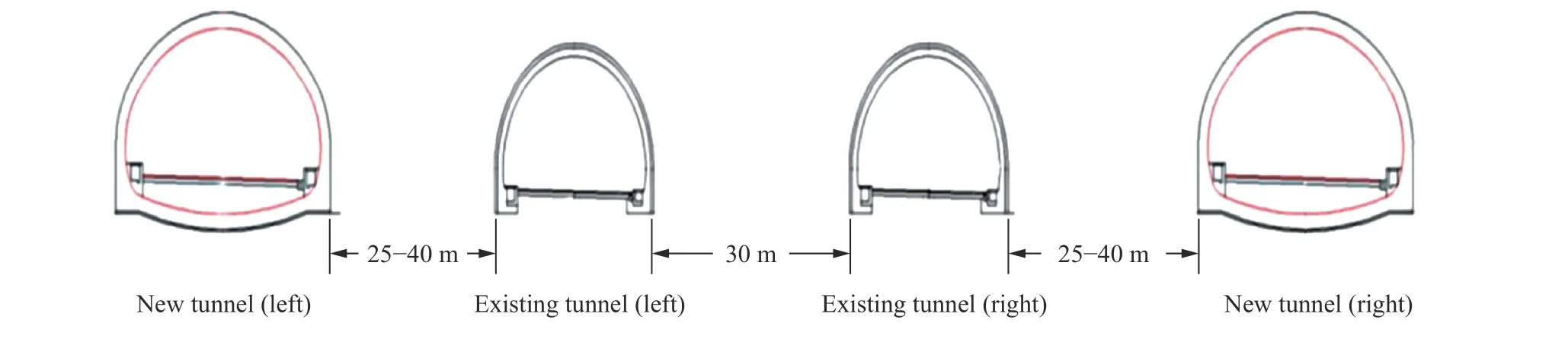
圖1 新老隧道間距Fig. 1 Distances between new and old tunnels

2 病害調研

為了方便數值模擬，采用地質雷達沿隧道縱向對拱頂和左、右拱腰背后的空洞與不密實進行檢測。測定了空洞沿隧道縱向（測線）的分布規律及深度，當測得某點空洞深度大于50 cm時，以該點為基準進一步測量了該處空洞沿隧道橫斷面向尺寸。對肉眼可見的襯砌裂縫采用了刻度放大鏡進行表面開裂寬度檢測，當測得表面開裂寬度大于1.5 mm 時，采用超聲波法測定該處裂縫的徑向深度。最終的統計分析，如圖2～5 所示。

圖2～3 為既有隧道空洞與裂縫沿隧道縱橫向的分布規律：空洞沿縱向主要分布于Ⅲ級圍巖段，占比81%，沿橫向主要分布于拱頂，占比57.5%；裂縫沿縱向主要分布于Ⅲ、Ⅳ級圍巖段，占比55.8%、32.4%，沿橫向主要分布于邊墻、拱腰及拱頂區域。圖中，拱頂-拱腰是指裂縫從拱頂延伸至拱腰位置，拱頂-邊墻是指裂縫從拱頂延伸至邊墻位置，以下類同。

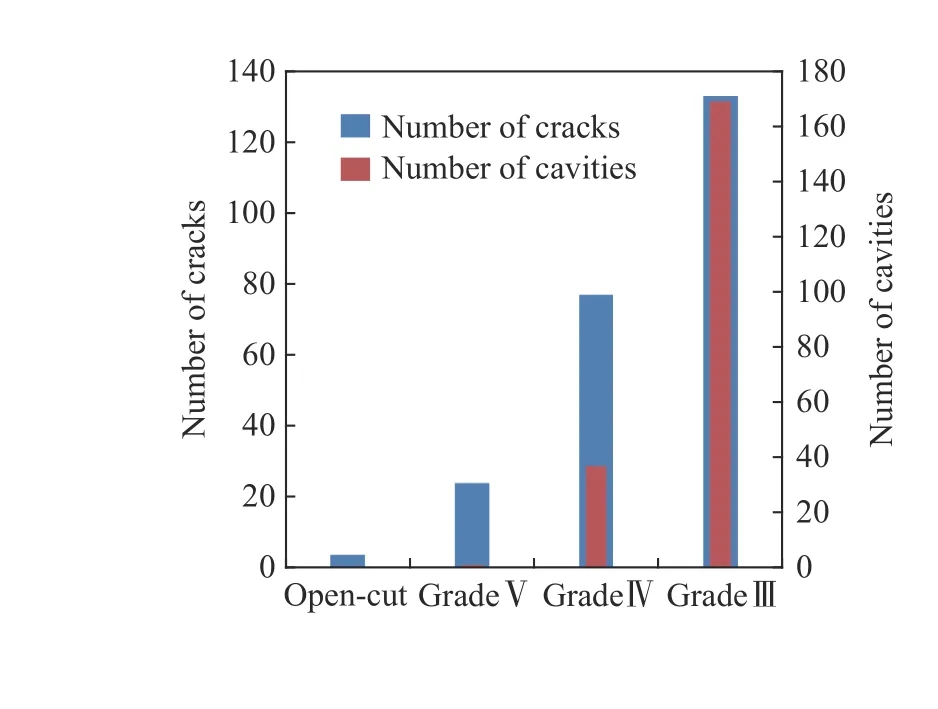
圖2 裂縫、空洞沿縱向分布Fig. 2 Longitudinal distribution of cracks and cavities

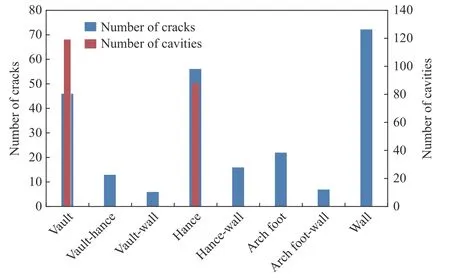
圖3 裂縫、空洞沿橫向分布Fig. 3 Transverse distribution of cracks and cavities

圖4～5 為既有隧道空洞與裂縫特征：空洞深度一般為20～50 cm，極少超100 cm；深度超50 cm 的空洞，環向寬度一般為0～100 cm，極少超200 cm；縱向長度一般為0～10 m，極少超20 m。裂縫(表面) 寬度一般為3 mm 以下，極少超3 mm，均屬微張開裂縫；寬度超2 mm 的裂縫，徑向深度一般為(0～1/4)h（h為襯砌厚度），極少超(3/4)h。

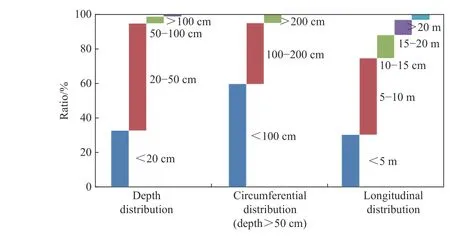
圖4 空洞特征(深度、環向、縱向)Fig. 4 Cavity characteristics (depth, circumferential, longitudinal)

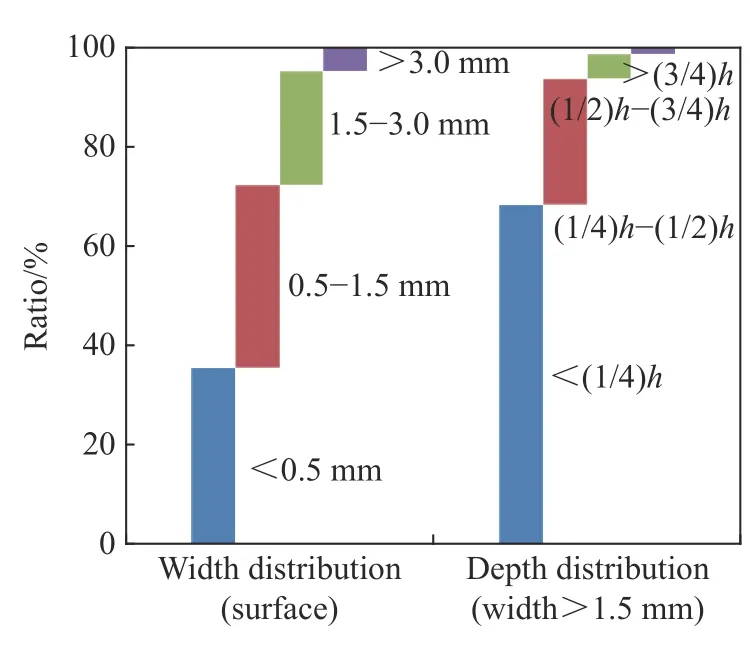
圖5 裂縫特征(寬度、深度)Fig. 5 Fracture characteristics (width, depth)

3 計算和分析

3.1 計算模型和方案

3.1.1 數值模型

采用ANSYS 二維模型，分析裂縫出現部位及徑向擴展深度和空洞橫斷面面積的影響；采用LSDYNA 三維模型，分析空洞沿隧道縱向長度的影響。選取Ⅲ級圍巖隧道斷面，新舊隧道凈距30 m，因此新隧道爆破開挖時，遠端隧道的存在對近端隧道動力響應的影響小，同時遠端隧道受到的振動影響小于近端隧道。為便于計算，選取右線新建隧道和右線既有隧道進行計算。

二維模型如圖6(a)所示，尺寸為135 m×80 m。為避免能量在邊界反射導致計算結果與實際的不符，采用了黏彈性人工邊界，即在邊界節點上施加彈簧-阻尼器元件[12]。各節點的彈簧剛度和阻尼器阻尼系數為：

圖6 計算模型Fig. 6 Computing models

數值計算中，對于空洞的模擬主要有兩種方式：（1）直接在模型中構建“空洞區域”，即不對空洞區域劃分網格；（2）先對全模型劃分網格，再采用單元的“生死”功能，“殺死”空洞區域網格。本文中采用在模型中構建“空洞區域”的方式對空洞進行模擬：如圖7(a)～(b)（拱頂空洞為例）所示，空洞最深點與斷面中心的連線為“徑向線”，空洞深度為H，空洞（環向）寬度B以“徑向線”為基準左右均勻分布。對于裂縫，常用的特征參數主要有位置、深度、長度、寬度等，本文中計算模型為二維平面應變模型，因此選用裂縫位置、表面寬度和深度作為裂縫的基本參數，構建的裂縫模型如圖7(c)（拱頂(1/4)h徑向擴展深度的裂縫為例）所示，裂縫尖端與斷面中心的連線為“徑向線”，裂縫深度為D，裂縫表面寬度C以“徑向線”為基準左右均勻分布。

工程實踐和研究均表明[14-15]，隧道掌子面爆破中，掏槽孔產生的振動效應最大。因此，本文中僅計算掏槽孔段1#（2 號巖石乳化炸藥，藥量11.6 kg）的爆破效應，圖8 為Ⅲ級圍巖斷面掏槽孔設計。將爆破荷載施加于隧道開挖邊界時，常見的荷載峰值計算方法有逐步演算法和經驗公式法。逐步演算法涉及沖擊波到壓縮波至地震波的3 個步驟計算，過程繁瑣，參數眾多，計算結果往往不甚理想。相比而言，經驗公式更易應用，且準確度尚可，因此本文中采用經驗法[16]：

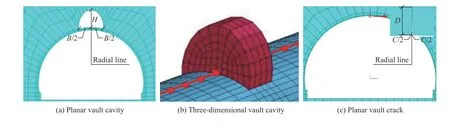
圖7 空洞與裂縫模型Fig. 7 Cavity and crack models

依據爆破振動理論，爆破荷載可簡化為具有線性上升段和下降段的三角形荷載，典型的爆破震動升壓時間為8～12 ms，卸載時間約50～120 ms[17]。本文中，取加載曲線上升段開始時間為0 ms，持續12 ms，下降段結束時間為100 ms，計算總持續時間1.0 s，加載曲線如圖9 所示。

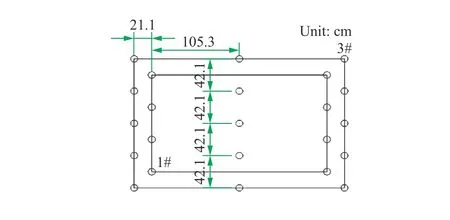
圖8 Ⅲ級圍巖掏槽眼布置Fig. 8 Layout of cut holes for class Ⅲ surrounding rock

圖9 爆破荷載曲線Fig. 9 Blasting load curve

圍巖和襯砌的動強度與靜強度有較大的差別，主要原因是動荷載的瞬時性。依據王思敬等[18]建立的動彈性模量Ed與靜彈性模量Es的轉換公式、戴俊[19]建立的動泊松比 μd與靜泊松比μs的轉換計算公式：

獲得了材料參數，見表1。

闌尾炎在臨床中一種比較常見且多發的急腹癥,臨床表現變化快,極易引起諸多嚴重的并發癥,危害患者的身體健康,故而臨床需盡早診治,以控制病情進展所致的闌尾穿孔。近兩年來,腹腔鏡技術因為微創、術后康復快等優勢而在臨床治療闌尾炎患者中備受青睞,但手術治療期間的護理配合也是提高臨床療效的關鍵[1]。對此,本文以筆者所在醫院收治的闌尾炎腹腔鏡手術患者70例為研究對象,特此分析了優質護理服務的方式與效果。現做如下報道:

表1 材料參數Table 1 Material parameters

3.1.2 計算方案

先設計裂縫隧道的計算方案。既有新嶺隧道裂縫以縱向及微張開裂縫類型為主，橫斷面上主要出現在邊墻、拱腰及拱頂，沿隧道方向上主要位于Ⅲ級圍巖段。因此，選定Ⅲ級圍巖段，采用二維計算模型，裂縫寬度C取0.3 mm，研究裂縫橫斷面分布位置、徑向擴展深度的影響，通過工況K2-1 獲取最不利工況，再通過工況K2-2 給出振速控制標準。

再設計空洞隧道的計算方案。既有新嶺隧道空洞徑向深度20～50 cm，縱向分布長度以0～10 m 為主，橫斷面上主要出現于拱頂和左、右側的拱腰，沿隧道方向上主要位于Ⅲ級圍巖段。因此，選定Ⅲ級圍巖段，采用二維計算模型，研究空洞橫斷面分布位置、平面面積的影響，通過工況K3-1 獲取最不利工況，再通過工況K3-2 給出振速控制標準。再以此為基準，進一步采用三維計算模型，分析空洞縱向長度的影響（工況K3-3）。

具體計算工況見表2，表中h為二次襯砌厚度，小空洞面積為4.45 m2（寬B=2.7 m，高H=2.0 m），大空洞面積為 16.23 m2（寬B=5.5 m，高H=3.5 m）。通過工況K2-2、K3-2，逐步增大爆破藥量（以Q=1.5 kg 對應的荷載峰值pm0為基數），直至結構應力值增至控制上限。

表2 計算工況詳述Table 2 Detailed simulation conditions

3.2 最不利裂縫

爆破引起的動力響應可分為兩部分。（1）振速響應：一般有合速度與分速度之分，參照GB 6722—2014《爆破安全規程》[20]第13.2.2 節表2《爆破振動安全允許標準》，本文中振速響應分析采用分速度；（2）應力響應：爆破荷載作用下，混凝土襯砌的破壞以拉伸破壞為主[21]，同時本文計算表明襯砌的S3應力（壓應力）遠小于材料抗壓強度，因此應力響應的分析采用S1應力（拉應力）。

如圖10(a)～(b)所示，相比完整工況，不同位置和深度的裂縫對既有隧道襯砌振速響應的影響小。如圖10(c)所示，迎爆側右邊墻出現裂縫時，S1應力最大值明顯增大，且隨裂縫深度的增加而增大；裂縫深度為(1/4)h，斷面S1應力最大值為1.13 MPa；裂縫深度(3/4)h，斷面S1應力最大值增至1.35 MPa。上述分析表明，裂縫對襯砌斷面的影響主要表現為S1應力響應的增強，且隨裂縫深度增加S1應力響應增強，振速響應則基本不變。圖中，x、y為平面坐標系中的水平與垂直方向，下同。

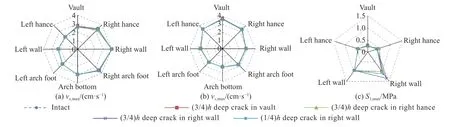
圖10 工況K2-1 下vx、vy 振速極值和S1 應力極值的分布Fig. 10 Distributions of vx, vy and S1 extremum under K2-1 working condition

3.3 最不利空洞

如圖11(a)～(b)所示，相比完整工況，不同位置和平面面積的空洞對既有隧道襯砌振速響應的影響按強弱順序為拱頂、左拱腰、右拱腰，平面面積越大影響越大。以拱頂測點為例：拱頂小空洞，斷面vx,max、vy,max為2.6、4.0 cm/s；拱頂大空洞，斷面vx,max、vy,max增至2.75、10.00 cm/s。如圖11(c)所示：空洞對既有襯砌S1應力極值的影響集中于上半斷面，表現為空洞區域內襯砌S1應力極值增加，區域附近S1應力極值減小；斷面S1應力最大值（1.0 MPa）位于迎爆側右邊墻；空洞平面面積增大對空洞處測點S1應力極值的影響減小。以拱頂測點為例：拱頂小空洞，拱頂測點S1應力極值為0.75 MPa；拱頂大空洞，拱頂測點S1應力極值減至0.46 MPa。上述分析表明：空洞對襯砌斷面的影響主要表現為振速響應的增強，隨著平面面積的增加而增強；斷面S1應力最大值出現于迎爆側邊墻處，不同工況下保持不變。

圖11 工況K3-1 下vx、vy 振速極值和S1 應力極值的分布Fig. 11 Distributions of vx, vy and S1 extremum under K3-1 working condition

3.4 控制標準

通過對裂縫和空洞的最不利工況的研究，可知：最不利裂縫工況K2-2 為(3/4)h深右邊墻裂縫工況；最不利空洞工況K3-2 為拱頂大空洞工況。完整工況K1-1、最不利裂縫工況K2-2 和最不利空洞工況K3-2 下，斷面vmax（max{vx,max,vy,max}）、S1,max與荷載峰值的倍數n的關系如圖12 所示，斷面vmax與S1,max關系如圖13 所示。

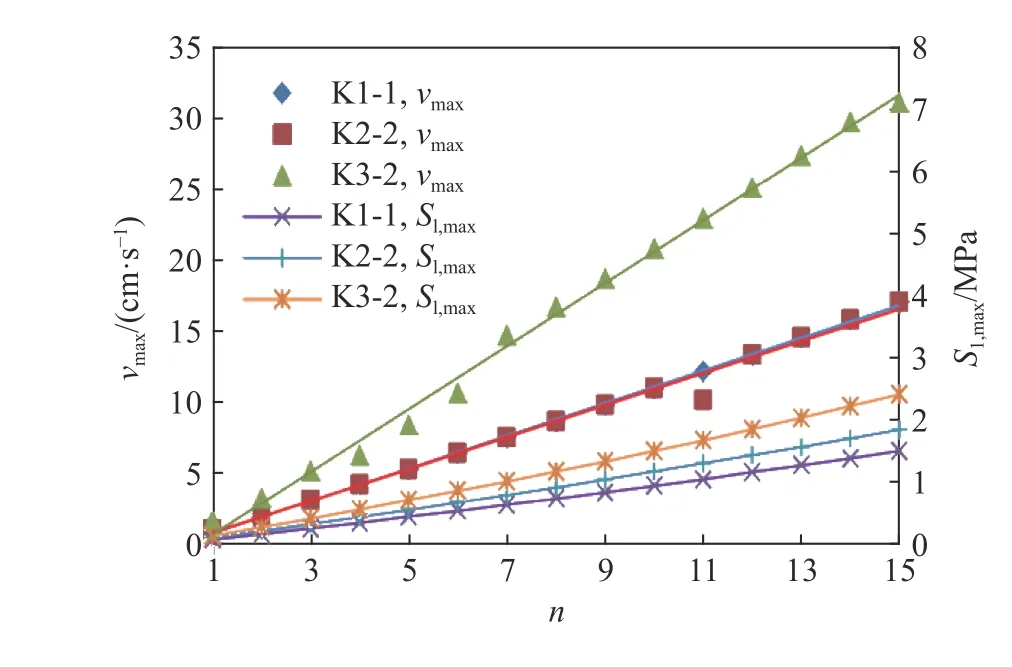
圖12 斷面vmax、S1,max 與n 的關系曲線Fig. 12 Relationship curves of vmax, S1,max and n

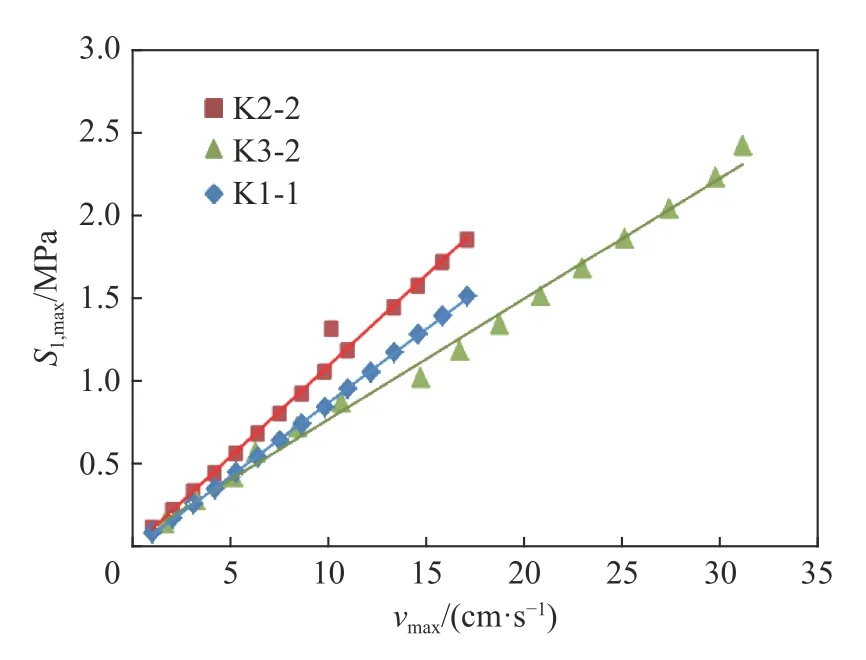
圖13 斷面S1,max 與vmax 的關系曲線Fig. 13 Relationship curves of vmax and S1,max

對于C25 混凝土，其抗拉設計值一般為1.3 MPa[21]，考慮隧道混凝土襯砌強度與時間的相互關系[22]取折減因數0.8，設定抗拉強度(S1應力)允許值為1.04 MPa。代入圖13 進行插值計算：完整工況的斷面vmax為12 cm/s，與《爆破安全標準》[20]規定比較一致，佐證了計算的可靠性；最不利裂縫工況的斷面vmax為9.8 cm/s；最不利空洞工況的斷面vmax為15 cm/s（＞12 cm/s），仍取12 cm/s。

3.5 標準管理體系構建

3.5.1 裂縫標準管理體系

爆破動荷載作用下，襯砌裂縫主要影響結構S1應力的響應，且與裂縫深度相關。因此，以裂縫深度為控制指標，獲取不同裂縫深度下斷面S1應力最大值的變化曲線，如圖14 所示。

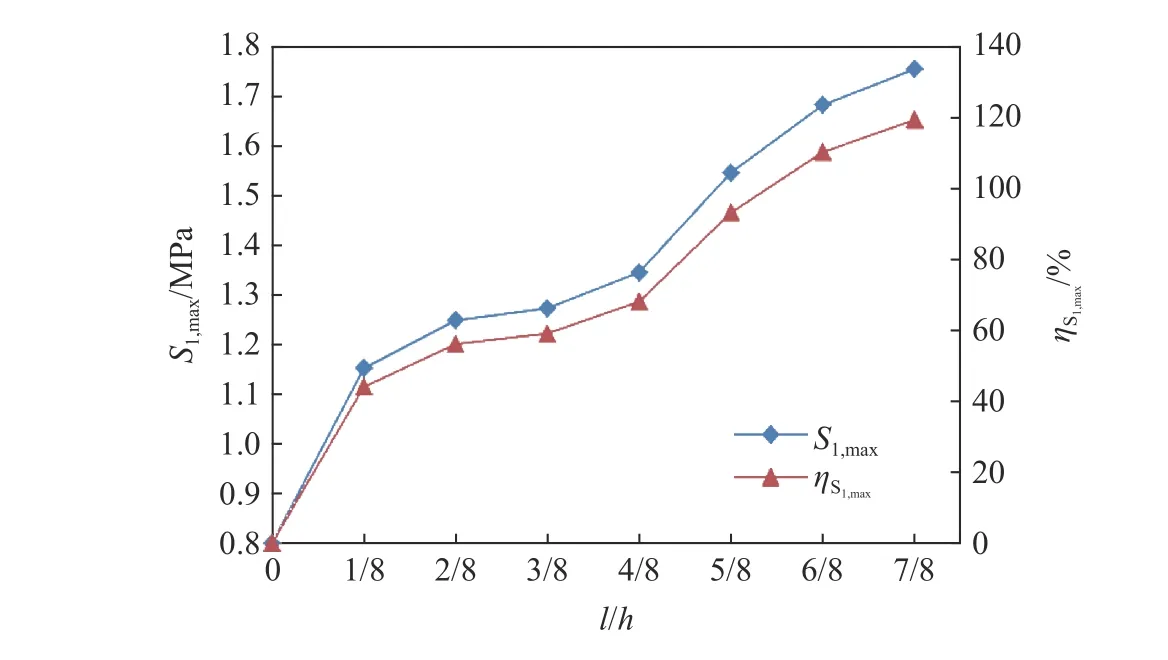
圖14 斷面S1,max 和增幅與裂縫深度的關系曲線Fig. 14 Relationship curves between S1,max, increase of S1,max and fracture depth

由圖14 可見：裂縫深度小于(1/8)h時，隨深度增加，斷面S1應力最大值增大明顯；裂縫深度為(1/8～1/2)h時，斷面S1應力最大值基本不變，曲線平穩；裂縫深度大于(1/2)h時，隨深度增加，斷面S1應力最大值再次增大明顯。以不同深度裂縫的斷面S1應力最大值和增幅為基準，劃分裂縫管理等級，見表3。

表3 裂縫管理等級Table 3 Crack classification

3.5.2 空洞標準管理體系

爆破動荷載作用下，空洞對襯砌的應力響應和振速響應均有影響，以對振速響應的影響為主，且與空洞平面面積相關。因此，以空洞平面面積為控制指標，獲取不同空洞平面面積下的斷面vmax變化曲線，如圖15 所示。

由圖15 可見，隨著空洞平面面積的增加，斷面vmax的變化可劃分為3 個區域時：面積小于5 m2時，斷面vmax基本不變；面積為5～10 m2時，斷面vmax快速增大；面積大于15 m2時，vmax又基本不變。

空洞作為三維結構，制定(振速)安全控制標準過程中，必須考慮空洞沿隧道縱向長度的影響。為此，采用三維計算模型，開展了不同縱向長度L的空洞(縱向)影響區域分析。影響范圍R為較完整工況出現振速增大的縱向長度，放大倍數μ為影響范圍與空洞(縱向)長度之比。

如圖16 所示，空洞縱向長度增加，影響范圍逐漸增大，而放大倍數則逐漸減小。空洞縱向長度以7 m 為界，超過7 m，放大倍數逐漸趨于1。因此，以7 m 為界，定義空洞區域的縱向監控長度：空洞縱向長度小于7 m 時，按3～4 倍縱長進行監測；空洞縱向長度大于7 m 時，按1.0～1.5 倍縱長進行監測；縱向長度小時，倍數取大值。綜合對空洞平面面積和縱向長度的分析，劃分空洞管理等級，見表4。

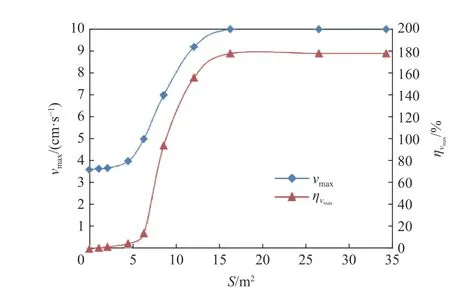
圖15 vmax 和增幅與空洞平面面積的關系曲線Fig. 15 Relationship curves between vmax,increase of vmax and plane area of cavity

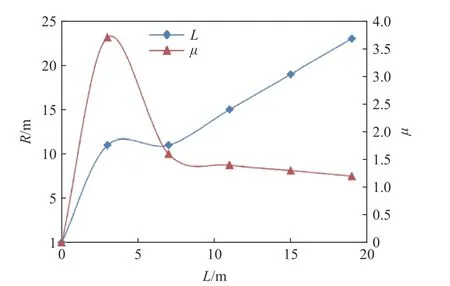
圖16 影響范圍、放大倍數與空洞縱向長度的關系曲線Fig. 16 Relationship curves between influence range,magnification and longitudinal length of cavity

表4 空洞管理等級Table 4 Cavity size classification

4 結 論

以杭金衢高速公路既有新嶺隧道旁擬建新隧道的具體工程為背景，在對既有隧道襯砌裂縫和背后空洞的分布規律、特征等進行統計與分析的基礎上，系統開展爆破荷載作用下裂縫、空洞對既有隧道襯砌動力響應的影響，提出了相應振速安全控制標準。具體結論如下。

（1）裂縫對襯砌斷面的影響主要表現為S1應力響應的增強，且隨裂縫深度增加S1應力響應增強，振速響應則基本不變。以襯砌斷面S1應力最大值為控制基準，劃分裂縫管理等級如下：裂縫深度為(0～1/8)h時，振速限值為12 cm/s；裂縫深度為(1/8～1/2)h時，振速限值為10 cm/s；裂縫深度大于(1/2)h時，振速限值為8 cm/s。

（2）空洞增強了襯砌的振速響應與應力響應，但振速增量明顯大于應力增量。以襯砌斷面S1應力最大值為控制基準，劃分空洞管理等級如下：空洞隧道的振速限值統一為12 cm/s，與完整隧道振速限值一致；空洞縱向長度小于7 m 時，監控范圍為3～4 倍縱長；空洞縱向長度大于7 m 時，監控范圍為1.0～1.5 倍縱長；縱向長度小時，倍數取大值。