后坐阻力激勵下艦炮炮架響應與甲板基座支反力分析
邱群先,劉可可,高 博
(中國船舶重工集團公司第七一三研究所,河南 鄭州 450015)
0 引 言
艦炮發射率高,發射時后坐部分的后坐行程相對短,后坐復進時間短,后坐阻力相對較大。發射瞬時后坐部分能量通過反后坐裝置提供的后坐阻力做功吸收,而反后坐裝置產生的后坐阻力則經由搖架、耳軸傳遞到炮架上,并經過對炮架的沖擊作用后傳遞到艦艇甲板基座。炮架作為艦炮的主承力結構,上部支撐發射系統等部組件,下部通過轉盤軸承與艦艇甲板基座固連。炮架在艦炮發射時后坐阻力激勵下的動態應力、動態變形對艦炮射擊精度具有一定影響,動態加速度對安裝在炮架上的電子元器件、機構、零件等的抗加速度沖擊有著一定影響,后坐阻力通過炮架彈性變形吸能進而傳遞到甲板基座對艦炮的適裝性有著一定影響。因此,艦炮炮架在艦炮總體設計中占有重要位置,設計之初即分析后坐阻力激勵下艦炮炮架的響應對實現艦炮的技術指標、提供甲板基座受力等安裝要素具有重要意義。因使用環境、使命任務、使用方式等方面的不同,艦炮炮架設計與陸炮炮架有著較大差異。當前對于艦炮炮架的設計研究大多集中在靜力分析方面,動態分析研究的文獻尚不多見。文獻[1 - 2]僅對艦炮炮架模態進行了分析,文獻[3]基于Ansys軟件對某艦炮托架的模態進行了分析,對后坐阻力激勵下托架的動態響應進行了仿真。總體來看,對于后坐阻力激勵下,整個艦炮炮架的響應分析工作很少涉及,對于后坐阻力傳遞到甲板基座上的作用力尚未見到研究文獻。本文通過對艦炮炮架在后坐阻力激勵下的響應分析,可以讓設計人員加深對傳統上視炮架為剛體、以最大后坐阻力校核設計帶來的不足。同時,可以讓設計人員對后坐阻力傳遞到甲板基座后的力的分布及其幅值提供途徑,有助于對艦炮最大后坐阻力的理解與認識。
1 炮架模型與后坐阻力
炮架結構是根據艦炮總體功能、性能要求進行設計的。圖1是其三維模型,以B面中心為坐標原點,垂直A面為x軸方向(等同1方向),平行于A面為y軸方向(等同2方向),垂直于B向上為z軸方向(等同3方向)。為研究方便對炮架模型進行了一定的簡化處理,忽略了部分小尺寸結構,并將轉盤軸承等效成結構體成為炮架的一部分。整個炮架材料為Q345,質量5.82 t。A面為水平射擊時炮架承受后坐阻力的受力面,B面為與甲板基座配合的安裝面。炮架長4 m,寬3 m,高1.74 m。A面總面積為0.08 m2,B面為一外徑為Φ2.6 m、內徑為Φ2.2 m的圓環。初始邊界條件為水平射擊,B面固支,A面受到隨時間變化的后坐阻力,如圖2所示。后坐總時間0.15 s,最大后坐阻力45 t。
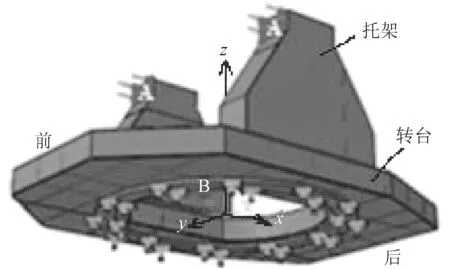
圖 1 炮架模型Fig. 1 Model of gun carriage
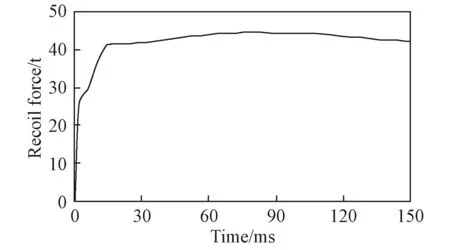
圖 2 后坐阻力與時間關系曲線Fig. 2 Curve of recoil vs. time
2 炮架模態分析
在對后坐阻力激勵時炮架響應分析之前必須首先對炮架的固有模態進行分析。在確定結構的炮架模型及B面約束條件下,采用有限元軟件的振型疊加法進行分析,為保證在頻率提取分析步中提取了足夠數量的模態,先按照300階進行計算。分析得到的300階固有頻率曲線如圖3所示,炮架前10階固有頻率依次為69.149,69.761,156.89,160.31,212.35,226.15,278.62,295.62,42.79,349.07 Hz,第43階固有頻率為1 004.4 Hz,第170階固有頻率為2 004.7 Hz,第300階固有頻率為2 662.8 Hz。圖4為炮架固有頻率階次與有效質量的關系圖,從中可以看出,前50階固有頻率對總有效質量超過了炮架模型可運動質量的85.6%以上,因此取50階模態已足夠使用振型疊加法求解炮架的動態問題。
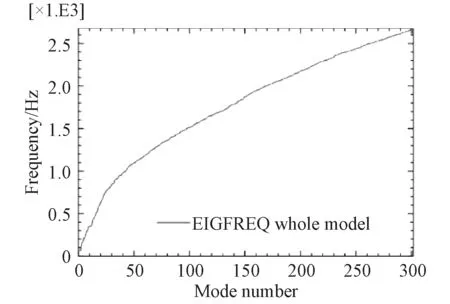
圖 3 各階固有頻率曲線Fig. 3 Curve of frequency vs. mode number
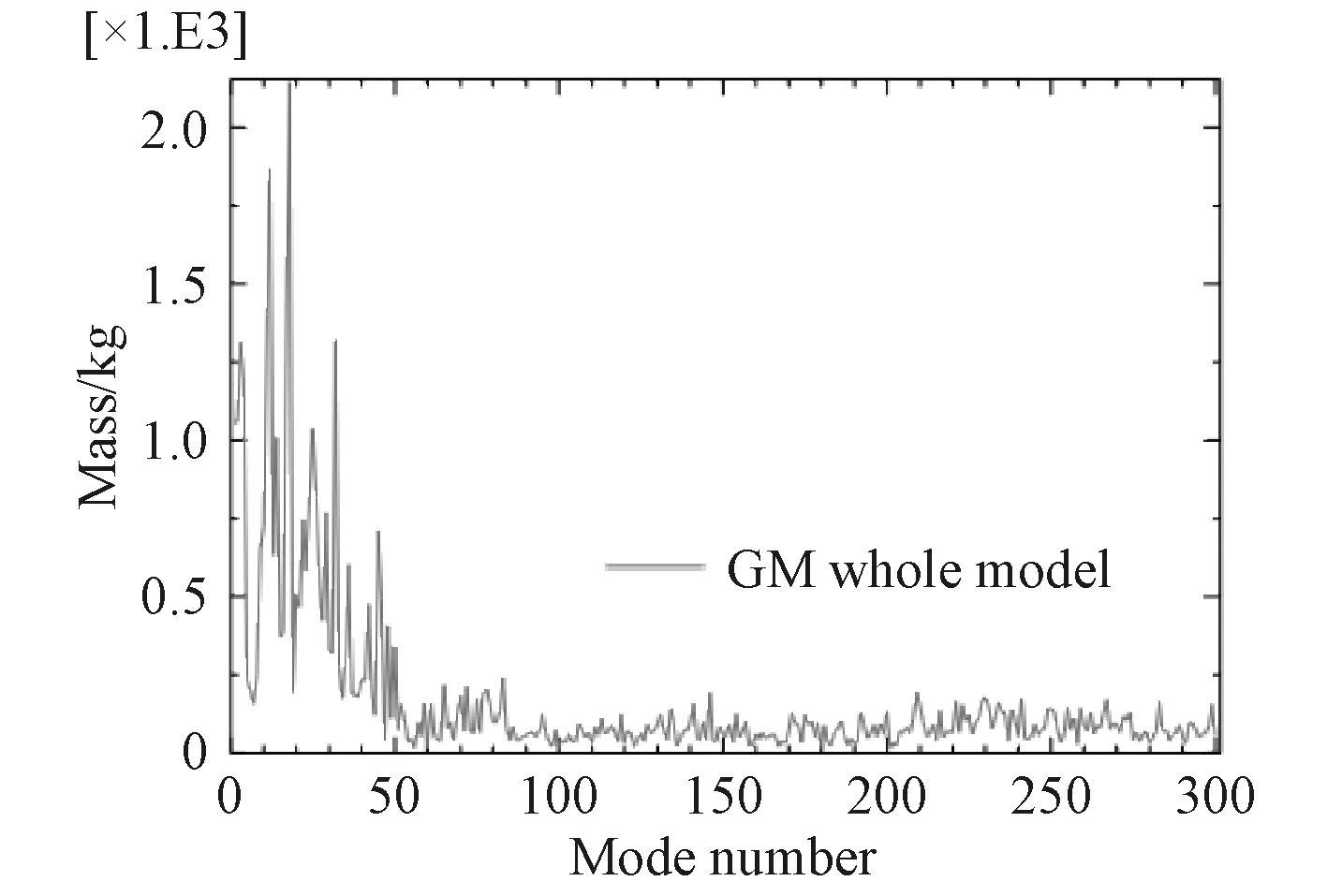
圖 4 各階固有頻率與總有效質量的關系圖Fig. 4 Curve of effective mass vs. mode number

圖 5 各階振型與參與系數曲線Fig. 5 Curve of participation factors vs. mode number

圖 6 各階振型與參與系數曲線Fig. 6 Curve of effective mass vs. three mode number
圖5 為前100階次振型在1,2,3方向的參與系數仿真曲線圖,圖6為前100階次振型在1、2、3方向的有效質量曲線圖。根據仿真結果,50階以上的振型在3個平動自由度上的參與系數與激活的有效質量都相對較小,進一步說明實際研究時取前50階模態確實是可行的。為說明問題,取前100階模態進行分析。第3,5,18,28,29,45階振型在x方向起主導作用,第1,8,14,20,21,47階振型在y方向起主導作用,第6,10,11,36,56,100階振型在z方向起主導作用;第3,18階振型在x方向激活的有效質量起主導作用,第1,14,21階振型在y方向激活的有效質量起主導作用,第6,11階振型在z方向激活的有效質量起主導作用。綜合而言,第1,3,11,18階振型所激活的有效質量最為顯著,分別達到2 213 kg,2 337 kg,2 132 kg,1 631 kg,分別占炮架總質量的38%,40%,36%,28%,因此工程中需要重點關注。盡管56、100階振型在z方向上的參與系數較高,但由于固有頻率已高達1 146 Hz,1 512 Hz,振型所激活的有效質量僅有21 kg,24 kg,對炮架的動態效應所起的作用已不大。
圖7~圖10分別為炮架第1,3,11,18階振型對應的位移云紋圖。從圖中可見,1階頻率下,炮架的左右托架上部朝左右(近似垂直紙面方向)的變形趨勢最大,說明左右托架更易于在左右方向產生振動彈性變形,而炮架下部的轉臺基本處于深色區域,不容易受到該階頻率時的振動影響;3階頻率下,炮架的左右托架上部朝炮架前后方向(紙面的左右方向)的變形趨勢最大,同時炮架的轉臺前后部也呈現出前后方向的變形趨勢;11階頻率下,炮架的左右托架上部朝上下方向的變形趨勢最大,轉臺的左右兩側部呈現出向上、向下的變形趨勢;18階頻率下,炮架的左右托架呈現出的變形趨勢與3階頻率下相似,炮架下部轉臺的變形則由前后部向左右部分轉移。綜合而言,在有顯著質量的激勵的4個頻率時,炮架的托架更易于產生振動變形,這也是需要炮架設計必須重點關注的地方。
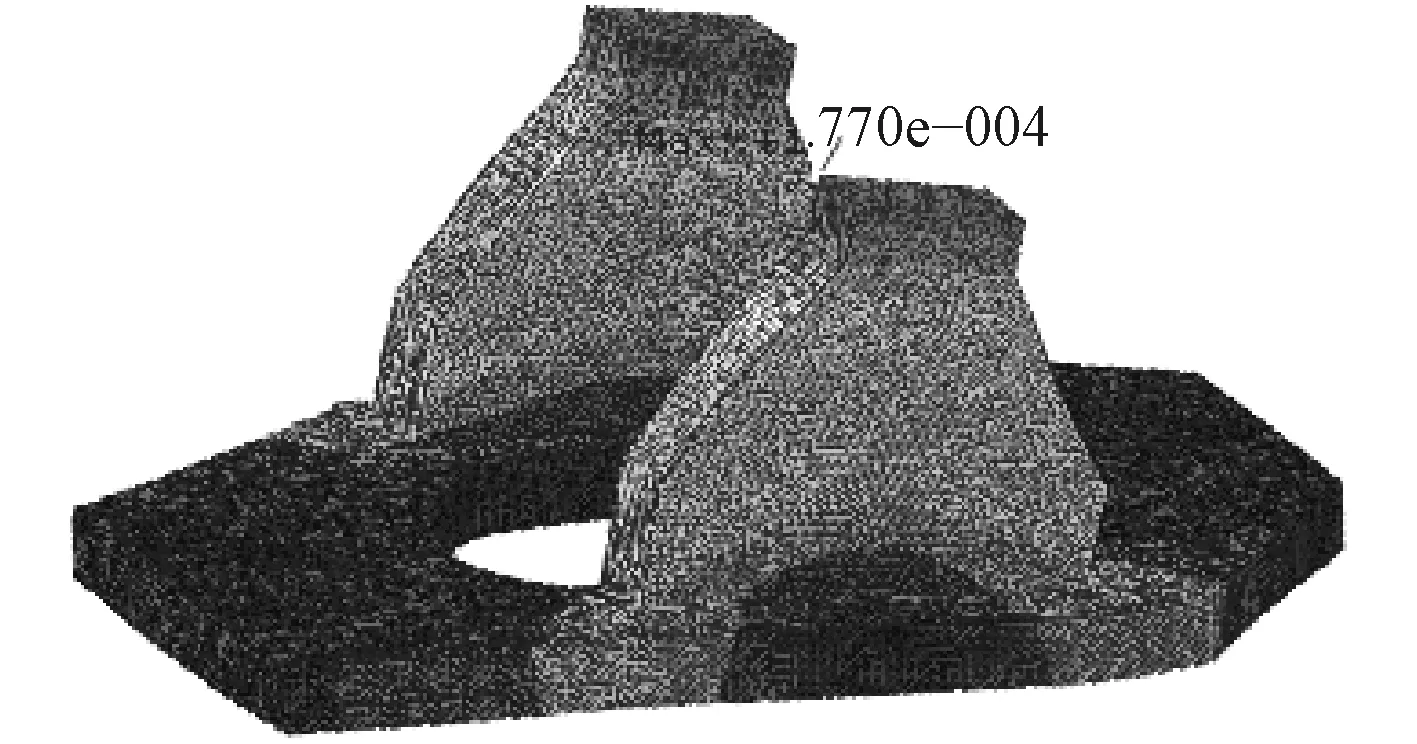
圖 7 第1階振型的位移云紋圖Fig. 7 Displacement contour of 1st mode
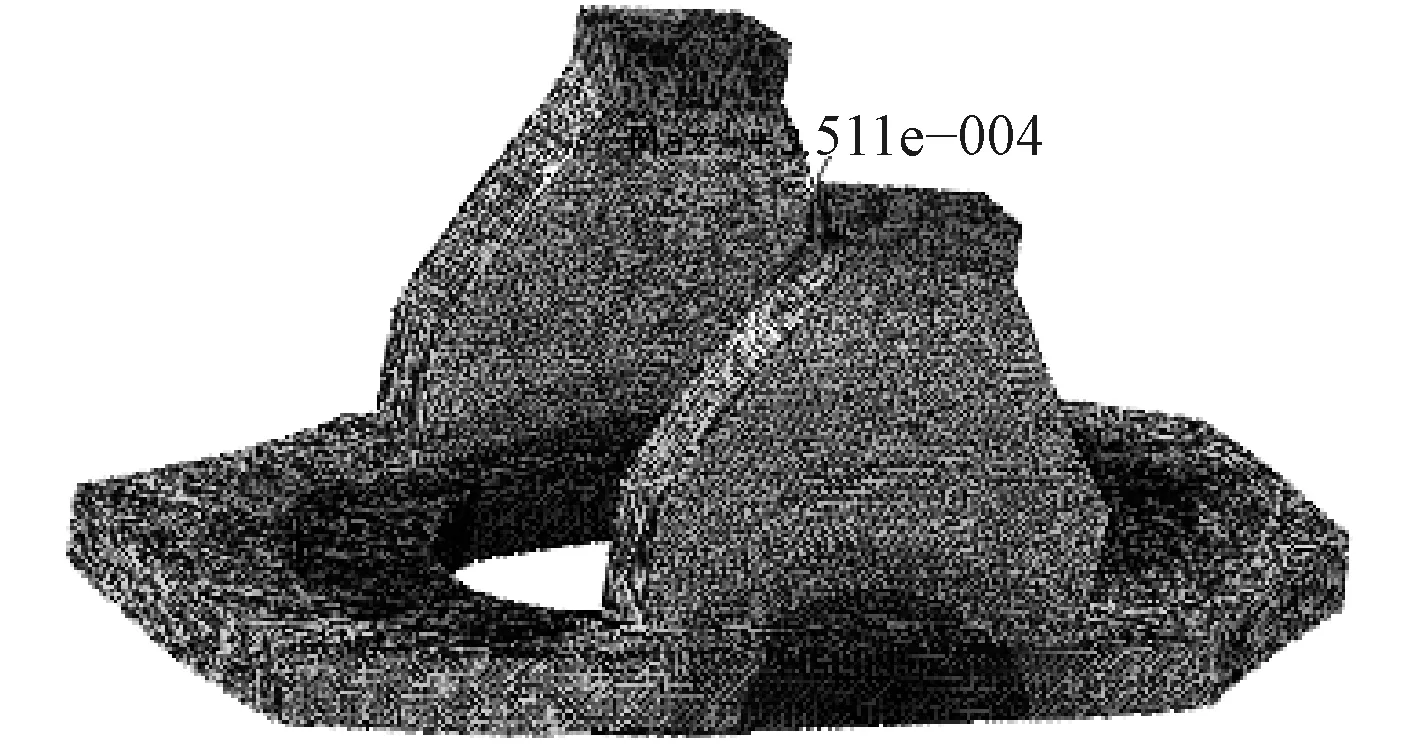
圖 8 第3階振型的位移云紋圖Fig. 8 Displacement contour of 3rd mode

圖 9 第11階振型的位移云紋圖Fig. 9 Displacement contour of 11th mode

圖 10 第18階振型的位移云紋圖Fig. 10 Displacement contour of 18th mode
3 炮架瞬時模態動態分析
在炮架模態分析基礎上,通過在A面施加隨時間變化的后坐阻力,可以得到炮架的瞬時模態動態響應數據。后坐總時間為0.15,為觀察炮架在后坐阻力激勵后的響應,設定分析步時間為0.4 s,B面固支約束。后坐阻力瞬時作用時,最大應力出現在轉臺底部、正對托架與轉臺交接的豎里面位置,并與B面外圓柱面相交的節點(編號3337),該節點的Mises應力隨時間變化曲線如圖11所示。最大應力136.8 MPa,出現在0.017 s時刻。而以最大后坐阻力加載到同樣模型進行靜力學分析,最大應力同樣出現在節點3337號,幅值為59.5 MPa,動態與靜態分析結果比值為2.3:1。最大加速度、最大速度、最大變形的節點編號為478,位于托架頂面四邊形的頂點部位,其中最大變形0.63 mn,出現在0.0108 s時刻,而以最大后坐阻力加載到同樣模型進行靜力學分析,最大變形同樣出現在節點478,幅值為0.29 mn,動態與靜態分析結果比值為2.17:1。最大速度0.493 m/s,出現在0.152 s時刻,最大加速度756.4 m/s2,出現在0.150 6 s時刻。最大加速度、最大速度出現的時刻符合運動學規律,盡管加速度很大,但由于時間短暫,僅有0.000 5 s左右,因此節點產生的速度并不大。圖12~圖14給出節點478的位移、速度、加速度的絕對幅值隨時間的變化關系,從圖中可以看出,在后坐阻力突然增加、突然撤銷時,節點的位移、速度、加速度都有一個突然變化,這是動態分析與靜態分析的最大不同,幅值仿真曲線與節點x,y,z單向仿真曲線可以為實際測試提供依據。
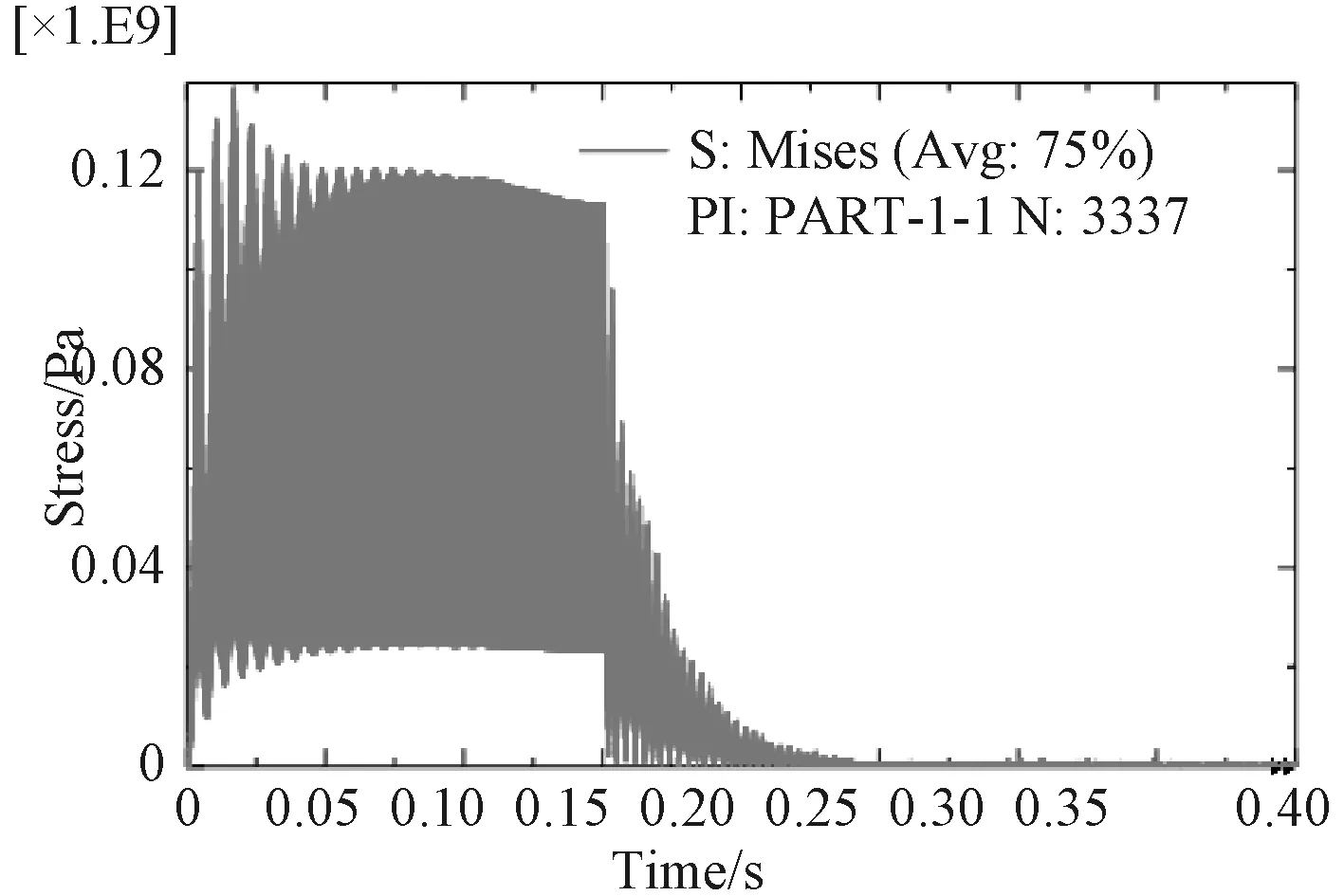
圖 11 最大應力點的應力時間曲線圖Fig. 11 Curve of stress of node 3337 vs. time

圖 12 最大位移點的位移時間曲線圖Fig. 12 Curve of displacement of node 478 vs. time
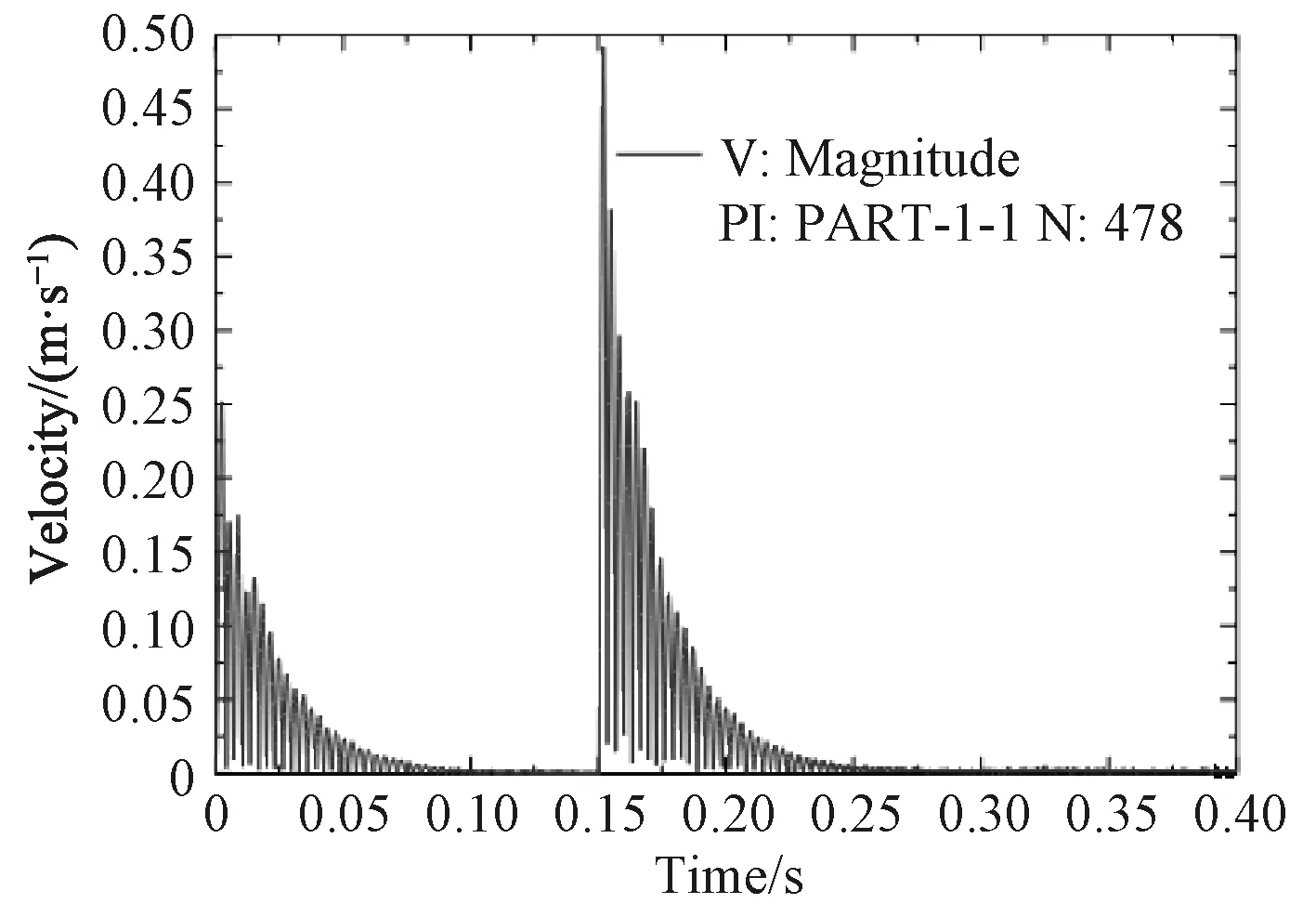
圖 13 最大速度點的速度時間曲線圖Fig. 13 Curve of velocity of node 478 vs. time
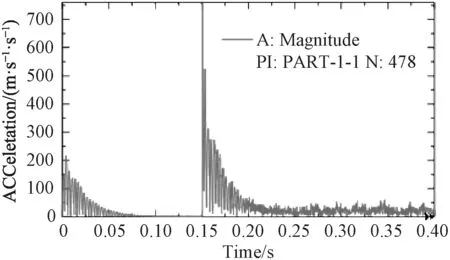
圖 14 最大加速度點的加速度時間曲線圖Fig. 14 Curve of acceleration of node 478 vs. time
后坐阻力對炮架的激勵過程是被離散化成有限個質量單元的炮架的各個網格單元運動狀態發生連續變化的動態過程,網格單元產生加速度,隨著時間的持續,網格單元具有了一定的速度進而帶來各節點位移的變化。因此,后坐阻力對炮架的激勵過程,實際上是按照各階振型不斷振動的過程,激勵過程為0.15 s,振動在0.275 s時刻完全結束。振動過程伴隨著能量的消耗,前文已明確在1,3,11,18階振型時激活的有效質量最為顯著。真實激勵加載后,這4階振型各自所激起的動能隨時間曲線如圖15所示。從圖中可以看到,第3階振型下激起的瞬時最大動能達156.9 J,而1,11,18階振型下激起的動能極小,基本都不超過1 J。由此可以判斷,對于該炮架需要重點關注第3階振型,即平行于后坐阻力方向的振型。圖16為炮架振動過程中的主要能量隨時間變化的曲線圖,整個模型的總平衡能量(ETOTAL)始終為0,表明計算過程穩定,結果比較可信。后坐阻力做功(ALLWK)最大峰值341.4 J,能量平衡后保持259.1 J不變。后坐阻力持續做功期間,伴隨著炮架單元彈性應變能(彈性勢能)和動能的產生,會抵消一部分后坐阻力做功。最大彈性應變能(ALLSE)299.6 J,后坐阻力突然撤銷時為207.2 J,上之后到0.25 s時衰減到0;最大動能(ALLKE)171.6 J,后坐阻力突然撤銷時為171.6 J,之后到0.25 s衰減到0。

圖 15 四階振型對應的動能時間曲線圖Fig. 15 Curve of energy of four modes vs. 17:49:45

圖 16 振動過程中主要能量時間曲線圖Fig. 16 Curve of main energy during vibration
4 后坐阻力傳遞到甲板基座的支反力分析
最大后坐阻力是艦炮的一個裝艦要素。長期以來,很多人認為多達幾十噸的后坐阻力對甲板基座的剛強度影響很大,甚至影響到艦炮的適裝性。但通過前文仿真分析可知,艦炮后坐阻力實際上是一個瞬時過程,炮架相當于剛度系數較高的彈性體,后坐阻力激勵的過程伴隨著炮架各網格單元的彈性應變能和動能的能量耗散,傳遞到甲板基座時的能量必然會有一定幅度的損耗。而后坐阻力傳遞到甲板基座的力,即炮架B面相配合的甲板基座表面對炮架B面提供的支反力,必然會比將炮架視為絕對剛體傳遞時的有所減小。同時,由于炮架B面、甲板基座安裝面的接觸面積更大,甲板基座受力后的應力應變會有顯著改善,遠較艦炮耳軸座受力后的狀態要好。
B面受到最大支反力的節點位于B面最大外圓部位并正對托架后部底部位置,節點編號8567,在z向上的支反力隨時間變化如圖17所示。該節點在受到突然施加的后坐阻力作用時,產生了突然增大然后波動、最后趨于穩定的向上的支反力,0.017 2 s時支反力最大到4.9 t,到0.15 s時支反力降到4.04 t,而以最大后坐阻力加載到同樣模型進行靜力學分析,最大支反力同樣出現在節點8 567,幅值為2.11 t,動態與靜態分析結果比值為1.91:1。在后坐阻力撤銷瞬時該節點的支反力突然換向,最大值達到負向3.54 t,之后在阻尼作用下逐漸衰減并在0.25 s時到0值。這一過程反映了B面最大支反力點的反力是一個動態、方向變化的事實。為進一步考察炮架B面支反力的整體情況,在環形B面上設定3條圓形路徑,半徑分別為1 280,1 200,1 120 mn,分別命名為path1,path2,path3路徑。參考最大支反力點出現最大力值的時刻,探求在0.017 2 s,0.153 6 s時刻3條路徑上的支反力情況。
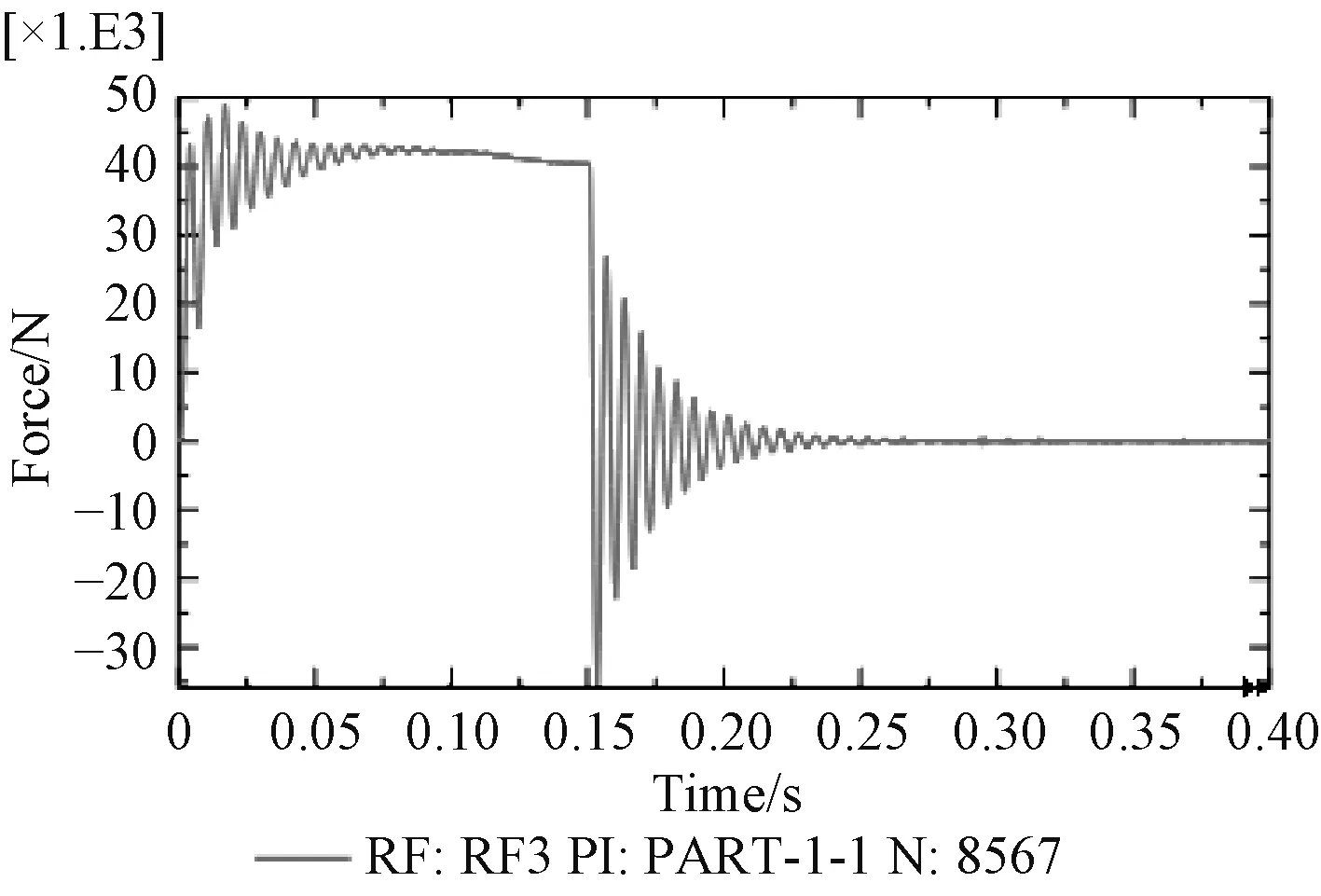
圖 17 最大支反力點的支反力時間曲線圖Fig. 17 Curve of reaction force of node 8567 vs. 17:50:03
圖18 ~圖23為在0.017 2 s、0.153 6 s兩特征時刻path1,path2,path3路徑上的垂向支反力、支反力幅值曲線圖。分析曲線圖可知,2個特征時刻各路徑上的垂向支反力方向剛好相反,絕對值不同;從環向看,路徑半徑越大,同一時刻垂向支反力越大;同一時刻同一路徑上各點的支反力大小不同,從模型坐標系來看,x軸正半軸與負半軸方向的垂向支反力剛好相反;垂向支反力4個最大值點剛好位于B面正對托架底部最前、最后部位;path2路徑可視為炮架與甲板基座連接螺栓分布圓的直徑,path2路徑上垂向支反力四個峰值均在1.5 t以下,作為靜不定結構,大部分點位上的支反力在0 t附近波動,僅僅考慮后坐阻力影響,不僅甲板基座結構設計能夠輕易實現較高剛度,連接螺栓同樣能夠達到極高安全系數。對于支反力幅值,包含了垂向、橫向、縱向分力,從絕對值來看支反力的幅值與垂向支反力絕對值相差很小,因此垂向支反力對于甲板基座剛強度起顯著作用,而橫向、縱向分力(最大值1.09 t)主要是對連接螺栓的剪切強度有影響。
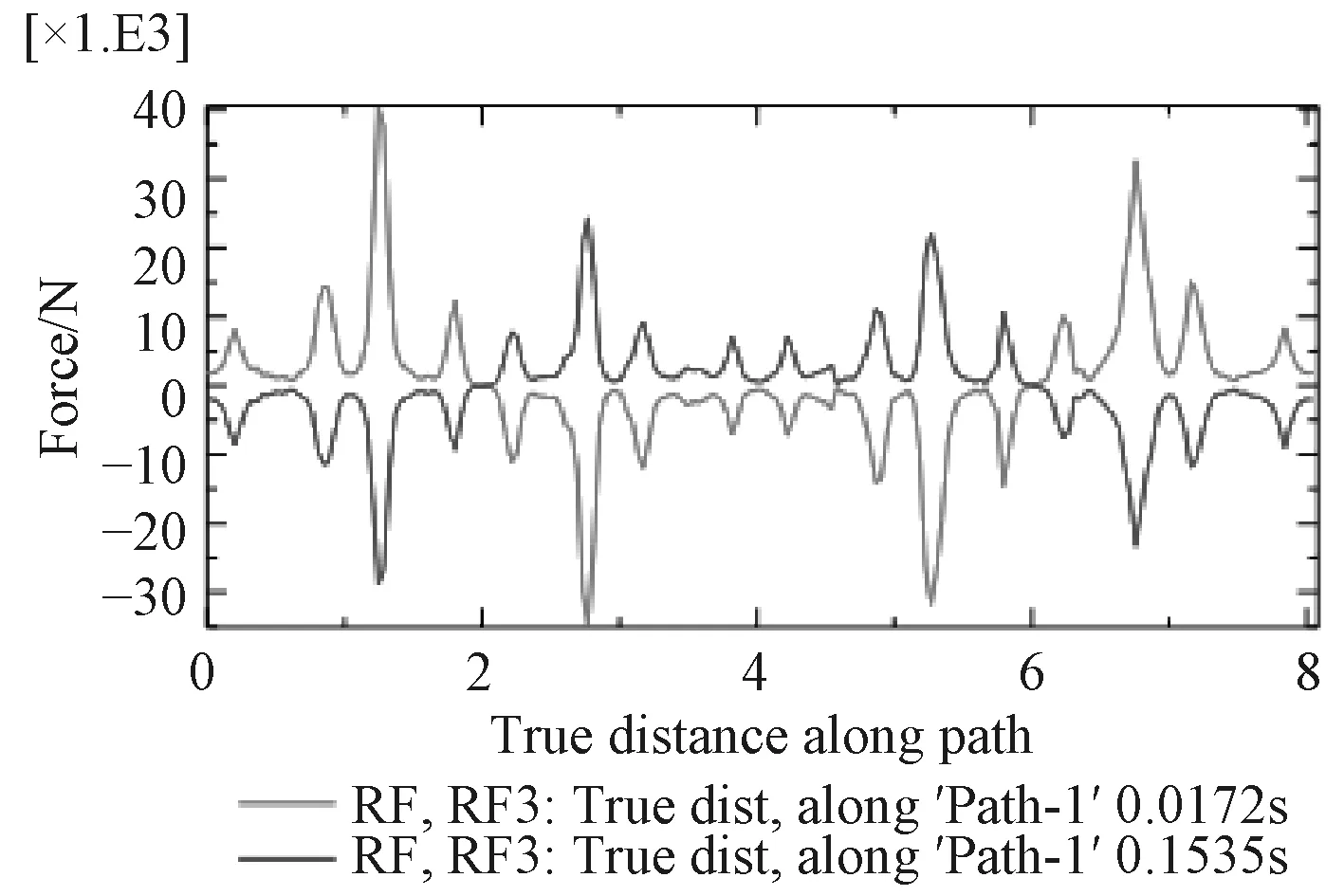
圖 18 兩特征時刻路徑1上的垂向支反力曲線Fig. 18 Curve of reaction force in z-direction vs. true distance along path1 under two typical time
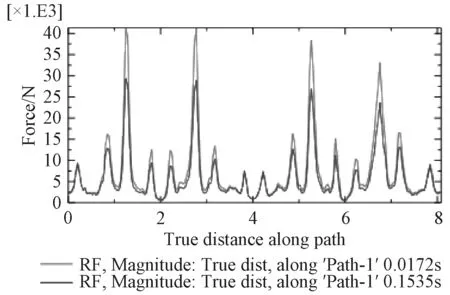
圖 19 兩特征時刻路徑1上的支反力幅值曲線Fig. 19 Curve of reaction force in magnitude vs. true distance along path1 under two typical time
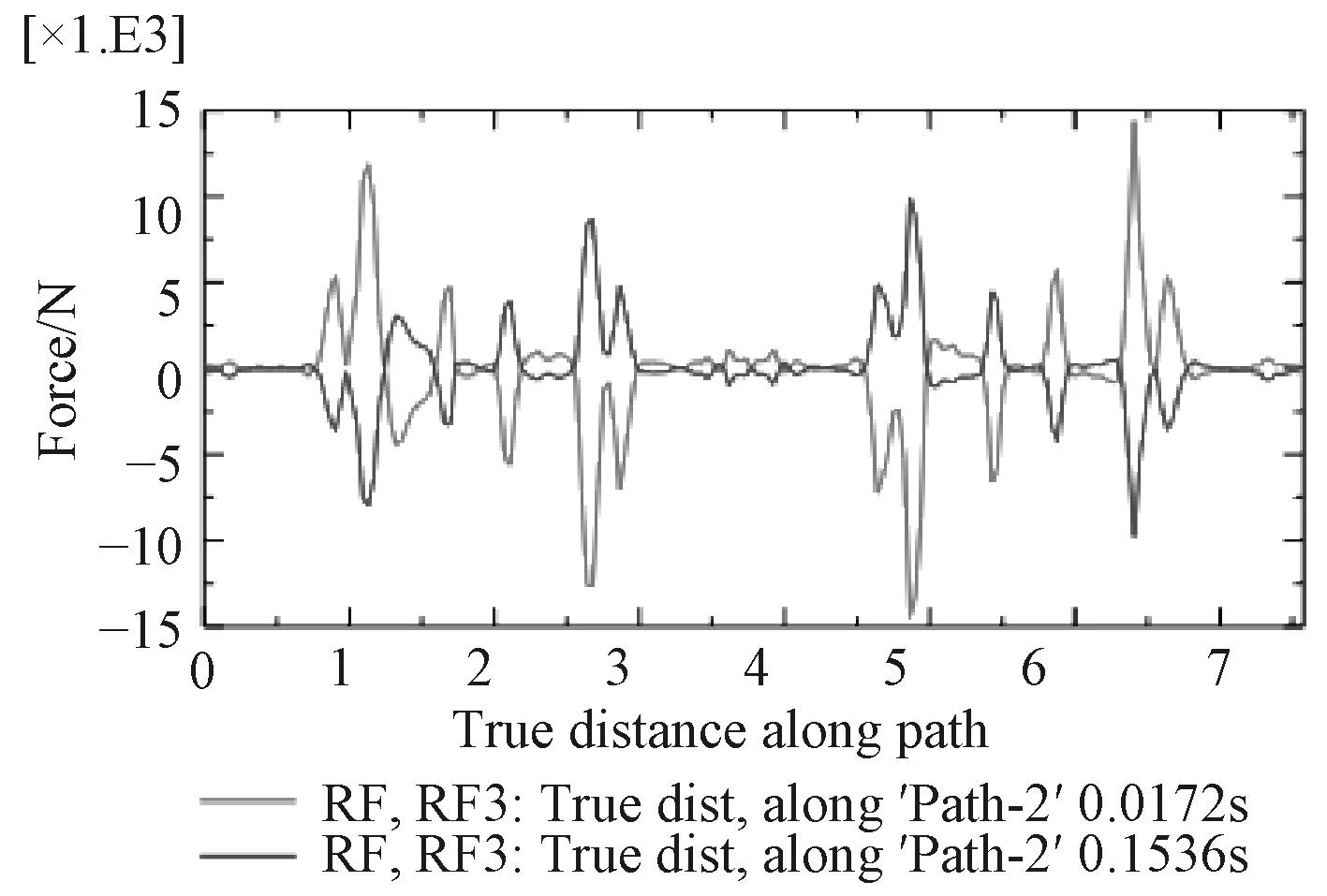
圖 20 兩特征時刻路徑2上的垂向支反力曲線Fig. 20 Curve of reaction force in z-direction vs. true distance along path2 under two typical time
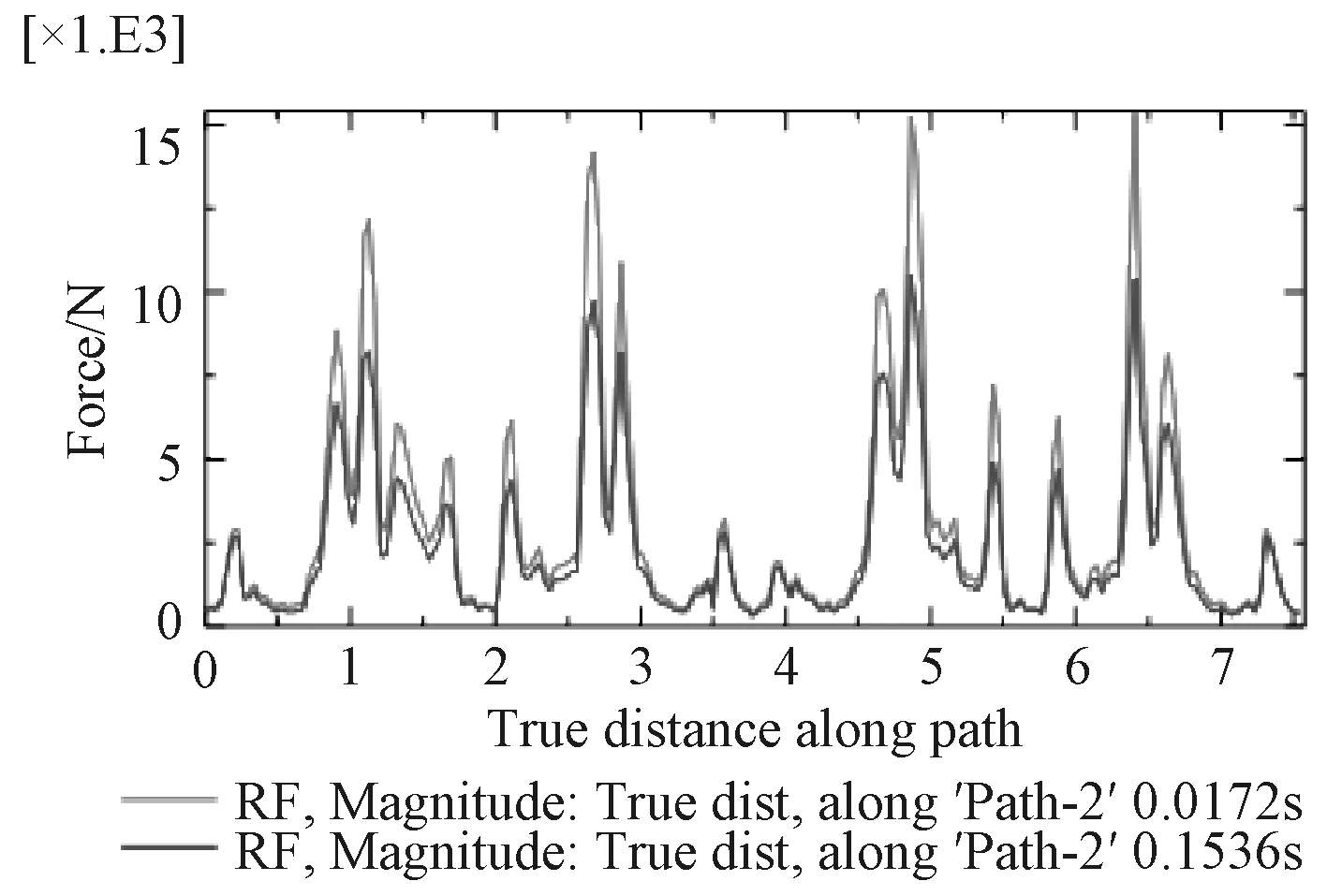
圖 21 兩特征時刻路徑2上的支反力幅值曲線Fig. 21 Curve of reaction force in magnitude vs. true distance along path2 under two typical time
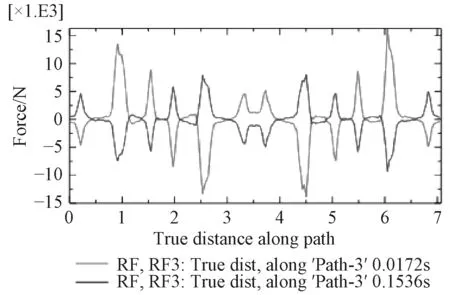
圖 22 兩特征時刻路徑3上的垂向支反力曲線Fig. 22 Curve of reaction force in z-direction vs. true distance along path3 under two typical time
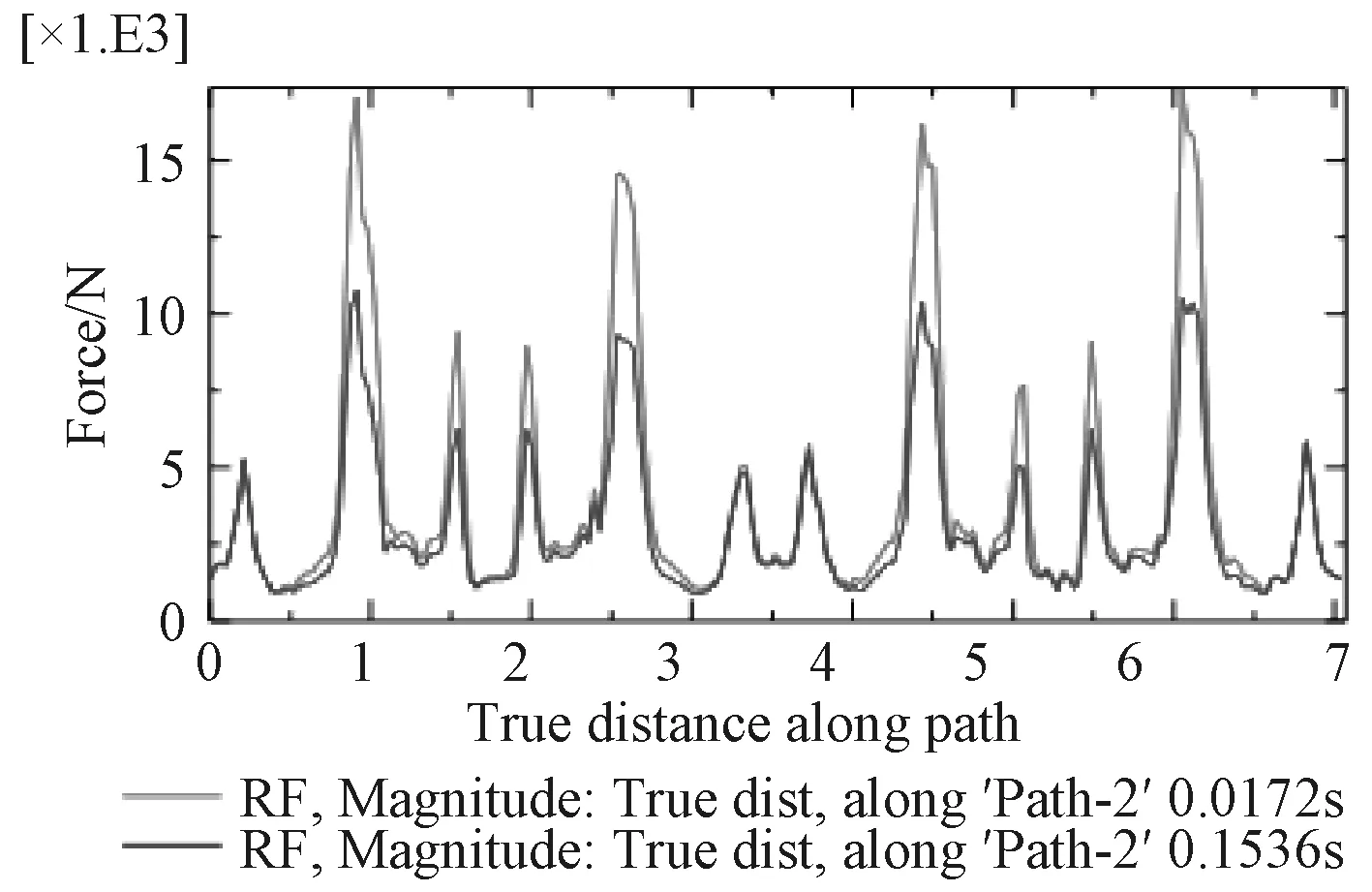
圖 23 兩特征時刻路徑3上的支反力幅值曲線Fig. 23 Curve of reaction force in magnitude vs. true distance along path3 under two typical time
5 結 語
本文同時對不同射角時后坐阻力的動態問題進行了分析。通過數值仿真,得出如下結論:
1)炮架結構設計確定后,應綜合考慮約束條件、振型激活總質量、各方向參與系數確定欲進行瞬時模態動態分析需要的固有頻率階數,確定哪階或哪幾階振型對炮架動態分析起決定性影響;
2)在后坐阻力激勵下,炮架的應力、變形、速度、加速度、支反力等都呈現出動態變化趨勢,其峰值應力、變形、支反力等較傳統靜力分析結果要高,炮架在外力激勵下的響應僅靠靜力計算不夠準確,實際安全系數偏小;
3)后坐阻力激勵的過程,實際上也是炮架自身單元彈性應變能、動能的不斷消耗過程,后坐阻力做功傳遞過程也是一個能量逐漸減小的過程,甲板基座安裝面單個螺栓連接部位不能簡單地以最大后坐阻力進行施加校核,安裝面所承受的垂向力沿圓周方向的分布值可以通過仿真得到,應重點關注安裝面正對托架底部前后結構對應部位的四處最大支反力,但單個幅值僅約為最大后坐阻力1/10;
4)炮架動態分析是設計趨勢,文中分析步驟對于艦炮動態分析具有指導作用。

