自主水下航行器固定舵對尾舵水動力的影響
嚴天宏,申洪彬,何 波,劉繼鑫,趙梓奎
(1. 中國計量大學 機電工程學院,浙江 杭州 310018;2. 中國海洋大學 信息科學與工程學院,山東 青島 266100)
0 引 言
隨著科學社會的快速發展,人口、環境和資源已經成為全球性問題,隨著資源的日漸減少,人類已經將目光投向海洋世界。自主水下航行器(Autonomous Underwater Vehicle,AUV)作為一種新型海洋環境移動監測平臺,具有靈活性高、自身作業能力強、下潛深度大、使用成本低及測量范圍大等特點,已逐步成為全球海洋探測領域技術研究的重點和熱點之一[1-3]。
水下航行器的姿態控制主要是通過尾舵的轉動提供升力。尾舵具有控制簡單,造價低,具有一定的穩定性等優點成為大多數水下航行器采用的控舵方式[4]。大多數的AUV設計都是將全動舵作為AUV的尾舵,但是考慮到水下環境復雜多變,本文在全動舵的正前方設計一個固定不動的舵以保證全動舵的安全,此固定舵的增加使AUV外形變復雜,必將會引起尾舵水動力性能的變化[5-7]。本文通過計算流體力學的方法對固定舵增加后會對水動力特性造成的影響,固定舵與全動舵之間的縫隙,鉸鏈力矩大小等關鍵的問題進行分析。
1 計算模型
1.1 數學模型
所有不可壓縮流體流動都遵循質量守恒定理和動量守恒定理,本文針對不可壓縮流體采用RANS方程,其中連續性和RANS方程[8-10]為:
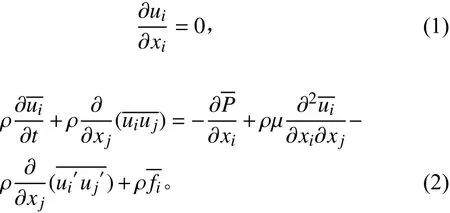
1.2 計算對象
本文選取的全動舵剖面形狀為一對對稱翼型。NACA-4數字系列翼型是美國NACA最早建立的一個低速翼型系列。這類翼型具有較高的最大升力系數和較低的最小阻力系數。由于NACA系列具有升力大、阻力小的特點而被廣泛使用。本文仿真實驗用的全動舵翼型為NACA0012,前2位“00”表示對稱翼型,后2位“12”表示厚度比的百分比。對于該種翼型的升力系數CL、 阻力系數CD、 扭矩系數CM公式如下:
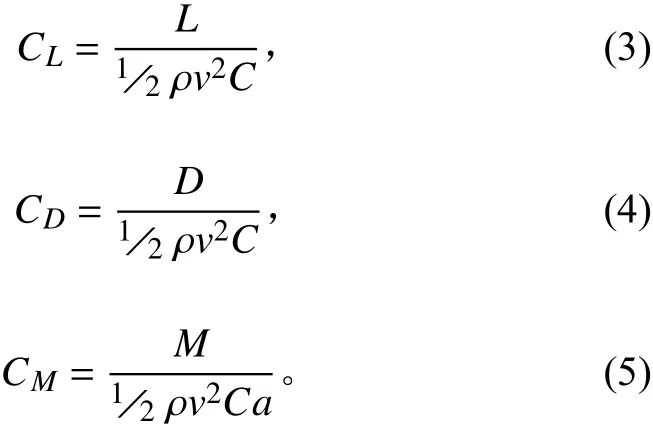
式中:L為翼型升力;D為翼型阻力;C為翼型弦長;M為舵片對軸扭矩;ρ為水的密度;v為水流速度;a為前緣至中心軸線距離。全動舵結構如圖1所示,其中根部弦長165 mm,翼端弦長125 mm,半展長197 mm。由于舵軸位置布置距離根部前點0.4倍弦長時具有最小鉸鏈力矩[11],故確定舵軸中心到根部翼型前點的垂直距離為67 mm。全動舵結構參數如圖1所示,固定舵結構參數如圖2所示,AUV尾舵空間布局實物圖如圖3所示。
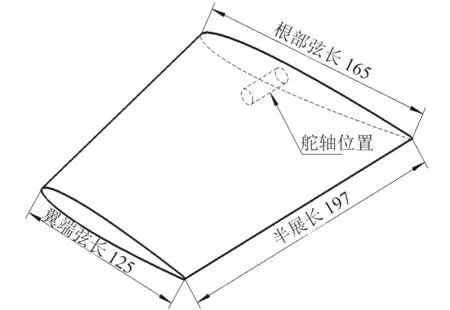
圖 1 全動舵結構參數圖Fig. 1 Structural parameters of the all-movable rudder
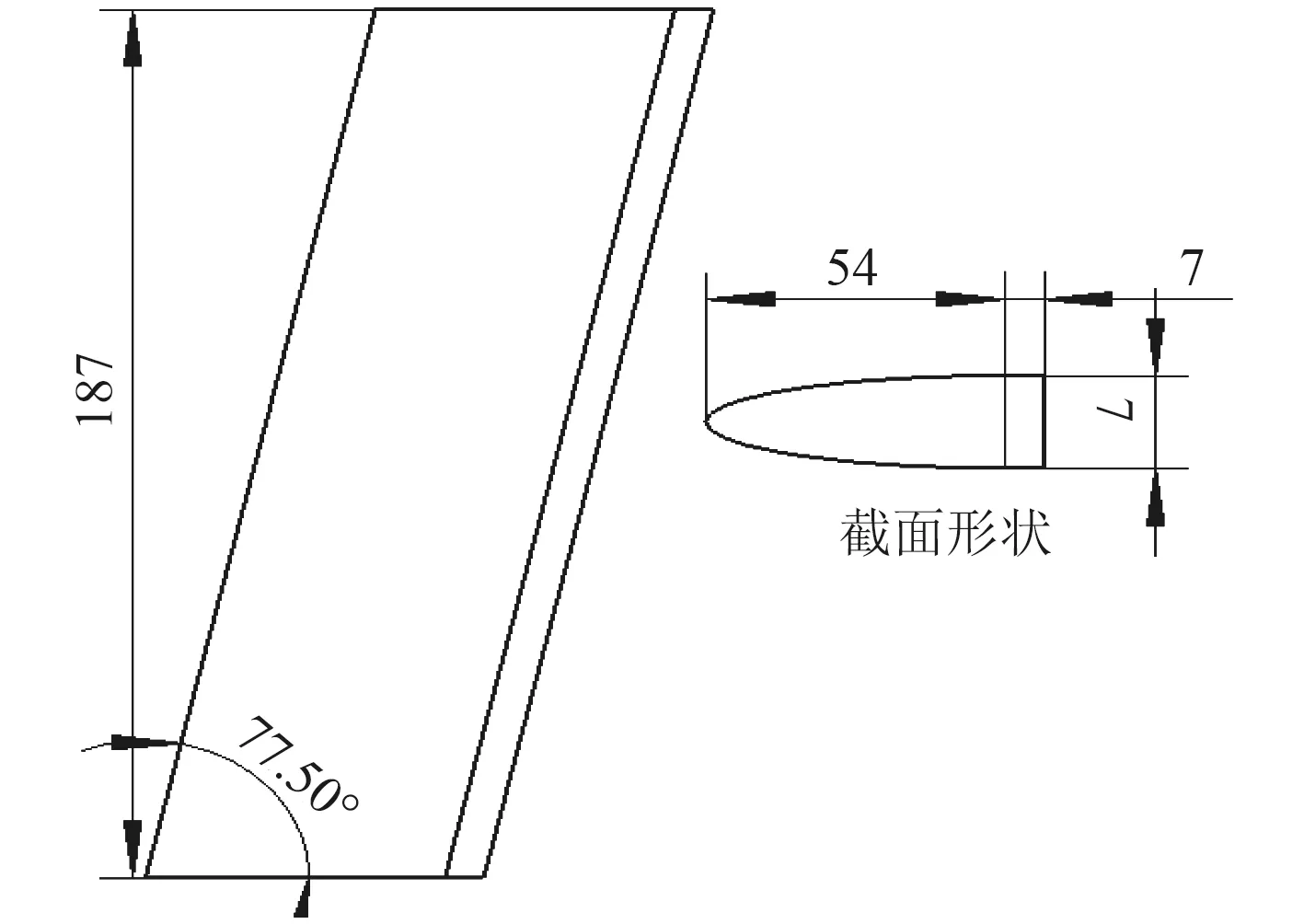
圖 2 固定舵結構參數圖Fig. 2 Structural parameters of the fixed rudder

圖 3 AUV實物圖Fig. 3 Appearance of the AUV
2 網格劃分與邊界條件
本文通過ICEM對尾舵部分進行網格劃分,選擇的流域為底面直徑400 mm,長度為750 mm的圓柱型流域。本文采用非結構化網格對尾舵模型進行網格劃分,表面的網格類型為三角形網格,體網格類型為Tetra/Mixed,AUV舵片的整體網格模型圖如圖4所示.
本文利用三維CFD方法模擬了不同來流速度,不同攻角尾舵的水動力特性。由于標準k-ε模型主要針對湍流發展比較充分的湍流流動建立的高雷諾數湍流計算模型,而RNG k-ε模型關注平均流動中的旋轉和旋流流動,比標準模型更具優越性[12-13],所以本文湍流方程選取RNGk-ε模型。進口條件設定為速度入口,出口條件設定為壓力出口,模型表面采用固定無滑移壁面設計。

圖 4 AUV舵片的整體網格模型圖Fig. 4 Overall mesh model of AUV rudder
3 全動舵與固定舵縫隙
本文通過改變固定舵與全動舵模型之間的縫隙大小,對不同縫隙不同攻角的尾舵在同一速度2 m/s狀態下進行網格劃分與水動力性能分析,得到的升力阻力與升阻比的關系如圖5~圖7所示。
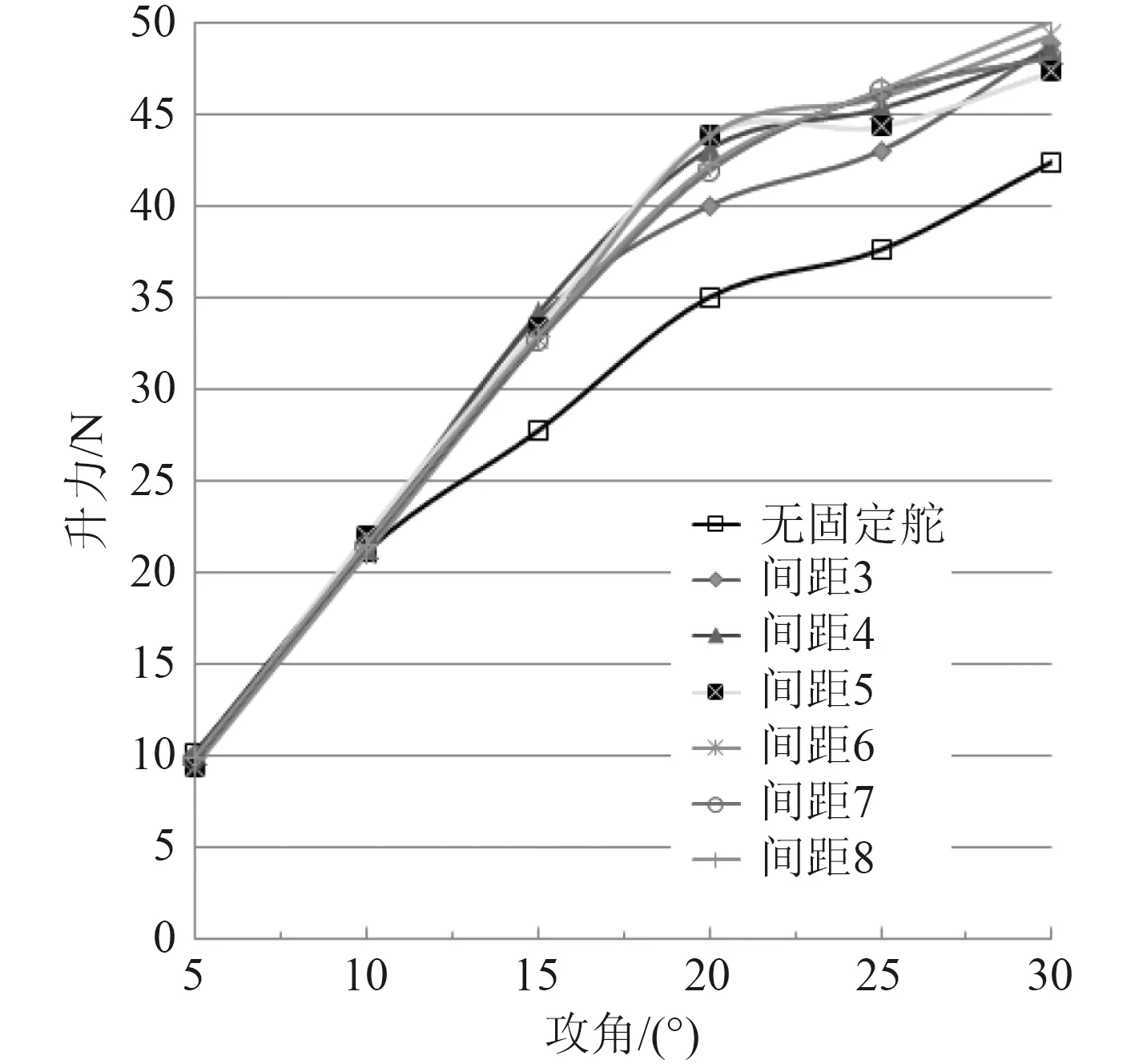
圖 5 不同攻角下的升力變化曲線Fig. 5 Lift curve at different angles of attack
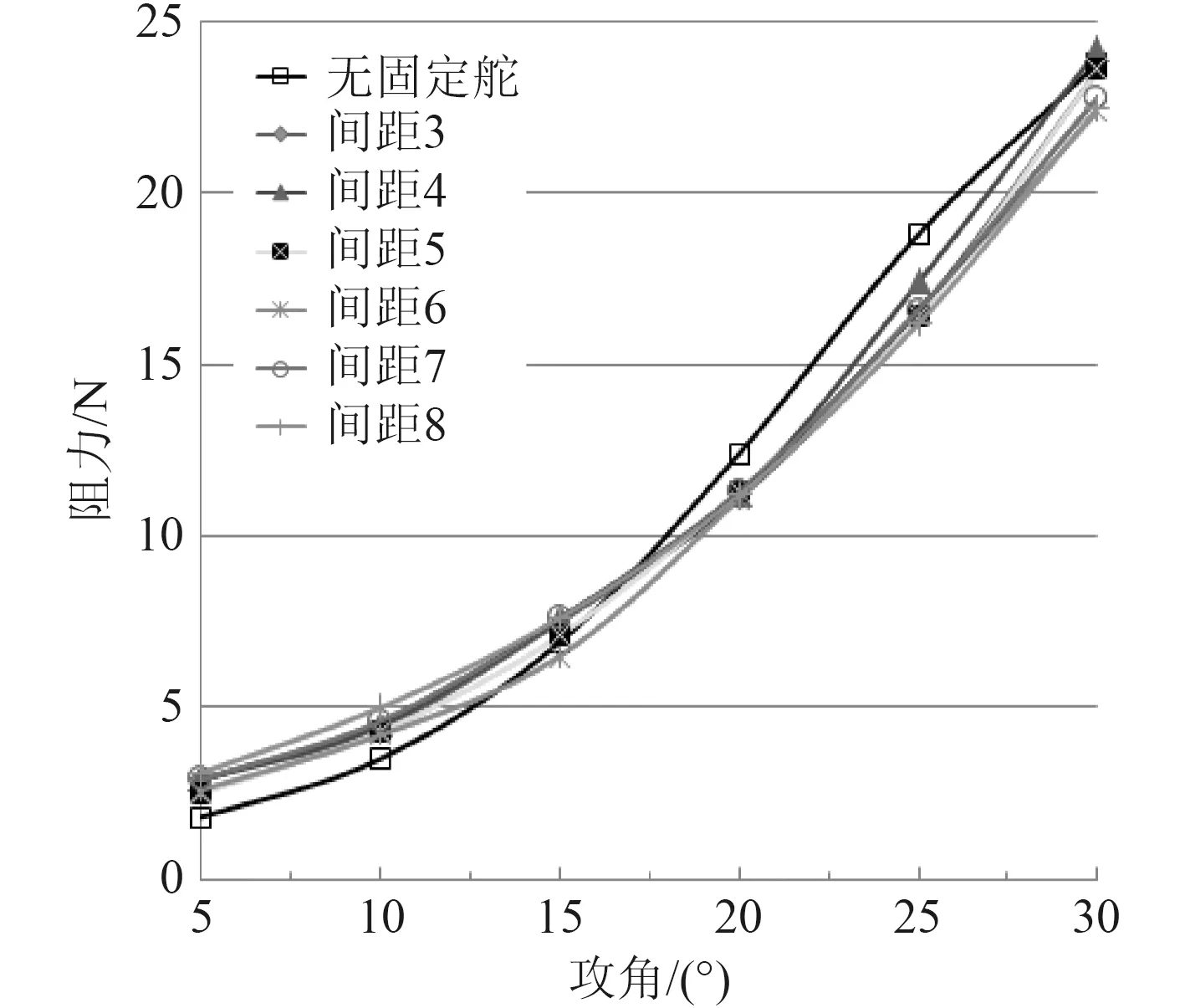
圖 6 不同攻角下的阻力變化曲線Fig. 6 Resistance curve at different angles of attack
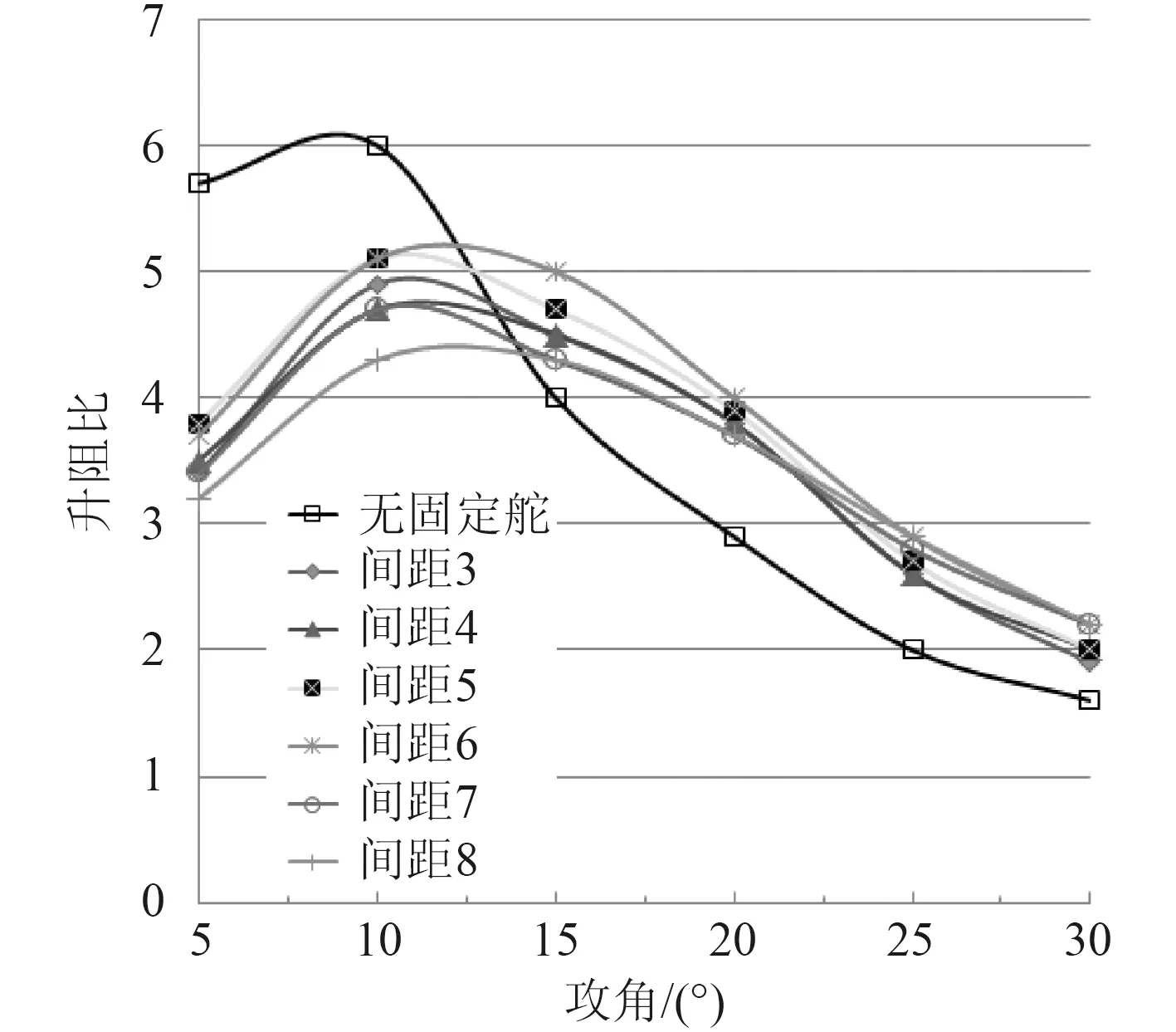
圖 7 不同攻角下的升阻比變化曲線Fig. 7 Lift-to-drag ratio curve at different angles of attack
圖7 為升阻比隨攻角的變化曲線。由圖可知,無固定舵片時尾舵能達到最大的升阻比,且最大的升阻比出現在攻角8°左右。結合圖5不同縫隙尾舵升力隨攻角變化曲線圖以及圖6不同縫隙尾舵阻力隨攻角變化曲線圖,可以看出攻角12°之前有無固定舵片及固定舵與全動舵片之間縫隙大小對尾舵的升力沒有產生明顯影響,但是固定舵的增加卻增加了舵片的阻力從而使安裝固定舵的尾舵升阻比在攻角12°之前小于單一全動舵的升阻比。故對于一些長期工作在低攻角狀態下的AUV或是對AUV升阻比要求較高的,不適于采用增加固定舵的方式保護全動舵。隨著攻角的增大,無固定舵片的全動舵升阻比在攻角12°之后開始小于有固定舵片的尾舵。攻角在15°之后無固定舵的尾舵阻力一直大于安裝固定舵的尾舵,升力曲線中也可以看出升力遠小于安裝固定舵的尾舵。
對于安裝固定舵的尾舵模型,分別取兩舵間距3,4,5,6,7,8作為研究對象,分析出6種間距模型在不同狀態的升阻比。可以看出兩舵間距對舵升阻比的影響較明顯,而且兩舵間距為6 mm的舵片模型升阻比一直高于其他間距的升阻比。所以對于安裝固定舵保護全動舵的AUV建議將固定舵與全動舵之間的間隙保持6 mm。
圖8為單一全動舵壓強分布云圖,圖9為兩舵間距6 mm時壓強分布圖,兩圖都是全動舵攻角為15°時的壓強云圖。從圖8可以看出舵片前緣迎流面與背流面兩側的壓力分布相反且壓強值較大,而到了尾舵后緣背流面出現了較大壓強值說明尾舵后緣出現繞流現象。

圖 8 全動舵壓強分布云圖Fig. 8 Pressure distribution of all-movable rudder
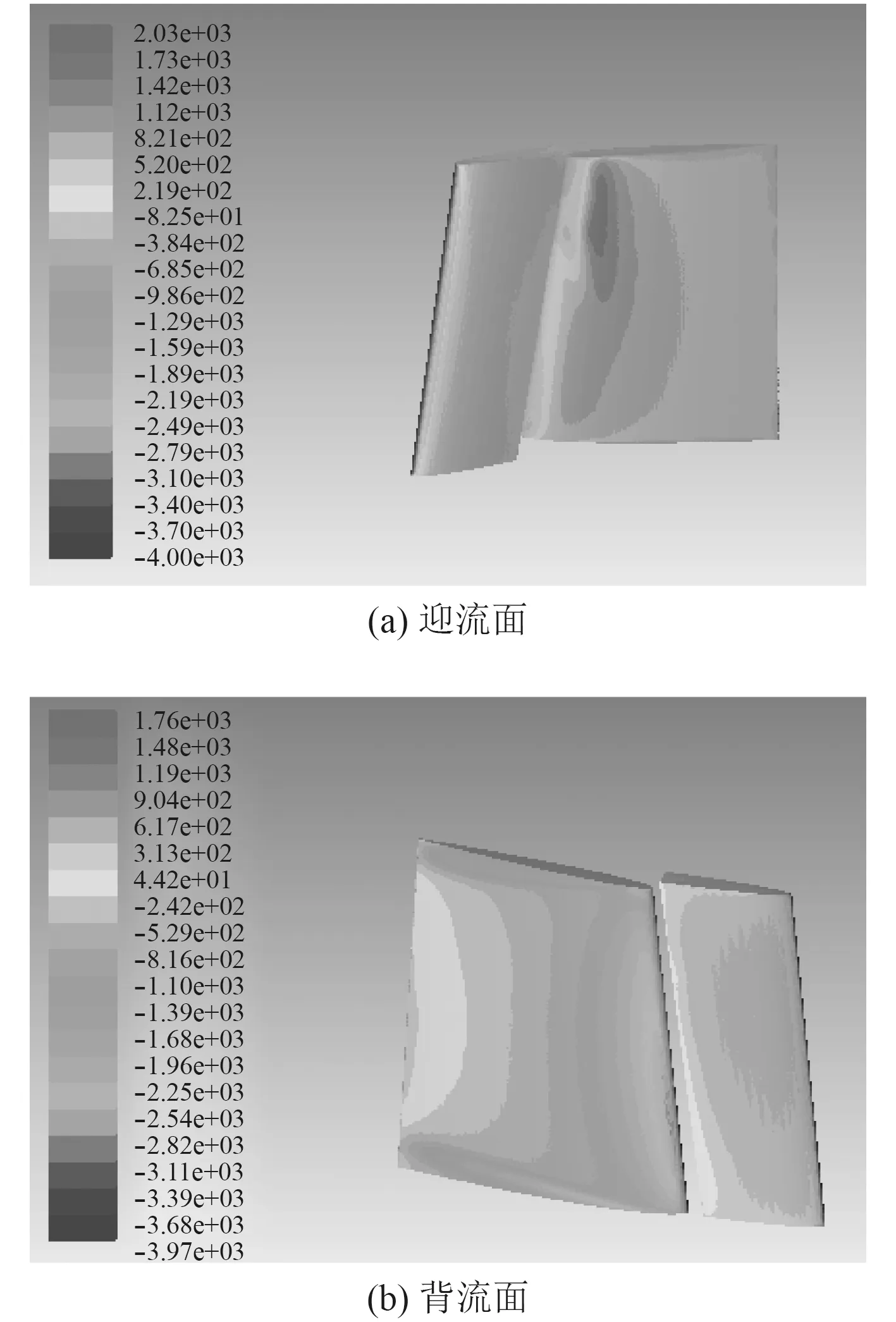
圖 9 兩舵間距6 mm時壓力分布云圖Fig. 9 Pressure distribution at a distance of 6 mm between the two rudders
綜合以上可知,單一全動舵的最大壓強值出現在舵片前緣而安裝固定舵片的模型在固定舵的前緣出現了最大壓強值而不是全動舵的前緣。固定舵前緣的大壓力導致了大阻力的產生。安裝有固定舵片的尾舵迎流面壓強較大,而且固定舵片的迎流面壓強也大于背流面,說明此時的固定舵片也可以提供一部分升力。
為了確認固定舵片的增加對整個系統的影響是否和速度有關,本文對舵片攻角20°的2種模型(單一全動舵模型和安裝固定舵且固定舵與全動舵間距為6 mm的模型)在不同速度下進行了對比分析得到數據如表1所示。
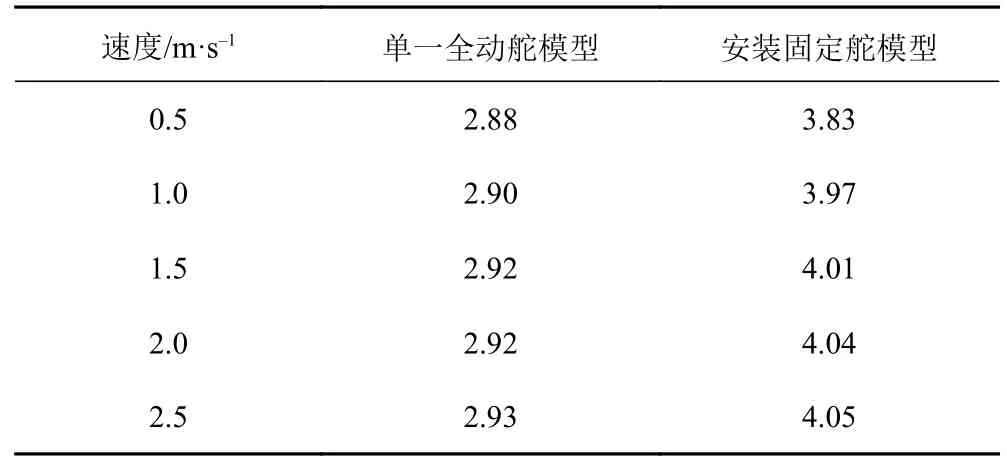
表 1 兩種舵片模型在不同速度下的升阻比對比表Tab. 1 Comparison of lift-drag ratio of two rudder blade models at different speeds
可以看出,單一全動舵的升阻比隨著速度升高略有升高,安裝固定舵片的升阻比也隨著速度的升高略有升高且始終大于單一全動舵升阻比。綜上可和,整個系統的升阻比只和是否增加固定舵片以及全動舵的攻角大小有關,故固定舵片引起的升阻比升高和速度無關。
4 鉸鏈力矩分析
鉸鏈力矩是指流過片的流體對舵軸形成的力矩。執行機構一般是通過機械傳遞控制舵片的偏轉,為了使舵面偏轉到需要的位置,必須克服作用在舵軸上的鉸鏈力矩。鉸鏈力矩越大則舵的偏轉速度越小,航行器對控制的反應越慢[14]。為了研究保護舵的增加對鉸鏈力矩的影響,本文選取無保護舵模型和間距為6 mm的兩舵模型進行對比分析,結果如圖10所示。
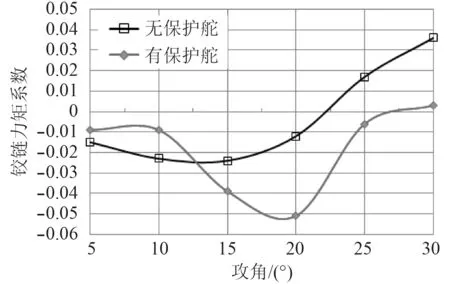
圖 10 不同攻角下的鉸鏈力矩系數變化曲線圖Fig. 10 Hinge moment coefficient curve under different angles of attack
可以看出,單一全動舵的鉸鏈力矩系數變化較平穩,約22°以后出現隨攻角快速增大現象。有保護舵的模型鉸鏈力矩系數約在12°~25°之間大于無保護舵模型,且變化率較為明顯。最大鉸鏈力矩系數出現在20°左右。綜上所述,保護舵片的增加增大了系統的鉸鏈力矩且在15°~25°之間變化較大。
5 結 語
本文運用CFD數值計算方法對固定舵片與全動舵片的不同安裝縫隙進行研究,分析了在2 m/s的速度下固定舵片與全動舵片之間的縫隙大小對整體升力、阻力以及升阻比的影響,進而分析出固定舵片與全動舵的最佳安裝縫隙,為AUV設計保護舵片提供一定的參考。通過仿真數據比對兩舵片的不同安裝縫隙以及不同的攻角得出以下結論:
1)當全動舵片攻角小于12°時,固定舵片的增加雖沒有對全動舵的升力產生影響卻導致全動舵的阻力增加,故安裝固定舵片系統在全動舵攻角小于12°時會降低系統整體性能。
2)當全動舵片攻角大于12°時,安裝固定舵片的模型升力開始大于單一全動舵模型,且在15°之后阻力開始小于單一全動舵,使得整個系統的升阻比大幅提升,所以安裝固定舵片系統在全動舵攻角大于12°時有利于提高系統性能。
3)對于需安裝固定舵片保護全動舵的AUV建議將兩舵片的縫隙定為6 mm,6 mm的間距使得大部分攻角的升阻比都大于其他間距。
4)保護舵片的增加增大了系統的鉸鏈力矩,最大鉸鏈力矩出現在20°左右。

