面向AUV水下移動對接的實時路徑規劃方法

時常鳴，劉開周，趙 洋，趙寶德

(1. 中國科學院沈陽自動化研究所 機器人學國家重點實驗室，遼寧 沈陽 110016；2. 中國科學院機器人與智能制造創新研究院，遼寧 沈陽 110016；3. 中國科學院大學，北京 100049)

0 引 言

自主水下機器人（Autonomous Underwater Vehicle，AUV）是探索海洋空間的有力工具之一，在海洋科學考察和海底資源勘測等領域獲得廣泛應用。利用水下對接平臺對AUV進行自主對接，可以實現AUV能源補充、數據上傳和使命下載，從而增強AUV的續航力與作業能力，降低AUV的應用成本。而AUV與移動對接平臺之間的實時路徑規劃技術，是AUV與水下對接平臺自主對接的使能技術之一。

Ken T等[1-2]提出一種基于TSK模糊理論的AUV對接控制方法，利用AUV與水下固定式對接平臺之間的橫向誤差、縱向誤差、AUV的期望縱向速度和艏向角建立相應的模糊策略，通過仿真實驗和實際實驗結果證明，該方法可使AUV在沒有障礙物和海流未知的情況下回收到水下固定對接平臺內；Jantapremjit P等[3-4]將對接階段分為2個階段，利用切換加權系數的人工矢量場法，使AUV沿著水下固定對接平臺的中軸線運動，達到對接所需方向和位置最終實現AUV的安全對接；李曄和姜言清等[5-6]提出一種基于3次B樣條和遺傳算法的AUV小范圍靜態路徑規劃方法，該方法滿足AUV對接過程中所需的終端約束和運動約束。上述方法都是AUV與水下固定對接平臺之間的路徑規劃方法，存在容易陷入局部極值或運算復雜規劃時間長等缺點，無法滿足環境未知的情況下，AUV與水下移動平臺對接的實時性需求。

本文針對復雜動態環境下AUV與水下移動平臺對接的實時性和終端姿態需求，研究了一種基于混合整數線性規劃[7]（Mixed Integer Linear Programming，MILP）的AUV與水下移動平臺對接路徑規劃方法，根據對接階段的需求設計了不同的目標優化函數，實現了移動對接目標函數建模，對障礙物約束和AUV本體約束進行了相應的線性化，建立起由線性化約束和目標函數組成的線性規劃模型，在相對速度坐標系下實現對AUV加速度的優化，實時規劃出AUV相應的縱向速度和艏向角，并充分考慮AUV實際的動力學模型，最終在AUV與水下移動平臺之間得到滿足所有約束且目標函數最優的實時優化路徑，利用仿真實驗驗證該方法的有效性。

1 問題描述

本文將對接過程分為2個階段：歸航階段和終端導引階段[8-9]。第1階段，AUV通過超短基線等傳感器快速到達對接平臺前方一定距離位置[10]；第2階段，AUV通過高精度傳感器（聲、光、磁等）進行精確導航定位，根據當前的位置和艏向，以及水下對接平臺的位置及艏向，最終以期望的航向姿態完成欠驅動AUV與水下移動對接平臺之間的精確移動對接。

MILP是在線性規劃（Linear Programming，LP）的基礎上發展而來的一種優化方法，它融入了整數變量，可以解決具有復雜邏輯關系的實數-整數混合優化問題。為了利用MILP優化方法更好地解決AUV與水下移動平臺之間的實時優化路徑規劃問題，在此，進行相關假設和簡化：

圖 1 AUV與水下移動平臺對接過程示意圖Fig. 1 Diagram of docking process between AUV and underwater mobile platform

1）設AUV、障礙物和水下對接平臺的當前時刻的相對位置和相對速度已知，且下一時刻的相對位置和相對速度未知；

2）設在極小時間周期內，障礙物和水下移動平臺的速度保持不變；

3）設對接階段水下對接平臺航行速度小于AUV的速度；

4）設水下對接平臺沿著水下移動平臺的中軸線方向移動。

2 約束建模

2.1 障礙物約束的線性化

如圖2所示，設E-ξη為固定坐標系，點A表示AUV,點O表示為障礙物的圓心；VA和VO分別表示為AUV和障礙物的當前速度矢量，VAO表示為AUV和障礙物之間的相對速度矢量,VAO=VA-VO；LAO表示為AUV和障礙物之間的相對位置矢量； γAO表示為之間的夾角，以VAO在LAO右側為正，取值范圍為 (-π,π]， 同理，與邊界AM或AN的夾角，表示為單位時間內γAOC的改變量。

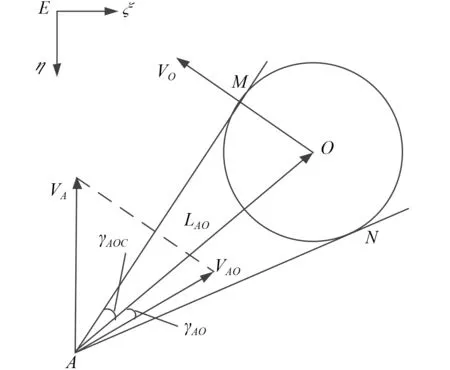
圖 2 AUV-障礙物示意圖Fig. 2 Diagram of AUV-obstacle

為了使AUV可以避開多個障礙物，障礙物約束的線性化模型可以寫成：

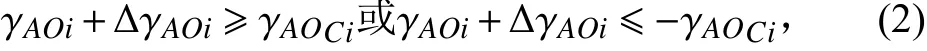
其中：i=1,2,...N。

為了解決AUV避開障礙物時的轉向問題，可以將式(2)寫成：

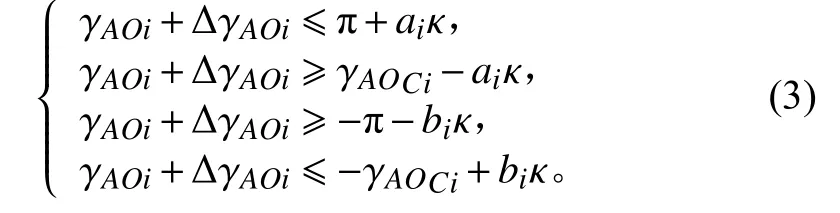
其 中ai+bi=1，ai和bi都 為 二 進 制 變 量 ，κ 為 遠 大 于 不等式左側的正實數。

當ai=0,bi=1時，式（3）中前2個等式成立，表示AUV從障礙物的右側避開障礙物；

當ai=1,bi=0時，式（3）中后2個等式成立，表示AUV從障礙物的左側避開障礙物。

2.2 AUV本體約束

考慮 AUV動力學模型，由于螺旋槳的轉速極限約束，欠驅動AUV航速不會太大，由AUV操縱性知識可知，過低的航速會導致方向舵失效。假設在單個采樣周期Δt內自主水下機器人的速度和加速度保持不變，且滿足約束：

聯立式（4）和式（5）得加速度分量約束如下：

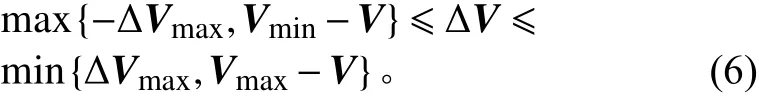
3 目標函數建模

目標函數是根據AUV與水下移動平臺對接的任務需求來確定的。在AUV回收的第1階段，目的是盡快縮短AUV與水下移動平臺的距離，并快速到達大致預定位置，這里與其他AUV路徑規劃問題類似，只需要解決目標點的到達問題；第2階段，目的是AUV以期望的航向姿態盡快與水下移動平臺完成對接，這里與其他AUV路徑規劃問題不同的是，不僅需要解決目標點的到達問題，還要保證AUV是以期望方向到達目標點。

3.1 距離收斂

為了使AUV與水下移動平臺之間的距離越來越近（見圖3），即，則可以寫作：

其中，分別表示為AUV與水下移動對接平臺之間的相對位置矢量和相對速度矢量，表示在單個采樣周期內的變化量。

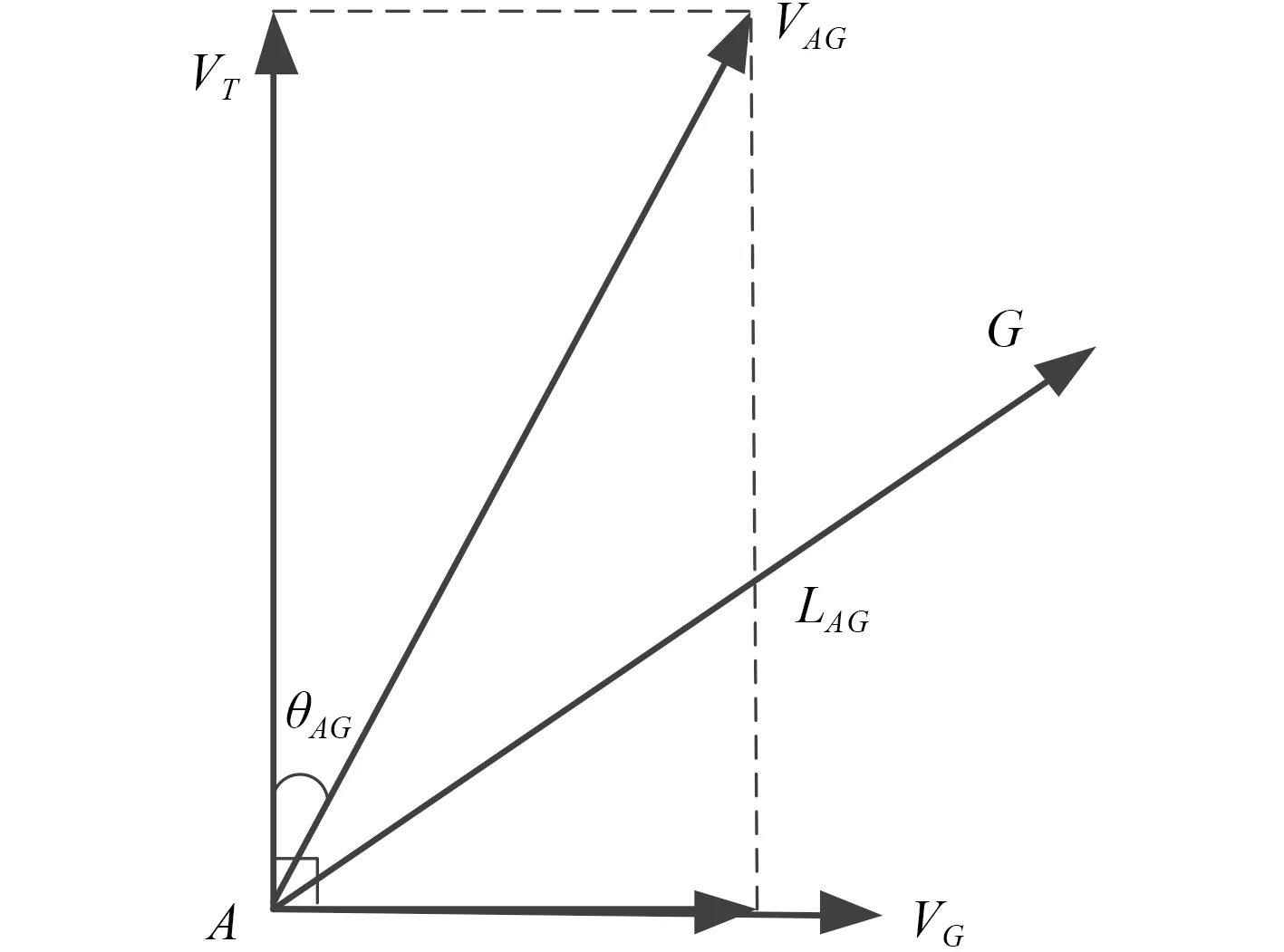
圖 3 相對速度的速度分解Fig. 3 Velocity decomposition of relative velocity

為了方便計算，式（7）寫作：

其中，j表示維數。

3.2 時間最優

為了盡快縮短AUV與水下移動對接平臺之間的相對距離，AUV與目標的相對速度VAG在沿著相對位置矢量LAG上的分量應該最大，即

經過線性化[11]以及為了與距離收斂目標函數式（8）相對應，式（9）最終為：

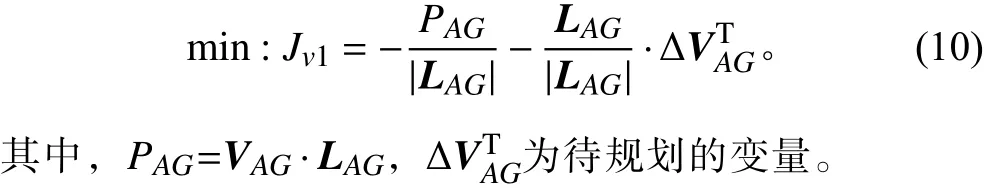
3.3 姿態最優

為了使AUV以期望的航向姿態與水下移動平臺完成對接，AUV與目標的相對速度VAG沿垂直于水下移動平臺移動速度VG的分量應該最大，即

設n為VT的 單 位 向 量 ， 為 了 使的 同一側，則n可表示為：

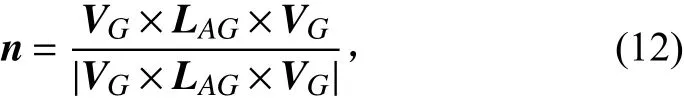
令

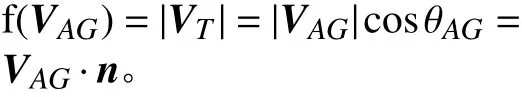
根據泰勒公式可知：

其 中 ， ?f=n表 示 函 數 f(VAG) 的 梯 度 ，o(||ΔVAG||)表 示泰勒余項。

忽略高階項，以及為了與距離收斂目標函數式（8）相對應，式（11）最終為，

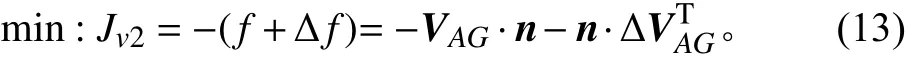
3.4 移動對接目標函數建模

在AUV與水下移動平臺對接的第1階段，只需要考慮目標點到達問題；在第2階段，不僅需要考慮目標點達到問題，還要保證AUV是以期望方向到達目標點。同時根據子目標函數的分析，可得總的目標函數：

其中，i=1,2,…M,表示維數，這里取M=2，表示二維平面 ， ωi,ωv1,ωv2≥0 為權值 ， φAG為VG與LAG之間 的 夾角，為開始進行AUV與水下移動平臺對接的第二階段的最小距離， φmin為AUV與水下移動平臺最終對接時允許的最小姿態偏差。

4 算法流程

AUV與水下移動對接平臺的精確對接系統的實時路徑規劃流程圖如圖4所示。具體的算法流程如下：

1）通過傳感器數據獲得水下移動平臺和障礙物的位置信息和速度信息；

2）對傳感器約束和本體約束進行線性化，獲得相應模型；

3）根據規劃策略公式（14）設計相應的目標函數；

4）利用MILP規劃器實現對AUV加速度的優化，并得到 期望的速度ud和 航 向ψd：

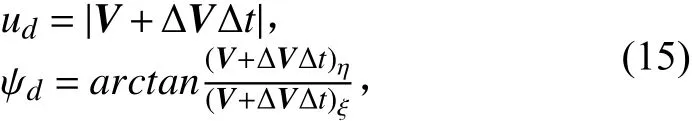
其中， (V+ΔVΔt)η， (V+ΔVΔt)ξ分別為速度矢量在η，ξ方向上的分項量；

5）將航行控制器作用于AUV的實際動力學模型上，得到實際的速度u和 航向 ψ；

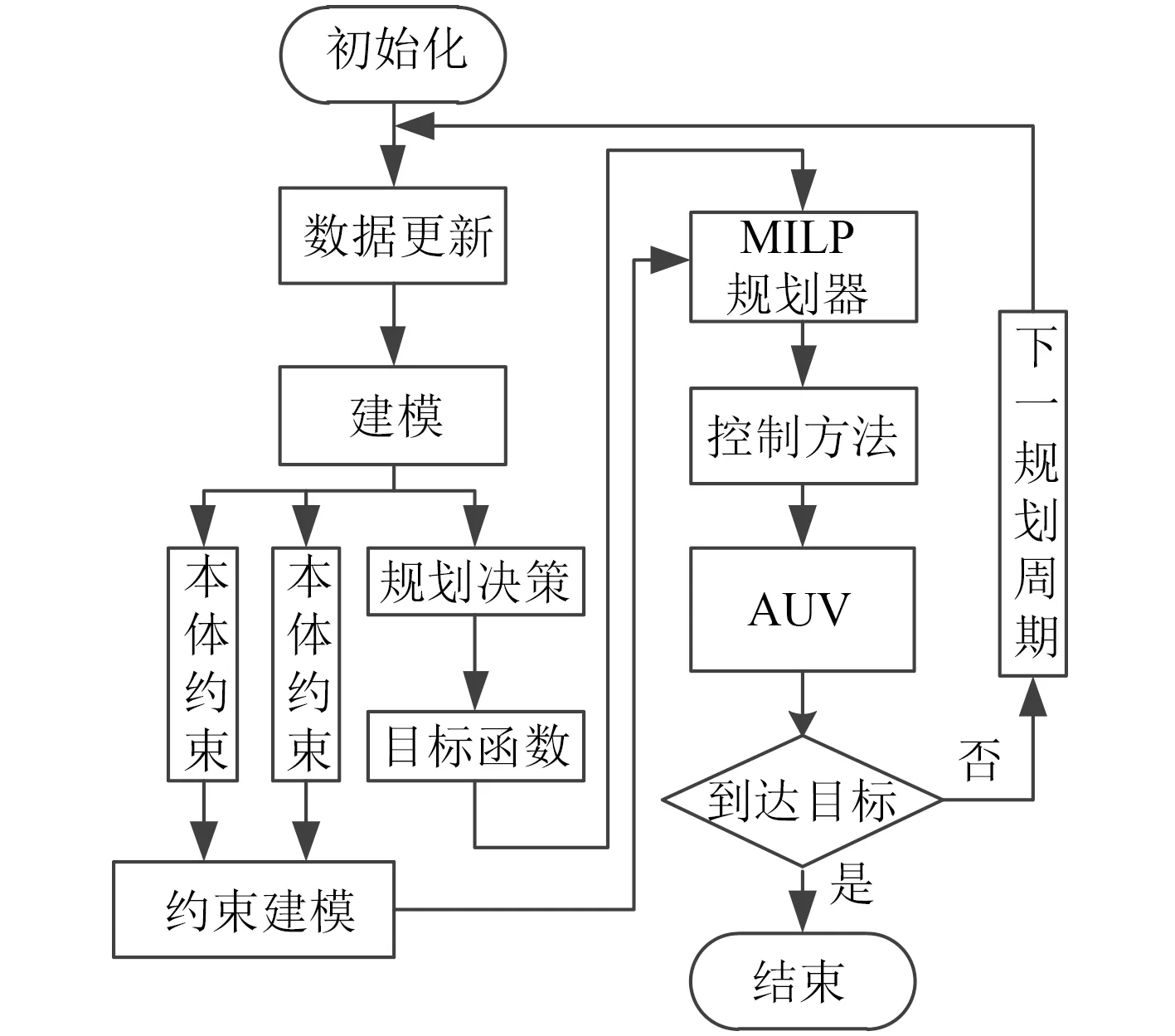
圖 4 算法流程圖Fig. 4 Flow diagram of algorithm

6）根據實際的速度u和航向 ψ ，得到下一時刻AUV的位置，即

7）判斷AUV是否到達水下移動對接平臺位置，如果到達，則規劃算法結束，否則返回步驟2進行下一周期規劃。

5 仿真實驗

仿真實驗在Matlab R2015b下進行，采用PID控制器對某型AUV進行航行控制。MILP的規劃周期Δt=1s，開始進行AUV與水下移動平臺對接的第二階段的最小距離dmin=50m， 允許的最小姿態偏差 φmin=15°，表1給出了仿真實驗中AUV、障礙物和水下移動對接平臺的位置信息和速度信息等信息。

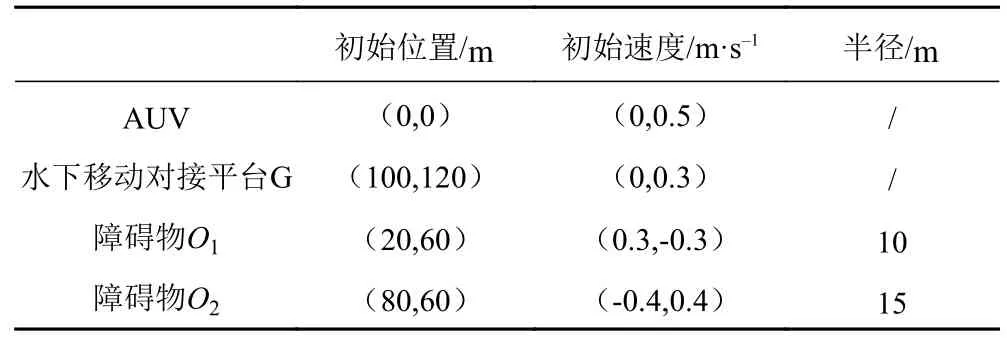
表 1 仿真實驗初始值Tab. 1 Initial value of simulation experiment

根據仿真結果可知，MILP單步規劃時間約為0.18 s，可以滿足AUV與水下移動平臺之間路徑規劃的實時性需求。由圖5可知，AUV可以有效避開障礙物O1和障礙物O2，AUV在位置 (83.20,103.01)處進入AUV與水下移動平臺對接的第2階段，最終在(100.00,166.50)處完成對接任務。由圖6可知，AUV的縱向速度越來越大，在60 s左右達到Vmax，AUV在114 s左右進入AUV與水下移動平臺對接的第2階段，在160 s左右完成對接任務。由圖7可知，AUV最終以航向角偏差φAG≈3°的航向姿態與水下移動平臺完成對接，滿足對接要求。

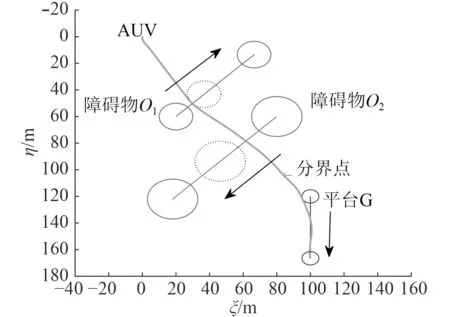
圖 5 實時規劃路徑圖Fig. 5 Real-time path planning map

圖 6 AUV速度曲線Fig. 6 The velocity curve of AUV

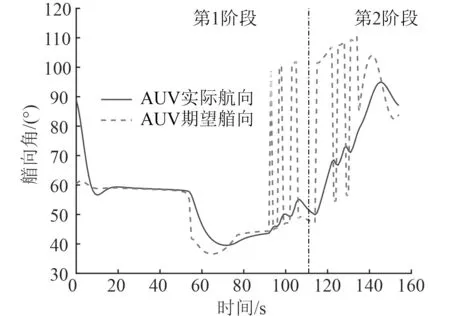
圖 7 AUV航向曲線Fig. 7 The heading curve of AUV

6 結 語

以往的大多數路徑規劃算法只考慮目標點的到達問題，沒有考慮AUV到達目標點的姿態需求。本文針對復雜動態環境下AUV與水下移動對接平臺的實時性和終端姿態需求，提出一種基于MILP的實時路徑規劃方法。充分考慮了障礙物約束、AUV本體約束，根據多個對接階段的需求設計了距離收斂、時間最優和姿態最優等不同的目標優化函數，建立了移動對接目標函數，形成相應的多約束線性規劃模型，實現對AUV加速度優化。仿真結果表明，該算法能滿足AUV與水下移動對接平臺的實時性和終端姿態需求。

AUV的期望航向在路徑規劃的后半程存在劇烈變化，分析可知，這是由于AUV參數的設計不太恰當導致的，需要進一步改進。下一步需要考慮海流對AUV和水下移動對接平臺運動的影響，以便更好地滿足實際工程需要。