基于灰色-BP網絡以及馬爾科夫算法的天然氣年消費量預測

劉卓良 彭喜亮 潘振 劉培勝

摘? ? ? 要： 采用灰色關聯度分析法對我國天然氣年消費量的影響因素進行篩選，將灰色關聯度數值較大的影響因素作為BP（Back-propagation）神經網絡預測的輸入向量，進而建立灰色-BP神經網絡模型對我國年天然氣年消費量進行預測，利用天然氣消費量的預測值與實際值的誤差得出適用于本次預測的馬爾科夫矩陣，再采用馬爾科夫矩陣對進一步的天然氣消費量預測數值進行誤差修正，進而得到更為精準的預測結果。以往數據表明，我國天然氣年消費量的主要影響因素為天然氣產量及進口量、煤炭、石油以及其他能源消費量。通過灰? ? 色-BP模型預測得出的天然氣年消費量數值與天然氣的實際年消費量數值進行比較，預測結果顯示灰色-BP神經網絡模型適用于對我國天然氣年消費量的預測，通過得到的馬爾科夫矩陣對進一步的預測結果進行修正，經修正后誤差有減小趨勢，說明馬爾科夫法可有效減小預測誤差。

關? 鍵? 詞：天然氣年消費量;預測模型;灰色關聯度;BP神經網絡;馬爾科夫法

中圖分類號：TE 820? ? ? ? 文獻標識碼： A? ? ? ?文章編號： 1671-0460（2020）09-1977-06

Abstract： The factors affecting the annual consumption of natural gas in China were screened by the grey correlation analysis method. The influence factors of the large grey relational value were used as the input vector of the BP （Back-propagation） neural network prediction， and the grey -BP neural network model was established to predict China's annual natural gas consumption. The error of the predicted value of gas consumption and the actual value was used to obtain the Markoff matrix which was suitable for this prediction， and then the Markoff matrix was used to further correct the prediction value of natural gas consumption， and then a more accurate prediction result was obtained. Previous data showed that the main factors affecting the annual consumption of natural gas were natural gas output and import quantum， the consumption of coal， oil and other energy. The annual consumption value of natural gas predicted by the grey-BP model was compared with the actual annual consumption of natural gas. The prediction results showed that the grey -BP neural network model was suitable for the forecast of annual consumption of natural gas in China. The results of the further prediction were amended by the Markoff matrix， and the post error had a decreasing trend， showing that Marco's method can effectively reduce the prediction error.

Key words： Annual consumption of natural gas; Prediction model; Grey relational grade; BP neural network; Markov method.

我國的工業生產水平逐步提高，同時又大力提倡節能環保及低碳排放，天然氣作為一種清潔、熱值高的能源，其年消費量呈逐年遞增的趨勢[1]。相對于我國天然氣消費量的增長速度，我國天然氣產量的增長速度較為緩慢，為了避免出現天然氣不能滿足于工業及民用的情況，很有必要對天然氣消費量進行有效預測，預測的效果好壞在很大程度上會影響到我國的工業發展以及居民生活，因此很有必要建立一個高精度的預測模型[2]。

近些年來，國內外學者們對天然氣消費量的預測方法進行了深入學習與研究，隨著研究的深入，研究人員所采用的方法得出的預測數據精準度越來越高。總體上，通過兩類方式對天然氣年消費量進行預測，一是物理方法，物理方法多利用天氣預報的結果如溫度、濕度、風速、云量等物理信息建立刻畫天然氣消費量的模型進行預測;二是統計方法，即采用計算機技術結合數學知識來建立新的模型進行對天然氣消費量的有效預測，常用的統計方法有：BP神經網絡模型、支持向量機模型、灰色理論模型以及時間序列模型等[3]。物理方法只需要較少的實際數據，但由于外界因素對其預測的數值影響較大，因此預測精度不是很高，而統計方法則是通過對歷史數據的分析，獲知隱含在數據中的規律，進而建立主觀模型，然后通過主觀模型進行有效預測[4]。

董明亮等通過對天然氣消費量的影響因素進行分析，采用遺傳算法和交叉驗證方法分別對支持向量機模型的懲罰因子c及核函數參數g進行優化，將優化后的參數輸入支持向量機模型中，提高了天然氣長期負荷預測的精準度[5]。宋娟等提出利用K-近鄰算法對燃氣負荷樣本中離群數據進行查找定位，并用特征曲線法對離群數據進行修正，再建立基于SVM（Support Vector Machines）的天然氣日負荷預測模型，并采用果蠅優化算法優化SVM的模型參 數[6]。宋超等分別利用Elman神經網絡和BP神經網絡預測模型對某企業的天然氣負荷數據進行仿真[7]。

前人對天然氣消費量進行預測時，在研究中考慮到影響因素相對比較少，而且很少對影響因素與天然氣年消費量的關聯度進行分析;有些研究方案在對天然氣年消費量進行預測的同時，沒能對預測結果進行有效地修正。因而，在本文中提出一種基于灰色-BP神經網絡以及馬爾科夫算法的預測方法。

1? 灰色關聯

1.1? 灰色關聯理論

灰色關聯度是兩個（或幾個）因素間關聯性大小的量度，關聯度表明了影響某事物發展的各因素間相互制約影響的程度，例如不同影響因素相對于天然氣消費量的變化幅度與變化速率等[8]。灰色關聯度實際上是比較數據曲線的幾何形狀的接近程度，幾何形狀越接近，變化趨勢就越接近，關聯度就越大。灰色關聯分析是通過計算出各因素間的灰色關聯度，對其影響程度進行了解，再選擇某些影響因素后進行深入研究，進而獲取其發展規律的一種方法[9]。

1.2? 灰色關聯度計算

下面對灰色關聯分析的計算步驟做進一步介紹。

1.3? 灰色關聯度分析

因為天然氣與煤炭、原油等能源構成了一個影響我國工業及居民生活的能源結構，其他種類能源的消費情況發生變化，往往會引起我國天然氣消費量的變化。因此，本文中將我國歷年的煤炭、原油、汽油、柴油、燃料油、電力消費量作為對天然氣消費量預測研究的影響因素，表1是我國2000-2015年天然氣年消費量及主要影響因素。

根據表1中的數據可以地表述出各能源消費量之間的關聯情況，由于各類能源消費量數據的計量單位的不一致性，導致在數值上具有較大的差距，為了滿足在同一幅圖上完整、清晰地展現出各類能源消費量的具體情況，以實現對各影響因素的關聯度進行初步篩選，因此將各類能源消費量在數值上進行相應處理，具體操作為：煤炭消費量、原油消費量以及柴油消費量的數值保持不變，汽油消費量和電力消費量的數值統一放大10倍，燃料油消費量數值統一放大100倍，天然氣消費量數值統一放大100倍，經調整后的各能源消費量具體情況如圖1所示。

由圖1可以看出天然氣年消費量在2000年至2015年間呈逐年遞增的趨勢，在前五年內增速較為緩慢，但由于我國工業以及城鎮的快速發展，以及響應國家號召加大對清潔能源的使用，在后10年內增速明顯提高;電力消費量以及煤炭消費量在15年里呈增長趨勢較為明顯，在近五年間，增長幅度更是與天然氣年消費量的增長趨勢很相似;汽油消費量、原油消費量以及柴油消費量雖然逐年遞增，但增速相對平緩一些;然而燃料油消費量的波動性較大，多次出現上升下降的波動趨勢。為了進一步準確地描述各能源消費量間的關系，通過灰色關聯計算各影響因素與天然氣年消費量的灰色關聯度。

通過對影響我國天然氣消費量的幾個因素進行灰色關聯度分析后，可得到各個因素與我國天然氣年消費量的關聯度，具體關聯度如表2。

由表2可知和天然氣年消費量關聯度較大的影響因素為原油消費量、汽油消費量以及柴油消費量，因此選取原油消費量、汽油消費量以及柴油消費量作為BP預測模型的輸入變量。

2? BP神經網絡

2.1? BP神經網絡理論

首先，以日、周、月等單位進行計量的天然氣消費量均具有一定的周期性;其次，節假日、氣候溫度以及天氣都對天然氣年消費量具有一定影響，這些因素會導致天然氣消費量的數據趨于不穩定，具有一定隨機性，因此利用傳統的線性預測方法，通過簡單的方程式計算還不能全面獲知其變化規律，預測誤差往往較大[10]。BP神經網絡是一種多層前饋網絡，它具有非線性逼近、自適應學習能力，它由一個輸入層、一個或多個隱含層和一個輸出層構成，每層由一定數量的神經元構成[11]。BP神經網絡不但可以對天然氣消費量的周期性進行準確描述，還可以反映出各因素對天然氣消費量的影響作用，適用于對我國天然氣消費量的預測。BP神經網絡的結構圖如圖2所示，BP神經網絡訓練流程圖如圖3所示。

2.2? BP神經網絡模型建立及結果分析

研究中所使用的數據為我國2000年至2015年的能源年消費量，預測模型的輸入訓練樣本為2000年至2007年的能源年消費量，輸出測試樣本為2005年至2013年的天然氣年消費量，其中包括訓練用過的2005年至2007年的天然氣年消費量。

本文所要建立的天然氣年消費量預測模型是輸出單元為1的特殊模型，利用premnmx函數對輸入變量和目標函數集進行歸一化處理，通過newff函數建立一個前饋BP神經網絡，采用train函數進行網絡訓練，由于輸出變量與輸入變量的關系比較復雜，因此可對隱含層的神經元數進行適度增加，通過多次訓練及調整，最終確定隱含層為8個隱層節點。

首先將未經灰色關聯度分析篩選的數據樣本作為輸入樣本進行預測，其中考慮的樣本包括2000年至2007年的天然氣、煤炭、原油、汽油量、柴油、燃料油、電力消費量;再將經過灰色關聯度分析篩選的數據樣本作為輸入樣本進行預測，其中考慮的樣本包括天然氣消費量、原油消費量、汽油消費量以及柴油消費量。預測結果如圖4所示。

其中預測值一是通過對影響因素進行分析篩選所得出的預測值，預測值二是未對影響因素進行分析篩選所得出的預測值。

由圖4可以看出，對各因素進行篩選后作為輸入變量的預測精度更高，預測數值擬合的曲線更加接近于真實值，而未對因素進行篩選的預測結果誤差較大，擬合形成的曲線與實際數據擬合的曲線具有較大偏差。采用兩種方式預測出的天然氣年消費量的具體數值以及預測的相對誤差如表3、表4所示。

3? 馬爾科夫過程

3.1? 馬爾科夫理論

利用BP模型進行長期預測時，如果用于訓練的歷史數據往往具有較大波動性，得出的預測結果誤差較大[12]。而馬爾科夫則是針對數據具有一定隨機性的系統進行預測的，馬爾科夫法首先對事物發展狀態的轉移概率進行考慮，轉移概率反映出各種隨機因素間的影響程度，再通過事物狀態之間的轉移概率來對事物未來的發展進行判斷，其思路是對光滑的預測曲線進行劃分，分為不同的狀態區間;根據落入各狀態區間的時間點計算出馬爾科夫轉移概率矩陣;取預測值所處狀態區間的中間點對預測值進行修正，進而提高預測值的預測精度[13]。

通過馬爾科夫法對天然氣年消費量預測結果進行修正的步驟：

1）預測模型對天然氣年消費量進行預測，計算并分析天然氣年消費量的預測誤差，將其按照N個狀態進行劃分;

2）上一步對狀態的劃分，統計天然氣年消費量預測誤差的狀態轉換情況，得出適用于此次預測的狀態轉換頻數矩陣;

3）上一步得出的狀態轉換頻數矩陣進而推算出狀態轉換概率矩陣;

4）采用預測模型對未參與上一次預測的天然氣年消費量數據進行預測，通過狀態轉換概率矩陣對天然氣年消費量進一步的預測值進行修正;

5）修正后的預測值與實際值進行對比，再次計算預測誤差。

3.2? 馬爾科夫矩陣計算

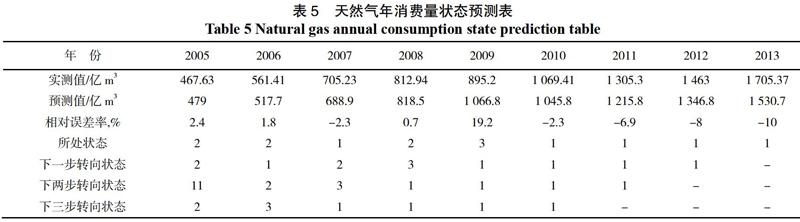
由馬爾科夫理論可以得知，對事物發展的狀態劃分會影響到預測結果，即狀態劃分的不同會引起預測結果的側重點不同[14]。由復雜系統理論可以得知，研究中通過定量與定性相結合的方法對事物發展趨勢進行預測，是為了讓兩種方式得到的預測結果進行相互補充以及檢驗。在對于我國天然氣年消費量所進行的預測，定性預測的思想是： 將天然氣消費量的預測誤差的發展狀態分為上升和下降兩種，預測結果表明的是天然氣消費量預測值的誤差相對于前一時間段的發展狀態是上升或下降;定量預測的思想是： 將天然氣年消費量發展狀態分為3種，狀態1為[-15%，0），狀態2為[0，15%），狀態3為[15%，30%]，狀態1表示對于預測誤差的低估，狀態2表示對于預測誤差的高估，狀態3表示對于預測誤差的過度高估[15]。通過馬爾科夫進行預測的建模思想為：首先對天然氣年消費量的預測誤差發展狀態進行定性分析，即為升或降;再對天然氣年消費量的預測誤差發展狀態進行性分析，預測結果表明在下一時間段，天然氣年消費量的預測誤差將處于某一狀態，再根據所處的狀態對天然氣消費量的預測值進行誤差修正。根據采用BP 神經網絡模型進行預測得出的結果可以得到天然氣消費量狀態預測表，如表5所示。

根據天然氣年消費量狀態預測表可以得出狀態轉移概率矩陣，根據不同步數的轉向可得到相應的狀態轉移概率矩陣，狀態轉移概率矩陣如下所示，R1、R2、R3分別為經過1步、2步、3步所得到的狀態轉移概率矩陣。

3.3? 馬爾科夫矩陣的修正

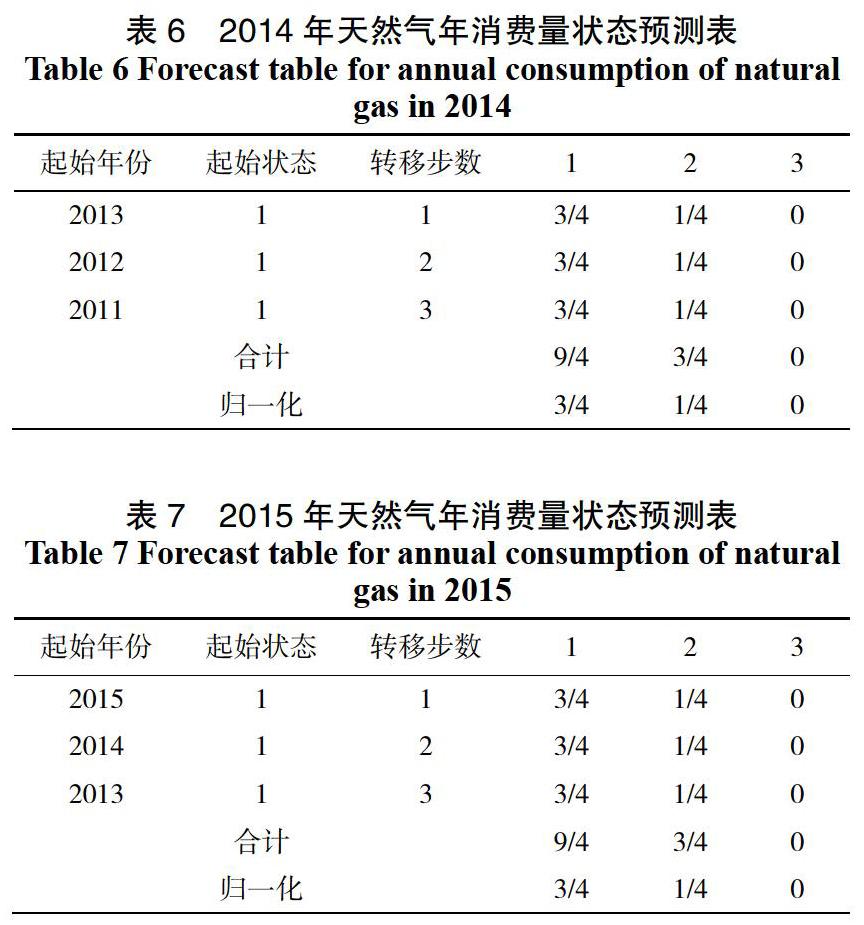
取離預測年份2014及2015年最為接近的 3個年份，根據距離預測年份的遠近，轉移的步數分別為：1、2、3，并在各個轉移步數所對應的轉移矩陣中，取其起始狀態所對應的行向量，組成新的概率矩陣，并對該概率矩陣的列向量求和，確定系統未來轉向狀態[16]。由天然氣年消費量狀態預測表以及狀態轉移概率矩陣可以得到2014年以及2015年的天然氣消費量狀態預測表，表6為2014年的天然氣消費量狀態預測表，表7為2015年的天然氣消費量狀態預測表。

根據以表6可知在合計一欄中以狀態 1的概率最大，因此可以預測2014年的天然氣年消費量的預測誤差處于狀態1，進而對預測值進行修正，可推算出2014年的天然氣年消費量為：

1 576.1×（1+1/2×15%）=1 694.31（億m3）。

同理，根據以表7可知在合計一欄中以狀態 1的概率最大，因此可以預測2015年的天然氣年消費量的預測誤差處于狀態1，進而對預測值進行修正，可推算出2015年的天然氣年消費量為：

1 634×（1+1/2×15%）=1 756.55（億m3）。

進而可以得出表8、表9基于2種模型的天然氣年消費量預測表，其中模型1為BP神經網絡模型，模型2為經馬爾科夫矩陣修正的BP神經網絡模型。

由表8和表9可知經馬爾科夫矩陣修正的BP神經網絡模型預測精度要優于BP神經網絡模型，相對誤差有所減小。

4? 結 論

本文首先應用灰色關聯算法對天然氣年消費量的影響因素與天然氣年消費量的關聯度進行計算，選出影響作用大的因素作為BP預測模型的輸入變量，通過BP預測模型預測天然氣的年消費量，對比預測值與實際值之間誤差推算出馬爾科夫矩陣，再利用馬爾科夫矩陣對BP預測模型的進一步預測進行修正，由本文的計算得到以下結論：

1）采用多影響因素進行預測的效果往往好于單一影響因素預測的效果，但關聯度小的影響因素往往會降低預測精度，對多種影響因素進行篩選后作為輸入變量，預測精度有明顯提高。

2）BP神經網絡對于變化比較活躍、具有一定波動性的數據進行預測時，預測精度不夠，但通過馬爾科夫法對預測數據的的誤差進行分析后，可對數據間的變化規律進一步了解，再對BP模型得出的預測數據進行進一步修正，修正后預測精度有提高趨勢。

3）為以后對天然氣年消費量的預測提供了一種新的方法，對于預測天然氣消費量的季度、月以及周的負荷預測也具有一定的參考價值。

參考文獻：

[1]胡彪，張旭，梁金川.我國天然氣產業鏈發展現狀研究[J].當代化工，2016， 45（5）：971-973.

[2]張濤，楊嬌敏.我國區域天然氣消費量的趨勢預測[J].天然氣工業，2016， 36（9）：135-140.

[3]喬偉彪，陳保東，吳世娟. 基于小波變換和LSSVM-DE的天然氣日負荷組合預測模型[J].天然氣工業，2014，34（9）：118-124.

[4] 何春蕾，段言志，鄔宗婧，等.基于氣溫的城市燃氣短期日負荷預測模型-以四川省成都地區為例[J].天然氣工業，2013，33（4）：131-134.

[5]董明亮，劉培勝，潘振，等.基于SVM-GA模型的城市天然氣長期負荷預測[J].遼寧石油化工大學學報，2017，37（2）：31-36.

[6]宋娟，潘歡.基于果蠅算法和SVM 的天然氣日負荷預測[J].控制工程，2017，24（10）：1995-2002.

[7]宋超，宋娟，任軍.基于Elman神經網絡的短期天然氣負荷預測建模與仿真[J].工業控制計算機，2016，29（4）：87-88.

[8]趙曉琴，康正坤，吳鳳榮.天然氣消費的影響因素及灰色關聯分析[J].油氣儲運，2008，27（8）：5-8.

[9]孫鵬霄.灰色關聯方法的分析與應用，數學的實踐與認識[J].2014，44（1）：97-101.

[10]宋超，宋娟.算法優化和BP神經網絡的短期天然氣負荷預測[J].工業控制計算機，2012，25（10）：82-84.

[11]周彩蘭，劉敏.BP神經網絡在石油產量預測中的應用[J].武漢理工大學學報，2009，31（3）：125-129.

[12]陳廣銀，蔡灝兢，姜欣.馬爾可夫修正的 BP 神經網絡在PM2.5預測中的應用[J].能源環境保護，2017.31（5）：8-11.

[13]陳釗，徐阿猛.基于灰色馬爾科夫模型的鉆孔瓦斯流量預測[J].中國安全科學報，2012，22（3）：79-85.

[14]陸興華，姜濤，秦斯成.改進灰色馬爾科夫模型在煤層沉降預測中的應用[J].煤炭技術，2015，34（1）：188-191.

[15]趙振武，麻建軍.基于灰色馬爾科夫模型的機場安檢危險品數量預測[J].安全與環境學報，2017，17（1）：51-53.

[16]李靖，張瑞新，李澤荃.改進的灰色模型在露天煤礦安全隱患預測中的應用[J].華北科技學院學報，2019，16（3）：67-72.