環型圓管內對流動力學行為及數值分析

王賀元, 楊躍男, 柏孟卓

(沈陽師范大學 數學與系統科學學院, 沈陽 110034)

混沌是非線性系統特有的一種運動形式,產生于確定性系統的依賴于初始條件的往復穩態非周期運動,類似于隨機振動而具有長期不可預測性[1]。1963年,氣象學家洛倫茲在數值實驗中發現混沌現象,隨后,經過Kuhu、Li、和Yorke以及May等對混沌的進一步研究,到近代的呂金虎、陳關榮等又提出統一混沌系統[2]。這些開創性工作對混沌理論的應用起到了至關重要的推動作用。混沌理論在眾多領域均有廣泛的應用,如環型圓管內的對流問題:豎直放置的環型圓管內充滿流體,環境溫度下熱上冷,當底部溫度達到一定值時,管內流體發生對流現象。本文通過分析和仿真環型圓管裝置所對應的數學模型的動力學行為,分析解釋了圓管內的對流現象。

1 環型圓管對流的數學模型

豎直放置的環型圓管內充滿流體,環境溫度下熱上冷。開始流體靜止,上下流體內的溫差到達一定值后,流體開始在管內對流耗散,忽略粘性流體運動時能耗所產生的熱量,并假定通過管壁的熱傳導速率正比于流體溫度與壁外環境溫度的差,得出能量方程的近似分解式[3]。文獻[3]給出了該數學模型的動力學方程式:

(1)

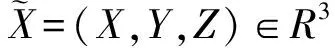
1.1 系統的對稱性和不變性

該類洛倫茲系統具有對稱性,即在變換(X,Y,Z)→(-X,-Y,Z)下具有不變性,系統(1)關于Z軸具有對稱性,且這種對稱性對所有的系統參數均成立[4]。

1.2 耗散性和吸引子的存在性

1.3 平衡點及穩定性

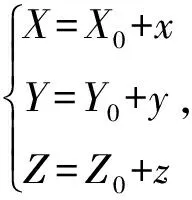
再線性化,就得到該平衡點的穩定性方程為

將(X0,Y0,Z0)=(0,0,0)帶入穩定性方程,得該點的雅可比矩陣為

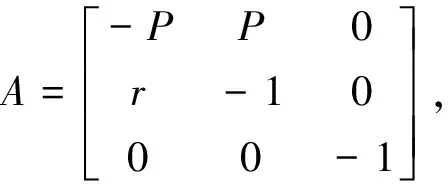
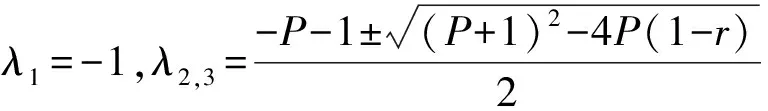
當01時,λ的2個根為負實數,一根為正實數,因此(O)是不穩定的,因此r=1是一個過渡點。(O)在該點從穩定過渡到不穩定。同時,在這一過渡點上,新的平衡點(C1)和(C2)開始出現。

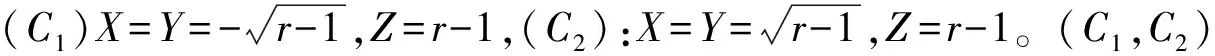
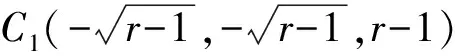
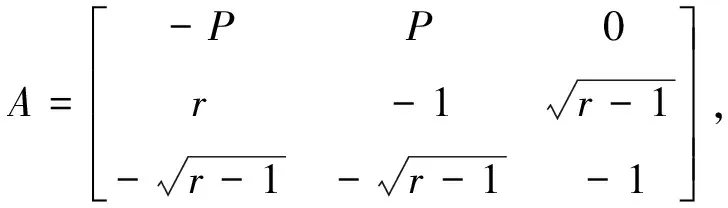
特征方程為λ3+(2+P)λ2+(r+P)λ+2P(r-1)=0。

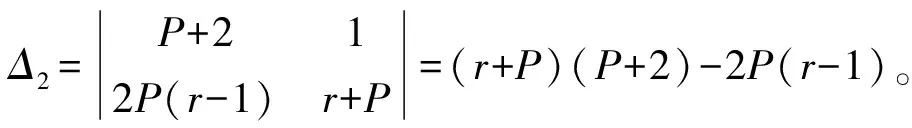
2 系統參數的影響

根據上面的分析,隨著系統參數的改變,系統平衡點的穩定性也發生變化,從而系統將處于不同的狀態[9]。下面進行分岔及軌道的討論與分析。

當r≤r1=1時,只有一個定點O(0,0,0),它是穩定的。當r>r1時,O變為不穩定,同時出現了另外2個穩定的定點C1和C2,故在r=r1=1時出現音叉分岔。當rrh時共軛復根的實部變為正的。可見r=rh是霍普夫分岔點,這時環型圓管發生渦流現象,是正臨界霍普夫分岔,分岔形成的極限環是不穩定的[10]。即當r>rh時,圍繞C1和C2可能出現不穩定周期解,這種不穩定極限環在系統內的起伏作用下,將轉變為其他形式的運動,也就是混沌[11],即此時環型圓管內的流體的運動方式為混沌運動,這對應于環型圓管內當底部溫度逐漸升高時,流體由靜止到失穩,從對流到湍流的復雜流動。

3 系統的分岔與混沌的數值模擬

隨著雷諾數r的增大,類洛倫茲系統(1)的動力學行為發生了一系列變化,如出現霍普夫分岔和混沌等非線性現象[12]。首先,對系統(1)進行數值求解,進而畫出仿真圖以揭示系統的混沌行為。圖1給出了狀態變量x隨r變化的全程分岔圖,展示了系統分岔和混沌演變的全過程,系統通過陣發途徑發生混沌,在混沌中出現了3個周期窗口,說明此系統的周期運動比較穩定[13]。圖2給出了系統隨參數r變化的最大Lyapunov指數譜。從圖中可以看出最大Lyapunov指數大于零的區域與分岔圖1顯示的混沌區域是一致的[14]。

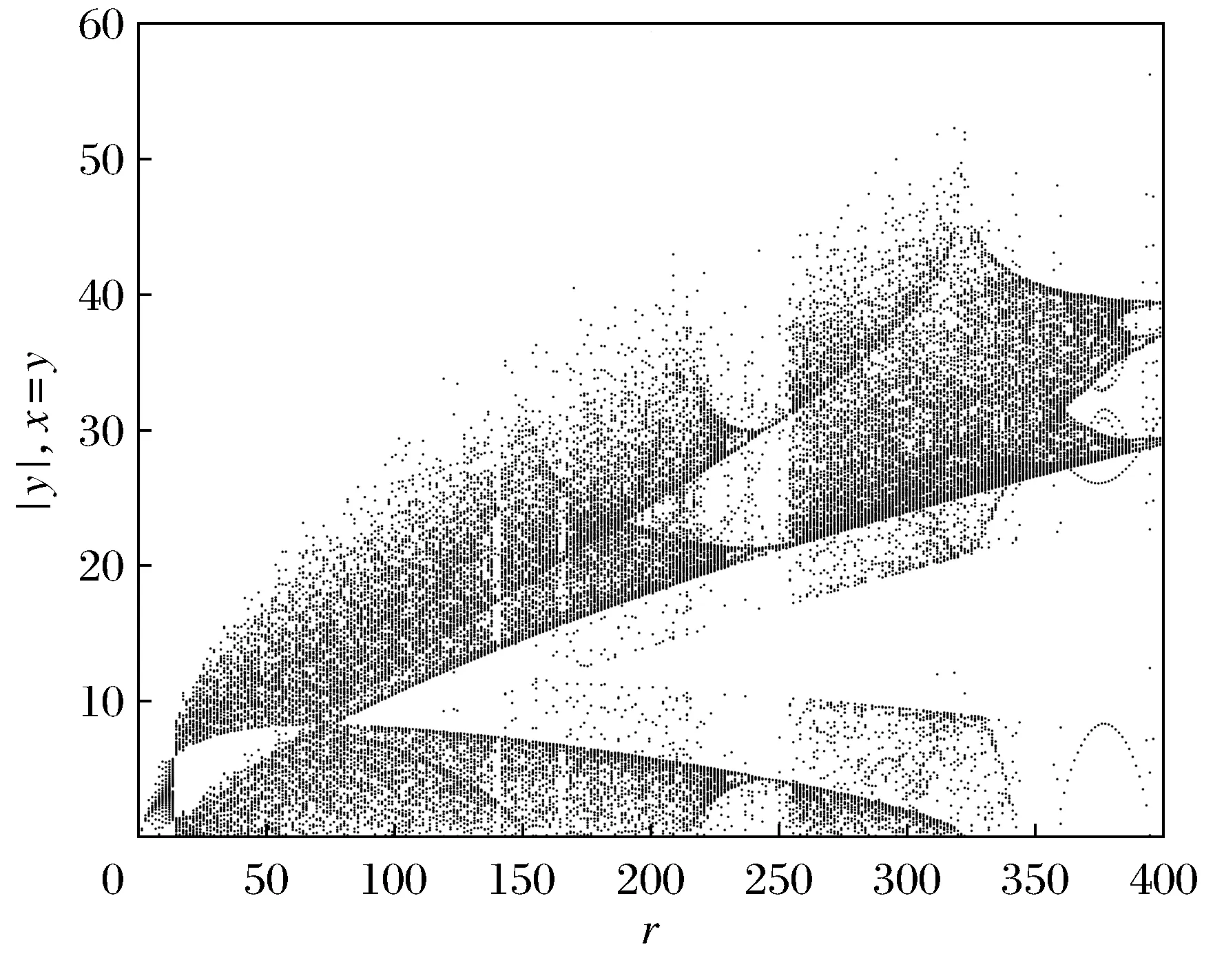
圖1 系統(1)雷諾數在0≤r≤400范圍內狀態變量x的分岔圖

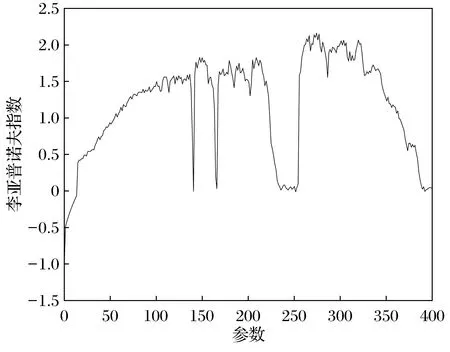
圖2 系統(1)雷諾數在0≤r≤400范圍內最大Lyapunov指數圖

4 結 論

本文研究了環型圓管內的流體對流的三模態類洛倫茲型方程組的部分動力學行為。數值模擬了由不穩定周期到達混沌所展現的動力學行為。仿真結果表明,此系統隨著參數增加,由不穩定的周期軌道經暫態混沌直接進入混沌狀態。相對應的物理現象表現為隨著底部溫度的逐漸升高,管內流體發生復雜的對流現象。環型圓管的對流行為是由于雷諾數r的不斷增大產生,在此過程中系統發生由穩定的不動點到周期軌道,再失去穩定性進入混沌區域[15]。

致謝感謝沈陽師范大學博士啟動基金項目的支持(054-91900302009)。