基于二氧化碳工質的回熱器振蕩流實驗與模擬研究

陳 欣，肖 剛，童良懷，孫安葦，倪明江

（1.浙江大學能源工程學院，浙江 杭州 310027；2.衢州市特種設備檢驗中心，浙江 衢州 324002）

斯特林發動機（Stirling engine）因具有廣泛的能源適用性且污染物排放易于控制，在余熱利用、太陽能光熱發電、水下動力等領域具有巨大的應用潛力[1]。作為一種閉式循環外燃機，長時間安全穩定地運行是評價斯特林發動機的重要指標。

氫氣、氦氣和二氧化碳均可作為斯特林發動機的循環工質。從安全性角度來說，氫氣化學性質過于活潑，而斯特林發動機內部壓力較大，采用氫氣為循環工質時較為危險，不利于小型斯特林碟式系統的推廣。從經濟性角度來說，氫氣和氦氣獲得成本較高，市面上的氫氣和氦氣價格分別是氮氣和空氣價格的4倍和35倍。從密封性角度來說，利用已有的100 W斯特林發動機進行各工質的密封測試，發現二氧化碳介質在斯特林發動機中的密封性能最好[2]。從效率角度來說，在轉速較低時，使用二氧化碳作為工質的循環效率更高[3]。因此，在斯特林發動機中采用二氧化碳作為工質，適用于分布式熱電聯用系統，開發潛力巨大。

回熱器是斯特林發動機的核心部件之一，其效率將對整機效率產生很大影響。倪明江等[4]采用改進型的Simple模型分析了100 Wβ型斯特林發動機，發現在研究工況下，回熱器流阻損失占功率損失（功損）的20%，回熱器導熱損失占總能量損失的65%以上；Babaelahi和Sayyaadi[5]分析了GPU-3斯特林發動機內部的流阻損失，發現回熱器的峰值壓降是加熱器和冷卻器峰值壓降和的8倍（頻率41.67 Hz、壓力4.14 MPa），并且換熱器壓降引起的功損占總功損的76.8%。已有一些學者針對常用的斯特林循環分析方法中計算流阻損失的關聯式進行了研究，如表1所示。

表1 常用的斯特林循環分析方法中計算流阻損失的關聯式Tab.1 The correlations for flow resistance loss calculation in common Stirling cycle analysis methods

表1中關聯式主要是針對空氣、氦氣的流動特性，并未對二氧化碳進行相關研究。目前，二氧化碳工質在回熱器中的流動特性尚不明確，無法利用相關分析方法設計和優化基于二氧化碳工質的斯特林發動機。

Peng等人[13-14]發現，在1個循環中，不同截面的質量流量不同。因此他們對各截面1個循環內的質量流量進行積分，得到工質的循環質量Mcr；再通過各截面的Mcr與理論循環質量Mct之比，提出循環率δ的概念。由此可以快速準確地計算出進入回熱器的真實質量流量，以此設計效率更高、流阻更小的回熱器。

為了開發二氧化碳工質斯特林發動機，提高回熱器性能、機器效率和功率，完善斯特林循環分析方法，本文將針對二氧化碳氣體在金屬絲網回熱器內部的流動特性開展系統研究，以獲得氣體循環率修正的定量方法，指導基于二氧化碳斯特林發動機的優化設計。

1 研究方法

1.1 研究思路

目前，對于回熱器內氣體工質振蕩流的研究方法主要分為2種：一種是忽略金屬絲網的實際結構，借助多孔介質模型簡化計算過程，該方法依賴2個阻力系數，精度較差，且無法獲得真實流場細節；另一種是在計算域中直接考慮金屬絲網的實際結構，采用基于精細網格的有限體積方法（FVM）直接計算獲得接近真實結構的流場細節。

本文采用有限體積方法，建立考慮實際金屬絲網細節結構的CFD模型，計算二氧化碳與金屬絲網的摩擦系數。然后，搭建回熱器振蕩流實驗臺，并建立完全相同的回熱器振蕩流模型（采用Fluent多孔介質模型），比較壓降、壓力結果，驗證模擬的準確性。最后，對二氧化碳循環率進行研究。研究思路如圖1所示。

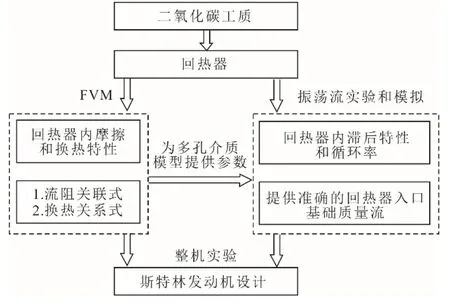
圖1 本文研究思路Fig.1 The research idea of this paper

1.2 幾何模型和邊界條件

建立模型，采用一類結構2層、二類結構3層的方式，交錯堆疊，每層是橫縱3條纏繞金屬絲。20、100、200、400目絲網絲徑分別為1、0.1、0.03、0.015 mm，孔隙率分別為0.85、0.65、0.63、0.53。流域總長是4倍絲網長度，兩側各1.5倍。Costa[10]、賴華盛[15]等人已經驗證了5層絲網的準確性。圖2是200目絲網的最終模型。為了更為準確地監測氣體經過絲網后的溫度、速度、壓力等變化并反映氣體與絲網的流動和換熱過程的瞬時變化，在離絲網實體0.5倍絲徑距離處建立了監測面1和監測面2（見圖2d)）。

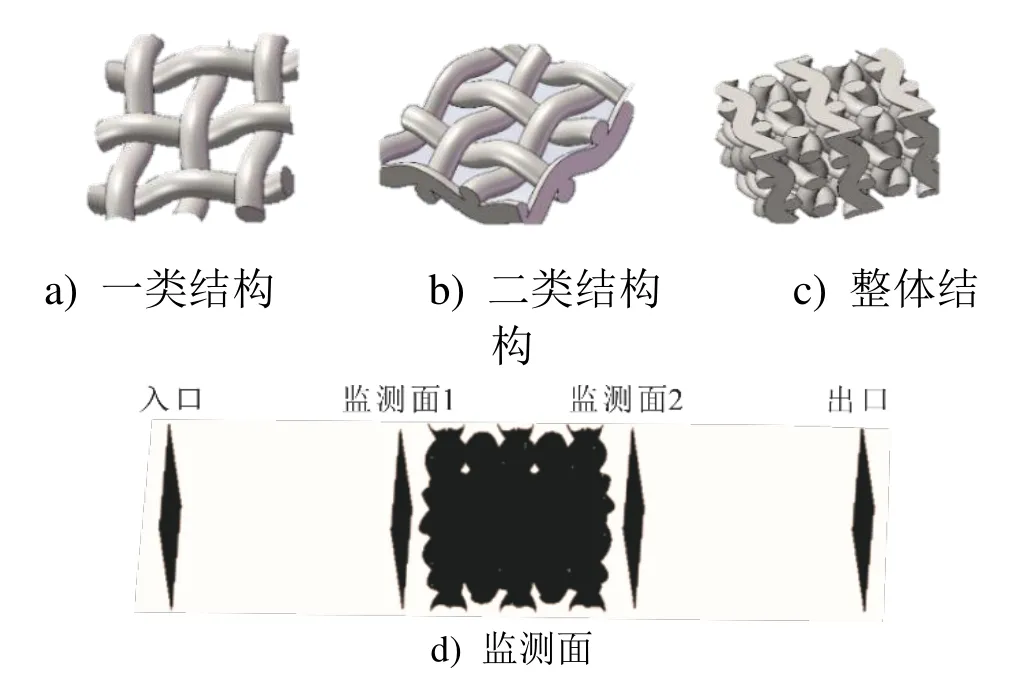
圖2 金屬絲網結構Fig.2 The structure of the wire mesh

內部氣體的密度、黏度、熱導率和比熱容通過REFPROP軟件進行擬合。入口采用速度入口，出口采用壓力出口，金屬絲網實體壁面采用耦合壁面，流域壁面采用對稱壁面。時間步長通過頻率計算得到，經過時間步長、網格無關性驗證后取以曲軸轉過1°為1個時間步長。網格數目為200萬，網格質量大于0.5[15]。模擬工況見表2。

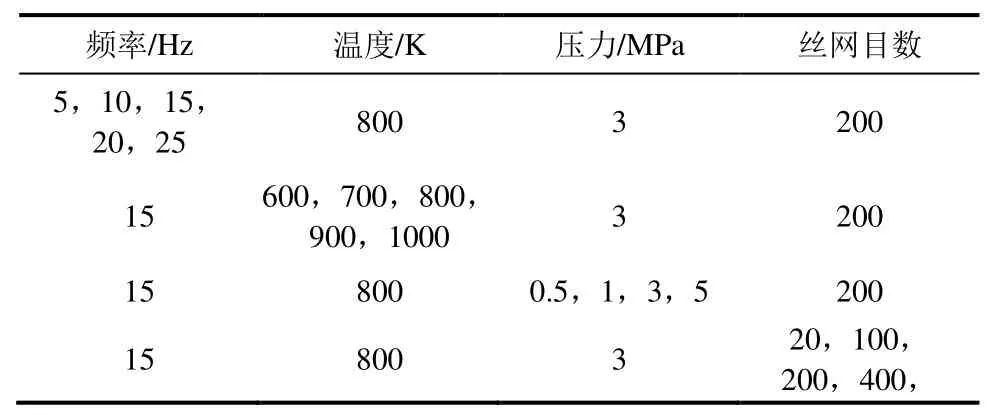
表2 二氧化碳工質模擬工況Tab.2 The simulation working conditions for CO2

1.3 數學模型

由于金屬絲網內部特征流通直徑較小，需要驗算是否滿足流體連續性假設。金屬絲網參數見表3。

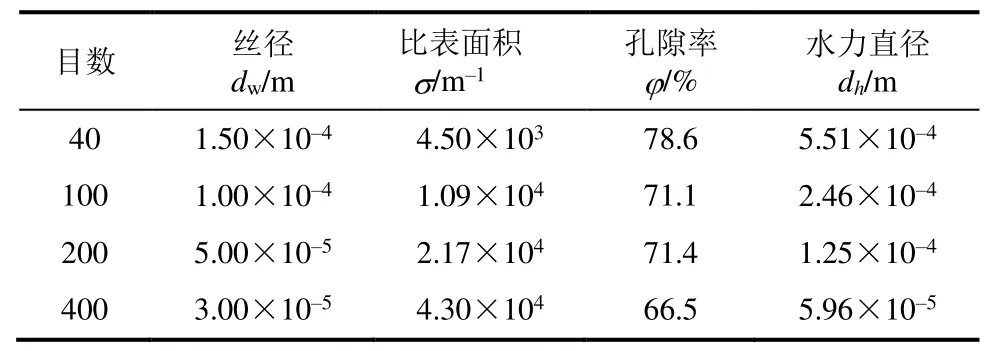
表3 金屬絲網參數Tab.3 The structural parameters of the wire mesh

氣體分子平均自由程計算公式如下[16-17]：

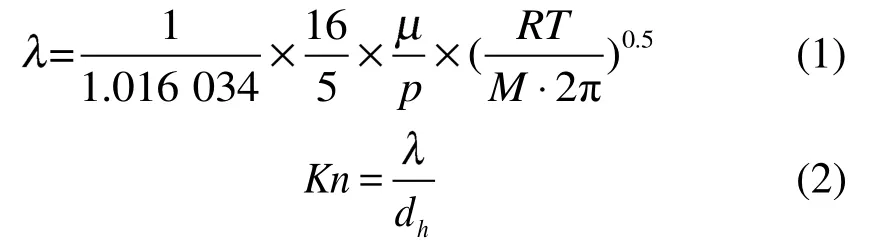
計算3個工況點（200目、0.5 MPa、800 K，200目、3 MPa、1 000 K和400目、3 MPa、800 K），分別得到。

由于克努森數Kn均小于0.01，因此在CFD模擬時可以采用連續性介質假設。

Fluent多孔介質模型中引入了2個參數（黏性阻力系數張量和慣性阻力系數張量）來描述動量方程（見式(3)），而回熱器是各向異性的，只考慮軸向流動，源項可以表示為式(4)。

式中：S為源項；Cf為黏性阻力系數張量，m2；Cj為慣性阻力系數張量，1/m；A、B、C為擬合系數；孔隙率；Redh為雷諾數；dh為特征長度，m；p為壓力，Pa；t為時間，s；為剪切應力，N。

目前，常用的流阻系數關聯式擬合式如式(8)、式(9)。2種形式的擬合公式均來自Ergun公式：當C很小時，在低雷諾數下A/Re占主導；但在高雷諾數下，B/ReC的存在使得f更為準確。因此，本文采用式(9)。

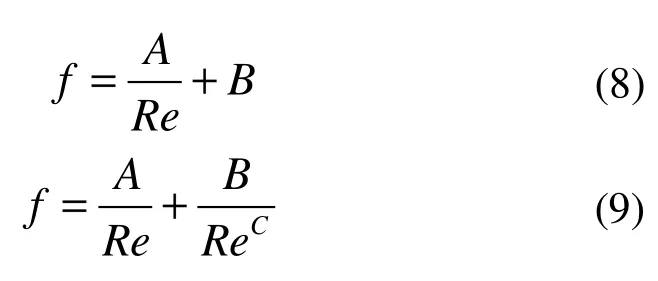
2 振蕩流實驗

2.1 實驗準備

為了驗證基于FVM的CFD方法得到的關聯式的準確性，并對二氧化碳循環率進行研究，搭建了圖3所示的振蕩流實驗臺，其主要結構和儀器參數以及實驗工況分別見表4和表5。

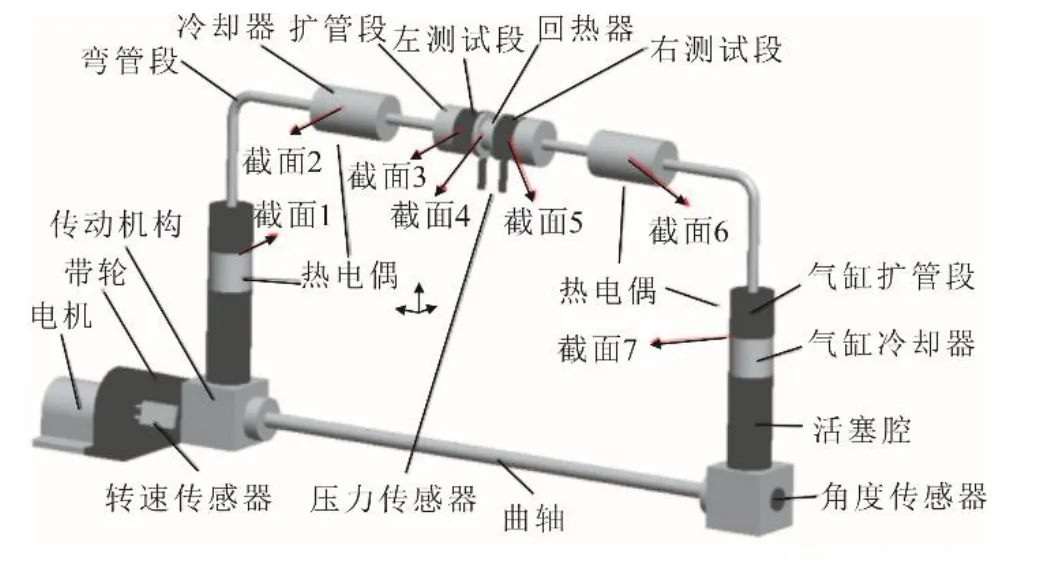
圖3 實驗臺示意Fig.3 Schematic diagram of the experimental bench

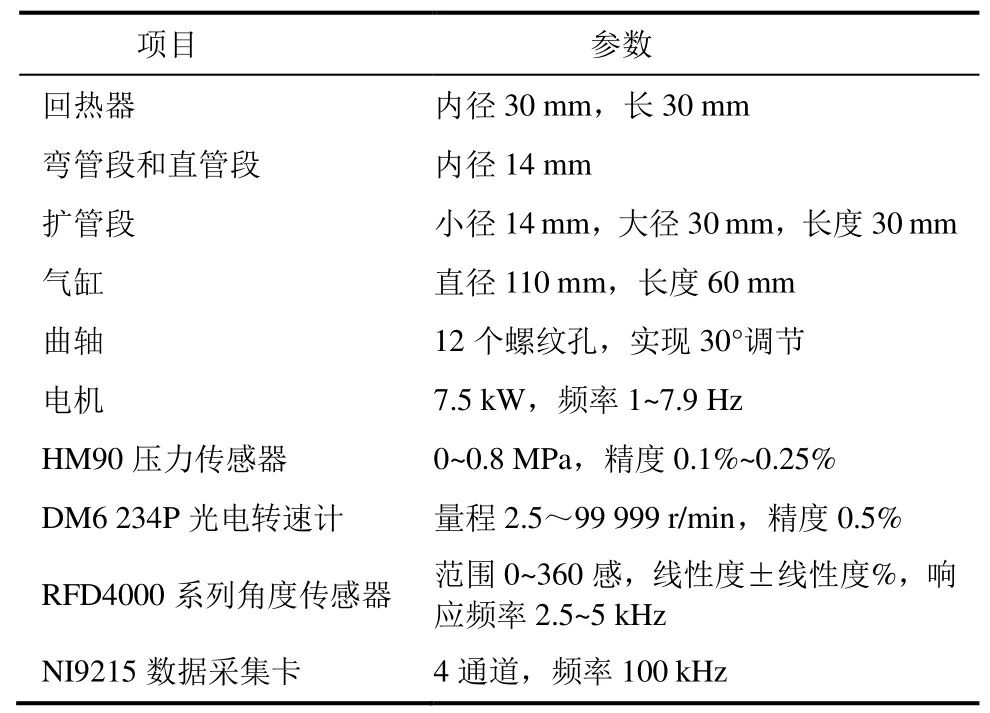
表4 實驗臺主要結構和儀器參數Tab.4 The main structural and instrumental parameters of the test bench

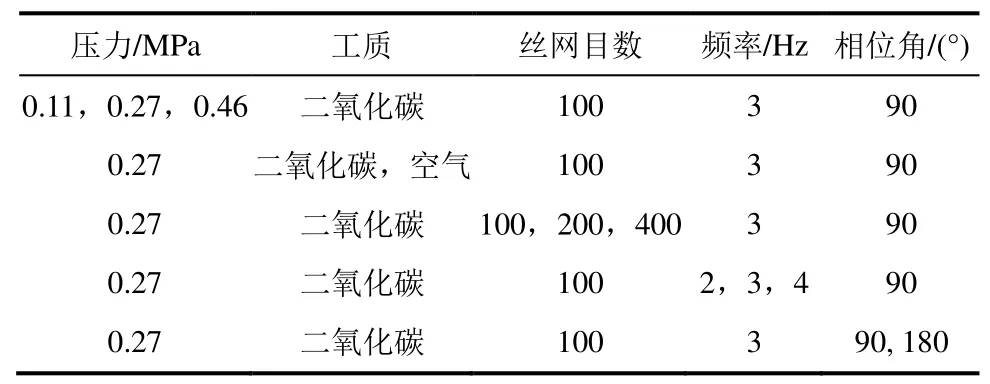
表5 實驗臺模擬和實驗工況Tab.5 The simulation and experimental working conditions for test bench

進行實驗前：先打開氣瓶的閥門和所有管路閥門，對整個裝置進行吹氣；30 s后，關閉裝置放氣閥門，使裝置充氣（空氣或二氧化碳）至0.6 MPa，靜置5 min；打開閥門降壓到0.2 MPa，啟動電機30 s，使內部氣體混合；再次充壓至0.6 MPa。如此反復3次，保證內部工質氣體的純度。此外，在前期的測漏實驗中發現，在裝置充壓至0.6 MPa時，40 min后壓力下降了0.02 MPa。為了解決密封性的影響，在氣瓶閥門后增加了一個單向閥，以保證內部最小壓力相同，減小實驗測量誤差。

開始實驗后：采集角度、壓力、溫度、速度等數據；之后啟動電機，電機帶動左側皮帶輪運動，然后通過曲軸使左活塞和右活塞進行垂直運動；而后調節電機轉速，通過轉速計確認轉速是否達到所需測量頻率；最后等待1 min，當氣瓶上減壓閥壓力示數不再波動后進行數據采集。

2.2 模擬獨立性驗證

為了驗證基于FVM的CFD模型以及3.4節實驗結果，按照實驗臺的實際尺寸，采用網格劃分軟件ICEM進行建模，之后再利用Fluent軟件進行模擬計算。

Study on Foreign Language General Education Curriculum Construction Strategy in Higher Vocational Colleges ___________________WANG Wenxuan,DING Guomao,FENG Yonghong 74

采用動網格模型，通過用戶自變量函數（UDF）導入，活塞速度為：

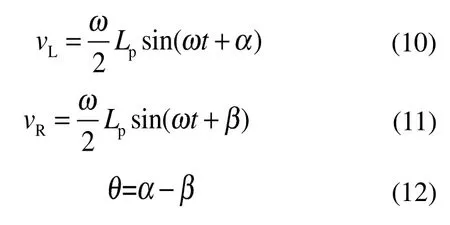
式中：vL、vR為左、右側活塞速度，m/s；角速度，rad/s；Lp為活塞行程，m/s；為相位角；為相位差。

采用k-湍流模型、二階迎風格式對壓力、能量等進行離散。內部氣體類型設置為理想氣體，其黏度、熱導率、比熱容等參數與孔隙尺度模擬一樣，通過REFPROP軟件進行擬合，擬合的壓力和溫度范圍由實驗確定。4個冷卻器壁面條件均為恒溫壁面，溫度由熱電偶測得，操作壓力為0，初始化內部壓力由壓力傳感器測得。

分別建立了100萬、300萬、500萬3種網格數量的模型對比回熱器兩端的壓降，如圖4所示。由圖4可知，300萬及以上數量網格模擬結果與實驗結果相差不大。因此，本文采用300萬網格。

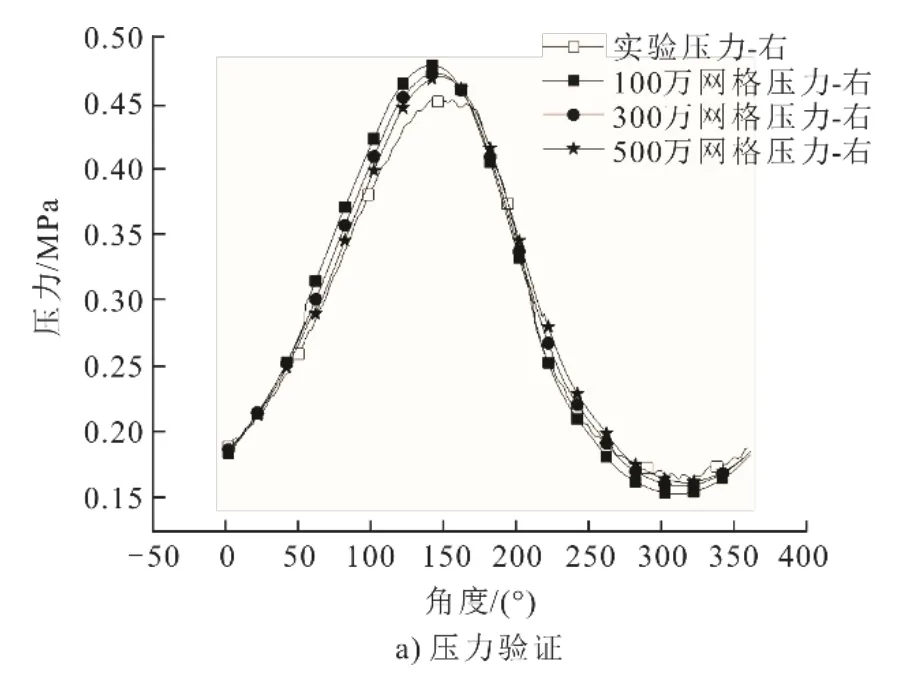
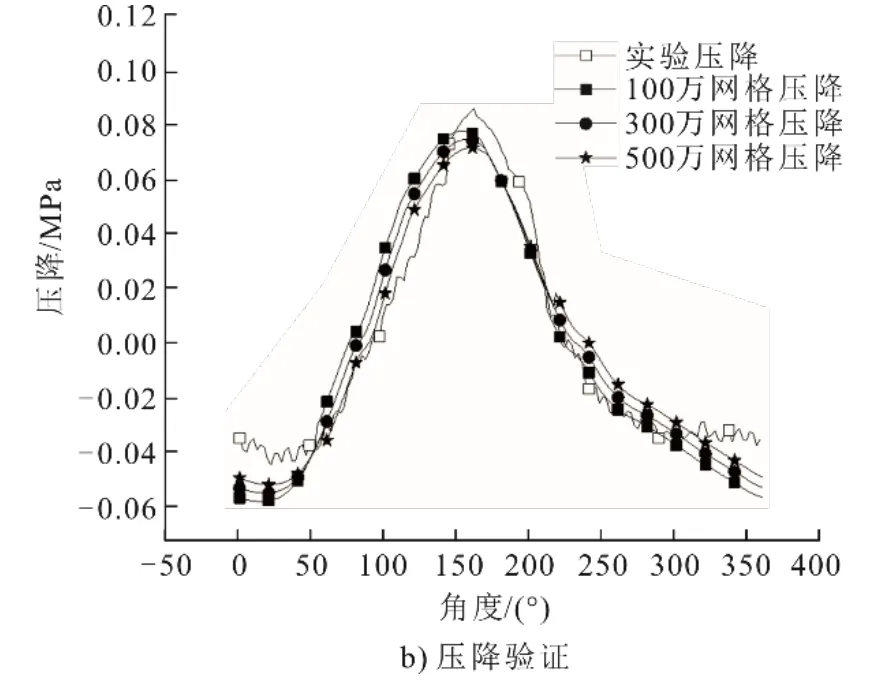
圖4 網格無關性驗證Fig.4 The grid independence verification

3 結果分析

3.1 基于FVM的CFD模型驗證

為了驗證基于FVM的CFD模型的準確性，對空氣進行了若干個工況（表6）的模擬，結果如圖5所示。

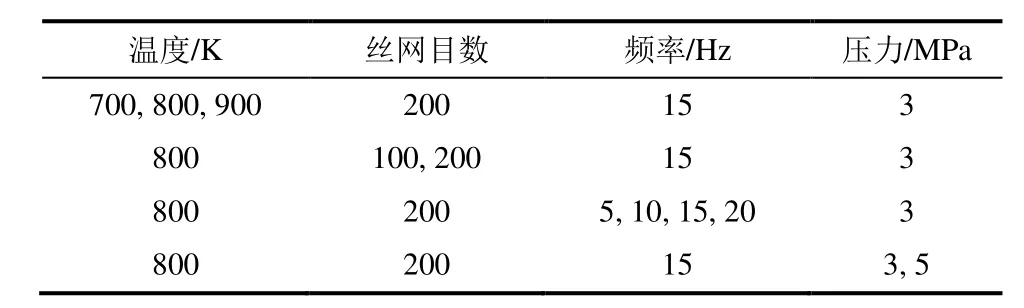
表6 空氣工質模擬工況Tab.6 The simulation working conditions with air

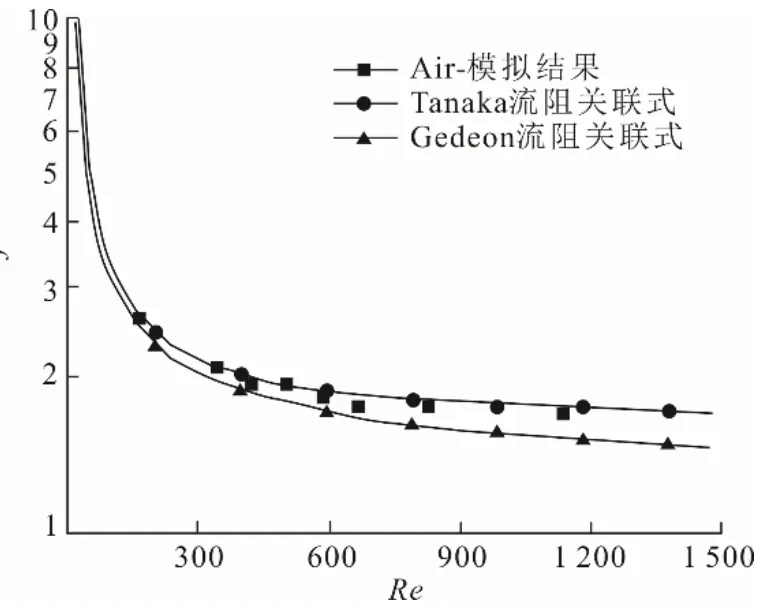
圖5 基于FVM的CFD模型空氣流阻系數驗證結果Fig.5 The verification result of air flow resistance coefficient by the FVM-based CFD model

表6中8個工況對應的雷諾數Re的范圍是162~1 156。由圖5可以看出：使用FVM模型得到的結果與Tanaka關聯式的誤差范圍為5.47%~0.36%；與Gedeon關聯式最大誤差為7.52%~4.06%。因此說明該FVM模型可以用于二氧化碳流動特性的研究。

3.2 壓降特性

3.2.1 溫度的影響

設定曲軸轉動前180°是熱吹過程，即熱氣體加熱冷絲網，后180°是冷吹過程，即熱絲網加熱冷氣體。不同熱端溫度下工質壓降變化如圖6所示。由圖6可以看出：壓降在熱吹過程中隨熱端溫度升高而下降，在冷吹過程中隨熱端溫度升高而升高。這主要是因為在熱吹過程中，熱端溫度高，進入回熱器的氣體密度相對較低，因此壓降較小；在冷吹時，進入回熱器氣體溫度均為300 K，密度相同，但熱端溫度越高的工況其回熱器絲網溫度也越高，內部湍流更為劇烈，所以壓降較大。

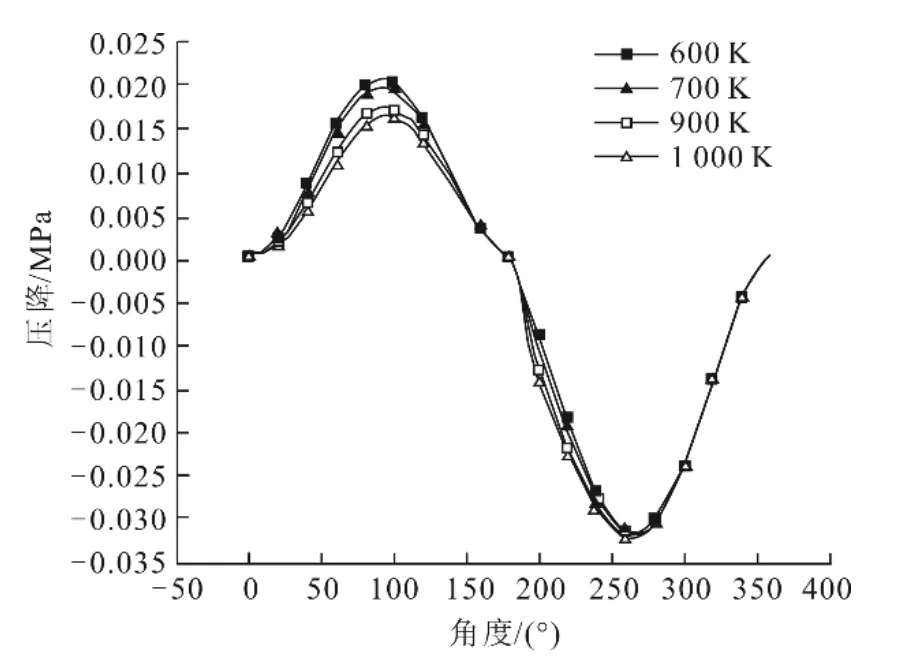
圖6 不同熱端溫度下工質壓降變化Fig.6 The pressure drop of working fluid at different hot-end temperatures

3.2.2 目數、頻率、初始充氣壓力的影響

不同目數、頻率、初始充氣壓力下工質的壓降變化如圖7所示。由圖7可以看出：目數越大，孔隙率越小，壓降越大；頻率越高，壓降越大；初始充氣壓力越大，壓降越大。

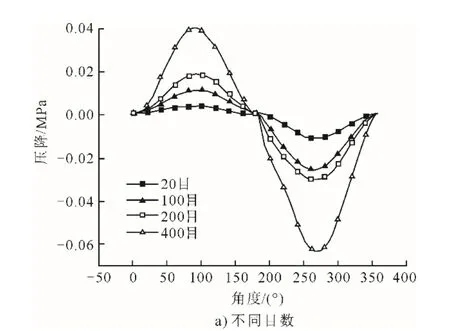
圖7 不同目數、頻率、初始充氣壓力下工質壓降變化Fig.7 The variations of working fluid’s pressure drop at different meshes, frequencies and initial charging pressures

結合圖6、圖7可以看出，各工況下，冷吹過程的壓降均大于熱吹過程。這是因為熱吹時，進入流域內的氣體溫度較高，雖然會增加氣體分子內能，湍流也更為劇烈，但此時氣體密度比冷吹時低很多。

3.3 摩擦特性

圖8為f-Re擬合曲線。由圖8可以看出：在低雷諾數下，二氧化碳氣體工質的流阻系數（黑色曲線）大于空氣工質（Tanaka和Gedeon等人提出的關聯式，分別為紫色和綠色曲線）；隨著雷諾數的升高，二氧化碳氣體流阻系數逐漸接近空氣工質的流阻系數。流阻系數擬合關聯式為：

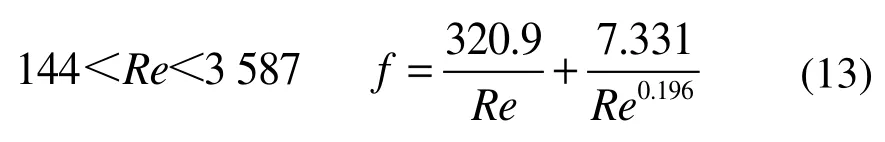
擬合得到的二氧化碳關聯式在雷諾數范圍內與Tanaka提出的關聯式在低雷諾數下（Re＜1 733）相差大于10%，在高雷諾數下（1733＜Re＜3 587）差異小于10%；與Gedeon提出的流阻關聯式最大相差47.3%，最小相差21.7%。根據Liu等人[18]的報告，該現象可以用Darcy-Forchheimer方程來解釋：

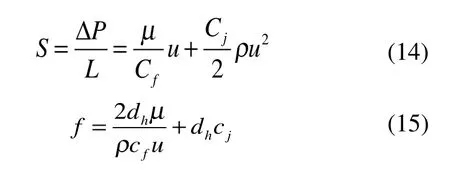
當雷諾數較大時，速度較大，此時氣體物性對摩擦影響較小；但是當雷諾數較小時，速度較小，這時摩擦系數受氣體物性影響較大。因此，二氧化碳和空氣的流阻關聯式在低雷諾數下差異較大而在高雷諾數下差異較小。

由于熱吹和冷吹過程的壓降相差較大（見3.2節），分別對2個過程進行分析，結果如圖8所示。

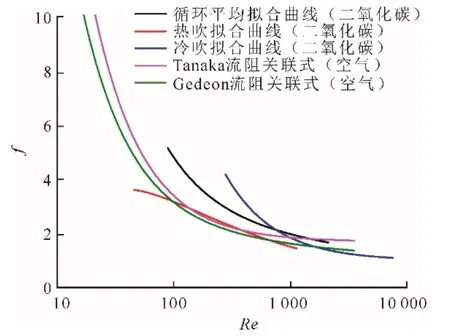
圖8 f-Re擬合曲線Fig.8 The f-Re fitting curves

在雷諾數較小情況下，冷吹階段摩擦系數大于熱吹階段，且差異明顯，在所研究雷諾數Re范圍內（467＜Re＜1 889），二者差異最大和最小分別為79%和32.1%。擬合公式如下：

冷吹過程：467＜Re＜13 361

熱吹過程：75＜Re＜1 889

冷、熱吹過程由于溫度不同，工質黏度和密度變化較大，如圖9所示。因此，冷、熱吹過程的流阻系數存在差異。

3.4 振蕩流模型驗證

將式(13)帶入振蕩流模型（Fluent多孔介質模型），對比相位角為90°和180°的實驗和模擬結果，如圖10所示。由圖10可以看出：相位角為90°時，空氣平均壓降的實驗結果為0.041MPa，模擬結果為0.044 MPa；二氧化碳平均壓降的實驗結果為0.05 MPa，模擬結果為0.052 MPa。同時，實驗和模擬中，所有工況的左、右2個測點所得最大和最小壓力誤差也小于7.3%，實驗曲線存在一點偏移。這是由于，實驗中左、右活塞相位差存在1°~2°誤差，并非完美（達到90°），但在模擬時，左、右2個活塞可以準確設定為90°不變。由此可以認為該振蕩流模型可以運用于研究二氧化碳工質循環率的修正。

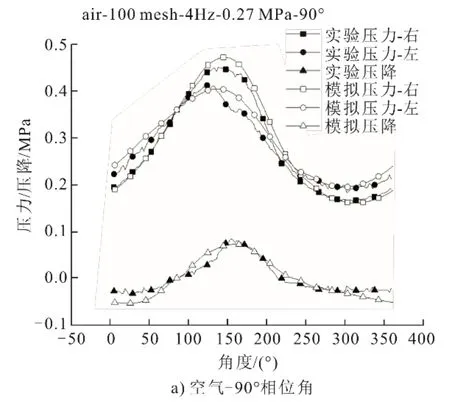
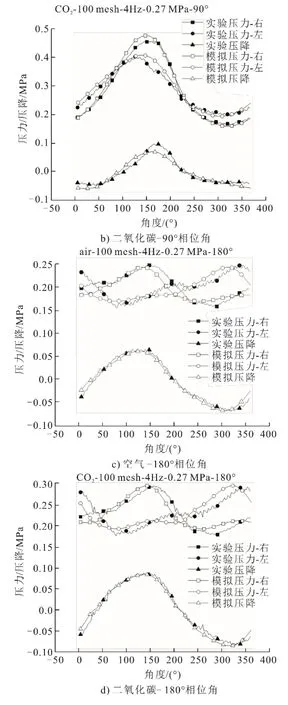
圖10 振蕩流模型驗證Fig.10 The verification result of the oscillation flow model

3.5 循環率修正

在實際設計回熱器時采用的是氣體的理論循環質量，并根據式(18)初步判斷回熱器的孔隙率及外徑或體積[19]：

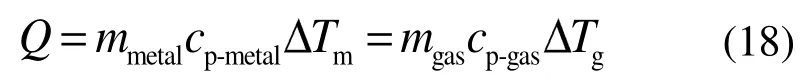
由于存在滯后特性，回熱器中的質量流量和理論質量流量存在差別，在設計時可能導致回熱器能力未能得到充分發揮，同時還增加了流阻損失。因此，利用循環率來討論斯特林發動機不同截面的平均質量流量。通過Fluent得到各截面的瞬時質量流量，然后對各截面1個循環內的質量流量進行積分，得到每個截面的循環質量Mcr，理論循環質量Mct則是根據式(18)計算。再提出循環率（cycle rate）的概念，即各截面的氣體循環質量與理論循環質量之比：

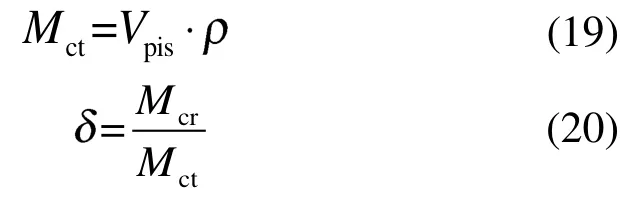
在模型中取了7個截面：左氣缸出口截面、左中心截面、左測試面、回熱器中心面、右測試面、右中心截面和右氣缸出口截面，分別記作截面1、2、3、4、5、6、7（圖5）。

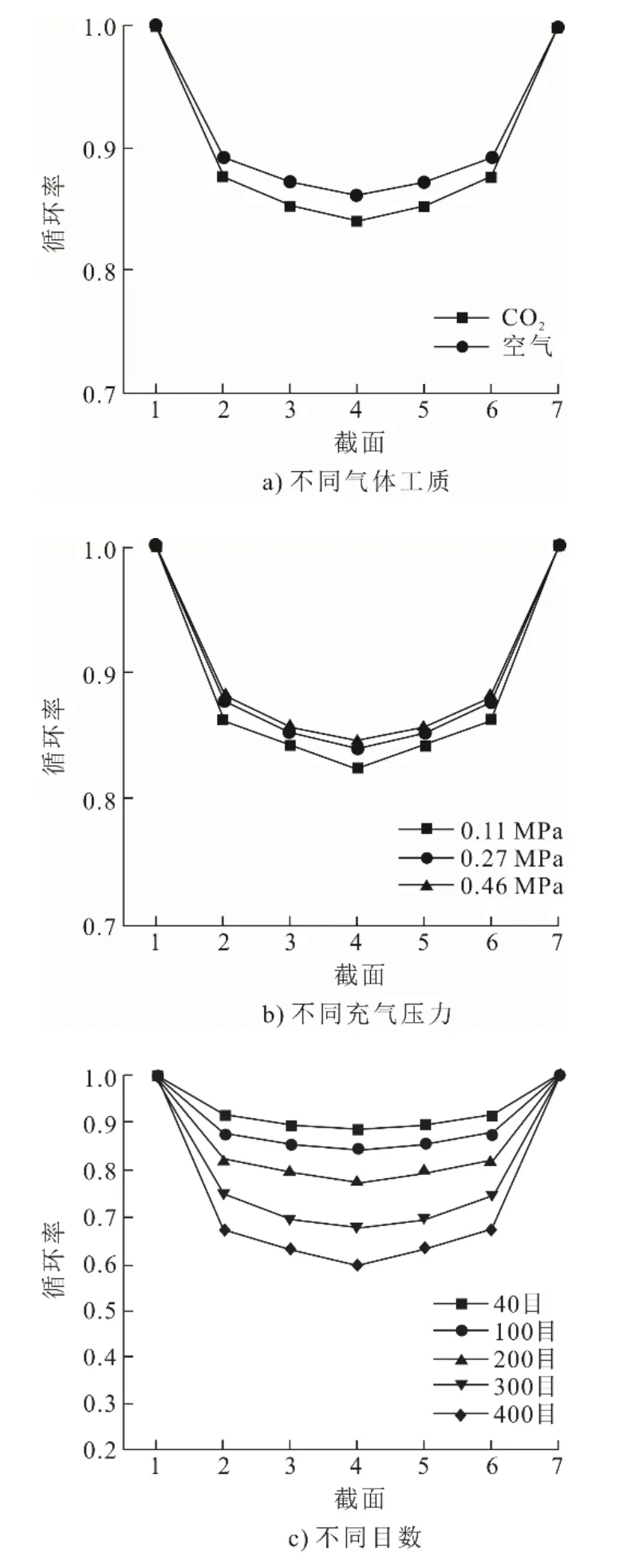
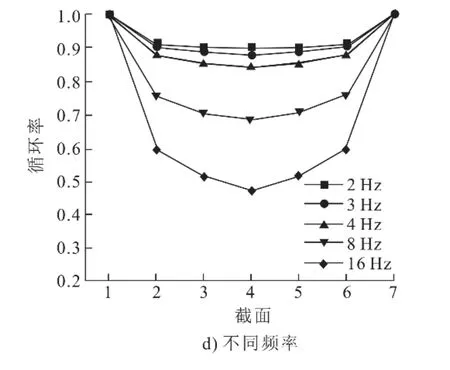
圖11 不同工況下各截面循環率Fig.11 The cycle rate of each section under different working conditions

由圖11a)可以看出，由于各種流阻的存在，循環率無法達到100%，即內部真實進入回熱器的質量流量與設計工況存在區別。在即將進入回熱器之前，空氣和二氧化碳在截面4的循環率分別是86.1%、84.1%，這種現象在不同目數和頻率的工況下更為明顯（圖11c)、圖11d)），200和400目絲網截面4的循環率分別是76.9%、59.4%，3 Hz和16 Hz循環率分別是87.9%和47.2%。

然而，充氣壓力對整體循環率影響十分有限（圖11b)）：充氣壓力為0.11、0.46 MPa時，截面4的循環率僅相差2.3%。

整體來說，該模型循環率分布主要呈現類拋物線形狀，但其最低點出現在截面2附近，這是由于壓縮腔和膨脹腔體積不同，初始位置時兩側活塞到中間回熱器的距離不同。

根據圖1c)和圖11d)中截面4的結果擬合出2個回熱器入口處的循環率為：

（R2=0.997 3，f為頻率）；

在設計斯特林發動機內部回熱器時，可以根據式(21)—(22)對實際的質量流量分布做出更為準確的判斷，設計更為合理的回熱器。

4 結 論

1）壓降與金屬絲網目數、發動機頻率、充氣壓力成正相關；熱端溫度越高，熱吹過程壓降越小，但冷吹過程壓降越大；同時，冷、熱吹過程由于密度不同，其壓降不同。

2）擬合得到了流阻關聯式。由于冷、熱吹過程溫度不同，工質黏度和密度差異和變化較大，2個過程中流阻系數產生差異，建議在冷、熱吹過程采用不同的關聯式，以確保計算結果更為準確可靠。

3）對比二氧化碳與空氣的流阻關聯式后發現，二氧化碳的流阻系數在模擬工況范圍內（144＜Re＜3 587）大于空氣的流阻系數，在雷諾數較低（Re＜1 733）時相差大于10%，但在高雷諾數下（1 733＜Re＜3 587）差異小于10%。

4）獲得了滯后角度回熱器入口處循環率的關聯式，可以將其應用于回熱器設計程序中，進而確定回熱器中真實質量流量，指導基于二氧化碳工質的斯特林發動機設計。