CCD雙軸自準直儀的長距離測量實現

王星星 周小全 呂斌

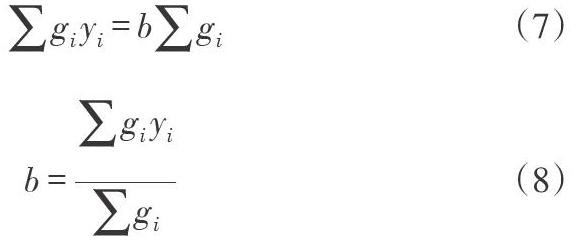
摘 要：本文闡述了一種基于面陣CCD的雙軸自準直儀的長距離測量方法。其間利用上位機對十字叉絲的圖像處理結果與德國ELCOMAT 3000測角真值進行比較，驗證光學系統的測角精度，并采用灰度重心法與最小二乘法相結合的算法，使定位精度達到亞像素級。分析結果顯示，在±10″內測量精度優于0.2″，在±100″內測量精度優于3″。試驗結果表明，該方法具有較高的實用價值。

關鍵詞：面陣CCD;雙軸自準直;長距離測量;亞像素

中圖分類號：TH741.14文獻標識碼：A文章編號：1003-5168（2020）29-0059-03

Abstract： This paper described a long-distance measurement method of a dual-axis autocollimator based on an matrix CCD. In the meantime， the image processing results of the cross hairs by the upper computer were compared with the true value of the German ELCOMAT 3000 angle measurement to verify the angle measurement accuracy of the optical system， and an algorithm combining gray barycentric method and least square method was used to make the positioning accuracy reach the sub-pixel level. The analysis results show that the measurement accuracy is better than 0.2" within ±10"， and the measurement accuracy is better than 3" within ±100". The test results show that this method has high practical value.

Keywords： matrix CCD;dual-axis autocollimator;long-distance measurement;sub pixel

CCD自準直儀是目前測量微小角位移的常用計量精密儀器之一。借助平面反射鏡，通過與細分多齒分度臺相互配合，CCD自準直儀被廣泛用于多面棱體、經緯儀檢定裝置、角度塊等量具的測量[1]。自準直儀具有較高的測量精度和準確度，所以被廣泛應用于精密的測量領域，比如，在導軌的直線度測量、角度測量、軸系的角晃動測量、平板的平面度測量等方面，其發揮著重要的作用。同時，隨著應用領域的不斷擴大，人們開始不僅僅滿足于對自準直儀測量精度及量程等指標的要求，而且在實現長距離測量方面有更多的需求。因此，從事CCD自準直儀長距離測量方面的研究具有重要的實際意義。

1 系統組成及其原理

1.1 CCD自準直儀測角系統

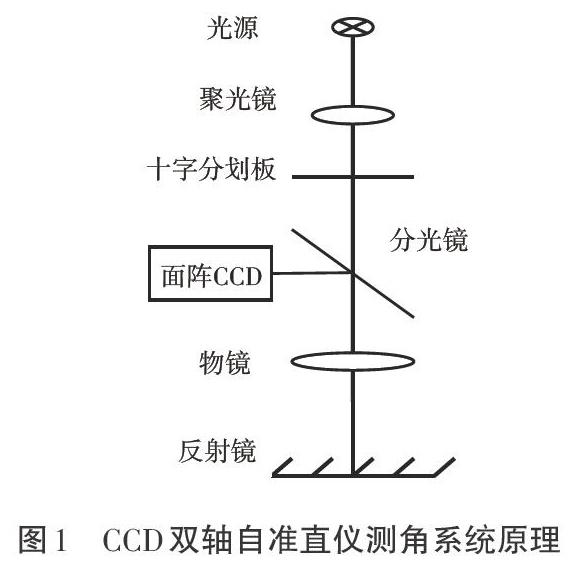
CCD自準直儀測角系統主要由光學機械結構和上位機兩大部分構成，其中光學機械結構由光源、聚光鏡、十字分劃板、分光鏡、物鏡、反射鏡和CCD相機組成，上位機主要實現圖像的采集、數據處理以及實時顯示X與Y軸的角度值等功能。系統原理如圖1所示。

如圖1所示，CCD自準直儀LED發出光源，此光源借助聚光鏡和十字分劃板，最終在平行光管內形成一束平行的十字光源。發出的十字光源與發射鏡面交匯，反射回CCD自準直儀內，由CCD圖像感光芯片記錄發射光信號，通過圖像采集系統將視頻信號傳輸給PC機，由PC機實現圖像信息保存和圖像處理，從而達到計算十字像二維位移的目的。

1.2 測角系統數學模型

由于CCD傳感器芯片設計工藝的限制，它的最小象元尺寸無法滿足現今角度測量精度的實際要求[2]。為此，人們開始關注亞像素分割技術的研究。像素細分的方法有以下幾種：灰度重心法、拋物線擬合法、高斯內插法[3]。本文采用的是灰度重心法與最小二乘法相結合的算法。

十字光源成像到圖像傳感器上時，其為兩條具有一定寬度且相互垂直的交叉線。如圖2所示，圖中[AB]為其中一條直線的中心線，設[AB]的直線方程為：

得到每條光線的中心點后，運用最小二乘法擬合得到兩條光線的中心線，然后利用虛擬出的兩條直線，即可得到其相交點，從而得到十字像的中心位置。

測角光路圖如圖3所示。當反射鏡有微小的角度[θ]移動時，反射光線和入射光線夾角偏移2[θ]，因此像[o′]相對于反射鏡垂直于光軸時的像[o]偏移[x]位移，此時可以得到[x]位移的計算公式為：

式中，[f]為CCD自準直儀的物鏡焦距;[θ]為發射鏡的角度偏移量。

其中，[θ]可以用公式表示為：

分別計算得到[x]、[y]軸的位移偏移量，通過式（10）即可得到發射鏡面相對[x]、[y]軸的角度偏移量，從而達到[x]、[y]雙軸角度測量的目的。

2 試驗結果及誤差分析

目前，可用于自準直儀的光電轉換器件主要有面陣CCD、線陣CCD、四象限光電探測器、PSD四種[4]。本文采用的是基于面陣CCD的光電轉換器件，分辨率為1 296×966，像元尺寸為3.75 μm×3.75 μm。

平行光管是第一層傳感，把幾何量的變化轉化為平行光管中十字分化線位置的變化;CCD攝像機把十字分化線位置圖像信息變成視頻模擬信號;圖像采集卡在驅動程序的作用下把CCD攝像機的視頻模擬信號變成數字圖像信息;數字圖像信息經過計算機系統的處理（包括圖像的預處理、二值化、微分、擬合及細分），圖4表示的是反射鏡離光管15 m處CCD相機獲取的十字像。顯然，隨著測量距離的增加，獲取的十字像的尺寸逐漸變小，而且光叉絲的寬度隨之變細，這點是CCD自準直儀實現長距離的難點之一。

由于德國穆勒公司生產的EL COMAT 3000自準直儀的測量精度較高，筆者利用新設計的遠距離自準直儀與穆勒光電自準直儀進行了比對試驗，表1是二者間距為15 m時的測量結果。其間，焦距f為300 mm。

由于篇幅的關系，表1只列舉了負方向上的測量角度。從表1可看出，研制的CCD雙軸自準直儀可以測量到-200″。為了直觀地顯示自準直儀的測量效果，利用MATLAB軟件對表1數據進行處理，圖5表示試驗之后得到的穆勒自準直儀和試驗樣機的測量結果以及誤差。其中，Bastler2表示的是試驗樣機測量結果。

從圖5可以看出，在15 m測量距離時，除個別點外，試驗樣機在10″范圍內的測量誤差優于0.2″，在100″測量范圍內誤差優于3″，同時，隨著測量角度的增加，試驗樣機相對穆勒光電自準直儀的測量誤差增大。

3 結語

本文介紹了一種CCD雙軸自準直儀實現長距離測量的方法，并建立了基于灰度值重心法和最小二乘法相結合算法的亞像素分割數學模型，得到了在15 m測量距離時自準直儀樣機的測量精度及量程。該光學系統結構簡單，采用角度測量算法，其在Visual C++編程軟件中易于實現。

參考文獻：

[1]鄒九貴，甘俊紅，季國定.高精度二維自準直儀的研制[J].新技術與新儀器，2006（5）：19-26.

[2]鄭友琴，袁旭軍.用CCD實現精密長度測量[J].電測與儀表，1998（35）：45-47.

[3]王雯倩，劉國棟，浦昭邦，等.利用面陣CCD測量小角度的研究[J].光電技術應用，2004（2）：134-138.

[4]黃偉成.基于線陣CCD的邊緣測量及重構技術的研究[D].武漢：武漢理工大學，2008.