基于灰色關聯分析和PSO 改進的多變量GM（1，N）模型*

李克文 李 萍

（中國石油大學計算機與通信工程學院 青島 266580）

1 引言

長期以來，許多學者對預測理論進行了廣泛深入的研究，并提出一系列預測方法，如時間序列法、人工神經網絡法、支持向量機法、灰色預測法等［1～2］，這些方法大多采用單變量建模和預測，不能充分考慮變量之間作為整體存在時的相互影響［3］，且在預測過程中需要大量可靠地預測數據作為支撐。隨著研究的深入，一些學者提出多變量灰度預測模型，也稱為GM（1，N）模型，灰色預測模型是灰色系統理論中最重要的組成部分之一，通過對“部分”已知信息的分析，提取有價值的信息，實現對數據變化規律的正確描述和有效預測［4］。

對灰度預測模型的改進研究一直是近年的熱點［5～6］：通過改進初始條件或利用智能算法獲取更為合適的背景值［7～8］，從而獲取更為準確的預測效果。GM（1，N）模型的結構比單變量灰色預測模型復雜，建模過程充分考慮了相關因素對系統變化的影響［9～10］，但GM（1，N）模型存在建模機制和模型結構上存在不足，因此在實際應用中常常導致模型誤差大于GM（1，1）模型。為了提高GM（1，N）模型的仿真和預測性能，Tien 優化了傳統GM（1，N）模型的結構，在該領域發揮了重要作用［11］；Wang等通過引入控制參數和插值系數，提出了一種基于卷積積分的GMC（1，N）優化模型［12］；Zeng等提出了一種新的OGM（1，N）模型，解決了傳統GM（1，N）模型的建模機理、參數估計和模型結構的缺陷問題［13］。本文在OGM（1，N）基礎上，以模型還原值和實際值的誤差平方和最小化為目標，提出一種基于灰色關聯分析和PSO算法的多元變量灰度預測模型，通過灰色關聯度計算獲取與參考序列變化密切相關的自變量序列，基于PSO 算法改進模型初始條件，在N = 1 和N ＞1 兩種情況下分別對模型進行建模預測和發展系數求解優化，降低模型范圍，從而提高了改進模型的預測精度和適用范圍。

2 OGM（1，N）模型建模原理

通過研究發現，GM（1，N）模型存在一些嚴重的缺陷［13］：1）作為一個有N個變量和一個一階方程的灰色預測模型，當N =1 時，現有的GM（1，N）模型不能轉化為相應的GM（1，1）模型，這說明GM（1，N）模型的結構存在一定的缺陷；2）GM（1，N）模型的最終時間響應表達式是通過一個理想的簡化過程得到的，這可能會導致GM（1，N）模型的不穩定性；3）參數估計與參數應用的錯位是傳統GM（1，N）模型的第三個缺陷。針對GM（1，N）模型現有的建模機理、參數估計和模型結構三個方面的嚴重缺陷，Zeng 等引入線性修正項h1（k-1）和灰色作用量項h2，提出了一種新的灰色優化模型OGM（1，N）［13］，解決了傳統GM（1，N）模型的三個缺陷，其建模過程如下：

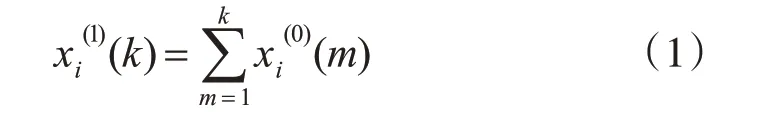
其中i=1，2，…，n，k=1，2，…，p。

2）由Xi（1）生成緊鄰均值序列Z（1）＝｛z1（1）（k）｝（k=1，2，3，…，p）。

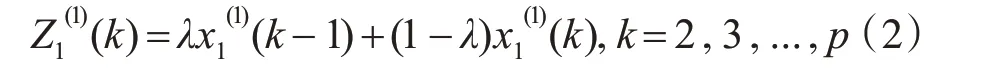
其中，背景值λ 默認為0.5。假定X（1）具有近似指數變化規律，數列X2（1），X3（1），…，Xn（1）對X1（1）的變化率產生影響，則Xi（1）序列滿足下述的一階線性微分方程：

這個微分方程模型記為GM（1，N），將上式離散化，并引入線性修正項h1（k-1）和灰色作用量項h2，得到OGM（1，N）灰微分方程如下：

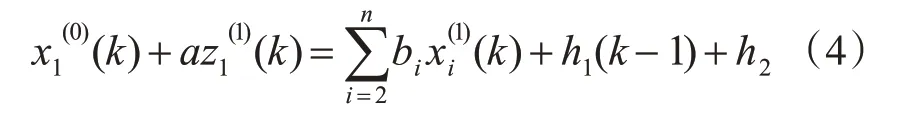
記式（4）的離散形式如下：

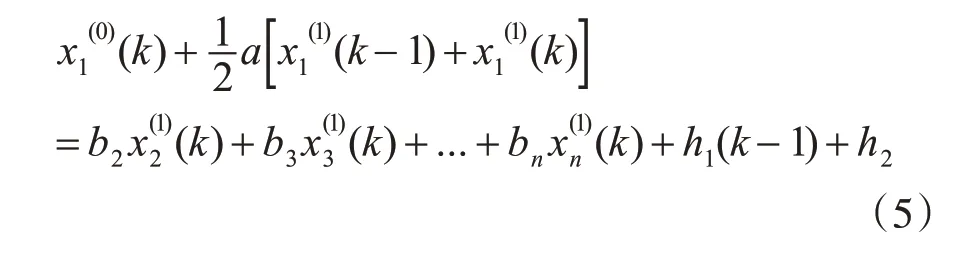
其中，k=2，3，…，p，a 為系統的發展系數，bi為驅動系數，線性校正項h1（k-1）反映了因變量和獨立變量之間的線性關系；灰色作用量項h2表示因變量序列中的數據變化關系。要求解此微分方程，須先確定參數a、bi、h1、h2。

3）利用最小二乘法求得參數a、bi、h1、h2的值：

其中：

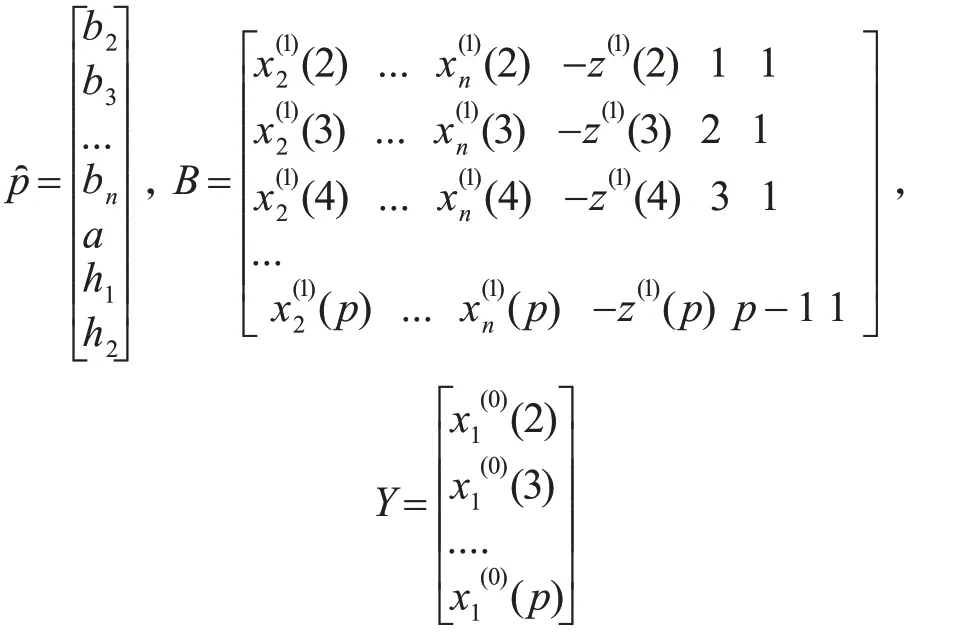
4）將a、bi、h1、h2的值帶入式（5）解微分方程，得其離散解為

其中：

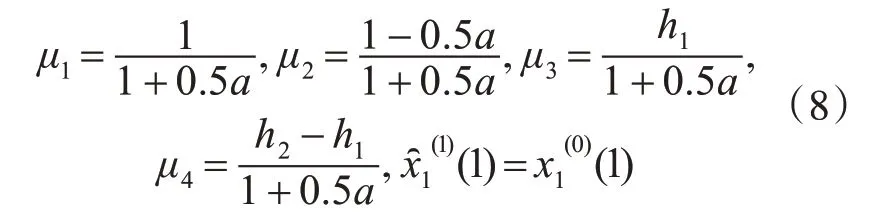
5）對式（7）做一次累減還原運算，得到原始序列X1（0）的灰色預測值：

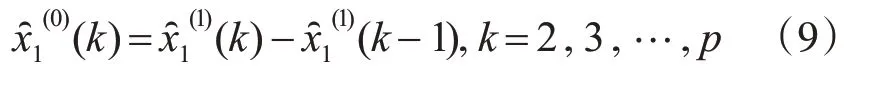
3 基于灰色關聯分析和PSO 對OGM（1，N）模型的改進

本文在OGM（1，N）模型的基礎上，通過灰色關聯分析法評估各個因素與預測數據的關聯程度，從而挖掘出對預測數據影響較大的因素組成自變量序列，作為灰度預測模型的輸入，另外，針對OGM（1，N）建模過程中的參數估計問題，利用PSO 算法分別在N=1和N ＞1兩種情況下對模型中a、bi、h1、h2值進行求解優化，避免直接定義背景值λ=0.5，再對a，b 值進行求解產生的雙重誤差，使模型誤差最小化。

3.1 基于灰色關聯分析的選擇

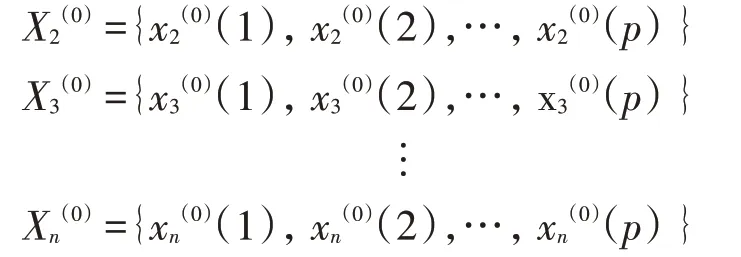
作為比較數據序列，是影響系統行為的因素。

2）確定每個數據序列中的最大值和最小值，針對參考數列和比較數列進行無量綱化處理：

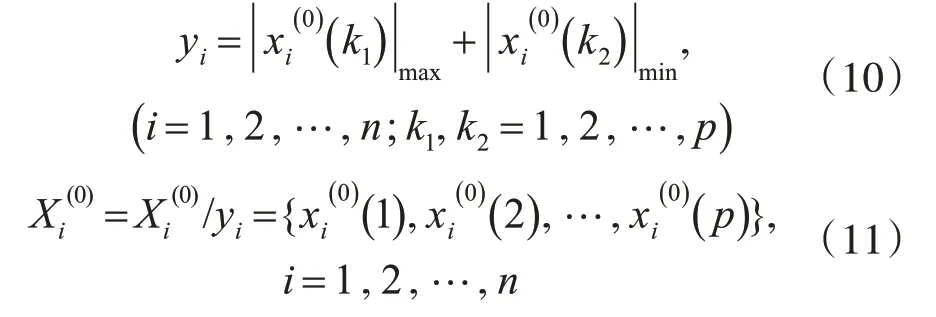
3）計算比較數列xi和參考數列x1在第k個指標上的灰色關聯系數：

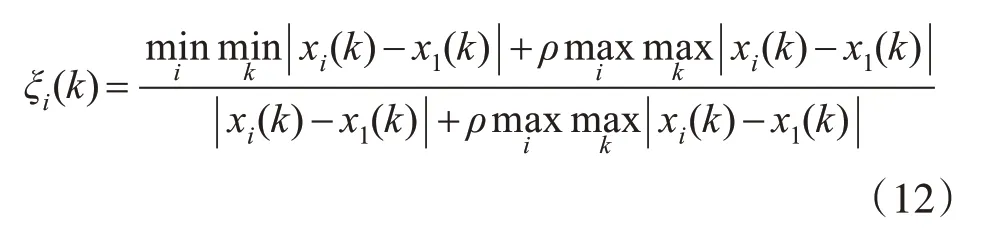
4）計算灰色關聯度γi：

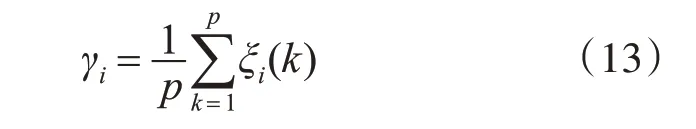
設置關聯度閾值γ0=0.6，提取｛γi|γi＞γ0｝的特征屬性集組成新的自變量數據序列Xi'（0）=｛xi'（0）（1），xi'（0）（2），…，xi'（0）（p'）｝，i=1，2，…，n，為方便后續表達，將Xi（'0）記為新的X（i0）。

3.2 基于粒子群算法對OGM（1，N）模型的改進

根據變量參數N 的大小，采用粒子群算法對具體參數進行優化求解，最小化模型誤差。POGM（1，N）建模過程如下：

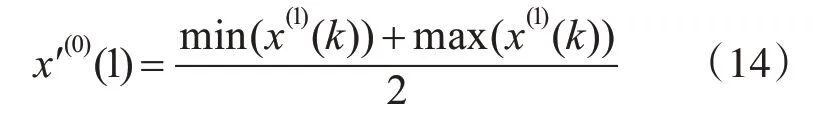
2）I.當N = 1 時，令h1=0，將OGM（1，N）模型轉換為GM（1，1）模型：

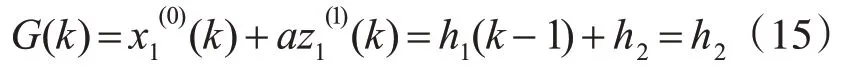
由G（k+1）-G（k）可得：

又根據GM（1，1）模型原理可得：

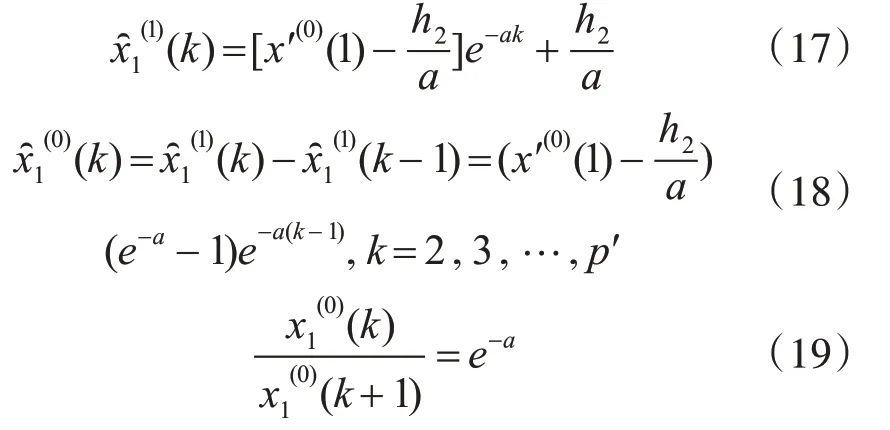
聯立式（16）、（19）可得，

（1）初始化一個規模為m（m ≥4）的粒子群，設定初始位置向量ai=（ai1，ai2，ai3，…，aim），h2i=（h2i1，h2i2，h2i3，…，h2im）和初始速度向量Vi=（vi1，vi2，vi3，…，vim），因為在實際運用過程中a 的取值不會超過0.5［15］，所以：

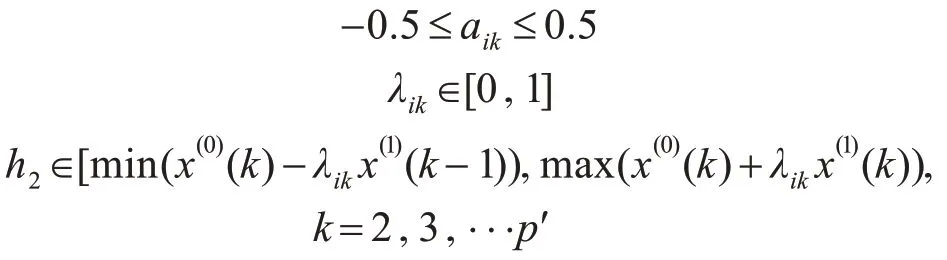
（2）將a，h2的值代入式（18），求得：

II.當N ＞1時，OGM（1，N）模型如下所示：

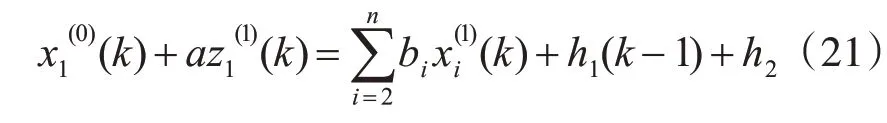
（1）初始化一個規模為m 的粒子群，設定初始位置向量λi=（λi1，λi2，λi3，…，λim）和初始速度向量Vi=（vi1，vi2，vi3，…，vim），每當給定一組li，PSO 調用OGM（1，N）模型文件即可獲得一組對應參數解：［b2，b3，…，bn，a，h1，h2］i，根據實際運用過程［15］，參數解須滿足以下條件：

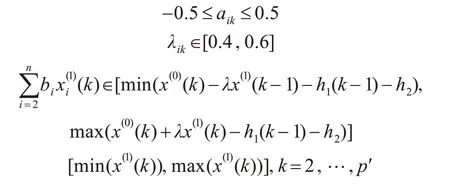
（2）將a，bi，h1，h2的值代入式（7）、（8）、（9），求得

3）計算每個粒子的適應度值，取適應度函數為

4）比較每個粒子的適應值fmin和其經歷過的個體 最 優 位 置pbest 的 適 應 值fpbest，若fmin＜fpbest則 更 新fpbest=fmin；

5）比較每個粒子的適應值fmin與其經歷過的全局最優位置gbest 的適應值fgbest，若fmin＜fgbest則更新fgbest=fmin；

6）在找到這兩個極值后，根據粒子的速度、位置進化方程來更新粒子；

7）如果滿足終止條件，則輸出解，否則返回3）繼續循環查找。

4 改進的灰色模型在數據預測中的應用

本文基于文獻［13］中的抗拉強度數據集和文獻［3］中的基坑監測數據集進行實驗分析，具體實驗數據如表1、表2所示。在實驗數據的基礎上，取ρ=0.05，根據3.1 節中的灰色關聯分析法分別對表1、表2 數據集的三組數據序列進行灰色關聯度計算，計算結果如表3 所示，γ12，γ13均大于0.7（最常用的臨界值為0.6），說明三組數據序列之間相互關聯，兩個數據集均可以作為預測模型的輸入。

表1 抗拉強度數據集

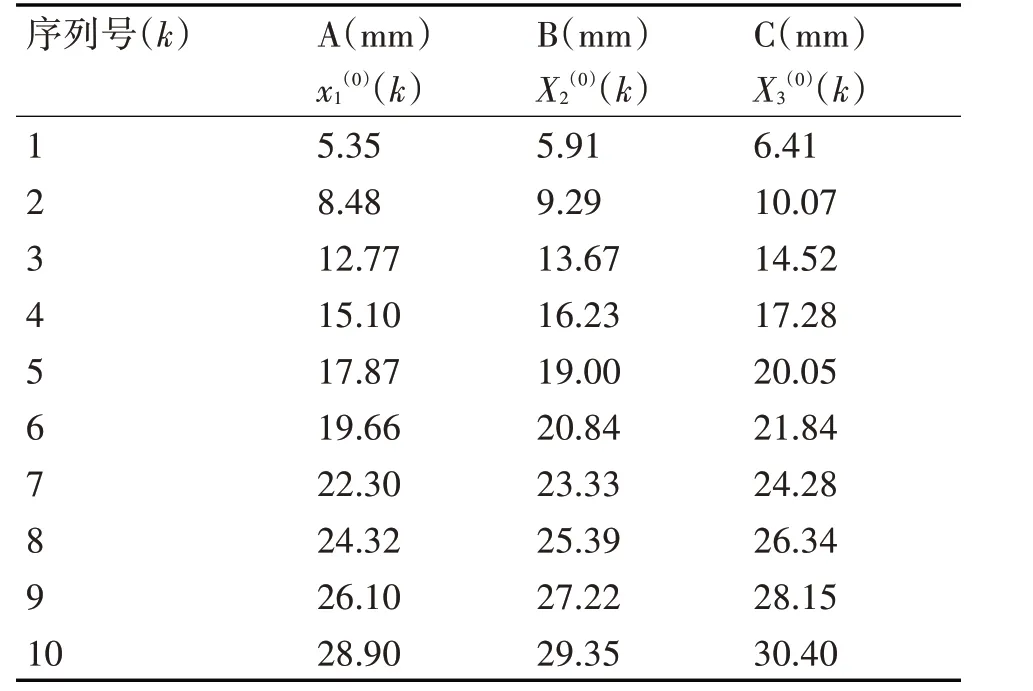
表2 基坑監測數據集

表3 基坑監測數據

為了全面驗證POGM（1，N）模型效果的有效性，本文在Matlab 平臺上進行實驗，分別將表1、表2 數據集的前六個序列根據3.2 節中基于PSO 優化的OGM（1，N）模型（簡稱為POGM（1，N）模型）、GM（1，1）模型、GM（1，N）模型和OGM（1，N）模型進行建模，預測下一個序列，同時刪除第一個序列，增加最新數據序列作為輸入，繼續向后進行預測，并且采用平均絕對誤差、均方誤差、平均百分比誤差作為預測結果評判標準，計算過程如式（10）～（12）所示［16］，預測結果對比圖如圖1、圖2所示。

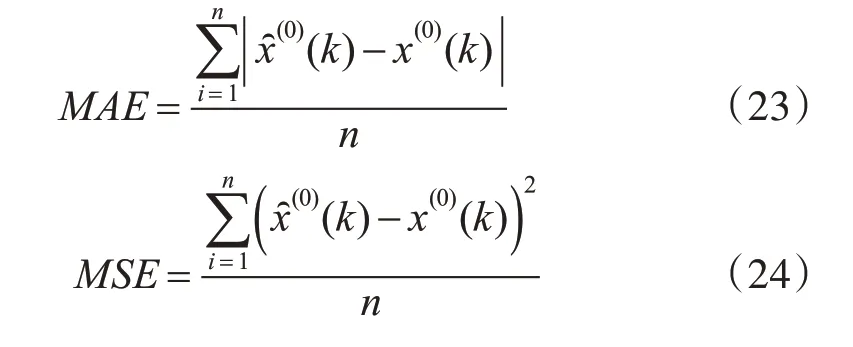
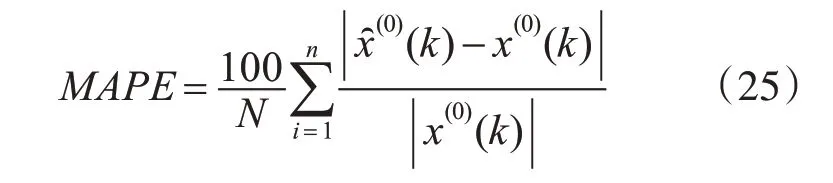
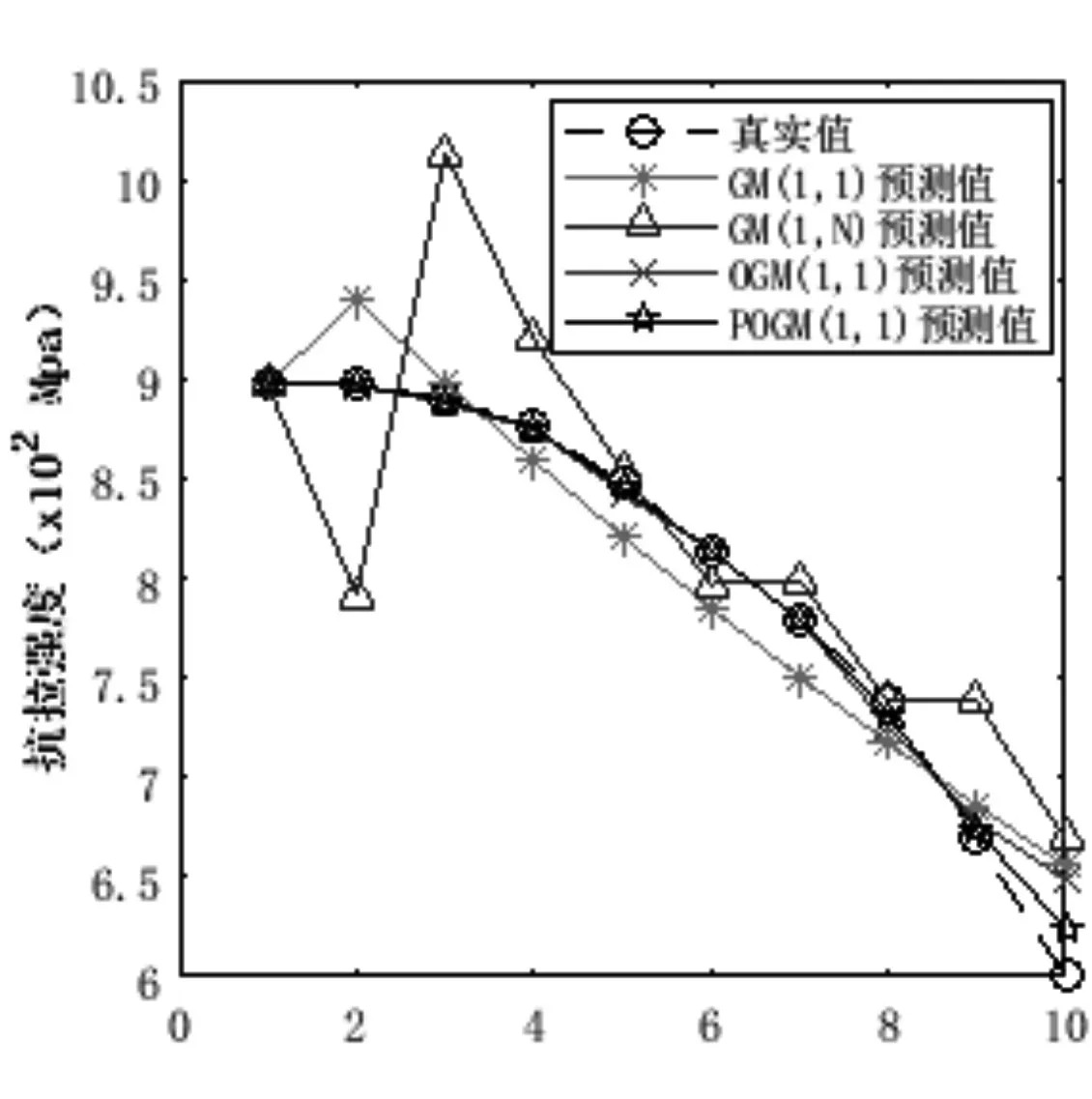
圖1 各模型預測結果對比圖

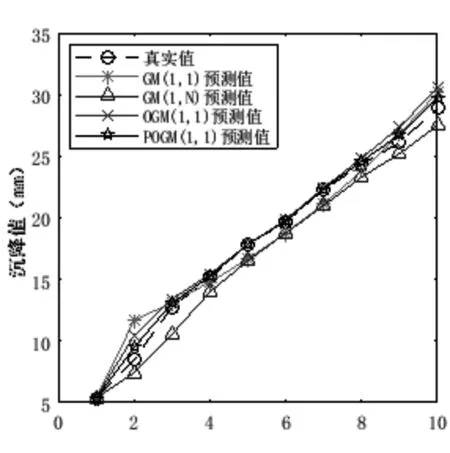
圖2 各模型預測結果對比圖

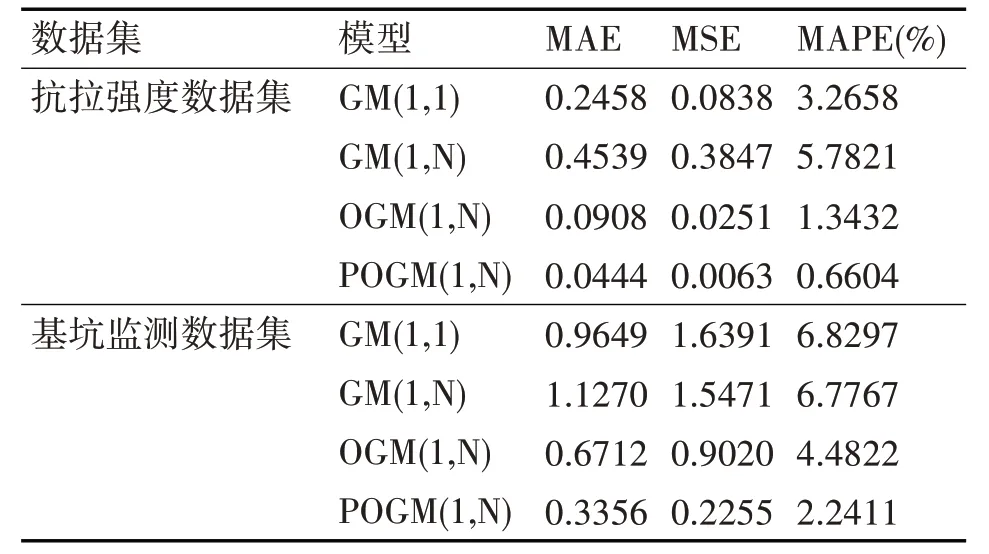
表4 各模型性能對比

從圖1 可以發現，在抗拉強度數據集上，GM（1，N）模型預測過程出現較大偏差，GM（1，1）模型除個別點出現較大偏離外，絕大多數點誤差相對較小，但GM（1，1）模型沒有準確反映出真實數據的變化趨勢，POGM（1，N）模型和OGM（1，N）模型充分考慮了數據點之間的變化趨勢，預測結果相對穩定。從圖2 可以發現，在基坑監測數據集上，傳統GM（1，1）模型和GM（1，N）模型的預測結果相對穩定但是誤差較大，POGM（1，N）模型和OGM（1，N）模型預測結果更接近于真實值，絕大多數點相對誤差較小，預測結果更為穩定。另外，通過表4 中各個模型在表1、表2 數據集上的預測指標對比可以看出，本文所提方法在MAE、MSE 和MAPE 三大指標下的性能相對于GM（1，1）模型、GM（1，N）模型有了較大提升，和OGM（1，N）模型相比，在MAE、MSE 和MAPE 指標上分別下降了0.0464，0.0188，0.6828%和0.3356，0.6765，2.2411%。這說明，本文所提出的POGM（1，N）模型能獲得比其他方法更好的預測效果，POGM（1，N）模型預測精度高，更能反映數據的真實變化趨勢。

5 結語

本文提出了一種基于粒子群優化算法進行參數尋優求解的GM（1，N）優化模型，該模型采用灰色關聯分析法計算提取與參考序列關聯度值較高的序列，組成模型的自變量輸入序列，并在OGM（1，N）模型的預測原理上優化模型初始條件，根據PSO 算法進行多元變量灰度模型的參數尋優和預測建模，借鑒滑動窗口的思想，依次向后進行序列預測，有效提高了改進模型的適用范圍。通過在基坑監測數據集和抗拉強度數據集上的實驗，證明了改進模型具有較高的預測精度。