考慮負載平衡的科學工作流容錯聚類算法研究

高瑋軍，張春霞，楊 杰，師 陽

蘭州理工大學 計算機與通信學院，蘭州 730050

1 引言

科學工作流為科學研究提供了一種流程定義和自動運行的平臺，可以屏蔽底層繁瑣的計算過程以此簡化科學實驗。科研人員只需關注專業問題的處理，從而使得科學實驗能夠更便捷、高效地進行。在科學研究領域，例如：生物基因學、天文學、物理學、地震學等大規模應用中，工作流包含許多細粒度計算任務，任務間存在復雜的依賴關系。這些任務通常只需要幾秒鐘或幾分鐘的執行時間，任務實際執行時間可能比系統開銷（系統中除執行用戶計算以外的其他開銷）更短[1]。系統開銷是分布式計算中普遍存在的問題，也是科學工作流應用程序的性能可以顯著提升的主要原因[2]。隨著網格計算、云計算等分布式環境的出現和硬件設備的優化，系統開銷問題更加凸顯，嚴重影響了科學工作流的執行效率。

任務聚類方法對具有某一特征的任務進行聚集生成聚類，系統以類為單位進行調度。該方法雖然增加了作業運行耗時，但是顯著地降低了系統的總開銷[3]。文獻[4]結合計算任務劃分技術與任務聚類，解決了數據密集型地震模擬工作流（CyberShake）在求解時間方面所面臨的問題。細粒度任務的低性能問題在廣泛使用的分布式平臺中更加凸顯，其中資源的調度開銷和隊列等待占用的時間較長。文獻[5]為了減少工作流的總運行時間和云資源使用，提出了一種基于任務分組和復制技術的調度算法，來降低用戶執行成本。針對跨地域跨學科的科學研究工作中，普遍存在數據傳輸開銷嚴重影響系統運行效率的問題，任務聚類方法被用于數據放置策略和資源調度策略中[6]，以減少數據傳輸所產生的時間開銷。科學工作流執行過程中存在故障風險，而大部分任務聚類算法及其優化算法并未考慮故障對系統的影響。

在任務聚類算法執行后，工作流系統以類為基本單位進行調度和執行，類中有一個任務失敗，整個類被標記為失敗。解決任務失敗問題最常用的方法是重試失敗的作業、備份技術、設置檢查點[7-9]。對于運行周期比較長的作業，備份技術會造成嚴重的資源浪費。為了減少資源浪費，可以按周期檢查作業執行情況，以限制重試的任務量。由于檢查點機制實現相對重試技術較為復雜，執行檢查點的開銷會同樣會限制系統的運行效率。Chen等人[10]針對瞬時故障提問題提出了任務/作業故障模型，并提出了動態重聚類算法（DR）。隨后又提出了三種任務容錯聚類方法，可以有效地解決任務失敗的問題[11]。文獻[12]提出了一種新的基于簇的異構最早完成時間（CHEFT）的啟發式算法，利用資源預配置后的空閑時間運行已失敗的任務，來增強云環境中科學工作流的容錯機制。文獻[13]對現有的云平臺容錯機制進行分析，對科學工作流應用程序中出現的特定故障，討論和推薦解決故障的容錯方法和容錯模型。現有的容錯聚類算法忽略了聚類可能會導致負載不平衡問題[14-15]，這種不平衡會導致下一層任務的釋放延遲，系統的總運行時間也會隨之增加。

工作流分解是處理負載不平衡的常用技術[16-17]，該方法將科學工作流劃分成多個子工作流，子工作流可以高效地并行執行。但是對工作流進行分割會增加中間數據管理開銷，同時，可以進行分割的工作流種類也比較受限。文獻[18]提出了一種基于路徑平衡的費用優化算法，能夠有效地增大了費用優化空間。文獻[19]提出了三種衡量指標來量化描述不平衡問題，根據運行時間不平衡、依賴關系不平衡、位置關系不平衡提出了三種平衡聚類算法，有效縮短了系統總運行時間。

容錯聚類算法在有效解決故障問題的同時，也面臨著負載不平衡問題，本文結合水平運行時間平衡策略與現有的容錯聚類算法，提出了一種平衡重聚類算法。通過平衡聚類的運行時間以實現負載平衡，在提高系統運行效率的同時保證系統的健壯性。

2 定義與基礎理論

2.1 動態重聚類（DR）

負載不平衡：在不考慮任務運行時間存在差異的情況下將科學工作流中多個任務合并為一個聚類，可能會導致聚類的之間的運行時間差異較大，造成虛擬機運行時間嚴重不平衡。

如圖1 所示，任務 t 1，t2，t3 和 t 4 為相互獨立的任務，其中t1，t2，t3，t4 的任務運行時間分別是10 s，10 s，30 s，30 s。

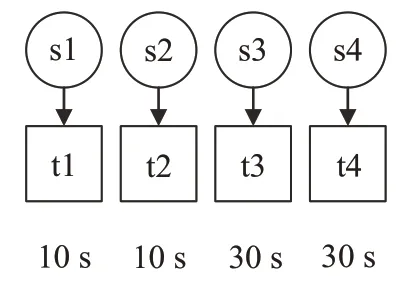
圖1 初始任務集

當有兩個聚類時，水平聚類（HC）方法運行結果如圖2 所示，將任務t1 和任務t2 合并為聚類J1，將任務t3和任務t4聚為J2。則聚類J1的運行時間為20 s，聚類J2的運行時間為60 s，聚類J1 和J2 的運行時間嚴重不平衡。由于下一層任務釋放的必須等待上一層所有任務運行完成，即在60 s后下一層的任務才可以釋放。

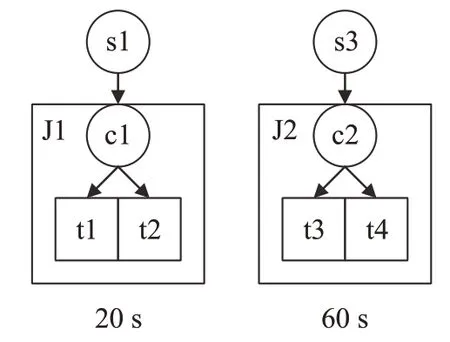
圖2 水平聚類

負載不平衡衡量指標：本文采用水平運行時間方差（Horizontal Runtime Variance，HRV）來描述運行時間不平衡問題。HRV描述了一組任務或作業運行時間的差異大小，HRV定義如下：

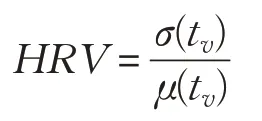
HRV 表示在同一水平層中所有任務/聚類運行時間的方差。公式中分子σ(tv)為所有任務/聚類運行時間的標準差，μ(tv)為該層中任務/聚類運行時間的平均值。在μ(tv)相同的情況下，σ(tv)的值越大，HRV 的值也越大。

初始任務集圖1中，μ(tv)=20 則：

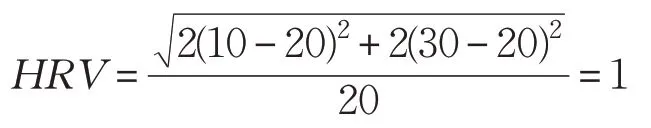
由于科學工作流任務間存在依賴關系，下一層作業的釋放時間取決于上一層任務中最長運行時間。如圖2，HC算法運行后，μ(tv)=40 得：

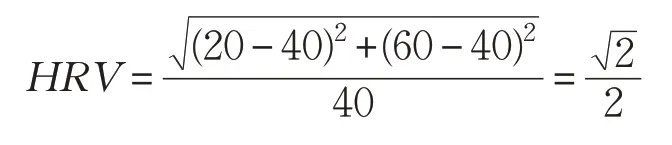
水平運行時間平衡衡聚類（HRB）算法根據任務運行時間的差異進行聚類操作，如圖3 所示，運行時間較長的任務t3 和運行時間較短的任務t1 合并至一個聚類中，任務t4 和任務t2 合并至一個聚類中。聚類J1 和J2的運行時間都為40 s，下一層任務的釋放將在40 s后，計算可得：μ(tv)=40，

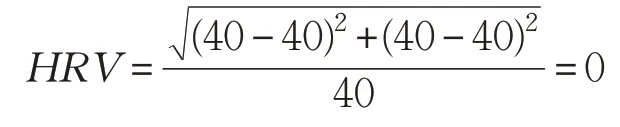
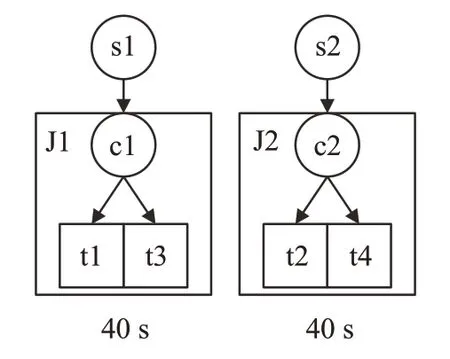
圖3 水平運行時間平衡聚類

對比HC 算法在60 s 后釋放下一層任務，水平運行時間平衡聚類算法（HRB）將在30 s后釋放下一層任務，HRB 算法明顯優于HC 算法。較高的HRV 值意味著下一層任務的釋放較遲。因此，為了提高運行性能，減少作業運行時間方差很有意義。

2.2 容錯機制

在科學工作流執行過程中，故障頻繁發生，嚴重影響科學研究工作。工作流管理系統為工作流執行提供軟件環境，主要負責工作流的定義和管理。科學工作流管理系統中的容錯機制主要用于解決科學工作流流程組合結構設計異常等問題，主要有以下幾種：（1）基于其他任務技術。其他任務是指當前任務的另外一種實現方式，如果流程中正在運行的任務出現錯誤，則啟動另外一種實現方式。（2）備份技術。為全部工作流任務創建多個備份，并將備份任務分配至在不同數據節點上運行，類似于Hadoop 中的文件存儲系統。多個備份任務將同步執行，一旦故障發生，直接調用備份任務代替原任務繼續運行。（3）修復工作流方式。在工作流第一次運行時，科學工作流管理系統記錄下執行過程中間所產生的錯誤信息，然后根據記錄數據，修正工作流組件組合方式和運行參數，經過多次運行和修改，故障率可以大幅度降低。（4）用戶自定義異常處理。用戶擁有一定權限，可以根據自己的需求根據經驗，按照自己的意愿設計錯誤處理方案。

流程級的容錯機制，大多以流程為單位進行容錯，其他任務技術、副本技術都對資源和成本浪費較為嚴重，而修復工作流對于執行次數少或者初次執行的科學工作流，執行效率太低。所以研究人員開發了一系列任務級容錯技術，用于科學工作流調度和執行階段的故障恢復，細化了故障恢復單元，降低故障恢復成本。任務級容錯主要包括：重試技術、副本技術以及檢查點技術。其中，Chen等人[10-11]對科學工作流中故障問題進行了深入的研究，所提出的重聚類算法，重新運行發生故障的任務，改變了傳統的重試技術重新運行所有任務的模式。重聚類算法在有效避免重試技術和備份技術所造成的資源浪費的同時，考慮聚類數量等方面的優化，很大程度地提高了科學工作流系統的運行效率。

科學工作流通常需要大量復雜的分析和計算，相對其他類型工作流故障概率更高。并且科學工作流任務之間存在很強的約束關系，如果其中一個任務發生故障，則與其有依賴關系的所有后續任務都需要重新執行。這表明故障發生后，故障恢復規模較大。為了能夠提高重聚類算法性能，減少任務故障所帶來的損失。本文從負載不平衡角度，研究對重聚類算法進行改進，提出了平衡重聚類算法（BR），在任務調度和執行階段進行故障恢復。

2.3 故障模型

故障的產生具有隨機性和不確定性，因此需要根據歷史數據對故障的產生進行建模，通過故障模型評估容錯算法。在文獻[1]中已經證明系統開銷可以用Gamma分布或者Weibull 分布來描述。Schroeder 和Gibson 已經證實[20]，任務失敗的到達間隔時間更符合Weibull 分布（由形狀參數0.78定義）。文獻[21]中指出，Weibull分布、Gamma分布和Lognormal分布是估計一組工作流任務運行時間的最佳選擇。在本文中，采用Gamma 分布模擬任務運行時間(t)和系統開銷(S)，采用Weibull 分布模擬故障間隔到達時間(u)。

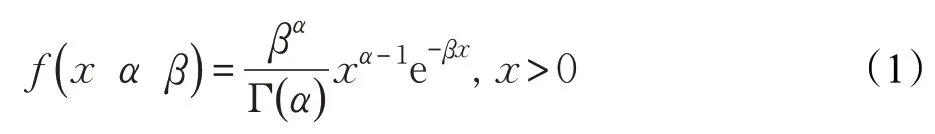
Gamma如公式（1）所示，Gamma分布通常使用兩個參數描述：形狀參數(α)和比例參數(β)。形狀參數決定分布的形狀，比例參數決定分布的拉伸或收縮。Weibull分布是可靠性分析和壽命檢驗的理論基礎，Weibull 分布形式與Gamma分布相似，α表示形狀參數，β表示比例參數。

已知a、b為先驗知識，D為觀測數據，β為目標估計參數。由貝葉斯概率論可知，當觀測數據集已知時β的后驗分布定義如下：

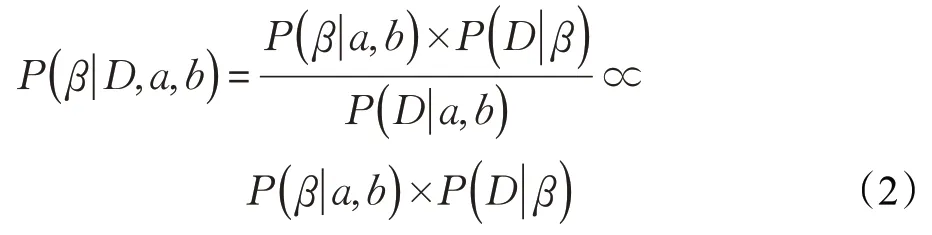
公式中的D可以代表失誤間隔時間(u)、任務運行時間(t)或者系統開銷(S)的觀測值。P(β|a,b)是已知的先驗知識，P(β|D,a,b)是需要計算的后驗概率。定義失誤到達間隔時間u的觀測值為X={x1,x2,…,xn} ；任務運行時間t的觀測值表示為RT={t1,t2,…,tn} ，采用S={s1,s2,…,sn} 表示系統開銷S的觀測值。通過已有的觀測參數，可以得到β的估計值。

使用Weibull 分布來建模失誤到達時間間隔u，其中參數α為已知形式參數（由經驗值給出），只需要計算規模參數β。具有已知形狀參數α的Weibull分布與逆Gamma 分布為共軛對，這表明如果先驗分布遵循逆Gamma 分布，形狀參數為a，比例參數為b，則后驗分布服從逆Gamma分布，形式如下：

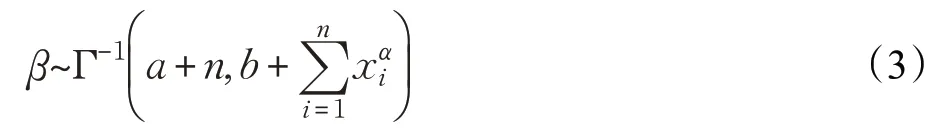
對比例參數β進行最大似然估計估計，β的估計定義如下：

通過相同的步驟，對總運行時間T、系統開銷S以及故障到達時間u等需要提前預知的參數進行估計，從而建立任務故障模型。通過調整故障模型中故障到達間隔時間（故障出現頻率），對所提出的算法進行測試。

3 容錯聚類算法

3.1 選擇重聚類（SR）

選擇重聚類算法在作業運行結束后，輸入標記運行失敗的聚類作業，篩選出作業中運行失敗的任務，并將這些任務合并到新的群集中，提交至主機再次執行。算法1為選擇重聚類算法的偽代碼。

算法1選擇重聚類

輸入：W，科學工作流；C，每個類中的任務數量

輸出：W，科學工作流

1.procedureRECLUSTERING（J）

2.TL←divideAtLeve（lJ）

3.Jnew←{ }

4.forTask∈TLdo

5. iftis failed then

6.Jnew.add(t)

7. end if

8.end for

9.W=W-Jnew

10.returnW

11.end procedure

3.2 動態重聚類（DR）

動態重聚算法對選擇重聚類算法進行改進，考慮聚類規模（聚類中任務數量）對故障的影響。根據故障到達時間間隔、任務規模動態地估計出使得系統開銷可以取到最小的聚類任務數量(K)，在每次重運行時，動態更新K值，根據K值進行聚類劃分。動態重聚類算法的偽代碼如算法2所示。

算法2動態重聚類

輸入：W，科學工作流；C，每個類中任務的數量

輸出：W，科學工作流

1.procedureRECLUSTERING（J）

2.TL←DivideAtLeve（lJ）

3.Jnew←{ }

4. forTask∈TLdo

5. iftis failed then

6.Jnew.add(t)

7. end if

8. ifJnew.size()＞Kthen

9.W=W+Jnew

10.Jnew←{ }

11. end if

12.end for

13.W=W+Jnew

14.returnW

15.end procedure

3.3 平衡重聚類（BR）

本文旨在解決重聚類算法在聚類過程中所面臨的負載不平衡問題。平衡重聚類算在SR 算法的基礎上，根據各層任務運行時間的差異，來調節聚類總運行時間，以達到負載平衡的目的。負載平衡過程類似于HRB 算法，首先根據任務運行時間長短對故障任務列表進行排序。然后進行聚類操作，每次分配運行時間最長的任務至總運行時間最短的聚類。

篩選出運行失敗的任務后，負載平衡的實現仍面臨一個關鍵問題，即聚類規模的確定。聚類個數與總運行時之間存在約束關系。如下所示：

R=min{MLE(T)}

根據需重運行任務的規模、可用資源數量，估計出使得總運行時間最小的聚類個數R。以R作為已知數據輸入，進行平衡重聚類。算法3展示了平衡重聚類算法的偽代碼。

算法3運行時間平衡容錯聚類

輸入：W，科學工作流；R，每一層作業中的聚類數量

輸出：W，科學工作流

1.procedureRECLUSTERING（W，R）

2.TL←DivideAtLevel(W,level)

3.Jnew←{ }

4. fortask∈TLdo

5. iftis failed then

6.Jnew.add(t)

7. end if

8. ifJnew.size＞Rthen

9.C=C+Jnew

10.Jnew←{ }

11.end if

12.end for

13.W=W+Jnew

14.end procedure

15.procedureMERGE(TL,C,R)

16.ifi＜Rthen

17.Jnew←{ }

18.end if

19.CL←{ }

20.sort(TL)

21.fort∈TLdo

22.J.add(t)

23.end for

24.fori＜Rdo

25.CL.add(Ji)

26.end for returnCL

27.end procedure

選擇重聚類將聚類規模簡單定義為運行失敗任務的數量，并不考慮聚類大小對SR 算法的性能影響。但是，實際的最佳聚類規模會隨著故障任務的數量和可用資源數量的變化而改變。動態重聚類算法彌補了選擇重聚類算法的不足，根據可用資源狀況和任務規模計算出最佳聚類規模，每次重新運行時動態地調整聚類規模。與SR 算法和DR 算法相比，BR 算法在解決重聚類算法中負載不平問題的同時，根據資源數量和故障規模計算最佳聚類數，兼并HRB 算法和DR 算法的優點，很大程度地提高了重聚類算法的性能。

4 實驗與分析

4.1 實驗設置

實驗在五個常用科學工作流應用程序上進行，評估了選擇重聚類算法、動態重聚類算法和平衡重聚類算法的性能。五個科學工作流應用程序分別為：天文學應用程序（Montage）、激光干涉引力波天文臺（LIGO）、地震應用程序（CyberShake）、表觀基因組學（Epigenomics）和細菌學應用（SIPHT）。文獻[22]詳細分析和描述了五種工作流各自的結構和特征。

實驗環境由WorkflowSim[23]仿真器提供，Workflow-Sim作為常用的科學工作流實驗仿真環境，提供了20個虛擬機（VM），每一個VM 都有512 MB 的內存，用于模擬真實的分布式環境。平臺提供了五種科學工作流的仿真實現、基礎調度算法、資源分配計劃以及測試程序。測試數據集均由WorkflowGenerator[24]生成，文獻[24]中已經證明WorkflowGenerator 的可用性及其合理性。本實驗在平臺調度階段實現三種重聚類算法，調用測試程序對算法性能進行評估。

實驗首先設置了不同的u（失敗到達間隔時間）值，觀測不同故障率情況下，三種重聚類算法實現后系統總運行時間變化。u的值越高故障產生的概率越小，u的值越低故障產生的概率越大。然后，固定u值，觀測采用BR算法運行前后五種科學工作流負載平衡衡量指標HRV的變化。根據變化情況來評價算法在負載平衡方面的成果。

4.2 實驗結果及分析

實驗中u在任務平均運行時間（平均運行時間由文獻[24]計算得出，如表1所示）的1～10倍范圍內取值，這樣工作流運行時間合理，并且算法的性能差異能夠很好地體現。下面為五個科學工作流中三種重聚類方法的性能對比。

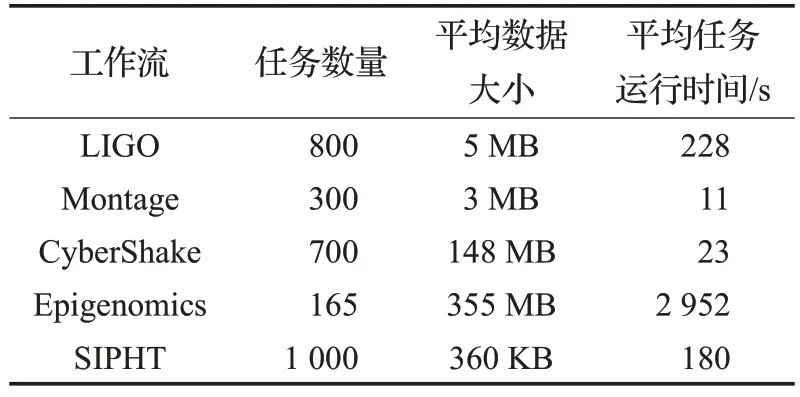
表1 五種科學工作流的特征

Montage：圖4 顯示了Montage 工作流的測試結果，可以看出當故障到達時間間隔u取值較小時，BR算法、DR 算法性能明顯優于SR 算法。隨著u逐漸增大時，BR、DR、SR 算法的性能結果趨于相等。這表明當故障出現的頻率越高，BR算法和DR算法對系統性能提升越大。當u取最小值20 s 的時候，對比BR 算法與SR 算法，性能增益最高為42%。隨著u的增大，性能增益逐漸降低。在u=100 s 時，性能增益為?2.76%。BR 算法相對DR算法的性能增益最高為7.14%，隨著u的增大，性能增益逐漸降至0.61%。

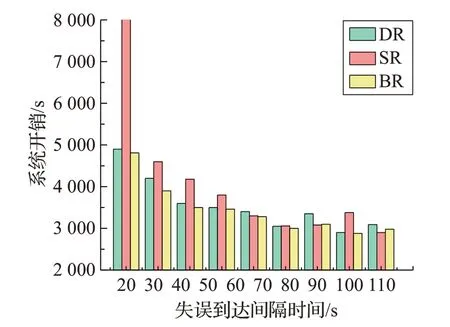
圖4 Montage工作流中三種重聚類算法性能對比

CyberShake：如圖5 所示，三類容錯算法在Cyber-Shake工作流中測試結果的整體變化趨勢與Montage工作流的變化趨勢相似。在u=100 s時，相對SR算法，BR算法的性能增益提高了61.5%，隨后逐漸降低。BR 算法相對DR 算法的性能增益最高為3.79%。當u>500 s時，明顯看到BR、DR、SR之間的性能增益幅度非常小，性能增益均在0.45%以下。

LIGO：LIGO 工作流中三種重聚類算法的實驗結果如圖6所示，BR算法相對SR算法性能增益最高提升了43.0%，最低提高4.2%。當u從800 s增加到2 000 s，BR 相對DR 算法的性能增益逐漸降低，從0.93%降低到?0.19%。這表明BR 算法的性能提升與DR 算法相近。在u=1 000 s處，SR算法性能略高于DR、BR算法。

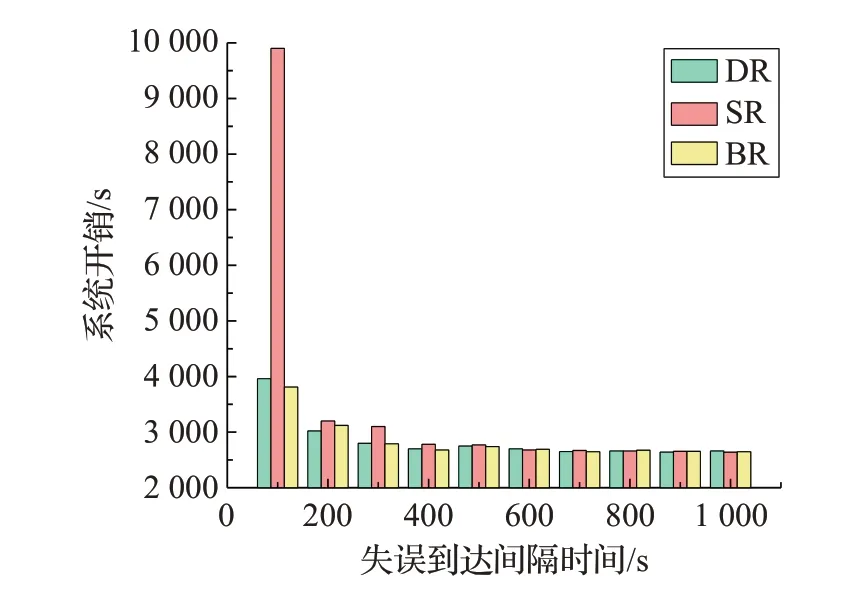
圖5 CyberShake工作流中三種重聚類算法性能對比

SIPHT：圖7 為三種重聚類算法在SIPHT 工作流中的實驗結果。不同于上述三種工作流中，BR相對SR的性能增益隨著u的增加而降低。當u取2 500 s 時，BR算法相對SR的性能增益為61.54%。當u分別取3 500、4 500、5 500時，BR算法相對SR的性能增益分別為9.1%、?0.35%、6.35%。同時，相對DR算法，BR算法的性能增益隨u的增加逐漸降低，從7.89%降到了?0.39%。

Epigenomics：如圖8 所示，為三種重聚類方法在Epigenomics工作流中的實驗結果。與其他四種工作流相比，BR 算法的性能增益明顯高于其他四類工作流。BR 算法相比SR 算法性能增益最高為84.0%，最低為50%。同時，相對于DR 算法，BR 算法性能增益高達18.75%，最低為4.55%，這是一個比較可觀的提升。

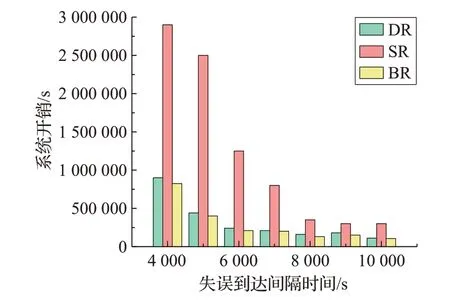
圖8 Epigenomics工作流中三種重聚類算法性能對比

對比三種重聚類算法在五類工作流中的性能表現，可以看出隨著u的變化，性能增益所變現出來的規律有很大差別。為了更好地解釋這一結果，只能根據工作流的機構以及任務運行時間特點進行分析。表1 列舉了五類個科學工作流任務的平均大小和平均任務運行時間，但是缺少了任務運行的細節。因此，設計了第二組實驗，在取定u值的情況下分析BR算法對負載（運行時間）的影響。

根據前面的實驗結果選取平均任務運行時間的一倍作為u值，因為u取該值時，三種重聚類算法性能間的差異更加明顯。取定u值后，分析對比五個科學工作流中執行BR 算法前的HRV 和執行BR 算法后HRV 值的變化，其結果如圖9所示。

Montage：如圖9（a）所示，由于大多從層均為單任務，因此HRV都為0值。而第2、5層HRV值降低非常明顯，下降率分別為85.3%、98.1%。

CyberShake：如圖9（ b）所示，HRV 值在 B R 算法運行前后的下降率最大為55.9%，最小為30.4%。

LIGO：如圖9（c）所示，在第1層中HRV的下降率最高為82.8%，而其他層都低于50%。

SIPHT：如圖9（d）所示，在第3 層HRV 下降率最高為41%，其他層HRV下降率均小于30%。

Epigenomics：如圖9（e）所示，相對其他工作流BR算法運行前后HRV 的下降率，該工作流HRV 下降率較低，最大下降率僅為38.9%。

分析圖9 中五個實驗結果，可以發現較Montage、LIGO中BR算法運行前后HRV的值都非常小，而SIPHT中HRV的值遠高于其他四個的值。結合表1可知，LIGO工作流程的平均任務運行時間相對較短，即使BR 算法運行后平均每層HRV 的值降低了將近50%，而最終的系統開銷相對DR 算法只提升了0.93%，而Montage 中HRV 值的變化最大，在第二層中，HRV 值減小了68%，即使Montage 的平均運行時間相對較小，但BR 算法對于DR算法的性能增益為7.14%。SIPHT工作流的結構非常不對稱，HRV 值相對較高。BR 算法可以通過平衡運行時間進行優化，DR 算法可以通過動態調整聚類大小進行優化，而SR 算法的隨機性較大。這就可以解釋BR 相對SR 算法的性能增益不規律問題。Epigenomics工作流的HRV 值的下降率平均為25%，在level=4 時，HRV值仍為0.64，相對較高。根據表1可知，Epigenomics的平均任務運行時間是Montage 的300 倍，所以將近20%的運行時間平衡導致了系統開銷18.75%的提升。

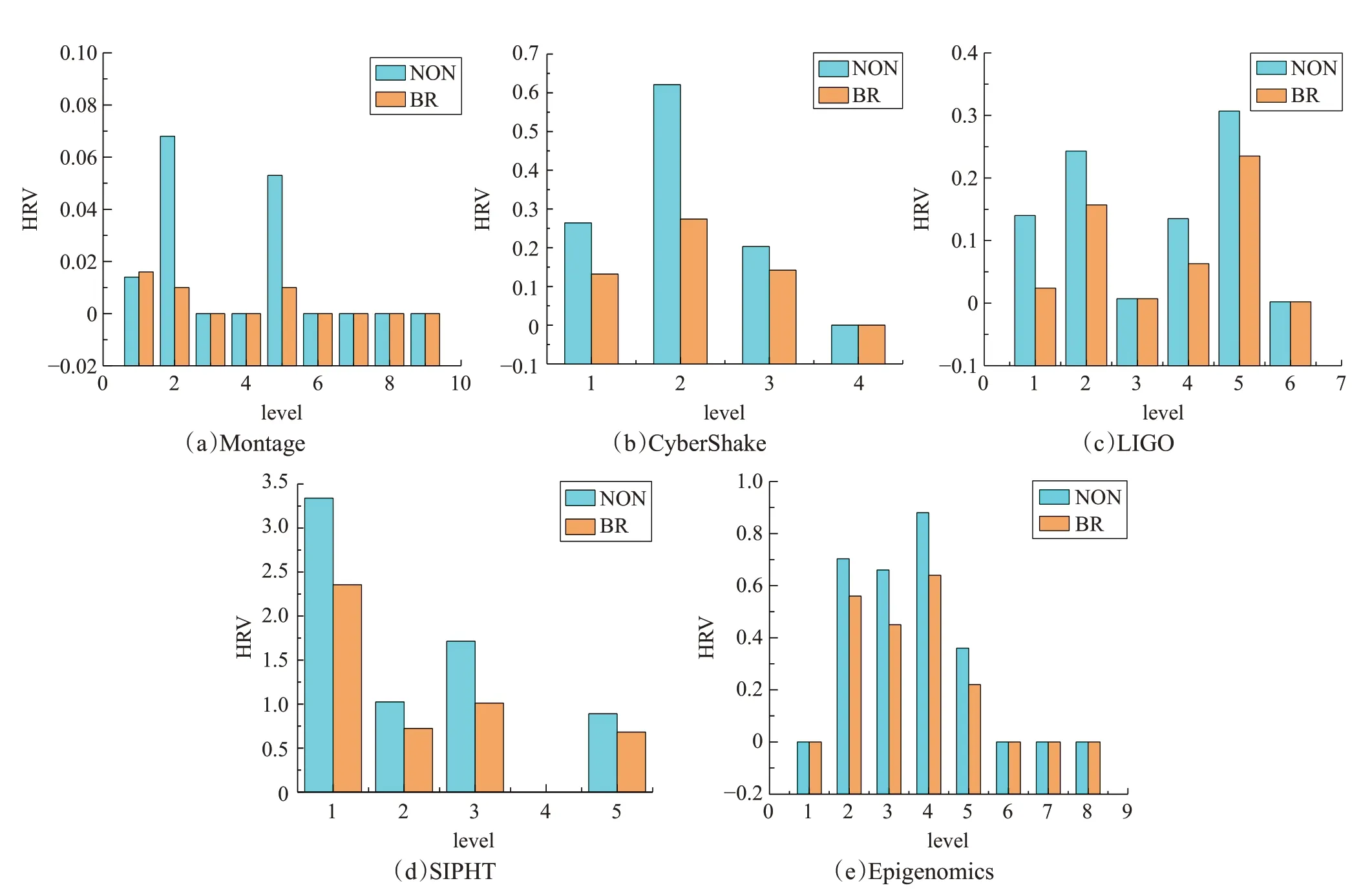
圖9 五種科學工作流中執行BR算法前后HRV的對比結果

結合兩組實驗結果分析，可知當故障出現頻率較高時，平衡重聚類算法性能提升明顯高于動態重聚類算法、選擇重聚類算法。當工作流任務結構不對稱（HRV值較高的SIPHT 工作流）或運行時間嚴重不平衡時（例如，Epigenomics 工作流），即使故障率較低下，BR 算法對工作流系統的運行效率仍有較大的提高。

5 總結

為解決容錯聚類算法面臨的負載不平衡問題，本文提出了一種考慮任務運行時間平衡的容錯聚類算法BR，通過調整模型中故障出現頻率測試算法性能。實驗結果表明，在故障率較高的情況下，與現有的任務容錯聚類方法相比，BR 算法顯著降低了科學工作流的完工時間，在故障率較低的情況下，平衡容錯聚類方法在Epigenomics 工作流中表現最佳。BR 算法采用水平運行時間平衡方法來解決負載平衡問題，未來的工作可以考慮任務間距離平衡或依賴關系平衡方法與容錯聚類方法的結合。根據不同工作流呈現出的不平衡問題，推薦相應的平衡重聚類算法。