數列綜合應用“三劍客”

◇ 山東 李愛霞 梁桂媛

數列是高中數學的重要內容之一,也是歷年高考考查的重點之一.特別是數列綜合應用問題,往往還以解答題的形式出現,所以我們在復習時應給予重視.近幾年高考數列的綜合應用試題從數列的概念、等差數列和等比數列的基礎知識、基本技能和基本思想方法入手,涉及函數、方程、不等式、解析幾何、概率等知識的綜合性試題,在解題過程中通常用到等價轉化、分類討論等數學思想方法,是屬于中高檔難度的題目.下面結合數列綜合應用常見的“三劍客”加以實例剖析.

1 探究性問題

例1已知數列{a n}滿足a1＝1,a n·a n＋1＝a n－3a n＋1.若.

(1)求數列{c n}的前n項和S n;

(2)試問:是否存在互不相同的正整數p,q,r,使S p,S q,S r成等差數列?若存在,求出p,q,r的最小值;若不存在,請說明理由.

解析

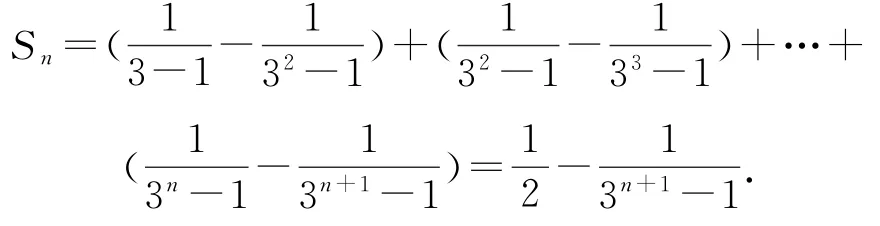
(2)若存在互不相同的正整數p,q,r,使S p,S q,S r成等差數列,不妨設p＜q＜r,則

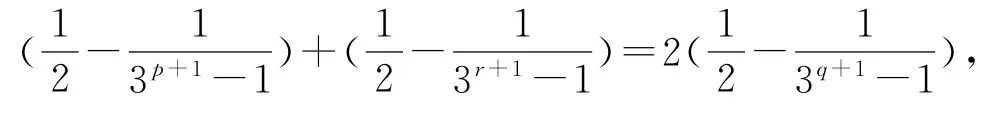
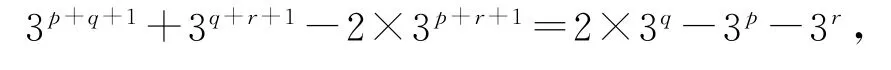
等號兩邊同時除以3q,得

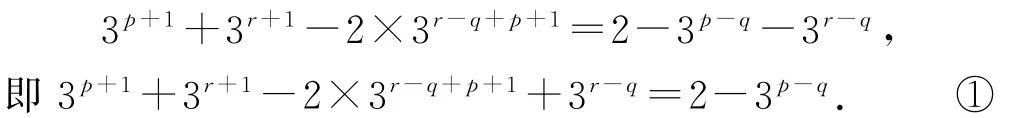
因為p,q,r∈N?,且p＜q＜r,所以r－q∈N?,r－q＋p＋1∈N?,故式①等號左邊3p＋1＋3r＋1－2×3r－q＋p＋1＋3r－q為整數,而p－q＜0,所以3p－q∈(0,1),所以式①等號右邊2－3p－r∈(1,2),所以不存在互不相同的正整數p,q,r,使Sp,Sq,Sr成等差數列.

點評

20世紀80年代以來，越來越多的攝影藝術家開始采用“設計”的方式進行創作。他們有意識地跟隨廣告業照亮的道路，運用想象與才智掙脫了古典現代主義的束縛。他們不是在現實世界中尋找主題，直接“拍攝”，而是選擇自行“創造”一個全新的視覺世界。

數列中的探究性問題,往往以開放性與探索性等形式出現,此類問題以等差數列、等比數列等基本知識為基礎,綜合數列的定義、通項公式、求和公式,用來判斷數列的類型、存在性問題,利用開放思維創新、探索思維拓展等加以考查與應用.

2 恒成立問題

例2已知λ＜0,數列{an}滿足an＋1－λan＝λ－λ2(n∈N?),且a1＝3λ.

(1)求證:數列{an－λ}是等比數列;

(2)若對任意的m,n∈N?,都有恒成立,求實數λ的取值范圍.

解析

(1)因為an＋1－λan＝λ－λ2,所以an＋1－λ＝λ(an－λ),因為a1＝3λ,λ＜0,所以a1－λ＝2λ＜0,從而an－λ≠0,所以,所以數列{an－λ}是首項為2λ、公比為λ的等比數列.

(2)由(1)知an－λ＝2λ·λn－1,即an＝2λn＋λ,據題意知得－1＜λ＜0.當n＝2k,k∈N?時,a2k＝2λ2k＋λ＞λ,故

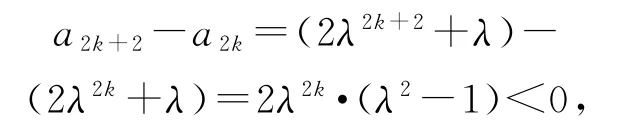
當n＝2k－1,k∈N?時,a2k－1＝2λ2k－1＋λ＜λ,故

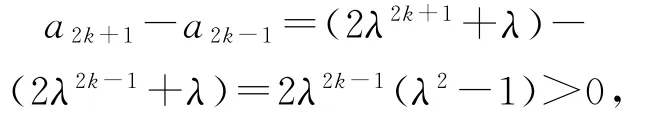
所以數列{a2k－1}單調遞增;

因為對任意m,n∈N?,都有,所以

且0＞a2＞a4＞a6＞…＞a2k＞…＞λ,所以的最小值為所以.

綜上所述,實數λ的取值范圍是.

點評

數列恒成立問題能夠很好地考查數列、函數、不等式等知識以及化歸與轉化等數學思想,因此備受命題者青睞,在復習時要有針對性地訓練,從而靈活掌握與應用.加強這一類問題的訓練有利于提高綜合解題能力,在培養思維的靈活性、創造性等方面起到積極的作用.

3 創新定義問題

例3若無窮數列{an}滿足:存在k∈N?,對于任意的n≥n0(n0∈N?),都有an＋k－an＝d(其中d為常數),則稱{an}具有性質“P(k,n0,d)”.

(1)若{an}具有性質“P(3,2,0)”,且a2＝3,a4＝5,a6＋a7＋a8＝18,求a3;

(2)若無窮數列{bn}是等差數列,無窮數列{cn}是公比為正數的等比數列,b1＝c3＝2,b3＝c1＝8,an＝bn＋cn,判斷{an}是否具有性質“P(2,1,0)”,并說明理由.

解析

(1)因為{an}具有性質“P(3,2,0)”,所以an＋3－an＝0,n≥2,由a2＝3,得a5＝a8＝3,由a4＝5,得a7＝5,因為a6＋a7＋a8＝18,所以a6＝10,即a3＝10.

(2){an}不具有性質“P(2,1,0)”.

設等差數列{bn}的公差為d,由b1＝2,b3＝8,得2d＝8－2＝6,所以d＝3,故bn＝3n－1.設等比數列{cn}的公比為q,由c3＝2,c1＝8,得又q＞0,所以所以an＝3n－1＋24－n,若{an}具有性質“P(2,1,0)”,則an＋2－an＝0,n≥1.

因為a2＝9,a4＝12,所以a2≠a4,故{an}不具有性質“P(2,1,0)”.

點評

數列創新定義的綜合問題往往是在等差數列、等比數列的基礎上加以類比、提升與拓展,解決此類問題往往需要將其轉化為熟悉的等差數列、等比數列來分析與求解,實現創新能力與轉化思維的統一,知識與能力的綜合,達到創新目的.

由于數列是特殊的函數,而不等式是深刻認識與解析函數和數列的重要工具之一,三者的交會并以探究性、恒成立或創新定義等形式出現,是近年來高考命題的新熱點.