基于數據清洗與組合學習的光伏發電功率預測方法研究

邱 明， 魯冠軍， 吳昊天， 楊仲卿

（1. 重慶大學 能源與動力工程學院， 重慶 400044； 2. 重慶電力高等專科學校 動力工程學院， 重慶400053； 3.華北電力大學 電氣與電子工程學院， 北京 102206）

0 引言

由于光伏發電系統具有可持續、 環境友好和發電效率較高等特點，因此，該系統越來越受到人們的重視。目前，我國光伏行業已進入了產業結構調整階段， 各光伏企業均由原來的粗獷式發展模式轉變為精細化發展模式。 2019 年，我國光伏市場結構調整初見成效， 分布式光伏電站和集中式光伏電站的占比逐漸趨于平穩， 光伏市場的發展狀況也趨于穩定。 在如此大規模的光伏發電接入電力系統的情況下， 如何有效協調可再生能源和常規能源的規劃與運行， 是當前可再生能源持續發展的關鍵問題。 可再生能源出力的不確定性給整個能源系統帶來極大挑戰。 因此， 須要對集中式、 分布式太陽能光伏發電系統的出力情況均進行 有 效 預 測[1]，[2]。

從上世紀70 年代開始，針對光伏發電功率預測問題，國內外學者已經展開廣泛研究。光伏發電功率預測方法通常包括直接計算法和間接計算法。其中，直接計算法可基于氣象參數變化過程計算得到光伏發電輸出功率； 對于基于數據驅動的間接法， 使用機器學習模型對歷史輸出數據進行訓練學習。間接計算法包括序列建模算法、支持向量 回 歸（Support Vector Regressor，SVR）、神 經 網絡（Artificial Neural Network，ANN）和混合建模方式[3]～[8]。文獻[9]分析了目前常用的光伏發電功率預測方法，包括點預測和概率預測，并分別對當前的預測算法和評價指標等進行了梳理、歸類和總結。文獻[10]提出了一種分布式光伏電站預測模型，該模型使用臨近區域的光伏電站進行建模， 使用長短期記憶網絡對時間特征進行抓取， 使用圖卷積網絡對電站空間特征進行提取， 并根據提取的時空特征信息和歷史數據來訓練光伏發電預測模型。 文獻[11]采用深度學習方法對光伏出力進行預測，預測結果表明，深度學習算法優于淺層學習算法。 文獻[12] 提出了一種小波變換（Wavelet Transform）與神經網絡相結合的預測算法，并利用該算法對光伏陣列的超短期功率進行了有效預測。 文獻[13]在泛在電力物聯網背景下，提出了一種基于Elman 網絡的光伏出力預測模型，并采用智能算法對該預測模型的權值進行優化， 以提高預測精度。 文獻[14]針對環境溫度、環境濕度和太陽輻照度3 個因素， 建立基于云團變化的光伏短期發電功率預測模型和普適性的云規則生成器，利用主成分分析法對輸入數據進行降維處理，并使用遺傳算法對預測模型進行優化， 分析結果表明，該模型具有良好的預測能力。 文獻[15]重點分析了光伏電站數據的質量， 并采用清洗方式對數據進行異常處理，此外，根據預測模型的成本約束和運行需求， 提出一種基于核函數極限學習機的分布式光伏發電功率預測方法。

在復雜的光伏電站運行環境下， 本文提出了一種基于數據清洗與組合學習的光伏發電功率預測方法。考慮到變電站實際運行時，通信與傳輸過程中的數據遺漏狀況， 在數據輸入模型前采用KNN 算法對缺失數據進行補全；然后，利用Lasso算法將極限學習機 （Extreme Learning Machine，ELM）、 神經網絡模型和Adaboost 模型的預測結果進行動態組合，以獲得最終預測結果；最后，采用北京大興區的實際光伏發電數據來驗證模擬結果的準確性。

1 預測模型及算法機理分析

1.1 基于KNN 算法的數據清洗方式

本文研究對象為光伏電站。 光伏電站一般處于配電網和電壓等級較低的輸電網中， 屬于電力系統的末端環節， 該電壓等級下的電網并不能如大電網一樣做到精細化管理。 配電網和電壓等級較低的輸電網的通信和信息系統發展得相對滯后， 使得該電壓等級下電力系統中測量誤差和傳輸設備故障率均較高， 使得設備可靠性變差。 此外， 配電網中管理調度人員的數量和維修人員的專業素質也有待提高， 人為因素造成的數據質量不高的狀況也應該得到高度重視。

光伏電站數據極易出現缺失， 如果不對缺失數據進行有效清洗， 直接將缺失數據嵌套入預測模型進行訓練，對預測模型產生巨大影響，從而導致光伏出力預測的精度大幅度降低。 對于降壓變電站的數據缺失問題，預測模型使用KNN 算法進行數據清洗，KNN 算法是缺失數據清洗中較為有效、計算復雜度較低的算法，在機器學習實際工程的數據預處理方面得到廣泛應用，考慮到KNN 算法中歐式距離越近，數據間相似度越高這一情況，KNN 算法選取了數據集中與缺失數據最近鄰的、最完整的k 個數據補全缺失值。KNN 算法模型的計算式為

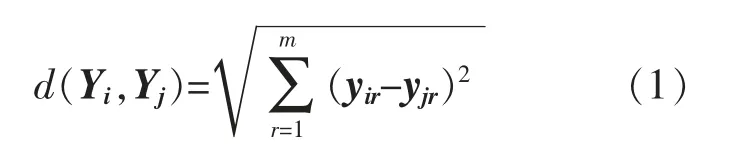
式中：Yi為第i 個樣本點的前m 維特征向量，Yj=（yi1，yi2，yi3，…，yir），其中，yir為第i 個樣本點的第r維屬性。

1.2 核函數極限學習機

ELM 屬于單層前饋神經網絡算法。ELM 輸出函數f（x）的表達式為

式中：h（x）為隱藏層計算所得的輸出；β為隱藏層與輸出層之間的連接權重，β=[β1，…，βL]T。

核函數極限學習機的誤差表達式為

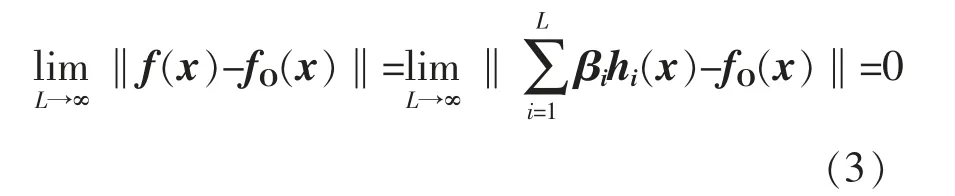
式中：L 為神經元的數目；βi，hi（x）分別為第i 個節點的權值和輸出值；fO（x）為真實標記值。

核函數極限學習機的基本架構如圖1 所示。

圖1 核函數極限學習機的基本構架Fig.1 Kernel-based extreme learning machine

核函數極限學習機輸出函數fL（x）的表達式為

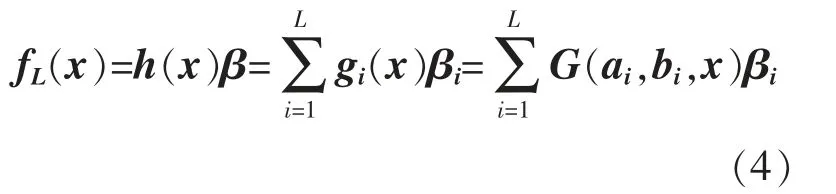
式中：gi（x），G（ai，bi，x）均為第i 個隱藏節點的輸出函數；ai，bi均為隱藏層參數。

訓練前饋神經網絡所需要權重的最優二乘解的表達式為

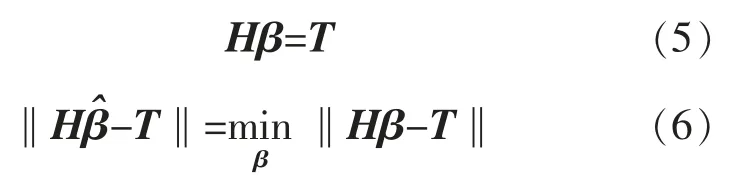
式中：T 為預測目標值；H 為神經網絡隱藏層矩陣。

模型輸出權重的最小標準二乘解表達式為

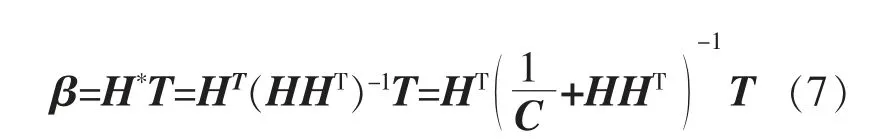
式中：H*為H 的廣義逆矩陣；1/C 為常數。

式（7）中的1/C，能夠使求解結果具有更好的泛化能力。

1.3 Adaboost 模型

Adaboost 模型為疊加集成模型， 它訓練了多個弱擬合模型，然后將各個弱擬合模型組合起來，構成一個強預測模型。 其總體思路是對正確樣本賦予較低權值，對錯誤樣本賦予較高權值，通過不斷加權組合，提高預測模型的性能。

Adaboost 模型的計算步驟如下。

①從樣本中選取n 組訓練數據， 設初始化數據的分布權值為Di（i）=1/n。

②在訓練第t 個弱學習器時， 用訓練數據訓練決策樹，從而得到誤差之和et為Dl（i）。

③根據預測誤差之和et計算弱學習模型的權重αt。 αt的計算式為

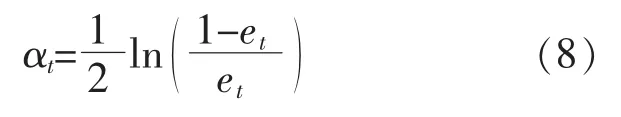
④根據弱學習器調整下一輪訓練樣本的權重，更新公式為

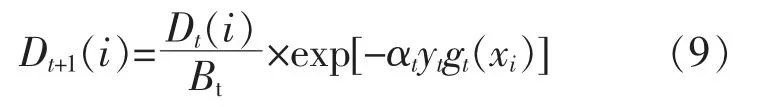
式中：Dt（i）為第t 輪的權值，i=1，2，…，n；yt為第t輪的學習器；Bt為第t 輪的歸一化因子。

⑤訓練T 輪以后， 得到T 組弱學習器f（gt，αtt）， 由T 組弱學習器組合可以得到一個強學習器h（x）。 h（x）的計算式為

1.4 Lasso 回歸方法

Lasso 回歸方法是基于正則化的線性回歸分析方法， 主旨思想是在相關系數絕對值之和小于一個閾值的條件下，使得殘差的平方和最小化。

普通線性模型的表達式為

式中：Y 為最終負荷的預測值；X為第一層模型的預測值，X=（X（1），X（2），X（3）），其中，X（1），X（2），X（3）分別為第一層模型中ELM 模型、Adaboost 模型和ANN 模 型 的 預 測 值；ε 為 隨 機 誤 差 項，ε=(ε1，ε2，..，εn)；r 為回歸系數。

Lasso 回歸方法估計的表達式為

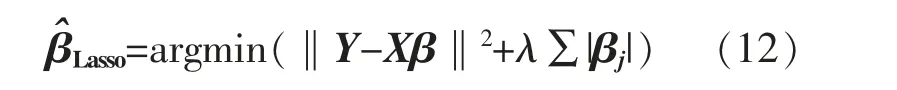
在模型訓練過程中須要求解權重， 當權值計算完成后，表明負荷預測模型已建立完成。

2 基于數據清洗與組合學習的光伏發電功率預測模型

本文預測模型的建立過程包括數據清洗、模型訓練和預測指標等過程。在數據的預處理階段，數據清洗是整個數據分析過程中不可缺少的一環，也是較易被忽視的一環，以往的文獻并沒有對其足夠重視， 數據清洗的質量直接決定了模型預測效果。在實際工程應用中，數據清洗時間往往占分析過程的50%～80%。由各電壓等級光伏電站的實際情況可知， 低電壓等級光伏電站的管理水平較低，相對來說，數據缺失的概率較高。因此，須要在數據輸入模型前充分對數據進行清洗。 本文選取了光伏輸入相關特征，輸入數據包括總輻射S、組件溫度Td、環境溫度To、氣壓A、相對濕度H 和歷史光伏發電功率P 進行數據清洗[12]。

單個模型容易陷入局部最小值， 且統計假設空間有限， 本文采用的模型組合可以提高預測算法的可靠性。 對于ELM 模型、Adaboost 模型和ANN 模型的預測結果， 采用Lasso 線性組合的方式進行學習。 為了確保Lasso 算法中各參數的實時性， 本文采用動態更新的方式改變Lasso 算法中的各個參數， 從而獲得時序滾動的光伏預測模型，保證當前模型與數據的相互匹配。圖2 為時序滾動的光伏功率預測模式。

圖2 時序滾動的光伏功率預測模式Fig.2 PV output forecasting time horizon-rolling

本文模型的訓練流程：首先，采用KNN 算法對缺失數據進行填充， 將填充后數據輸入到ANN模型、Adaboost 模型和ELM 模型中，并分別對這3個模型進行訓練； 為了避免ANN 模型和ELM 模型計算結果不確定性的影響， 本文以多組不同的參數值對ANN 模型和ELM 模型進行初始化，并從多個不同的初始點開始探索， 從而有效避免陷入不同的局部極小值， 然后獲得更接近全局最小的結果；最后，將各模型的預測結果輸入Lasso 線性模型，得到最終的光伏功率預測結果。基于數據清洗與模型組合的光伏功率預測方法的計算流程圖如3 所示。

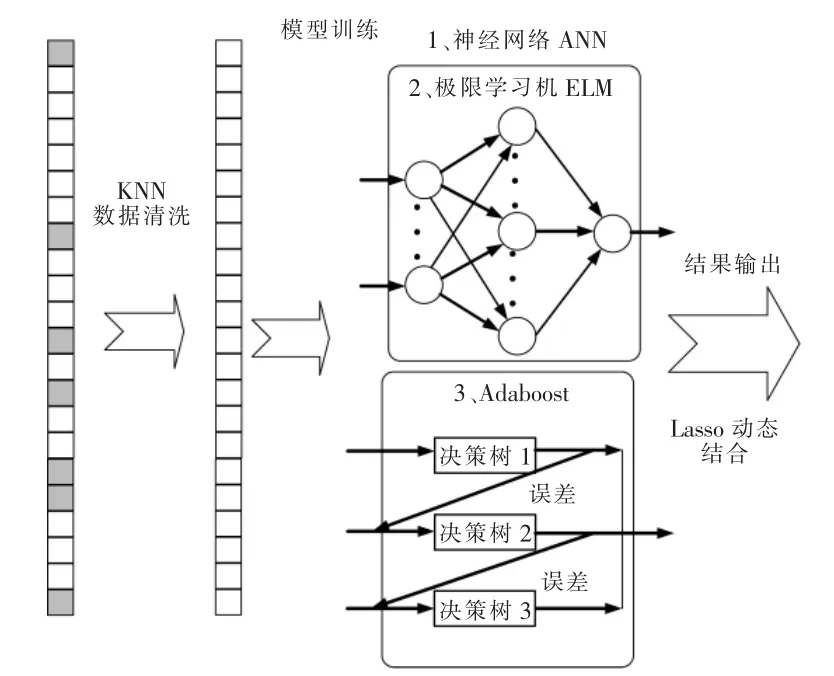
圖3 基于數據清洗與模型組合的光伏功率預測方法流程圖Fig.3 PV output forecasting based on data cleansing and model aggregation

3 算例分析

本文選用北京大興區的光伏發電系統實際運行數據對模擬結果進行驗證。 光伏發電系統總裝機容量分別為400 kW，4 MW， 選取2017 年數據為訓練數據，2018 年1 月份數據為測試數據。

本文的誤差指標主要包括均方根誤差（Root Mean Square Error，RMSE） 和標準化平均相對誤差（Normalized Mean Absolute Error，nMAE）。

RMSE，nMAE 的表達式分別為

式中：fi，ti分別為i 時刻光伏發電系統的實際發電功率和預測發電功率；tm為最大裝機容量。

3.1 數據預處理方案對比

為了分析不同數據填充方案的優劣，將KNN補全算法、 線性插值的補全方法和不使用補全算法的計算結果進行對比。在相同的模型架構下，分別采用3 種方式對模型進行訓練。

不同數據補全算法對預測結果影響見表1。

表1 不同數據清洗算法對預測結果的影響Table 1 Effect of different data cleansing algorithm

由表1 可知，電壓等級越低、額定容量越小的光伏電站，數據缺失的情況越嚴重，這表明光伏電站的管理水平與電壓等級具有相關性， 即電壓等級越低、 額定容量越小的光伏電站的管理水平越低。 不同類型的光伏電站預測功率呈現不同的誤差分布。此外，不使用補全算法對預測精度影響很大， 這是由于刪除缺失數據的信息破壞了數據原有的內部特征，使得預測精度大幅度降低。采用線性插值方法時， 只能考慮輸入數據中單一特征變量的存量數據結構， 對于缺失數據也只是簡單的采用線性方法進行補全，因此，線性插值方法預測精度的提升幅度有限。利用KNN 補全算法對缺失數據進行填充，能夠較好地還原數據初始形態，使得預測結果的精度較高。

3.2 預測效果對比分析

Lasso 算法動態地學習了各個模型的權重。因此，須要分析各個子模型對應權值的趨勢。圖4 為Lasso 模型權值隨時間的變化情況，圖中：β1，β2，β3分別為ELM 模型，Adaboost 模型和ANN 模型的權值。

圖4 Lasso 模型權值隨時間變化情況Fig.4 Time-varying weights of Lasso model

由圖4 可知，Lasso 模型在不同時段通過計算獲得不同模型的權值， 說明在當前預測場景條件下， 各模型具有不同的優勢，Lasso 算法能夠充分學習到各個子模型的優點， 使得預測效果得到進一步提升。

天氣情況對光伏輸出功率影響較大。因此，為了進一步驗證本文算法的準確性和優越性， 分別在晴天和陰天的場景下， 對組合學習模型和單模型（ANN）的預測結果進行分析。 圖5 為不同天氣條件下， 額定輸出功率分別為400 kW，4 MW 的光伏發電系統輸出功率的預測結果隨時間的變化情況。

圖5 不同天氣條件下，不同額定輸出功率光伏發電系統輸出功率的預測結果隨時間的變化情況Fig.5 PV power output forecasting under different weather conditions as time change with different rated power

將本文組合學習預測模型的預測結果與SVM 模型[6]、ANN 模型[7]和時間序列算法[8]的預測結果進行比較。 其中，ANN 模型的內置節點分別為14，100，1；SVM 模型核函數參數為徑向基函數，懲罰系數為1 000，核函數系數為10-3。各個算法的預測結果如表2 所示。

表2 不同場景下多個模型的光伏預測誤差Table 2 Photovoltaic forecasting error of several models

由表2 和圖5 可知，與陰雨天氣相比，晴朗天氣下各個模型的預測精度較高， 這是因為晴朗天氣下光伏出力的變化較為平穩， 導致光伏出力的變化曲線較為平滑。此外，在陰雨天氣下各個模型的預測誤差普遍偏大， 這是由于云層與太陽輻照度的變化使得光伏出力產生突變。 對于模型的預測效果而言，相較于其他模型，組合學習模型的計算結果能更好地顯示出光伏出力的變化趨勢。 在多個光伏預測的場景下， 本文模型均獲得了最高的精度和泛化能力， 這是因為本文組合模型聚合了多種學習算法， 并將其動態結合以提高本文模型的泛化性和魯棒性。對其他算法而言，神經網絡只使用了單一學習方法，容易陷入局部極小值，使得整體泛化性不高。 支持向量機輸入數據挖掘的信息有限，雖然該算法也有較高的預測精度，但仍低于本文的預測方法。 時間序列算法的學習能力較弱， 只能計及光伏的歷史信息， 預測精度也偏低。由此可見，本文使用的組合預測模型對于電力系統制定合理的運行策略有著較高參考價值。

4 結論

本文提出一種基于數據清洗與組合學習的光伏發電功率預測方法。 考慮到變電站實際運行中通信和傳輸過程中的數據遺漏情況， 在數據輸入模型前采用KNN 算法對缺失數據和異常數據進行清洗，然后，通過Lasso 算法將ELM 模型、ANN模型和Adaboost 模型的預測結果進行動態組合。模擬結果表明：利用KNN 算法能夠良好地清洗光伏發電站中的缺失數據和異常數據， 使得整體數據能夠恢復到原有特征； 組合學習方式能夠充分發揮多種算法的優勢， 針對不同容量的光伏電站均有良好的預測結果； 晴天條件下， 本文模型的RMSE相較于神經網絡、 支持向量機和時間序列分別提高了1.22%，1.83%，2.99%，陰雨天條件下，本文模型的RMSE 分別提高了0.66%，1.78%，4.68%。

目前，本文模型主要圍繞點預測展開，概率預測與組合學習方式的結合仍然有待于深入挖掘，數據的填充方式只考慮了同一尺度數據的相互關系，對于歷史數據的變化趨勢仍值得深入分析。