某中低速磁浮軌道巡檢車動力學特性研究
朱震寰
(中國鐵建重工集團股份有限公司 湖南長沙 410100)
1 前言
中低速磁浮由于其環境友好、選線靈活的優勢在各種類型新型軌道交通中具有很強的優勢,并持續獲得越來越廣泛的應用[1-2]。在中低速磁浮系統中,列車與軌道的匹配精度要求高,保證良好的軌道狀態是保證行車舒適和安全的基礎。在運營過程中軌道檢測是保證安全運行的主要措施。
目前,在磁浮軌道巡檢研究領域,鄧贊[3]對磁浮維護牽引車車輛系統進行了動力學仿真。曾長操等[4]研究了高速磁浮軌道巡檢車的側向動力學性能和導向系統的安全性。張耿等[5]73建立了唐山低速磁浮試驗線的軌道不平順譜。德米特里·波戈列洛夫等[6]基于Universal Mechanism(UM)開發了磁浮列車-軌道梁耦合振動仿真的專用程序UM Maglev。陳琛等[7]采用虛擬激勵法將軌道不平順產生的隨機激勵轉化為系統輸入激勵。Zhang等[8]研究了基于機器視覺檢測技術的中低速磁浮F軌軌縫的動態檢測方法。魏高恒等[9]分析了不同波長的軌道垂向激勵對磁浮車輛系統動力學的影響。
CXJ-5磁浮智能巡檢車是中國鐵建重工集團股份有限公司針對中低速磁浮軌道線路智能巡檢功能而開發的一種集人員輸送及軌道檢測于一體,具備高速巡檢和低速精細檢測模式的新型中低速磁浮軌道工程作業車。該車設計的高速走行速度為25 km/h、低速檢測速度為5 km/h。為了提升磁浮智能巡檢車運行速度,并保證其平穩性,增強其適用性,本論文通過建立動力學模型仿真以及工程試驗驗證來研究該車的動力學特性,并進行優化設計。
2 中低速磁浮軌道巡檢車動力學模型
中國鐵建重工集團股份有限公司研制的磁浮智能巡檢車如圖1所示。
該車主要由車體、底盤、檢測小車及附件構成。根據巡檢車的結構,巡檢車的基本組成為:車體、車架、車橋、車輪,其中車體通過6個減振器與車架相連、車架通過4個橡膠減振組件與2個車橋相連、車輪與車軸可相對轉動。車輪與軌道的相互作用力采用Pacejka輪胎模型表示,并將徑向剛度提高,以模擬實心橡膠車輪與軌道的作用力。車架四周的4個導向裝置采用車架與軌道間的彈簧模型模擬,整車模型拓撲圖如圖2所示。

圖1 中低速磁浮智能巡檢車
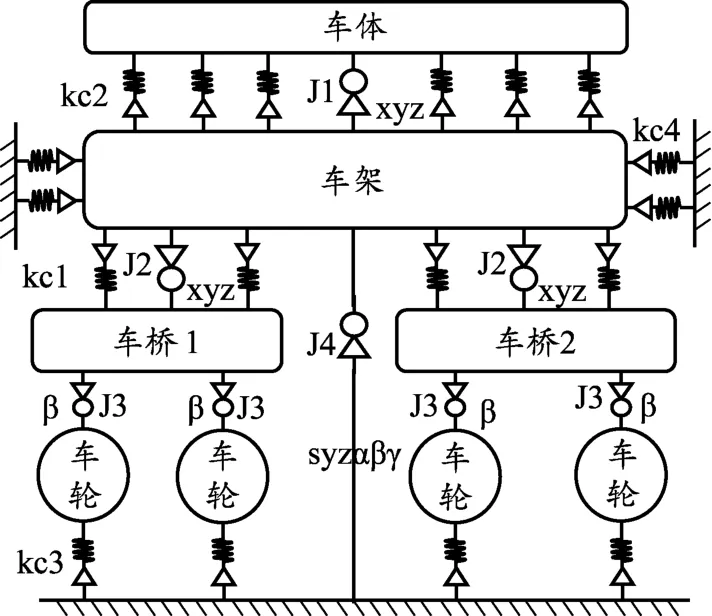
圖2 中低速磁浮軌道巡檢車動力學拓撲模型
圖2中車體與車架采用xyz三自由度鉸連接,車架與車橋采用xyz三自由度鉸連接,車橋與車輪之間采用β轉動自由度鉸連接,車架與地面間采用syzφγψ六自由度鉸連接,車架與車橋間橡膠襯套采用動剛度彈簧單元模擬,車體與車架間的減振器采用彈簧阻尼單元模擬,車輪與地面接觸模型采用Pacejka輪胎力模型模擬,導向機構與軌道的導向力采用彈簧單元模擬。
2.1 主要計算參數(見表1)
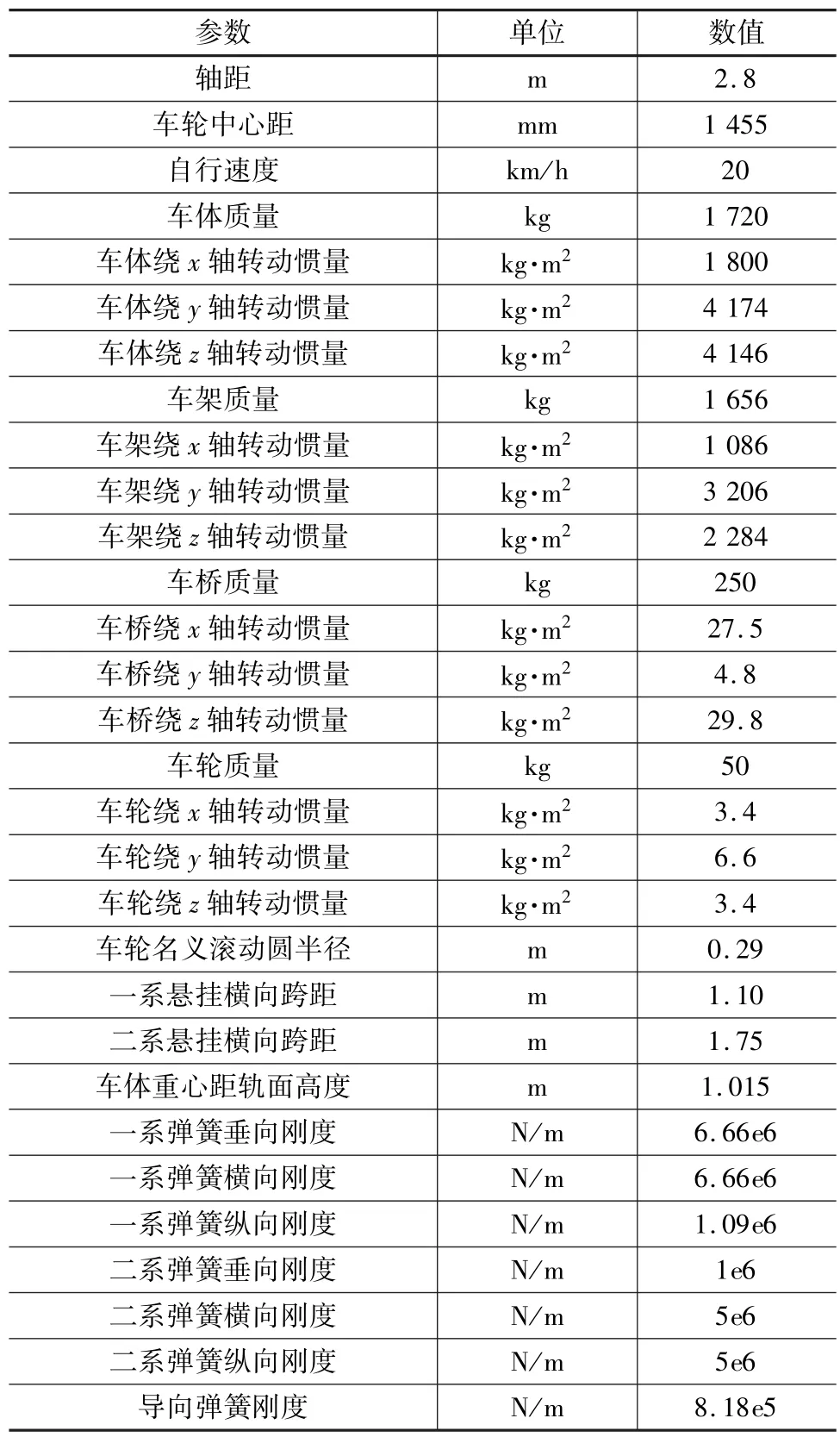
表1 模型參數
2.2 輪胎模型
魔術公式是用三角函數的組合公式擬合輪胎試驗數據,用一套形式相同的公式表達輪胎的縱向力Fx、側向力Fy、回正力矩Mz、翻轉力矩Mx、阻力矩My以及縱向力、側向力的聯合作用工況。
魔術公式的一般表達式為:

式中,Y(x)可以是側向力、回正力矩或者縱向力,自變量x可以在不同的情況下分別表示輪胎的側偏角或縱向滑移率,式中的系數B、C、D依次由輪胎的垂直載荷和外傾角來確定。
本文基于車輪靜載試驗數據以及文獻[10-12],選擇較大的徑向剛度數值和較小的軸向剛度數值,設定車輪參數如表2所示。

表2 車輪參數 N/m
2.3 軌道激勵
中低速磁浮軌道主要由F軌、軌枕、減振元件、接頭等構成,由于結構與鐵路不同,現有的軌道譜不適合作為磁浮軌道上走行的車輛仿真使用。本文基于張耿等[5]76的研究,設定軌道譜如圖3所示,波長范圍設為0.3~16 m。
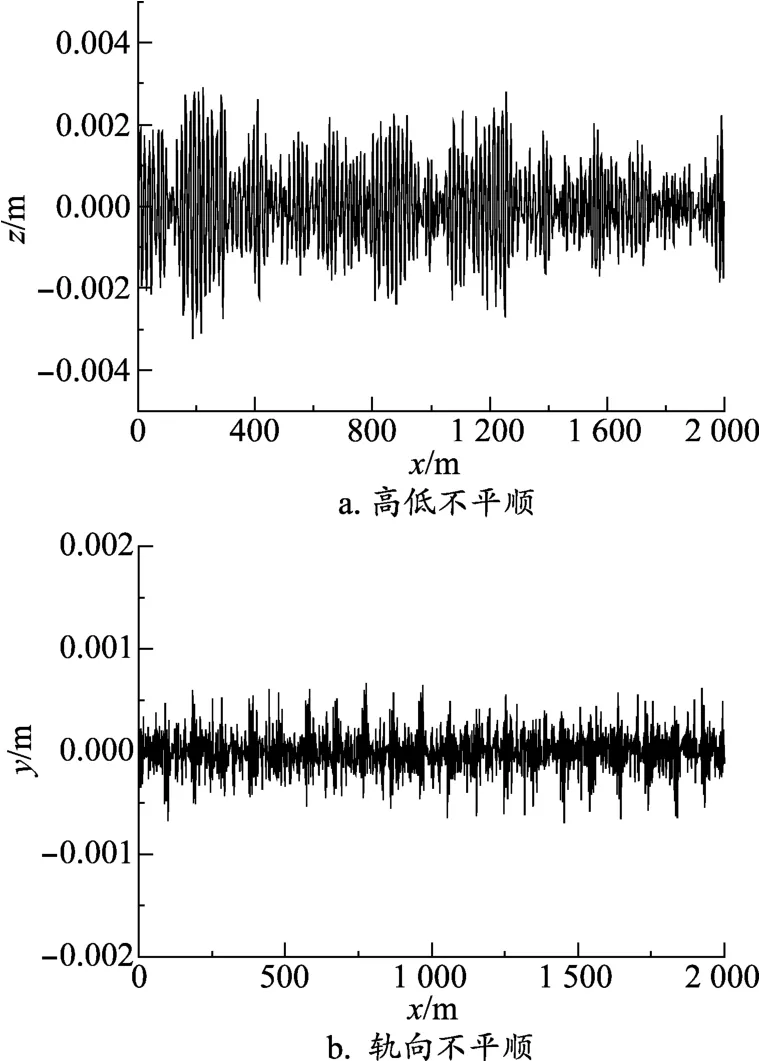
圖3 軌道不平順譜(時域)
3 工程試驗概述
在某磁浮試驗線上進行工程試驗,試驗速度20 km/h,直線段距離為2.2 km的線路進行勻速走行。在座椅安裝座處布置加速度傳感器(美國LORD無線加速度傳感器G-LINK-200)。設定采樣頻率為256 Hz。將加速度傳感器安裝使得Z軸設為豎直方向、X軸設為車輛前進方向,Y軸設為車輛的橫向。
4 結果及討論
4.1 垂向加速度
如圖4所示,圖4a為動力學仿真所得的車體座椅處垂向加速度的仿真值,圖4b為加速度的頻譜分析圖。
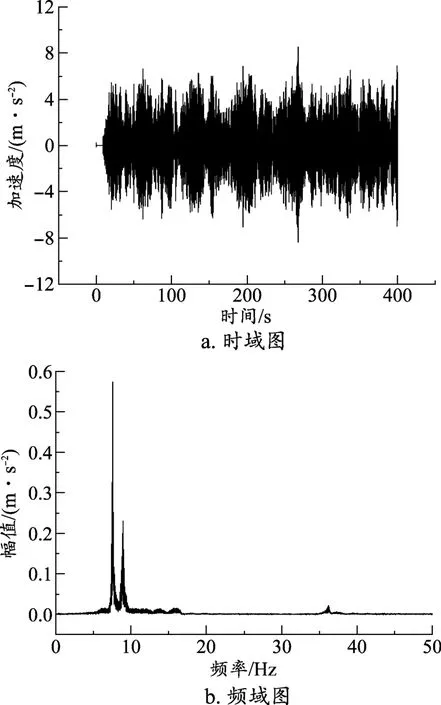
圖4 車體垂向加速度仿真值
如圖5所示,圖5a為在線路上試驗所測量得到的車體座椅處垂向加速度的實測值,圖5b為加速度的頻譜分析圖。
對比圖4與圖5,車體的垂向加速度仿真所得最小為-8 m/s2、最大為8 m/s2,實測所得最大值為8 m/s2,最小值為-14 m/s2。在頻譜圖中仿真模型的垂向振動能量集中在9 Hz、36 Hz等頻率上,實測的垂向振動能量集中在3 Hz、9 Hz、35 Hz等頻率上。這表明本文所建立的磁浮智能巡檢車的動力學模型可以基本反映垂向振動幅度。不足之處在于振動能量頻率來源不夠完全,這是因為軌道不平順所含的頻率種類不夠,比如實際的磁懸浮軌道的隨機不平順功率譜具有分段特征[13],本論文采用的不平順譜不完全反映實際磁浮軌道不平順特征[5]76。具體分析梁自身的頻率成分[14-15]包括一階豎向頻率5.365 Hz、二階豎向頻率8.950 Hz、三階豎向頻率9.859 Hz,其中的二階、三階頻率也是車體振動的主頻率,因此論文所建模型可以反映車輛運行過程中的車體振動特性。
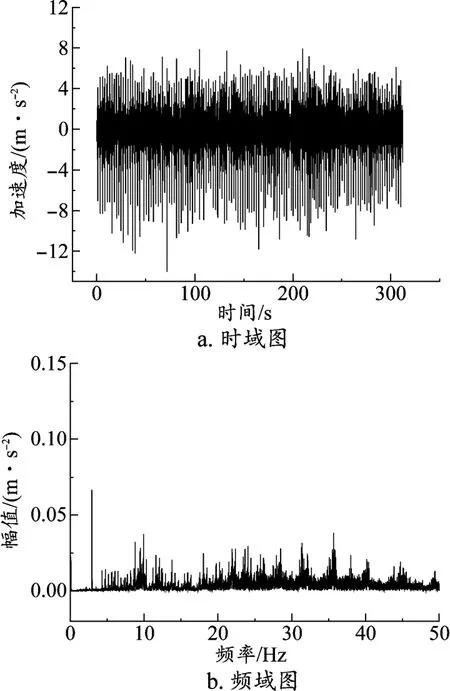
圖5 車體垂向加速度實測值
分析垂向振動的頻譜發現,車輛在8~10 Hz的區域內,振動能量大。而二系的固有頻率為:
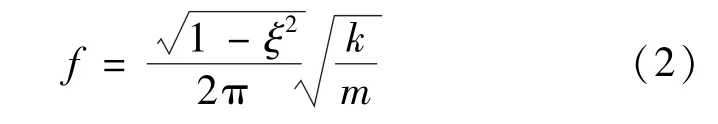
式中,ξ為阻尼系數,k為剛度,m為簧上質量。
計算得f=9.4 Hz,與圖4中的垂向振動頻譜特性的能量最大處一致,因此,車體的垂向振動能量主要來源于二系固有振動能量,可以認為垂向振動偏大的問題是二系剛度與軌道激勵的頻率不匹配所致。
4.2 車體橫向加速度
如圖6所示,圖6a為動力學仿真所得的車體座椅處橫向加速度的仿真值,圖6b為加速度的頻譜分析圖。
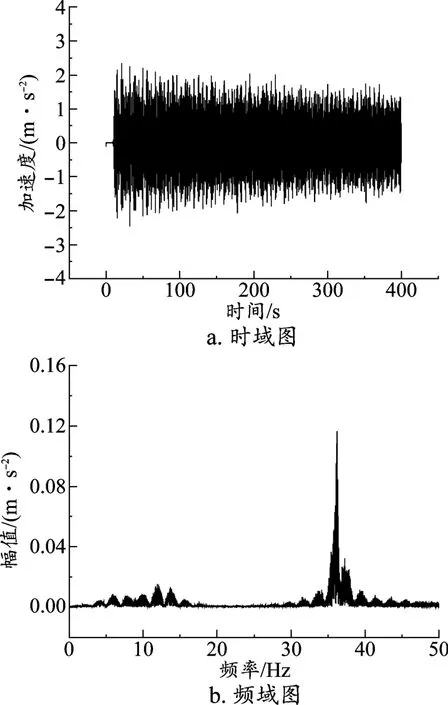
圖6 車體橫向加速度仿真值
如圖7所示,圖7a為在線路上試驗所測量得到的車體座椅處橫向加速度的實測值,圖7b為加速度的頻譜分析圖。
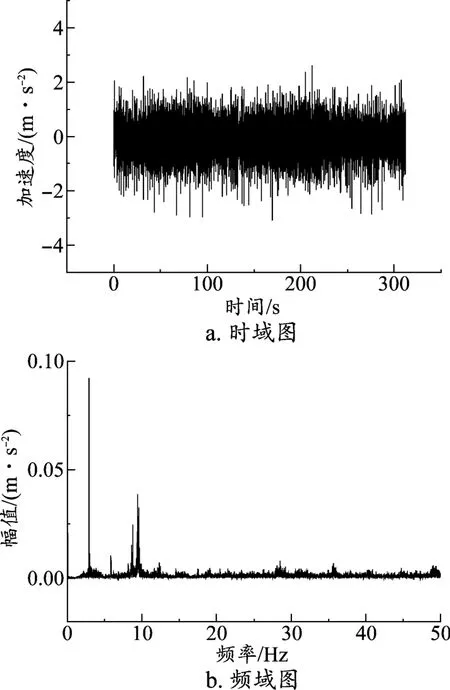
圖7 車體橫向加速度實測值
對比時域圖,車體橫向加速度的仿真所得最小值為-2.4 m/s2,最大值為2.3 m/s2,實測所得最小值為-3 m/s2,最大值為2.3 m/s2。
對比頻域圖,仿真所得的橫向振動在頻率為12、14、36 Hz處具有較大能量,實測所得的橫向振動在頻率2、9、29、36 Hz等處具有較大能量。
根據垂向加速度、橫向加速度的仿真值與實測值比較分析,仿真結果與實測結果接近,因此本文建立的動力學模型可以反映磁浮軌道巡檢車的垂向振動以及橫向振動特性,可以基于該模型進一步研究整車的動力學特性。
4.3 車輛平穩性改進
磁浮軌道巡檢車的高速巡檢功能需要盡可能高的巡檢速度,以利于減少巡檢時間,提高軌道檢測效率。而在工程試驗中發現,車輛的速度在超過20 km/h時,振動顯著變大,平穩性變差。論文分析了不同車速下的垂向平穩性指標,車輛在20~22 km/h以及15 km/h以下條件下運行垂向平穩性指標小于3,較為平穩,而超過20 km/h時,速度越快平穩性越差,最高運行速度在25 km/h以下。
為了改善該問題,提高車輛的平穩性,基于4.2節分析,本文采用改變二系剛度選調節二系的固有頻率的方法,避免車體振動與軌道激勵的頻率重疊,改善車體的振動。在比選市場常用減振器的基礎上,作者選擇了某二系的減振器,其垂向剛度為270 000 N/m。
分別以不同的速度對磁浮智能巡檢車整車進行動力學仿真,依據GB/T 17426標準對車體座椅處的垂向振動加速度值進行處理,分析整車的平穩性指標。將原減振器參數與改進選型后的減振器參數的計算結果進行對比,得到垂向平穩性指標進行如圖8所示。
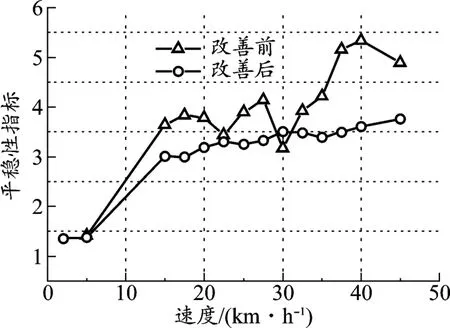
圖8 垂向平穩性指標與速度關系
由圖8可見,改善前車輛速度小于25 km/h時,平穩性指標在3.5~4以內,達到貨車平穩性良好的要求;在車輛速度25~35 km/h范圍內,平穩性指標在4~4.25以內,達到貨車平穩性合格要求;在超過35 km/h以后,平穩性指標不合格。
減振器選型改進后,車輛在0~35 km/h的速度區間垂向平穩性指標均小于等于3.5,可達到貨車平穩性優的指標。而在35~45 km/h的速度區間平穩性指標在3.5~4以內,達到貨車平穩性良好的要求。相較現有車輛相比可以顯著改善其平穩性,因此選型是合適的。
5 結論
(1)本文建立的磁浮智能巡檢車的動力學模型的仿真結果與實測結果的時域特性與頻域基本一致,證明了動力學模型的有效性。
(2)仿真發現當前車輛配置條件下車輛速度超過25 km/h時垂向平穩性變差。
(3)通過優化車架與車體間減振器參數,進行動力學仿真,結果表明新的減振器參數對車輛垂向平穩性有較大改善,可用于后期中低速磁浮軌道巡檢車改進。

