基于改進粒子群優化算法的太陽能發電系統無功優化
李旭炯,孫林花
(蘭州資源環境職業技術學院,甘肅 蘭州 730021)
0 引 言
近年來,太陽能(Photovoltaic Power,PV)發電無論從建設規模和入網數量都發展迅速。通常,太陽能從配電網側接入主網,導致配網結構由單源放射狀變為多源放射狀結構,原有單向潮流分布和負荷分布也會改變,造成無功功率不穩定,配網運行和控制更加復雜[1]。因此,配網無功功率優化是提高系統穩定性的有效措施。
本文以系統的有功功率為對應函數,考慮有功、無功以及電壓的約束,建模太陽能發電接入配網時無功功率優化模型,提出改進粒子群算法(Improved Particle Swarm Optimization,IPSO),在迭代中慣性權系數線性減小。最后依托IEEE 33系統仿真分析,驗證其可行性。
1 帶太陽能發電的配網無功優化模型
1.1 目標函數
從配網經濟運行的角度出發,對應函數設定為使有功損耗達到最小:
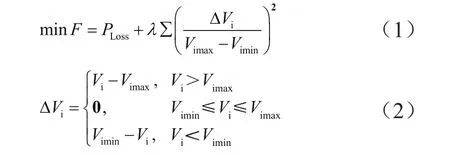

1.2 約束條件
平等約束條件為:

式中,Pi、Qi、Vi分別代表有功功率、無功功率、節點i的電壓,Gij、Bij、δij分別代表電導、電納、節點間的相位角差。
不等式約束條件為:

式中,Vi為節點i電壓幅值,Vimin、Vimax為節點i電壓幅值的上下限,Qi為太陽能發電系統無功輸出,QGimax、QGimin為太陽能發電系統無功輸出的上下限,Qimax、Qimin為系統無功補償設備容量的最大、最小值。
2 慣性權系數線性動態變化的PSO
2.1 IPSO
IPSO是對簡化社會模型的仿真而發展起來的。該算法特點如下[2]:
(1)基于魚群和鳥群這些群體性動物的研究;
(2)計算時間短,所需存儲量少。
IPSO搜索過程可描述為:一群粒子優化某一個特定的目標函數,且每個粒子都知道各自的最佳值(體極值)和坐標,此外每個粒子也知道其在組群中的最佳值(全局極值),也就是組中目前為止的最優值。利用當前速度及與體極值與全局極值的距離,可以得出每個粒子的修正速度,表示為:

式中,為迭代k時粒子i的速度,為粒子i的修正速度;rand為0~1的隨機數,為迭代k時粒子i的當前位置,pbesti為粒子i的體極值,gbesti為粒子i的全局極值,wi為粒子i的速度權函數,ci為每一項的權重系數。
本文在迭代過程中采用慣性權系數w由0.9線性減小到0.4的措施,式(5)中函數的系數w設為如下方程:

式中,wmax=0.9,wmax=0.4,itermax為最大迭代數,iter為當前迭代次數。
搜索過程中,慣性權重因子呈線性遞減的趨勢,開始時,w最大,對應的整體搜索能力也表現最強,能夠很快地定位最優解。迭代后期,w逐漸減小,對應的部分搜索能力得到了提高,可準確地確定最優解的位置[3]。
2.2 程序設計及算法流程圖
IPSO的實現步驟如下:
第一步,利用初始化參數(種群數量、粒子數目、迭代次數以及慣性權重因子),隨機生成粒子的初始搜索點和速度;
第二步,每個粒子搜索點損耗由潮流計算得到,如違反約束,在損失基礎上增加懲罰;
第三步,將體極值設為每個初始搜索點。將體極值中的初始最優評估值(損失加懲罰)設為全局極值;
第四步,計算新速度,連續變量采用連續方程,離散變量采用離散方程;
第五步,計算新搜索點,連續變量采用連續方程,離散變量采用離散方程;
第六步,計算新搜索點和估計值的損耗;
第七步,如果每個粒子的估算值優于之前的值,則將這個值設為體極值,如果最優體極值優于全局極值,將此值設為全局極值,存儲所有全局極值作為最終控制策略的候選值;
第八步,如果迭代數達到最大值則修正,否則回到第四步。
結合潮流計算,整個潮流優化程序流程如圖1所示。

圖1 算法流程圖
3 實例分析
為驗證所提算法可行性,依托融合太陽能發電系統的IEEE 33節點系統,通過如下的3種方案仿真分析,并進行了比較。
方案1,電流系統中不存在用于無功補償的設備,太陽能發電系統的無功調節也忽略不計,結構如圖2所示。

圖2 IEEE 33節點系統
方案2,不管太陽能發電系統的無功調節能力有多強,只通過無功補償裝置來調節無功。因為并聯電容器安裝節點越靠近線路末端,配電網損耗越小,網損優化效果也越好。因此,選取第24號和32號節點作為并聯電容器組的接入點,每組電容器為50 kvar,可補償配電網中的無功功率。表1為方案2接入節點及并網設備參數表。

表1 方案2接入節點及并網設備參數表
方案3,同時接入無功補償裝置和太陽能發電系統,系統無功功率由太陽能發電系統和無功補償裝置調節。太陽能發電系統輸出有功功率為Pact=400 kW,無功功率輸出的最大值為|Qmax|=184 kvar,假設節點10和17為太陽能發電系統的接入點。表2為方案3接入節點及并網設備參數表。

表2 方案3接入節點及并網設備參數表
通過Matlab仿真,得到3種方案的損耗和最小電壓。3種方案的節點電壓對比如圖3所示。
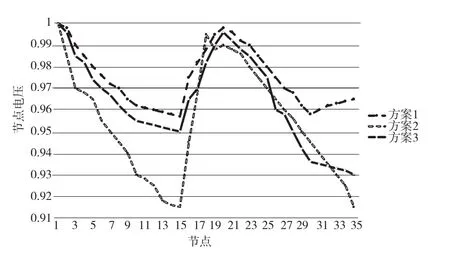
圖3 3種方案的節點電壓對比
可以看出,方案3既包含無功補償裝置,又融合了太陽能發電系統的無功功率,優化結果最好,節點電壓支持能力最強,系統有功損耗最小。已知每個電容器組容量值是50 kvar,因此方案2中,兩個無功設備的電容組數為11和16,而方案3中,兩個無功設備的電容組數為10和12。適當增加太陽能發電設備可降低無功設備的投資,節約運行成本。
4 結 論
本文通過太陽能發電系統本身的無功功率調節能力,針對每個節點約束,建立了太陽能并網配電網無功優化模型。通過引入動態慣性權值因子改進傳統PSO,解決以往算法不能將整體和部分搜索能力一同兼顧的問題,通過計算機仿真分析,獲得了優化結果。結果表明,太陽能發電并網接入配網,可減少無功補償設備的投入,節約運行成本。通過基于IPSO的無功功率優化,可有效降低系統的損耗,提高系統運行的穩定性和適應性,實驗結果說明了該算法在優化系統無功中的有效性。

