Φ273管道的電磁勵磁仿真模型分析與實驗方法*

楊理踐， 徐 龍， 高松巍

(沈陽工業大學 信息科學與工程學院， 沈陽 110870)

當今世界能源運輸愈發重要，油氣管道作為一種特殊載體對于長距離運輸石油、天然氣等重要能源物資具有無法替代的作用.漏磁檢測作為無損檢測技術的一種，被廣泛應用于長輸油氣管道缺陷在線檢測[1]，對于在役油氣管道的金屬缺陷及裂紋異常檢測具有一定的效果[2]，該技術突出優勢在于效率高、可靠性高及檢測成本較低.

隨著科技的逐漸發展，漏磁檢測技術日趨成熟.日本學者Nara等[3]實現對管道缺陷的精確識別，并研究漏磁信號從時域到頻域的過程；韓國學者Hui等[4]在三維軸向裂紋的研究分析中采用了有限元的方法；馮健等[5]提出了基于神經網絡的漏磁信號模式識別技術；黃作英等[6]應用磁荷法確定漏磁信號的數學模型；彭麗莎等[7]對管道缺陷重構方法進行研究；楊理踐等[8-10]以工程應用中的管道漏磁檢測系統為基礎，研究漏磁場缺陷信號的各種特征，并嘗試將剩磁效應應用在管道檢測中，分析了漏磁檢測信號的影響因素及永磁勵磁的磁路優化.

本文提出了一種適用于管道漏磁內檢測技術的電磁勵磁方式，依據永磁體模型參數及產生磁場特點探求具有相同磁化效果的電磁勵磁磁路模型，對比分析管道缺陷在不同磁路特征下所表現的特性，并構建仿真模型與實驗數據之間的關系，從而建立準確的磁回路仿真模型.

1 油氣管道漏磁內檢測技術

長輸油氣管道一般由高磁導率的鐵磁性材料加工而成，檢測之前需要經勵磁裝置磁化，磁化主要包括電磁勵磁和永磁勵磁兩種，它們產生能量的方式不同，磁路結構也存在一定區別，需要根據實際情況做出合適的選擇.

1.1 永磁勵磁的磁路模型

永磁勵磁方式在漏磁檢測中應用較為廣泛，在無缺陷時，磁感應線會在管道內部平行且均勻通過，理想情況下泄露的磁通量基本為零；當表面或近表面存在缺陷時，磁感應線受到阻隔發生畸變，部分磁感應線會泄露到空氣中，產生的漏磁通會形成漏磁場，其檢測基本模型如圖1所示.

圖1 永磁磁勵的磁路模型Fig.1 Magnetic circuit model for permanent magnetic excitation

1.2 電磁勵磁的磁路模型

以永磁勵磁模型為基礎，鐵芯上繞制匝數為N、激勵電流為I的線圈，通過調整參數實現最佳磁化效果，磁路模型如圖2所示.

圖2 電磁勵磁的磁路模型Fig.2 Magnetic circuit model for electromagnetic excitation

電磁勵磁的磁路有兩部分，由于模型完全對稱，可認為兩個部分的磁回路均分能量.取其中一個磁路，由鐵芯、鋼刷、軛鐵和氣隙串聯而成.

磁路計算時，通常將磁路分為兩部分：一部分為鐵芯，截面積為Sm，長度為Lm，磁場強度為Hm，磁感應強度為Bm；另一部分為氣隙，截面積為Sδ，長度為Lδ，磁場強度和磁感應強度分別用Hδ、Bδ來表示.

根據安培環路定理可知

F=HmLm+HδLδ=IN

(1)

式中，F為整個電磁鐵的磁通勢.

根據所建立的磁路模型，可以求得該磁路的磁通Φ為

(2)

式中：Rδ為氣隙磁阻；R1為導磁材料磁阻；R2為管道磁阻.若僅考慮氣隙磁阻，則

(3)

將式(2)改寫為

(4)

式中：μ0為空氣磁導率；w為磁路的寬度；h為磁路徑向有效長度.

氣隙的磁感應強度Bδ為

(5)

由式(5)可知：影響磁路氣隙磁感應強度的主要因素不但包括線圈的匝數、電流值的大小，還有氣隙長度.

管壁截面處的磁感應強度為

(6)

由安培環路定理得電磁鐵的磁感應強度為

(7)

當電磁鐵幾何參數固定時，管道中某一點的磁感應強度大小與線圈匝數、激勵電流具有密切關系，為建立仿真分析提供了理論基礎.

2 電磁場磁路分析

在實際工程應用中，電磁場中偏微分方程的求解是一個極其復雜的過程，并且只有少數的場問題能夠得到解析解，需要使用其他的計算方式來進行求解.

2.1 漏磁場計算的數值法

對于電流密度J在磁導率為μ的介質中所形成的磁場強度與磁感應強度的關系，可由磁通連續性原理與全電流定律獲得，即

(8)

由于磁感應強度法向連續，磁場強度切向連續，引入磁位A為

×A=B

(9)

理想管道結構周向完全對稱，矢量磁位只有一個分量，則控制方程為

(10)

采用柱坐標系進行分析可知

(11)

可以求得磁感應強度為

(12)

(13)

式中：r為徑向參數；Br為磁感應徑向分量；Bz為磁感應軸向分量.

2.2 三維有限元分析方法

有限元分析的基本思想是利用離散化數值求解，由麥克斯韋方程組推導出磁場的偏微分方程為

(14)

式中，ε為介電常數.引入的矢量磁勢滿足

(15)

利用變分法將三維靜態磁場用標量形式泛函表示得

(16)

式中，P為中間量，其值為

P=AxJx+AyJy+AzJz

(17)

對式(17)進行離散分析，磁位A轉換為直角坐標系并引入x，y，z三個分量，對磁位求偏導，化簡為

(18)

式中：K為剛度矩陣；f為激勵.

3 電磁勵磁模型有限元仿真

建立Φ273(壁厚約為6.8 mm)管道電磁勵磁模型，分析管道在達到近飽和狀態下線圈匝數及激勵電流參數，并分析缺陷特性.模型的具體幾何尺寸如表1所示.

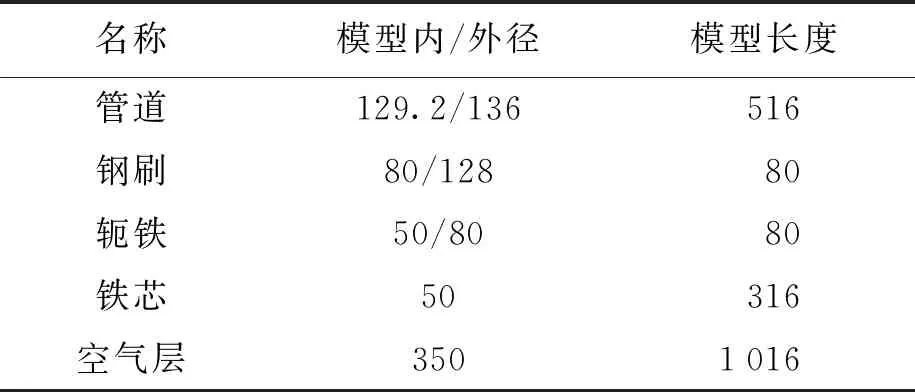
表1 電磁勵磁仿真模型各部分幾何尺寸Tab.1 Geometry of various parts of electromagnetic excitation simulation model mm

3.1 COMSOL有限元仿真軟件及仿真流程

COMSOL是一款應用廣泛的高級數值仿真軟件，優勢在于多物理場耦合，本文主要以有限元法為基礎，通過對偏微分方程的求解來實現真實物理現象的仿真.幾何建模后，由于模型中各部分的材料功能不同，部分材料屬性需要自定義.

管道選用X52鋼，軛鐵選用Q235鋼，是一種普通碳素結構鋼，屈服值大約為235 MPa，綜合性能較為優越，應用范圍廣泛.對于鋼刷的介質描述十分困難，磁特性接近線性，本文設定磁導率為7.需要注意的是，上述的幾種材料均為各向同性.

網格劃分的形狀和疏密程度將會在很大程度上影響最后的計算結果，本文采用智能網格劃分方式，對于管道還需要進行局部網格細化.

軟件會自動將模型電磁鐵電流加載到模型上，不需要施加其他載荷.此外，空氣層要達到一定程度來模擬遠場邊界的約束條件.經過穩態求解器計算，利用軟件提供的結果通用處理器可以查看磁通密度分布云圖、磁感應圖、磁場等值圖及各種矢量圖.

3.2 模型參數優化

電磁勵磁模型中的參數包括線圈匝數、激勵電流大小、線徑以及線圈的體積等，它們都會對產生的磁化能量有著或多或少的影響，在設計和使用時需要調整.已知無缺陷管道外壁點C處磁通密度約為10 mT，以此為基準進行參數優化，考慮到激勵電流不宜過大(這里選用0.3 A的激勵電流)，不同線圈匝數模型所表現出來的磁通密度分布云圖如圖3所示.

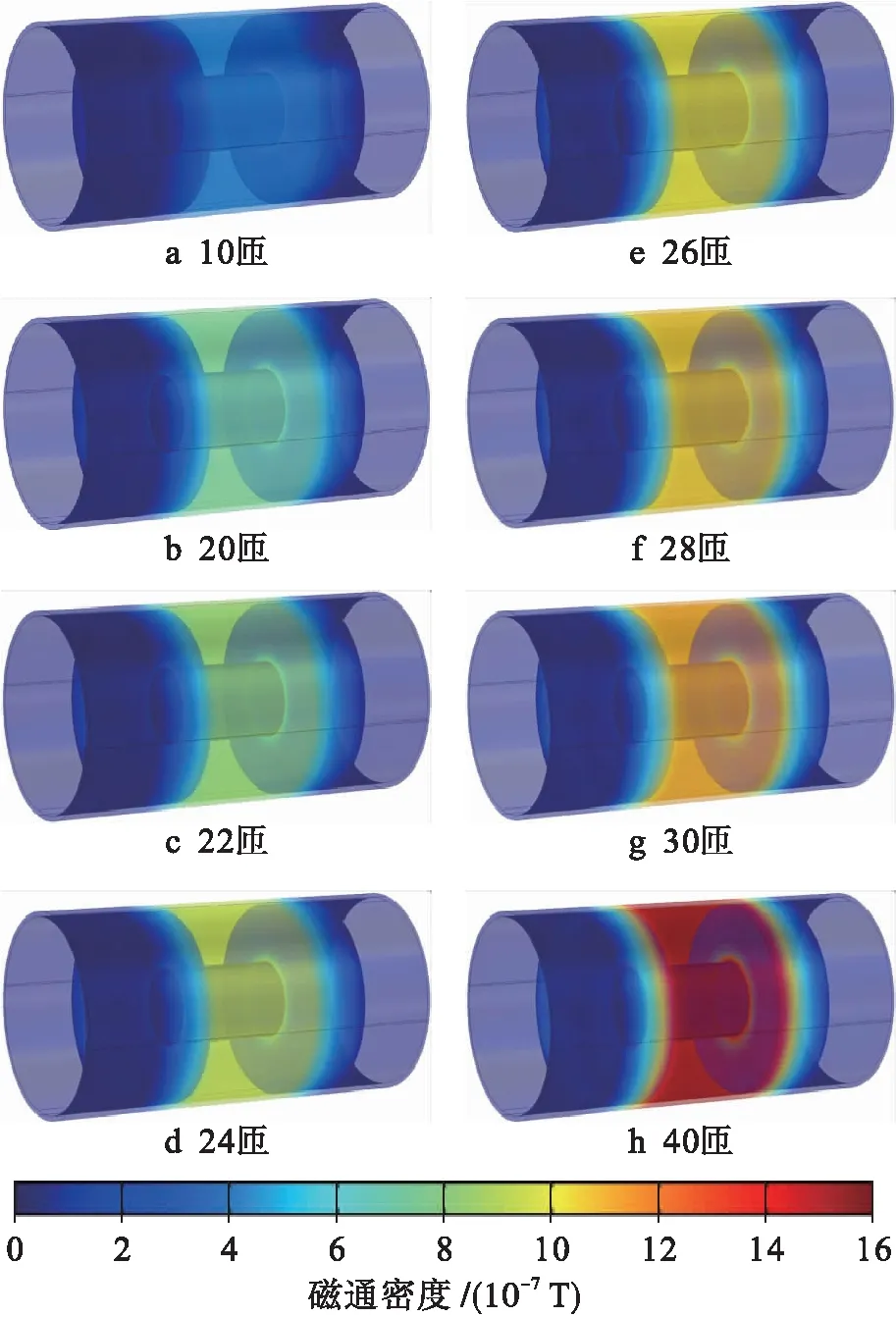
圖3 不同線圈的仿真模型磁通密度云圖Fig.3 Magnetic flux density nephogram of simulation model for different coils

由圖3可知：隨著線圈匝數的增加，管道中間的局部磁化區域能量逐漸增強.當線圈匝數少于20匝時，管道的磁化程度未達到要求；當線圈匝數超過30匝時，管道達到過飽和狀態，不符合實際中的檢測要求.選取其中線圈匝數為20～28匝的模型，通過路徑映射的方式測量管道外壁軸向磁通分量的具體數值，測量結果如圖4所示.

仿真結果分析可知：隨著電磁鐵中線圈匝數增加，C點處軸向磁通分量會逐漸變大.當電磁鐵中的線圈匝數接近26匝時，軸向磁通分量為10.046 mT，誤差為4.6%.

3.3 不同徑向深度缺陷特性分析

在電磁勵磁模型中，線圈匝數為26匝，激勵電流為0.3 A，選用軸向長度為40 mm、周向寬度為20 mm、徑向深度分別為1.3、1.8、2.4、4.0 mm的缺陷進行分析，不同徑向深度缺陷的徑向磁通分量曲線如圖5所示.

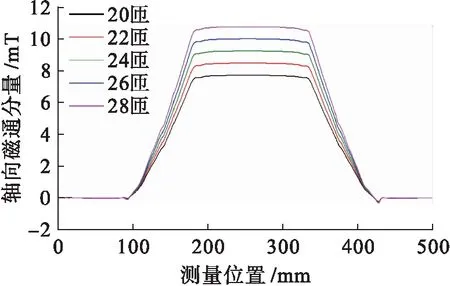
圖4 不同線圈匝數下C點的軸向磁通分量Fig.4 Axial flux component at point C under different coil turns

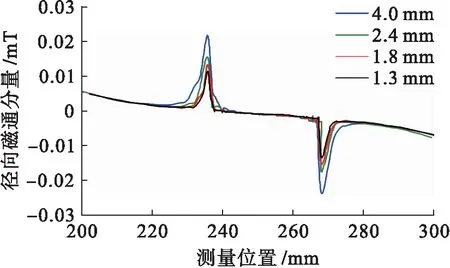
圖5 不同徑向深度缺陷的徑向磁通分量Fig.5 Radial flux components of defects with different radical depths

由圖5可見，在缺陷的中心處位置，徑向磁通分量數值較小，接近于零；在缺陷的兩側邊緣位置，徑向磁通分量會達到峰值點；隨著缺陷的徑向深度增加，徑向分量的峰值逐漸變大，峰值隨缺陷徑向深度增加分別為0.013 3、0.013 5、0.014 4、0.021 9 mT.

3.4 不同軸向長度缺陷特性分析

選用周向寬度為40 mm、徑向深度為1.8 mm、軸向長度分別為10、20、40 mm的缺陷進行分析，徑向磁通分量曲線如圖6所示.

圖6 不同軸向長度缺陷的徑向磁通分量Fig.6 Radial flux components of defects with different axial lengths

由圖6可見，隨著缺陷長度增加，徑向分量的峰峰值間距增大；在缺陷的中心位置，徑向分量接近于零；在缺陷的邊緣位置，由于磁力線集中，徑向分量會達到峰值.

4 實驗與結果分析

根據工程中漏磁內檢測裝置所檢測的結果，研究不同磁路特征的漏磁信號曲線特性及磁感應強度分布特點，探求工程實驗與電磁鐵仿真之間的聯系與區別.

4.1 實驗裝置

采用Φ273管道漏磁檢測裝置進行拖拉實驗，其中漏磁內檢測裝置在管道中運行，主要分為動力節、磁化節(參數與電磁勵磁仿真模型完全相同)、計算機節和電池節，各部分協同工作.實驗裝置的結構如圖7所示.檢測裝置中磁敏探頭元件為包含數字輸出的三軸霍爾傳感器MLX90393，可以檢測到1 050 mT的磁場強度.

圖7 管道漏磁內檢測器結構Fig.7 Structure of internal detector for pipeline magnetic flux leakage

4.2 實驗結果

檢測到的漏磁場信號被存儲到計算機節進行初步處理，待拖拉實驗結束后，將數據導入專用上位機軟件，得到軸向凹溝3個探頭所采集的徑向磁通密度數據，如圖8所示，每條曲線代表一個探頭的數據.

由圖8可見，隨著深度的增加，徑向磁通分量峰值逐漸變大，驗證了仿真結果的形態趨勢.深度為1.3、1.8、2.4、4.0 mm時，3個探頭峰值均值分別為2.38、3.28、4.62、8.33 mT.從峰值的均值數據上可以看出：經歸一化深度每增加0.1 mm，其徑向磁通分量的峰值增加約0.16 mT，呈線性關系.

綜上所述，永磁勵磁實驗裝置與電磁勵磁仿真模型在不同磁路特征下表現出相同的磁路特性，驗證了以電磁勵磁模型替代永磁勵磁模型進行分析的有效性，證明電磁勵磁仿真模型對永磁磁路優化具有指導意義.

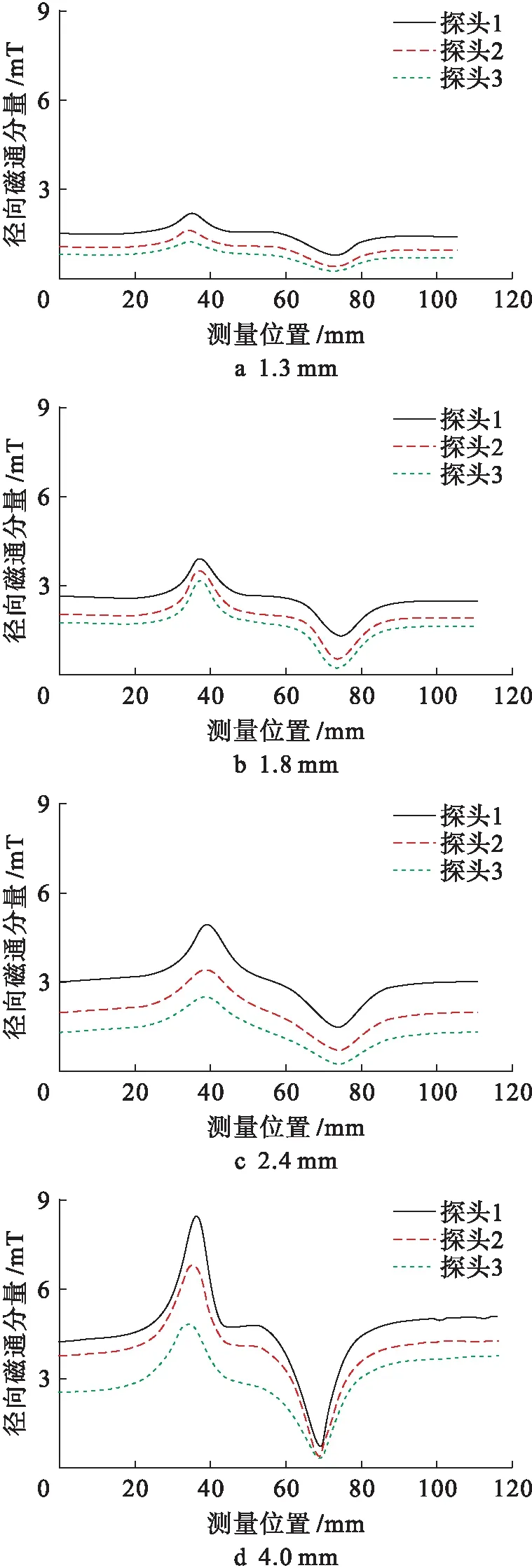
圖8 不同深度缺陷的徑向磁通數據曲線Fig.8 Radial magnetic flux data curves of defects with different depths

5 結 論

通過仿真與實驗的對比分析，結合工程電磁場理論，得出以下結論：

1) 相同模型尺寸下，調整電磁鐵參數可使電磁勵磁與永磁勵磁具有相同的磁化效果.

2) 電磁勵磁對于不同磁路特征所表現出來的特性具有相同的形態趨勢，證明了從電磁場角度來分析永磁磁路的可行性.

3) 由理論計算得知：電磁勵磁仿真結果與工程中永磁勵磁結果之間存在線性比例關系，說明可以從電磁場角度建立準確的漏磁檢測仿真模型.