基于模型預測控制的車道保持策略研究與應用
蔣立偉 檀生輝 吳 勇
(西安電子科技大學蕪湖研究院,安徽蕪湖241000)
1 車輛動力學模型的建立
首先,在如下假設的前提下,建立車輛的二自由度動力學坐標系和模型,如圖1所示:(1)不考慮車輛在Z軸方向的運動,只考慮在X、Y水平面的運動;(2)左、右側車輪轉角一致;(3)車輛行駛速度變化緩慢,忽略前后軸載荷的轉移;(4)車身及懸架系統是剛性的;(5)轉向時轉角直接輸入給轉向輪。
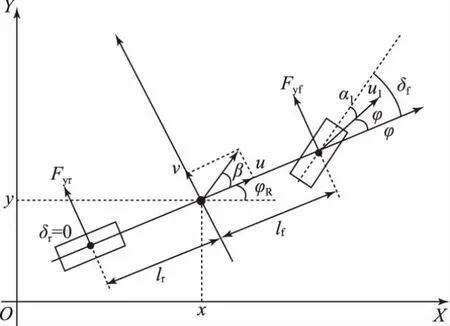
圖1 車輛的二自由度動力學坐標系和模型
然后,按如下3個步驟建立車輛動力學模型:
(1)確定汽車質心絕對加速度在車輛坐標系上的分量ay:
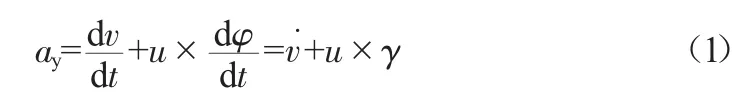
式中:v為車輛沿y軸的速度;u為車輛沿x軸的速度;φ為車輛橫擺角(偏航角);γ為橫擺角速度。
(2)確定車輛受到的側向力∑Fy和橫擺力矩∑Mz,前角轉向δf很小,后角轉向δr=0。
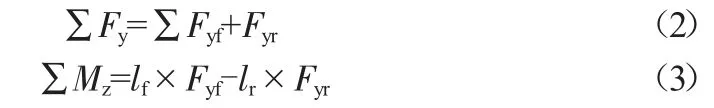
式中:lf、lr分別為前后軸到質心的距離。
前、后輪側偏力為:

式中:k1、k2分別為前后輪側偏剛度;αf、αr為側偏角。
由上述公式得到前后輪側偏角:
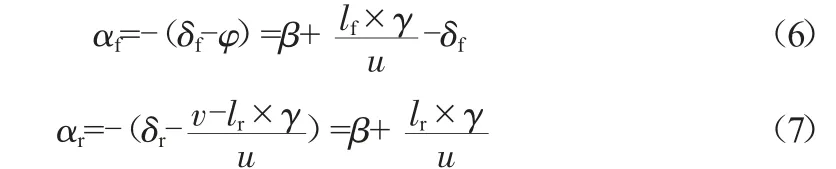
式中:β為質心側偏角;φ為車輛橫擺角(偏航角);δf為前角轉向;δr為后角轉向;γ為橫擺角速度。
(3)建立外力、外力矩與汽車運動參數的關系及運動微分方程:
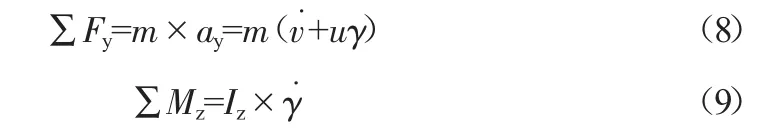
式中:m為整車質量;Iz為車輛繞過質心垂直軸線的轉動慣量。
將式(6)~式(9)整理后得到車輛動力學模型如下:
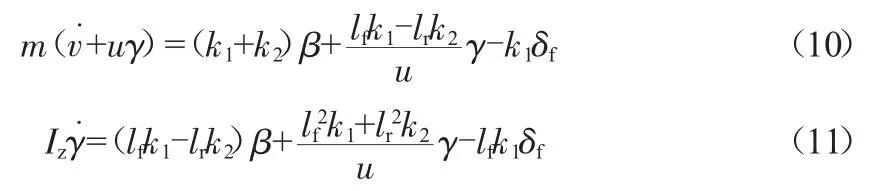
在車輛動力學的基礎上,還需建立側向偏差y、航向角偏差φ和動力學方程之間的關系,車輛運動與道路關系模型如圖2所示。
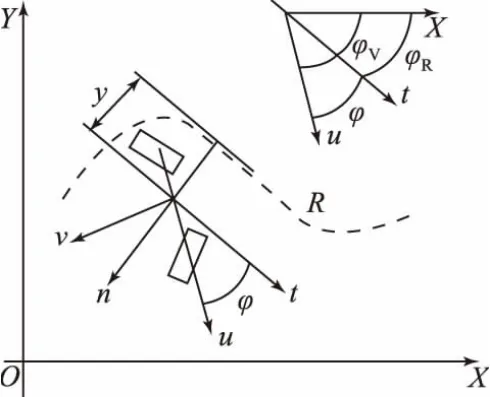
圖2 車輛運動與道路關系模型
其中,φR為道路航向角;φV為車輛航向角,聯合式(10)、(11)建立系統的狀態方程如下:
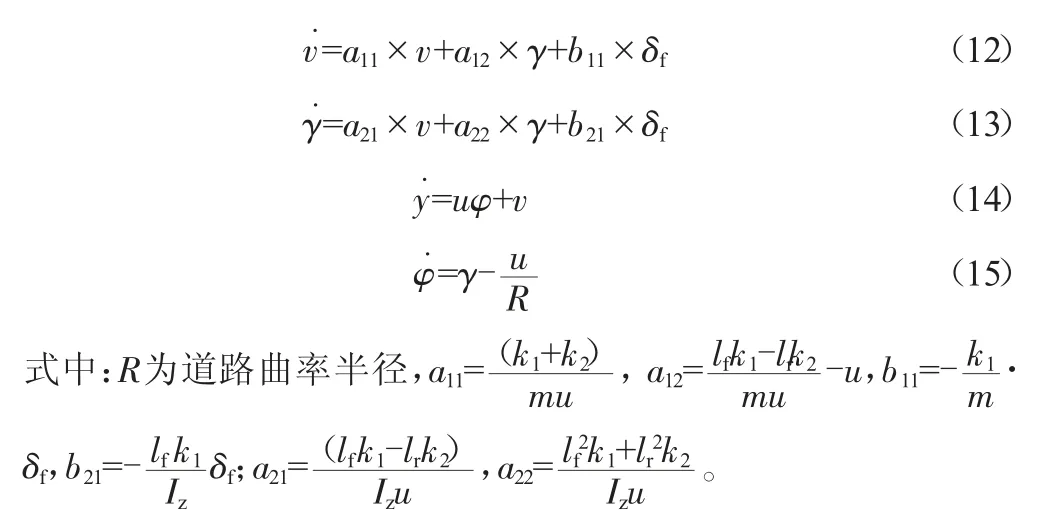
進一步整理得:

其中:
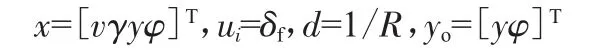
定義:狀態變量為側向速度v、橫擺角速度γ、側向偏差y、航向角偏差φ。控制輸入為前輪轉角δf,已知輸入為道路半徑R。
2 基于模型預測控制的車道保持策略建模
基于模型預測控制車道保持策略主要包含:模型預測、滾動優化和反饋矯正、目標橫向偏差、橫擺角偏差控制模塊和縱向控制模塊。
車道保持是通過檢測車輛與道路中心線的橫向偏差和橫擺角偏差來控制車輛的方向盤的轉角,最終使車輛行駛在道路中心線上,其中所用的車輛參數整車質量m=1 270 kg,繞Z軸轉動慣量Iz=1 536.7 kg·m2,前后軸距lf、lr分別為1.015 m、1.895 m,前后輪側偏剛度k1、k2都為180 000 N/rad。
2.1 模型預測
模型所需相關的參數如下所示:
將上一章節中的狀態方程模型式(16)(17)進行離散化,得到:
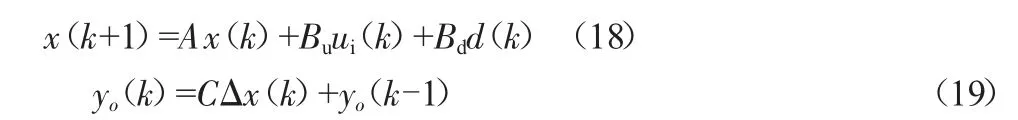
以最新測量值為初始條件,預測時域為p,控制時域為m,得到:Δx(k+1/k)=AΔx(k)+BΔui(k)+BdΔd(k),表示第k個時刻對第k+1個時刻的狀態預測,進一步輸出方程為:
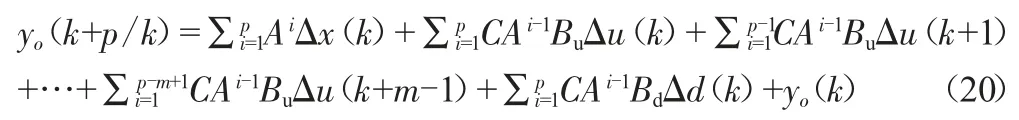
那么,對系統未來p步預測的輸出為:
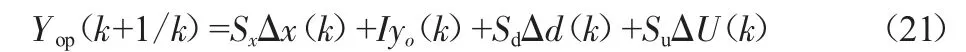
2.2 滾動優化模型
得到車輛模型在預測時域內的預測輸出后,建立模型預測輸出與期望輸出之間的偏差和控制量及其變化率的二次型目標函數,具體如下所示:
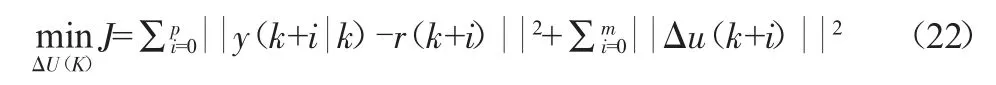
其約束條件為:
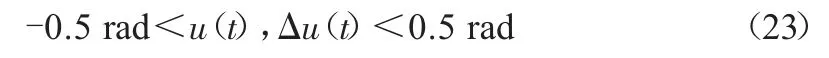
其中,y(k+1)為目標參考序列,即期望的目標橫向偏差和橫擺角偏差序列,可通過對狀態方程(14)(15)積分得到,作為控制模型的輸入,如圖2所示。通過二次規劃的方法可以求解出最優的控制量即前輪偏角。最后通過在每個控制周期不斷地求解最優的控制量,形成滾動優化過程。
2.3 反饋矯正
反饋矯正是通過比較模型輸出與實際對象輸出之間的偏差來修正模型的預測輸出。
2.4 目標橫向偏差和橫擺角偏差模塊
作為目標參考序列的期望的目標橫向偏差和橫擺角偏差序列,可通過對狀態方程積分得到作為控制模型的輸入,如圖2所示。
2.5 縱向控制模塊
縱向控制是對設定的目標車速進行PID閉環控制,使車輛保持穩定車速行駛。
3 整車Carsim模型搭建
首先,根據整車參數搭建整車模型,如圖3所示,然后根據控制需求添加接口,整車的輸入接口包括方向盤轉角、節氣門開度和制動壓力,輸出接口包括縱向速度、橫向速度、橫擺角速度、道路曲率。設計道路模型,包括直道、半圓道、正弦道,總計3.9 km。
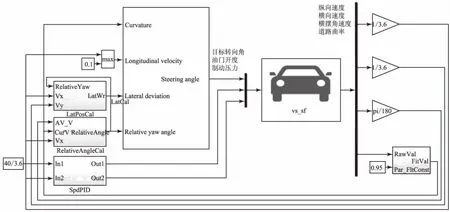
圖3 車道保持模型在環仿真系統
4 控制模型與整車模型集成測試
4.1 模型在環仿真測試
將第2節開發的基于MPC的車道保持控制模型與第3節搭建的整車模型在Matlab/Simulink環境中進行集成和聯合仿真測試。
模型開始運行后,車輛以40 km/h的車速在道路上勻速行駛,仿真結果如圖4所示。
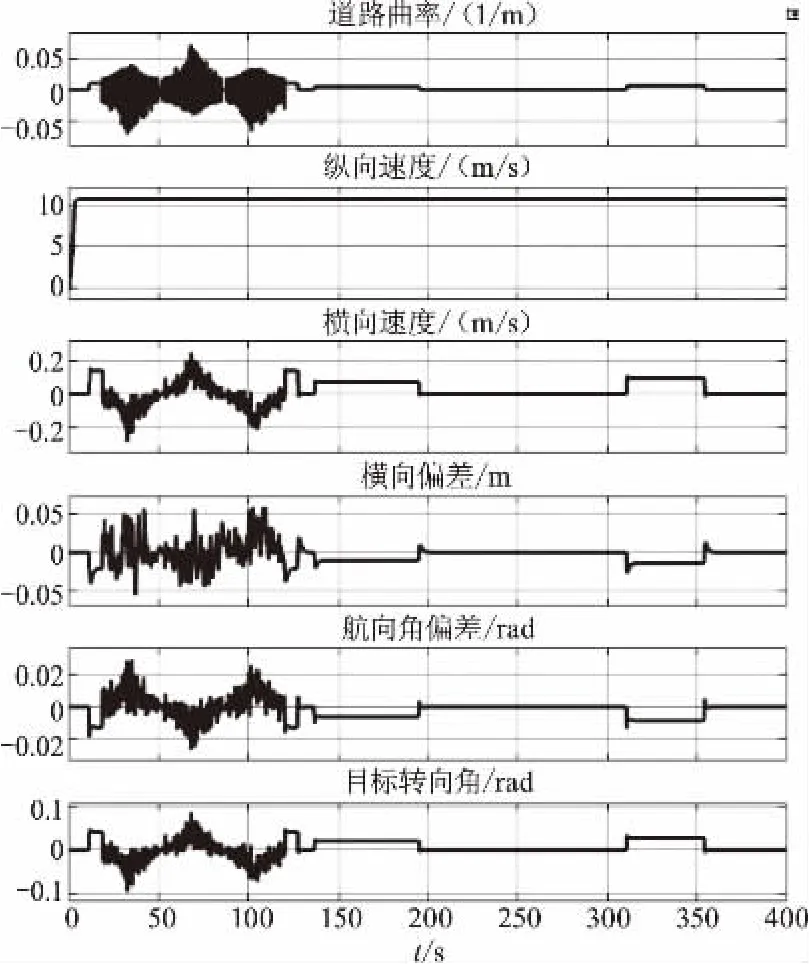
圖4 車道保持控制系統過程數據
從圖4過程數據可以看到,車輛開始從直道上行駛至10.5 s變為彎道,到18.2 s后變為正弦道路,由于車輛檢測到道路曲率的變化,目標轉向角根據道路曲率開始調節,使車輛保持在道路中心位置,在此過程中,道路曲率、橫向速度、側向偏差、航向角偏差也隨之平穩變化,直到120 s后又進入彎道,如此按照預定的道路行駛,直到行程結束。
在整個行駛過程中,最大側向偏差不超過6 cm,目標方向盤轉角在-0.1~0.1 rad內平穩變化,滿足約束條件。基于MPC的車道保持控制效果如圖5所示。
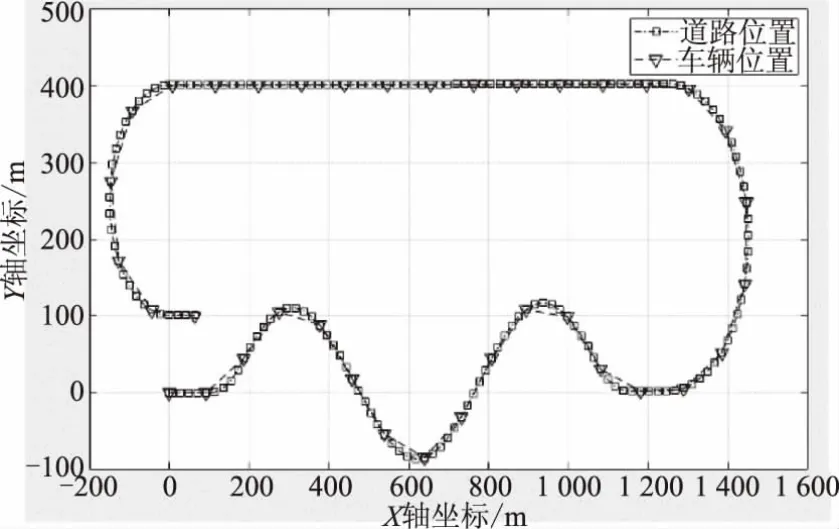
圖5 基于MPC的車道保持控制效果
從圖5的控制效果可以看到,通過基于MPC的車道保持控制,車輛的位置曲線和道路的位置曲線能高度重合,即較好地實現了車道保持控制。
4.2 實車道路測試
將圖3中浮點的控制模型通過定點化和接口配置之后,生成C代碼與嵌入式處理器的基礎軟件集成、編譯,并將可執行文件刷寫到ADAS ECU中運行,車道保持實車測試結果如圖6所示。
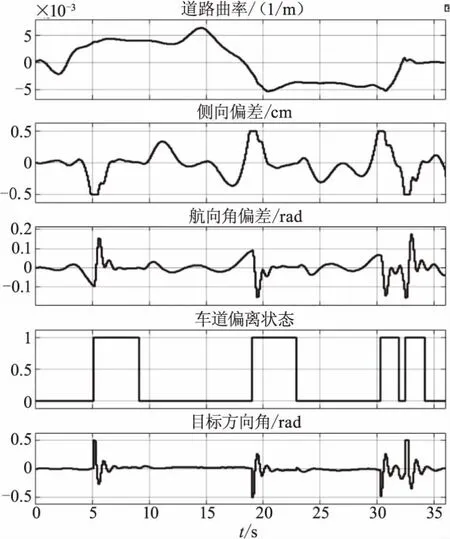
圖6 車道保持實車測試結果
控制模型輸入所需的道路曲率、車輛航向角等信號,通過CAN總線從感知信號處理的域控制器獲取,同時將目標轉角控制指令發送給電動助力轉向控制器執行,實現車道保持。如圖6所示,車輛在行駛過程中,運行基于模型預測控制的車道保持策略的ADAS ECU綜合道路曲率、航向角偏差和側向偏差,給出車道偏離狀態,并根據車道偏離狀態對轉向系統進行快速控制。在整個試驗過程中,最大側向偏差不超過5 cm,轉向角控制量超調較小且快速達平穩狀態,使車輛始終保持在道路中間位置行駛。
5 結語
本文針對輔助/自動駕駛車道保持系統,提出了一種基于模型預測控制(MPC)的車道保持控制策略。在車輛動力學和狀態方程的基礎上,開發了基于模型預測控制的車道保持控制策略,并與整車模型進行集成以及模型在環仿真測試,之后通過代碼生成和集成,將控制策略刷寫到實際ADAS ECU中進行實車道路測試、驗證和應用,試驗結果表明,在各種道路環境中,該控制策略始終能使車輛保持在道路中間行駛,具有良好的控制效果,提高了車輛的操縱穩定性,保證車輛行駛的安全性和舒適性。

