超高墩大跨連續剛構橋的受力分析

文/易嘉莉

1 前言

在推進中西部地區發展建設中，發現這些地區往往存在高海拔，多山地，地質地貌條件都較差，建設山區公路就需要一種高墩或超高墩大跨橋梁來克服同時可以很大程度保護環境，減少工程建設成本，但是隨著施工條件和外界環境的變化及建成后運營周期的增長，橋梁結構會發生改變，為了保證工程質量和人身安全必須對此類橋梁的受力特性進行分析研究。

本文在現有的研究成果基礎上，基于實際的工程案例結合相關理論對超高墩大跨連續剛構橋橋墩受力采用有限元軟件Midas-Civil 進行模擬分析，探究超高墩大跨連續剛構橋在收縮徐變影響下的橋墩受力特征，希望能為超高墩大跨度連續剛構橋設計提供參考價值。

2 受力方案設計

某橋梁位于西部山區的高度公路，主橋為預應力混凝土連續剛構橋上部采用（95+200+95）m 三跨一聯的結構，橋梁左右幅全長分別為870.5m 和1048.5m，單幅橋梁寬度為12.5m,橋梁全長395m，依據實際橋梁設計圖及說明，采用MIDAS-Civil 有限元軟件建立模型，模擬不同墩高組合對結構受力影響，其中1#墩，H1（153m），2#墩設置5 組數據，分別為H2（148m）、0.9H2（129m）、0.7H2（115m）、0.5H2（89m）及0.2H2（59m）。

3 收縮徐變對橋梁的受力影響

各種混凝土有不同的徐變和收縮特點，其主要取決于混凝土內部的水化泥漿的物理性質[1]，通常水灰比、水泥的用量、含水率、集料的種類、施工的溫度、水泥的品種等都會影響混凝土的收縮徐變[2]。運用有限元軟件，計算參數按照《公路鋼筋混凝土及預應力混凝土橋涵設計規范》（JTGD62—2004）取定，并根據模擬結果對收縮徐變影響因素進行分析。

收縮徐變作用下，不同墩高組合形式下墩底剪力值，見表1。

由表1 可知，假定保持1#墩的高度不變且改變2#墩的高度，1#墩墩底剪力和2#墩墩底剪力增大值在收縮徐變作用下，變化值相差不多，1#墩墩底和2#墩墩底的剪力都隨著2#墩高度的增大而減小，變化大致符合式（1），其中FS表示墩底剪力值，ΔH表示1#墩和2#墩的高墩差。

表1 收縮徐變：不同墩高組合形式下墩底剪力值

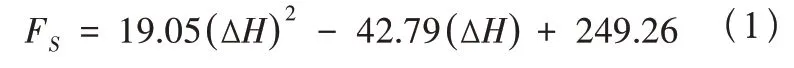
收縮徐變作用下，不同墩高組合形式下墩底彎矩值，見表2。

由表2 可知，在收縮徐變影響下，假定保持1#墩的高度不變改變2#墩的高度，2#墩的墩高增大反而使1#墩墩底的彎矩減小且墩底彎矩減小很顯著，1#墩墩底的彎矩從4.18E+04kN·m 增加到6.86E+04kN·m，增大的幅度約為64.4%，而2#墩墩底的彎矩對著2#墩的高度增大呈現出先增大后減小。

表2 收縮徐變：不同墩高組合形式下墩底彎矩值

收縮徐變作用下，不同墩高組合形式下墩底軸力值,見表3。

由表3 可知，在收縮徐變影響下，假定1#墩的高度不變且改變2#墩的高墩，2#墩墩高的變小同時引起2#墩墩底軸力減小，墩底軸力從2.80E+05kN 減小到1.65E+05kN，減少了約41.48%，其大致減小趨勢符合式（2），其中FN表示墩底軸力值;ΔH表示1#墩和2#墩的高墩差。

表3 收縮徐變：不同墩高組合形式下墩底軸力值

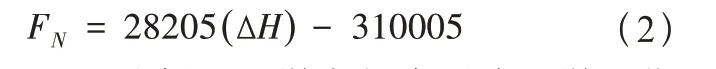
收縮徐變作用下，分析不同墩高組合形式下墩頂位移值。從模擬的結果分析得知在收縮徐變作用下，2#墩墩高減小帶動1#墩的左肢和右肢的墩頂位移在增大，而2#墩左肢和右肢的墩頂位移和2#墩墩高的變化保持相同的變化趨勢；隨著1#墩和2#墩高度差的增加，兩對稱薄壁墩頂位移的差值從0.9mm 增加到33m,增幅較大，可知隨著墩高高度差的增大，收縮徐變對橋墩有很大的影響，在設計橋梁結構時要引起重視。

4 墩高對橋梁的穩定性分析

通常連續剛構橋梁都會承受巨大的荷載，作為受壓構件的橋墩，隨著橋墩高度的增加，長細比也會增加，為提高結構穩定需要增大墩高，來保證施工階段和運營階段橋梁的穩定性。

當一個彈性體在外力作用下處于平衡狀態，系統外力位勢Πa和內力位勢Πi之和達到最小值，即總位勢最小，此時Π 一次變分為δΠ = 0，跟一般函數的極值類似。如果二次變分δ2Π ＞0,表示系統是穩定的，此時對應的位勢值極小；δ2Π = 0,表示此時系統是穩定平衡的；δ2Π ＜0 表示此時系統是不平衡的，對應的位勢值極大，系統是不穩定的。在橋梁上部結構的自身重量和施工的外力可以當作墩頂受到的集中力N，用q 表示墩身自重集度。

通常用來求解臨界荷載的方法是可得伽遼金（Galerkin)，其可用虛位移原理來證明壓桿平衡后的微分方程可以表示為：

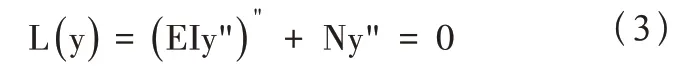
式（3）中：第一項表示內力形成的橫向荷載；后一項表示外力形成的橫向荷載。

由位移和力學邊界條件可知：

可得：

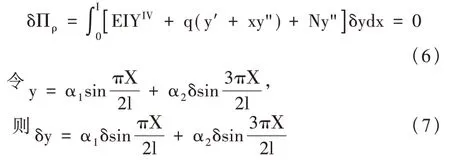
將式（7）代入式（4），得：

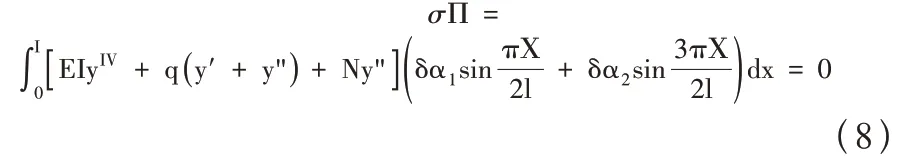
可得伽遼金（Galerkin)方程組

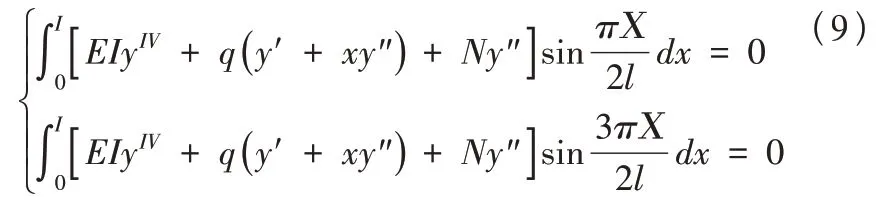
計算得臨界荷載：

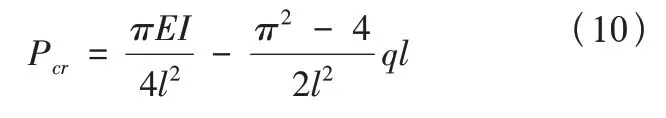
5 結語

綜上所述，建設山區公路需要應用高墩或超高墩大跨橋梁，本文基于實際的工程案例結合相關理論，分析了超高墩大跨連續剛橋的力學性能，計算表明，結構在各階段受力及穩定性都能滿足規范要求，建成后可為同類橋梁的施工積累經驗，具有參考意義。