聯動環支架間隙和數量對靜子葉片調節精度的影響
鄭 彥,鐘明橋
(中國航發四川燃氣渦輪研究院,成都 610500)
1 引言
喘振是由壓氣機的進、出口氣流通道和下游節流裝置等構成的整個壓縮系統的一種以氣流中斷為特征的不穩定狀態。當壓縮系統進入喘振時,其通過的流量以及壓氣機出口壓力等參數都隨時間做低頻振蕩[1]。為避免發生喘振,有效措施之一是調節壓氣機前幾級整流葉片的安裝角,使流入的氣流具有合適的迎角,避免氣流分離。在先進發動機上常采用多級可調靜子葉片(VSV)的方法使壓氣機的穩定工作范圍更寬,進而達到更好的防喘作用[2]。
國內,多位專家對航空發動機多級可調靜子葉片進行了理論和仿真研究。如賀飛等[6]采用齊次坐標分析法結合Matlab 軟件推導運動方程的設計方法,改進了模型航空發動機調節機構。胡明等[7]使用CATIA三維設計軟件和ADAMS虛擬樣機仿真軟件,設計了一種單級可調靜子葉片并對其進行仿真,驗證了設計的合理性,提高了設計效率。楊偉等[8]將ADAMS 參數化分析方法初步應用于高壓壓氣機調節機構設計。趙雷等[9]基于UG NX三維設計軟件和Excel 軟件對可調葉片運動機構進行了參數化拓撲仿真分析。楊永剛等[10]使用ADAMS 虛擬樣機仿真軟件對幾種搖臂和聯動環的連接結構進行了對比分析。胡文杰等[11]利用ANSYS 創建搖臂柔性體模態中性文件,并將柔性體導入ADAMS 中進行剛柔耦合動力學模型仿真分析,分析了搖臂的彈性變形對調節機構動力學特性的影響以及搖臂在調節機構阻力中的影響。但國內的研究多集中在剛體模型領域,研究對象的各個零部件不會發生彈性變形,無法評估多級可調靜子葉片運動過程中各個零部件的彈性變形對靜子葉片調節精度的影響。
為研究多級可調靜子葉片各個零部件的彈性變形對靜子葉片調節精度的影響,本文將聯動環先后設置為剛體和柔性體,使用ADAMS 虛擬樣機仿真軟件進行剛柔混合動力學模型仿真。利用UG NX創建三維CAD模型,再在ADAMS中創建運動副、驅動、載荷等模型要素,進行多體動力學仿真。
2 多級可調靜子葉片虛擬樣機的建立
多級可調靜子葉片虛擬樣機設計的主要要求是結構簡單、操作靈活,在完成規定角度范圍內轉角誤差小[12]。多級可調靜子葉片進行動力學仿真,需要各個部件的質量信息,因此需定義各個部件的材料屬性。將虛擬樣機模型導入ADAMS/View 中后,一旦給構件賦予了材料屬性,ADAMS軟件系統會自動計算出構件的質量、質心位置及構件的轉動慣量,并在質心處自動創建坐標系,進行運動學計算[7]。
2.1 VSV調節機構的組成
某型發動機的VSV 調節機構主要由可調靜子葉片、搖臂、聯動環、曲柄、連桿和作動筒等組成,采用外操縱方案。其外部零組件包括安裝在延伸機匣上的兩套液壓驅動組件,和安裝在高壓壓氣機外機匣上的曲柄、連桿、搖臂、聯動環等組件;內部零組件為高壓壓氣機機匣內部的進口導流葉片和可調靜子葉片。為簡化計算,忽略延伸機匣、銷子、銷軸、襯套、螺栓等零件。每級調節機構如圖1 所示。每級聯動環上有6個聯動環支架,沿聯動環周向均布。

圖1 VSV調節機構示意圖Fig.1 VSV adjustment mechanism diagram
2.2 VSV調節機構的機械原理
VSV調節機構的結構簡圖如圖2所示。調節原理是活塞桿在作動筒里做往復運動,帶動驅動臂、傳動桿和零級曲柄繞曲柄中心做定軸轉動。零級曲柄帶動零級聯動環做繞發動機軸線轉動和沿發動機軸線平動的復合運動。零級聯動環帶動零級搖臂,零級搖臂與進口可調導流葉片(IGV)固連,進口可調導流葉片繞自身軸心做定軸轉動。同時,零級曲柄帶動零一連動桿和零二連動桿,進而分別帶動一級曲柄和二級曲柄。類似地,第一、第二級曲柄分別通過帶動各自級的聯動環、搖臂,使第一、第二級可調葉片做定軸轉動。

圖2 VSV調節機構結構簡圖Fig.2 VSV adjustment system mechanism diagram
以IGV 級為例,各級零部件之間的運動副設置如表1 所示。為模擬襯套彈性變形,各級可調靜子葉片與各級內環的旋轉副用襯套力代替。

表1 模型約束類型Table 1 Model constraint types
2.3 模型載荷和驅動
VSV調節機構的動力學仿真不僅需要給模型添加各種約束,還要添加載荷和驅動。模型將葉片受到的氣動載荷分解為葉片繞自身的扭矩、沿發動機軸線的軸向力和沿轉子葉片旋轉方向的切向力。模型初始狀態下,各級可調靜子葉片處于中間位置,需要先將葉片復位。模型驅動方式為活塞桿強制位移驅動,總行程用時20 s。前5 s 模擬機構復位過程,活塞桿在空載下從中間位置移動到全關位置;后15 s 模擬發動機起動并逐漸加速到設計狀態,活塞桿從全關位置移動至全開位置,氣動載荷從0 逐漸增加到最大值。驅動函數曲線如圖3所示。IGV葉片的氣動扭矩曲線如圖4所示,前5 s氣動扭矩為0,后15 s逐漸從0增加到最大值。轉子葉片受到的軸向力和切向力隨時間的變化規律也一樣,前5 s時力為0,后15 s從0逐漸增大到最大值。轉子葉片VSV調節機構虛擬樣機模型最終效果如圖5所示。
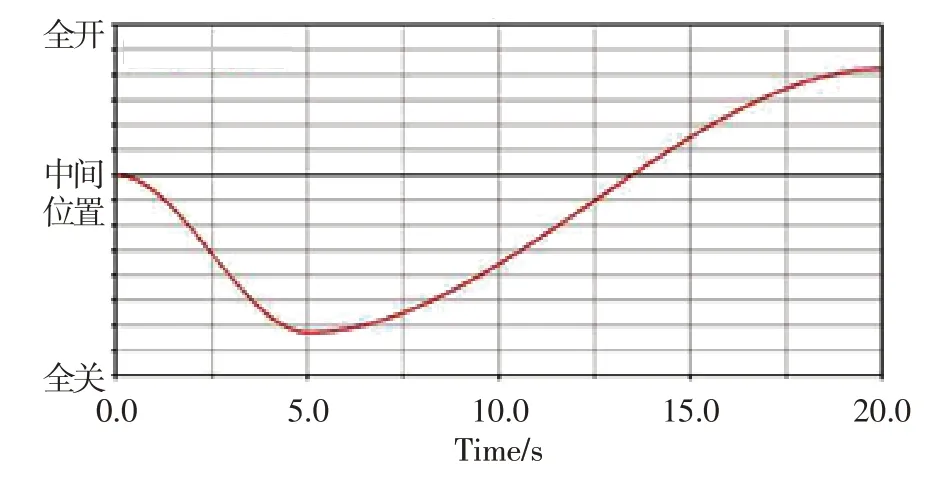
圖3 活塞桿行程曲線Fig.3 Stroke curve of piston rod

圖4 IGV氣動扭矩行程曲線Fig.4 Aerodynamic torque stroke curve of IGV vane

圖5 VSV虛擬樣機模型Fig.5 VSV virtual prototype model
2.4 聯動環柔性體轉化
完成VSV調節機構剛體模型建模以后,將各級聯動環轉化為柔性體。ADAMS 中采用模態綜合法將剛體轉化為柔性體。模態綜合法是將一個復雜結構分解成若干個較為簡單的子結構,在清楚掌握各子結構振動特性的基礎上,根據對接面上的協調條件將這些子結構合成一總體結構,然后利用各子結構的振動形態得出總體結構的振動形態。圖6示出了轉化為柔性體后的聯動環。

圖6 轉化為柔性體的各級聯動環Fig.6 Linkage rings converted to flexible bodies
3 仿真分析
3.1 剛體模型仿真分析
在開展VSV調節機構剛柔混合仿真之前,先進行了多剛體動力學仿真。圖7示出了進口導流葉片和可調靜子葉片調節角度隨時間的變化規律。可看出,同級不同角向位置角度曲線基本重合,不存在角度一致性問題。

圖7 葉片調節角度隨時間的變化規律Fig.7 The variation of the angles of the adjustable vane at each stage with time
以IGV 級葉片角度為基準,取每級葉片調節角度的平均值。將IGV級葉片調節角度平均值作為基準,查看S1葉片和S2葉片調節角度的平均值,并與設計值進行對比。為研究VSV 調節機構剛體模型的精度,計算了S1葉片和S2葉片的絕對誤差和相對誤差,結果見表2。表中的相對誤差等于絕對誤差除以該級靜子葉片的可調角度范圍。分析表2 可知,S1葉片和S2葉片調節角度的絕對誤差的絕對值均在0.1°以內,誤差較小。

表2 剛體模型中S1和S2葉片調節角度誤差Table 2 Errors of S1 and S2 in rigid body models
3.2 剛柔混合模型仿真分析
VSV調節機構中,聯動環的半徑最大,非常容易發生變形,從而對VSV調節機構的調節精度造成很大影響。為此,把各級聯動環轉化為柔性體,探究聯動環柔性對各級可調靜子葉片調節精度的影響。剛體模型中,每級聯動環支架數目均為6個,每級聯動環支架與機匣間的間隙均為0.20 mm。為研究聯動環支架與機匣之間徑向間隙以及支架數量對調節精度的影響,改變聯動環支架與機匣間的徑向間隙和周向分布數量,對比分析不同情況下的調節精度和調節角度一致性,最終得出一組合理的聯動環支架結構方案。本節用各級可調靜子葉片全開位置角度的最大絕對誤差反映調節角度精度,用各級可調靜子葉片調節角度標準差反映調節角度的一致性。
3.2.1 聯動環支架與機匣間徑向間隙對調節精度的影響
保持聯動環支架數量不變,改變聯動環支架與機匣間的徑向間隙,分別得出不同徑向間隙下的仿真結果,見表3。由表可知,隨著間隙增大,各級可調靜子葉片調節角度標準差的最大值也不斷增大。顯然隨著間隙增大,各級可調靜子調節角度一致性變差。
圖8采用折線圖方式直觀地表示了不同徑向間隙下的仿真結果。可看出,各級可調靜子葉片中,IGV的全開位置角度最大絕對誤差和調節角度標準差的最大值最小,S2的最大。分析VSV調節機構原理和誤差來源,其原因是:本文使用的調節機構屬于多級聯調機構,液壓作動筒通過搖臂和驅動臂直接帶動零級曲柄和零級聯動環運動,零級曲柄離原動件活塞作動筒距離最近,中間傳動部件少,累積誤差最小;零級曲柄通過零二連動桿帶動二級曲柄和二級聯動環轉動,而零二連動桿長度比零一連動桿約長一倍,同等截面和材料條件下結構穩定性較差,再加上各個運動副間隙誤差帶來的影響,使得S2的調節精度和調節角度一致性最差。根據表3和圖8可得出,當聯動環支架與機匣間的徑向間隙小于0.05 mm時,各級可調靜子葉片的調節精度和調節角度一致性變化較小,如S2 全開位置最大絕對誤差均小于1.4°,調節角度標準差的最大值均在0.5°以下,調節精度改善有限。徑向間隙在0.10~0.40 mm 時,各級可調靜子葉片的調節精度和調節角度一致性都隨徑向間隙的增加而變差。仍以S2為例,全開位置最大絕對誤差從1.227 074°增加到2.182 901°,增大了1.78倍;標準差最大值從0.391 369°增加到0.718 952°,增大了1.84 倍。當徑向間隙超過0.40 mm 后,除S2的調節精度和調節角度一致性隨徑向間隙的增大不斷變差外,其余兩級可調靜子葉片的變化不大,趨于穩定。據此,各級可調靜葉的調節精度和調節角度一致性跟聯動環支架與機匣間的徑向間隙呈負相關關系。綜合考慮調節精度要求和機匣工作時的受熱膨脹變形,各級聯動環支架和機匣間的徑向間隙應控制在0.05~0.10 mm之間。

表3 聯動環支架在不同徑向間隙下的仿真結果Table 3 Simulation results of different radial clearances of the linkage ring bracket

圖8 調節精度和一致性與徑向間隙的關系Fig.8 Adjustment accuracy and consistency in relation to radial clearance
3.2.2 聯動環支架周向分布數量對調節精度的影響
保持聯動環支架與機匣間的間隙為0.20 mm,改變聯動環支架周向分布數量,分別得出不同周向分布數量下的仿真結果,見表4。
不同聯動環支架周向分布數量下調節精度和一致性的仿真結果見圖9。由圖可知,在三級可調靜子葉片中,IGV的調節精度和調節角度一致性最好,S2 的最差。當支架少于4 個時,各級可調靜子葉片的調節精度和調節角度一致性趨于穩定,無大幅度變化。支架從4個增加到8個過程中,各級可調靜子葉片的調節精度和調節角度一致性隨聯動環支架數量的增加而變好。以S2為例,全開位置絕對誤差最大值從3.761 989°減小到0.872 764°,降低了76.8%;標準差的最大值從1.299 180°減小到0.299 600°,降低了76.9%。當支架超過8個后,各級可調靜子葉片的調節精度和調節角度一致性變化幅度不大,趨于穩定。據此,各級可調靜子葉片的調節精度和調節角度一致性與聯動環支架數量呈正相關關系。綜合考慮結構復雜程度和成本因素,建議聯動環支架周向分布數量為8個。

表4 不同聯動環支架數量下的仿真結果Table 4 Simulation results with different number of linkage ring brackets

圖9 調節精度和一致性與聯動環支架周向分布數量的關系Fig.9 Adjustment accuracy and consistency in relation to the number of linkage ring brackets
4 結論
以高壓壓氣機調節機構為研究對象,計算了剛體模型的調節精度,驗證了設計的合理性。通過改變聯動環支架與機匣間的徑向間隙及支架周向分布數量,探究了二者對調節精度和調節角度一致性的影響。主要得出以下結論:
(1) 在VSV 系統剛體模型中,各級可調靜子葉片的調節精度和調節角度一致性非常高,符合設計要求。
(2) 在VSV 剛柔混合模型中,各級可調靜子葉片的調節精度和調節角度一致性均比VSV 系統剛體模型的差。
(3) 聯動環支架與機匣間的徑向間隙對各級可調靜子葉片的調節精度和調節角度一致性有很大影響。徑向間隙越小,各級可調靜子葉片的調節精度和調節角度一致性越好。綜合考慮機匣的受熱膨脹,建議聯動環支架與機匣間的徑向間隙在0.05~0.10 mm范圍。
(4) 聯動環支架周向分布數量對各級可調靜子葉片的調節精度和調節角度一致性有很大影響。支架數量越多,各級可調靜子葉片的調節精度和調節一致性越好;但當支架數量超過8個后,調節精度和調節角度一致性改善并不明顯。建議聯動環支架周向分布數量為8個。

