一種基于平衡零差探測技術的平均光子數測量方法*

劉金璐 楊杰 張濤 樊礬 黃偉 徐兵杰

(西南通信研究所，保密通信重點實驗室，成都 610041)

針對連續變量量子密鑰分發系統實用化進程中對系統核心參數的規范標定需求，本文提出了一種基于平衡零差探測技術的平均光子數測量方法，即利用平衡零差探測基本結構，在本振臂添加一個電光相位調制器.不同于通過計算相位漂移值進行被動相位補償的方式，本方法主動地對相位調制器加載 [0，2π] 的均勻隨機相位以避免相位漂移對測量結果的影響.仿真及實驗驗證了平衡零差探測器輸出信號服從帶有兩個峰值的駝峰分布，且探測輸出信號方差與待測光脈沖平均光子數呈線性關系.采用該方案實現的平均光子數測量精度為0.1 個光子/脈沖，測量范圍達23 dB.優化選擇探測器性能和數據采集工具的采樣精度和量程，可實現滿足測量要求的平均光子數和脈沖消光比測量，為連續變量量子密鑰分發系統的關鍵參數標準化提供了一種可行方案.

1 引言

作為一種基于量子物理特性可為分離且合法的雙方提供共享密鑰的量子信息技術實用化手段，量子密鑰分發(quantum key distribution，QKD)被認為是可抵御量子計算機帶來的安全威脅的熱點研究方向.根據編碼過程的不同可將QKD 分為兩類:離散變量量子密鑰分發系統(discrete-variable quantum key distribution，DV-QKD)和連續變量量子密鑰分發系統(continuous-variable quantum key distribution，CV-QKD).相較基于BB84協議的DV-QKD 系統，基于高斯調制相干態協議(Gaussian-modulated coherent-state，GMCS)的CV-QKD 系統主要有以下4 點優勢:1)相干態光源較單光子源更易制備;2)編碼的量子態是準連續的，在希爾伯特空間具有無限維，使其在相對較短的距離具有潛在的高安全碼率特點[1-4];3)零差探測器較單光子探測器探測效率更高，成本更低;4)采用具有天然濾波特性的相干探測方法，表現出與現有光通信系統共纖同傳的潛力[5，6].目前國內外團隊在CV-QKD 與經典光信號共纖同傳方面開展了相關研究，并取得了一定的成果[7-9].2019 年，日本情報通信機構已實現CV-QKD 與100 個經典通信信道通過波分復用結構在10 km 光纖中共纖同傳[5]，系統實用化研究進展迅速.

在CV-QKD 系統實用化進程快速推進階段，系統關鍵參數的規范標定、擴展應用場景下的系統優化以及整體系統性能提升等方面的工作都亟待開展.相干態協議(含離散調制、高斯調制等)CV-QKD 系統是目前的主流研究方案，特別是基于隨路本振相干態協議的CV-QKD 系統已經得到了廣泛且深入的研究[1，2，7，8，10-13].系統中對發送端制備的本振光消光比要求極高，通常高達60—80 dB才能不在接收端引入泄漏光噪聲[14-17]，然而對于本振光的消光比指標的標定方法卻鮮有報道.對光子數差異達60—80 dB 的信號在同一標定方法下實現準確標定是很困難的，標定光子數常用的單光子探測器在測量“消光部分”的光子數時，較難避免由于來自“強光”部分的干擾造成的測量誤差.

本文提出了一種適用于CV-QKD 系統的平均光子數測量方法，利用平衡零差探測技術，結合相位隨機化的本振光脈沖，將對待測弱相干態脈沖信號的平均光子數的測量轉換為對零差探測輸出信號的數據方差統計.仿真和實驗表明，該方法具備一定條件下的本振光脈沖消光比測試能力，為CVQKD 系統的核心參數規范化測試提供了重要參考.

2 平衡零差探測模型及仿真分析

2.1 平衡零差探測器模型

常用的平衡零差探測(balanced homodyne detector，BHD)通常由1 個2 × 2 光分束器(beam splitter，BS)和1 個帶有2 個PIN 光電二極管的高增益低噪聲差分放大電路構成[18].將2 × 2 BS的2 個輸入臂依據輸入信號強度的不同分別命名為本振臂和信號臂，而兩個輸出臂信號分別進行強度和延時平衡后輸入進兩個響應度一致的PIN 管，對PIN 管輸出信號進行差分放大后，由模擬數字轉換器(analog-to-digital converter，ADC)對輸出電信號進行采集.當測試真空態的隨機漲落時，將信號臂斷開，調整輸入進本振臂的本振光強度即可獲取基于真空態隨機漲落的量子隨機信號[18-21]，采集獲得的信號統計方差稱為散粒噪聲方差.要利用這個模型進行平均光子數的測量，傳統方法是將待測信號接入信號臂，并在本振臂插入一個電光調制器.電光調制器的作用是對待測信號和本振光信號干涉中無法避免的相位漂移進行補償[21].然而這種依據零差探測結果計算相位漂移值并對電光調制器加載實時補償電壓的方式在高重復頻率的系統中實現起來是非常困難的.

理想零差探測器輸出的信號Xout可以表示為[22]

其中A為放大系數，XLO為本振光的x正則分量，和分別為信號光的x正則分量和p正則分量，θ為本振光和信號光之間的相位差.考慮到散粒噪聲波動及分布特性，和在測量時均呈現高斯分布，其均值分別代表在x分量和p分量上的振幅，兩個振幅的平方和即為該相干態的信號強度或平均光子數.

2.2 仿真分析

由于弱相干態脈沖信號在相空間上可以看成是由真空態(x和p分量均值為0，方差為v)進行平移后得到的，因此仿真時，和由兩組獨立同分布的高斯隨機數G1 和G2 來表征，均值分別為m1和m2，方差同為v，而σ2是該相干態脈沖信號的強度，與平均光子數正相關.在待測相干態信號的平均光子數一定的條件下，給本振光加載 [0，2π] 的隨機相位可使信號光與本振光的相位差θ也服從 [0，2π] 的均勻分布.由(1)式可知，采用主動控制信號光和本振光相位差的方法測量到的結果是同時包含了信號光的x分量和p分量的數據信息.在仿真中，令A和XLO均為1，樣本點個數為 107，結果如圖1 所示，探測結果分布呈現駝峰型.仿真獲得的探測輸出信號方差vout與相干態脈沖信號強度σ2的關系，結果如圖2 所示.可以看出，隨著σ2的增大，vout線性增大.由于σ2正比于平均光子數，換算關系可表示為

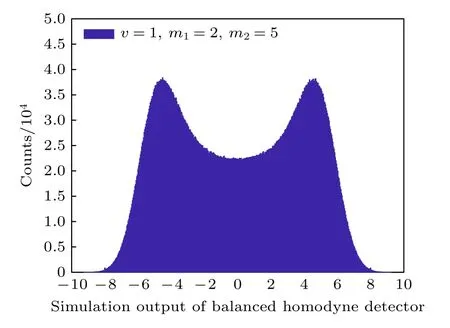
圖1 零差探測器輸出信號分布仿真結果Fig.1.Simulation distribution of BHD output.

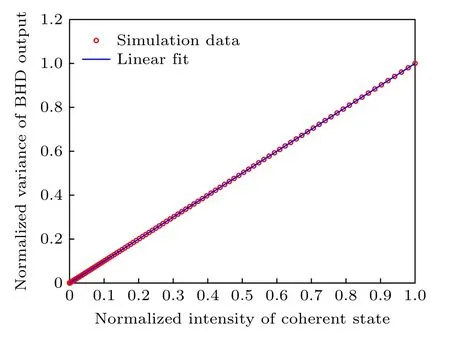
圖2 探測器輸出信號方差隨待測相干態信號的強度變化的仿真結果Fig.2.Variance of BHD output changes with the intensity of coherent state.

其中N為平均光子數;T為光脈沖重復頻率;λ為中心波長;h6.626×10-34J·s為普朗克常數;c3×108m/s為光速;P為平均光功率，其正比于σ2.由此可知，探測輸出信號方差vout與相干態脈沖信號的平均光子數N呈線性關系.

3 實驗方案及測量結果

依據設計方案搭建的實驗光路如圖3 所示.一束脈沖光經BS1 分束后，分為強度不同的上下兩支路，分別用來傳輸信號光和本振光.信號光通過一個光衰減器(VATT)后再由BS2 分成兩束，一束由光功率計(power meter)進行功率監測以計算平均光子數，另一束經強固定衰減器(CATT)后進入2 × 2 BS 的信號臂，作為待測平均光子數的相干態信號.本振光通過一個相位調制器(PM)并被加載 [0，2π] 的均勻分布隨機相位后輸入進2 × 2 BS 的本振臂，作為本振光信號，實現零差探測，并由ADC 最終完成數據提取.

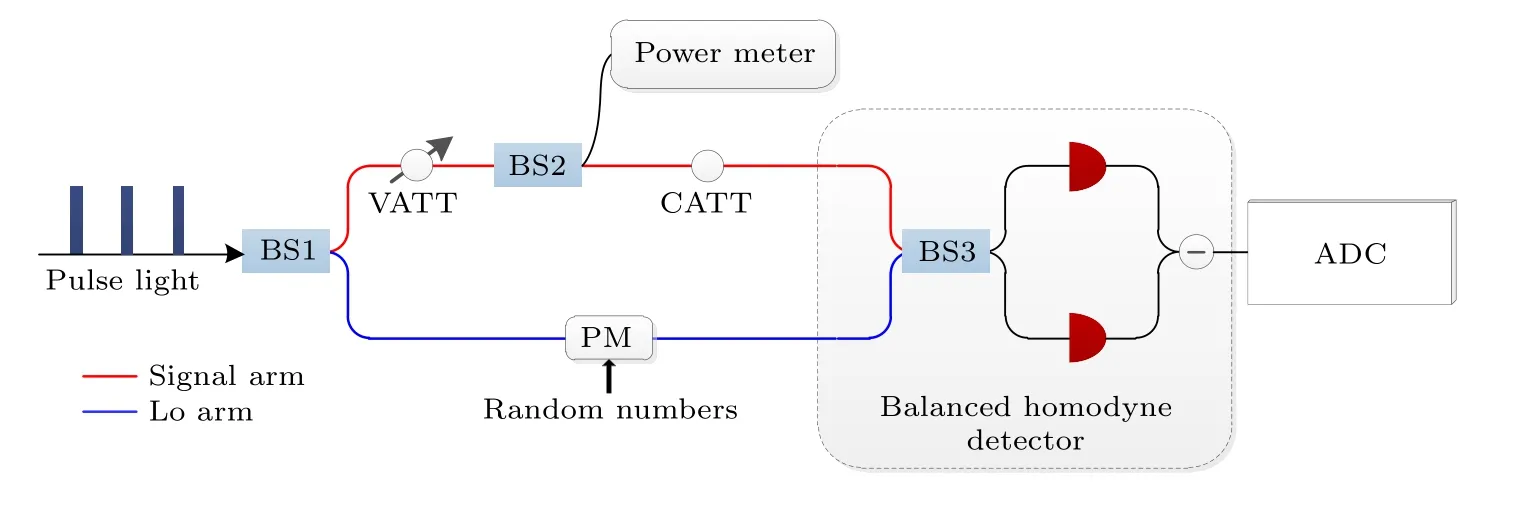
圖3 實驗裝置圖 (BS，光分束器;VATT，可調光衰減器;CATT，固定衰減器;PM，相位調制器;ADC，模數轉換器)Fig.3.Experimental setup.BS，beam splitter;VATT，variable attenuator;CATT，constant attenuator;PM，phase modulator;ADC，analog to digital converter.

實驗中的VATT 可控制弱光脈沖的強度，CATT 固定衰減值為—50 dB，以使進入探測器的信號為弱相干態脈沖信號.光脈沖重復頻率為1 MHz，寬度為30 ns (廠商:OPEAK，型號:LSM-DFB-100K-PL，其靜態線寬為100 kHz).由量子隨機數發生器[23]產生隨機數并加載在調制器PM (廠商:中國電子科技集團公司第四十四研究所，型號:GC 15PMTC7813，半波電壓Vπ3.5 V)上.由BS1和BS3 構成的等臂Mach-Zehnder 干涉儀的上下支路光纖長度均為4.52 m.對探測器輸出信號的峰值進行采樣[10]，采樣率為1 GSa/s，樣本量為 107.基于以上標定的零差探測器電噪聲為Vele0.07N0(N0為表征真空漲落的散粒噪聲方差).采集獲得的探測器輸出信號統計分布如圖4 所示，與仿真結果一致，呈現駝峰型.

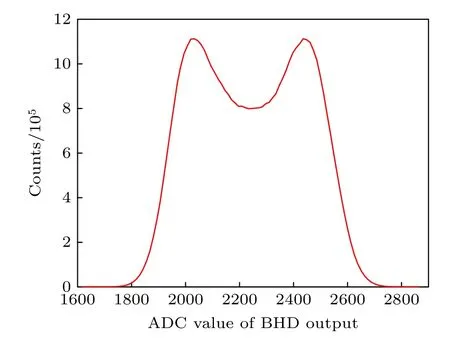
圖4 平衡探測器輸出信號分布Fig.4.Distribution of balanced homodyne detector output.

值得注意的是，仿真結果的兩個駝峰距離較實驗結果更遠，這是由于仿真采用的m1，m2和v與實驗中的待測信號光的平均光子數N和散粒噪聲N0存在差異.N越多或N0越小，兩個駝峰分離得越明顯，零差探測輸出信號方差越大.為此，對不同平均光子數的相干態脈沖信號進行測試，獲得的探測器輸出信號方差與平均光子數的關系如圖5所示，與仿真結果相符，探測器輸出信號方差與待測弱相干態信號的平均光子數呈現良好的線性關系.

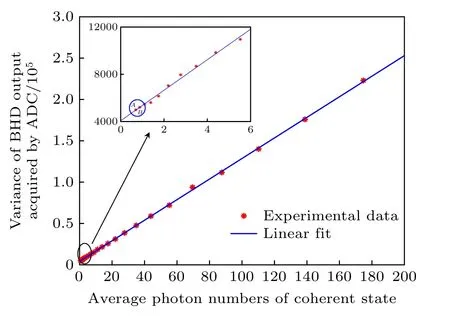
圖5 探測器輸出信號方差與平均光子數關系(電噪聲Vele=0.07N0，平衡零差探測效率 η=0.6044，ADC 采樣精度為14 bit)Fig.5.Variance of detector output varies with average photon numbers.Electrical nosie is Vele=0.07N0，the efficiency of BHD is η=0.6044 and sampling accuracy is 14 bit.

4 討論

在本方案中，本振光強度、零差探測器光電二極管探測效率、耦合器等無源光器件的透射率和ADC 采樣精度都會影響探測器輸出信號的方差值.而探測器輸出信號方差值所對應的平均光子數是依據光功率計測量值結合(2)式計算后得到的.因此，采用本方案進行實際應用時，應對探測器輸出信號方差值與平均光子數之間的一階線性關系進行校準，以保證本方案的實用性.

圖5 給出了平均光子數與零差探測器輸出信號方差之間的一階線性關系曲線，在實際實驗中是通過控制信號光支路的光功率以1 dB 步進變化，并計算對應平均光子數值，同時測量零差探測器輸出信號方差得到的.影響本方案量化精度的主要因素有:ADC 采樣精度和量程、光功率計測量不確定度以及探測器性能等.

其中ADC 是將探測器輸出的模擬電壓信號轉化成數字信號，其可分辨的最小模擬電壓由ADC采樣精度和量程決定，因而實驗獲得的探測器輸出信號方差值的最小可分辨值也是由ADC 決定的.在采樣精度、量化量程確定的情況下，輸出信號方差的最小可分辨值是確定的.實驗中使用的光功率計生產廠家為Thorlabs，型號為PM20CH，其測量不確定度為±0.25 dB (＜ 1 dB).光功率越小，依據其測量結果計算得到的平均光子數越準確.由于ADC 提取數據信號的最小可分辨方差值是確定的，因此在圖5 中實驗結果的典型值給出了探測輸出信號方差與平均光子數之間的趨勢關系，其測量精度是由ADC 能夠分辨的最小方差值來保證的.

圖5 所示的實驗結果中，藍色圓圈線中A和B兩個點縱坐標方差值分別為4990.8 和5200.1，對應平均光子數分別為0.696 個/脈沖和0.827 個/脈沖，差值為0.131 個/脈沖.因此，將實驗測得的最小可分辨方差值對應的可分辨平均光子數近似為0.1 個/脈沖作為本方案測量精度.

有關ADC 性能與本方案的量化精度之間的關系，以及測量結果的誤差來源分析是一個非常值得研究的問題，我們會在接下來的工作中在這個方向繼續深入.

由于采用了主動控制本振光相位并將其隨機化的方法，本方案同樣適用于光脈沖時域消光比的測量.即為信號光添加延時，按需要控制衰減器的衰減值并先后標定脈沖光“有光”和“無光”部分的光子數，而無需考慮由于激光器相位噪聲引入的測量誤差.

實驗表明，依據平衡探測的輸出方差來獲得當前光脈沖的平均光子數是切實可行的技術方案.

5 結論

本文提出了一種基于平衡零差探測技術測量光脈沖平均光子數的方法，采用對本振光相位隨機化消除相位漂移引入的測量誤差.仿真并實驗驗證了零差探測器輸出信號方差與光脈沖平均光子數的線性關系，采用該方案實現的平均光子數測量精度為0.1 個光子/脈沖，測量范圍達23 dB.為連續變量量子密鑰分發系統中平均光子數和光脈沖消光比的測量提供了一種參考方案.