基于異類類內超平面的模糊支持向量機及其應用

陳繼強，余志鵬，張 峰，張麗娜

(河北工程大學 數理科學與工程學院，河北 邯鄲 056038)

個人信用評估是指銀行等金融機構通過對影響借貸人還款的各種主客觀條件環境的綜合考察，運用嚴謹的科學方法評估借貸人的借貸信用及其還款能力，從而對借貸人是否具有履行償還銀行等金融機構的借貸能力進行評估，本質上是一個不平衡數據集的二分類問題。然而，我國的信征體系發展較晚，個人信用評估模型的研究尚不完善，亟需進行深入研究。

專家評分模型[1]是最早被應用于個人信用評估的模型，但是由于其評估結果易受主觀因素干擾等問題，逐漸被舍棄。后來，Carter& Catlett[2]將Fisher判別分析運用到個人信用評估領域，Orgler[3]利用線性回歸分析方法建立了個人信用評估模型，都取得了一定的成果。然而，這種基于統計學的方法難以處理信貸數據集中的噪聲數據。后來，隨著機器學習理論的發展，一些學者將決策樹與支持向量機等機器學習算法應用于信貸評估[4-12]，均取得較好的效果。但是，這類方法在處理不平衡信貸數據集時的分類能力是有限的。隨著科學技術水平的發展，一些學者致力于集成模型在個人信用評估領域中的應用研究。例如，丁嵐駱等[13]構建了Stacking集成策略的借貸人違約風險評估模型。夏國斌[14]將基于Bagging集成法的集成支持向量機模型運用于個人信用評估中，饒希[15]將基于Boosting集成法的邏輯回歸與支持向量的集成模型運用于個人信用評估中。郭孝敬[16]運用了基于邏輯回歸與決策樹的集成模型，王思懿[17]將隨機森林與邏輯回歸的集成模型運用到個人信用評估中，張碧月[18]實驗結果表明RF-APSOLSSVM的預測精度比RF模型和APSOLSSVM模型的精度高。王黎等[19]的實驗結果表明GBDT模型明顯優于支持向量機和邏輯回歸的效果。趙天傲等[20]將XGBoost算法應用在個人信用風評估中，與決策樹、支持向量機等模型進行對比分析，實證結果表明XGBoost模型比單一模型的預測精度提升效果比較明顯。雖然集成模型分類效果相對于其單一模型分類效果較好，但是它們同單一模型一樣也沒有考慮不平衡信貸數據集中噪聲數據對于分類結果的影響。

綜上所述，當前關于個人信用評估問題的研究，現有方法沒有很好地處理不平衡信貸數據集中噪聲對模型分類精度的影響。因此，為了降低噪聲數據對模型分類精度的影響，本文考慮了不同樣本在分類問題中的不同作用，構建了一種基于異類類內超平面的模糊支持向量機，為信貸評估問題提供了一種新方法。

1 支持向量機簡介

支持向量機是20世紀90年代中期由Cortes和Vapink提出的一種有監督的學習方法。其基本思想是通過最大化間隔尋找最優分類超平面，從而對數據進行分類，自提出以來被廣泛應用[21-23]。

為不失一般性，這里以二分類問題為例。假設給定的訓練集為

T={(x1,y1),…,(xn,yn)}

(1)

其中xi∈Rm,yi∈{-1,+1}為類標簽，i=1,2,…,n。對于非線性分類問題，通過映射φ(x),將訓練數據集從原空間映射到高維特征空間，使得映射后的數據集在特征空間中線性可分。因此，支持向量機的學習問題可用如下二次規劃問題來描述：

s.tyi(ω·φ(xi)+b)≥1-ξi

ξi≥0,i=1,2,…,n

(2)

其中‖·‖表示向量的模，C>0為懲罰參數，ξi為松弛變量。原問題(2)的求解可通過構造拉格朗日函數，轉化為如下對偶問題來求解：

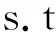
0≤αi≤C，i=1,2,…,n(3)

問題(3)中K(xi,xj)=(φ(xi),φ(xj))為核函數，αi為拉格朗日乘子。

通過求解對偶問題(3)可得分類函數為

進一步可得決策函數為

f(x)=sgn(g(x))

這樣，對于新的樣本x′,其預測類別為f(x′)。

2 基于異類類內超平面距離的隸屬函數

隸屬函數是模糊數學中的一個重要內容，可用于為不同樣本設定不同的權重[24-27]。本文考慮到在支持向量機中對確定最優分類超平面起決定性作用的只有支持向量，而支持向量的位置一般又位于距離異類點較近的區域。為此將模糊理論引入支持向量機中，設計了基于異類類內超平面距離的隸屬函數。該方法的思想是根據每個向量到異類類內超平面距離的不同，將樣本輸入xi到異類類內平面距離的函數作為隸屬函數，對訓練集中的輸入xi賦予相應的權重(隸屬度)來提高支持向量在訓練樣本中的作用。

如圖1所示，對于訓練樣本集{(x1,y1),(x2,y2),…,(xn,yn)},假設正類樣本(在圖中用菱形表示)數目為n1，負類樣本(在圖中用圓形表示)數目為n2,n1+n2=n。在線性不可分時，通過映射φ(x),將數據集從樣本空間映射到特征空間，數據集變為{(φ(x1),y1),(φ(x2),y2),…,(φ(xn),yn)}。

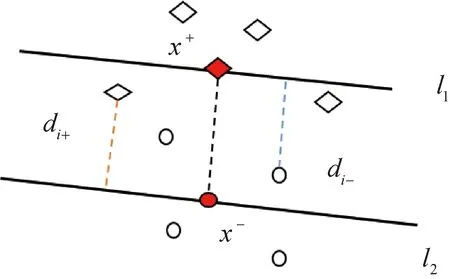
圖1 基于異類類內超平面的距離示意圖Fig.1 Diagram for the distance of heterogeneous hyperplane

因此，正類樣本點xi到負類類內超平面l2的距離可定義為

(4)

同理，負類樣本點xi到正類類內超平面l1的距離可定義為

(5)

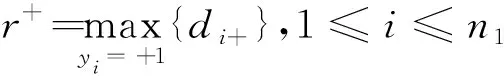
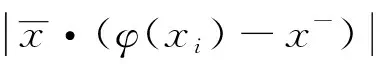
=|(x+-x-)·(φ(xi)-x-)|

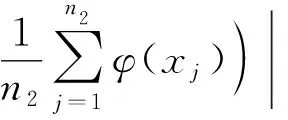
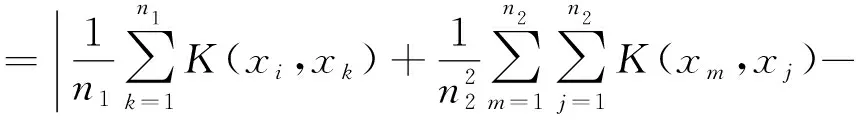
同理，當yi=-1時，di-的分子及r-可分別表示為

這樣，為了表示第i個樣本隸屬于對應類標簽的程度，可設計如下基于樣本點到異類類內超平面距離的隸屬函數

(6)

式(6)中σ是一個給定的很小的正數，目的是為了保證隸屬函數μi的取值大于0。

3 基于異類類內超平面的模糊支持向量機

傳統的支持向量機是把所有的訓練樣本看作同等重要的，這使得獲得的分類超平面對噪聲數據或者非支持向量樣本較為敏感，從而導致獲得的最優分類超平面存在偏差，進而影響分類器的分類精度。為了克服上述問題，本小節將上節設計的隸屬函數賦予每個向量不同的權重，并結合傳統支持向量機，構建基于異類類內超平面的模糊支持向量機。

在引入隸屬函數μi后，訓練樣本集{φ(xi),yi}變為{φ(xi),yi,μi}其中0≤ui≤1,i=1,2,…,n,它表示第i個樣本隸屬于對應類標簽的程度。這樣，可建立如下二次規劃問題：

s.tyi(ω·φ(xi)+b)≥1-ξi

ξi≥0,i=1,2,…,n

(7)

其中C>0為懲罰參數，μi為式(6)給出的隸屬函數，ξi為松弛變量。對于原問題(7)，通過構造拉格朗日函數，可轉化為如下對偶問題：

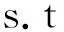
0≤αi≤μiC,i=1,2,…,n

(8)

其中K(xi,xj)=(φ(xi),φ(xj))為核函數，αi為拉格朗日乘子。結合傳統支持向量機，可設計求解上述優化問題的求解算法，該算法就稱為基于異類類內超平面的模糊支持向量機。

下面將通過UCI數據集和信用評估問題的實驗驗證所設計算法的有效性。

4 實驗

UCI數據庫是加州大學歐文分校(University of CaliforniaIrvine)開發的用于機器學習的數據庫，UCI數據集是眾多學者常用的標準測試數據集。為了驗證上述構建的基于異類類內超平面的模糊支持向量機的有效性，本節將首先利用UCI數據集選擇部分數據進行實驗，然后在個人信用評估問題中驗證該方法的有效性。

4.1 模型評估指標

考慮到數據集的不平衡性，選取F1值。F1是非平衡數據集分類問題中有效的評價準則之一[28]，它是基于混淆矩陣的一個評估指標，詳見式(9)。

在分類任務中，混淆矩陣是一個N×N的矩陣，其中N是被預測的類別數，在本文中由于是一個二分類任務，所以混淆矩陣是一個2×2的矩陣。表1是一個二分類任務中的混淆矩陣實例表。

表1 基于二分類的混淆矩陣

F1的計算表達式為[25]

(9)

4.2 基于UCI數據集的實驗

本小節選取UCI數據庫中4個不同的數據集進行實驗，各數據集的樣本數量、屬性數量、正負類樣本數量詳見表2。

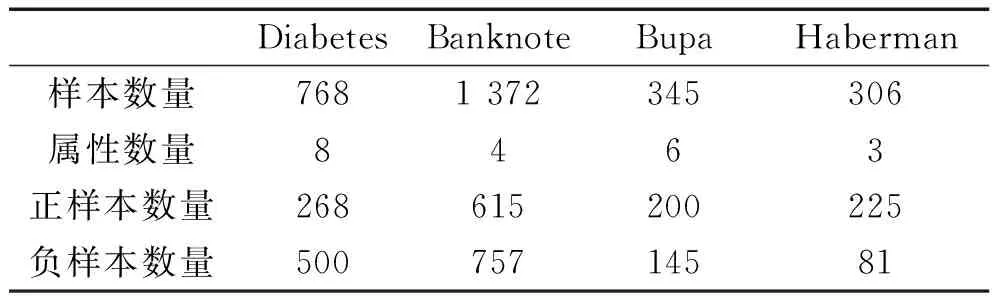
表2 數據集描述

為了驗證本文提出的基于異類超平面的模糊支持向量機(DHFSVM)的有效性，將它與傳統的支持向量機(SVM)、決策樹(DTC)、高斯樸素貝葉斯模型(GNB)三種模型分別在4種UCI數據集上進行實驗，實驗結果如圖2所示。

從圖2中可以看出，DHFSVM算法在Bupa、Diabetes、Habeman等3個數據集上的F1值為最高，在Banknote數據集上為第二高。這說明，本文所構建的DHFSVM算法考慮了不平衡數據集中不同樣本在分類過程中的不同作用，有效地提高了不平衡數據分類的準確性。

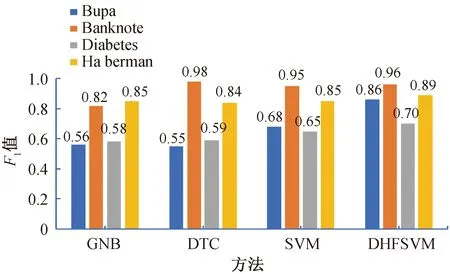
圖2 基于GNB、SVM、DTC與DHFSVM在數據集上的F1值柱狀圖Fig.2 Histogram of F1value with GNB,SVM,DTC and DHFSVM

4.3 個人信用評估中的應用

在個人信用評估問題中，信貸數據涉及到個人隱私等問題，眾多信貸數據無法開放獲取，因此本文中采用來自Kaggle數據科學競賽平臺上的信貸數據集，該數據集的名稱為“Give Me Some Credit”。在該數據集中，包含10個解釋變量xi,i=1,2,…,10,一個被解釋變量y。具體如表3所示。

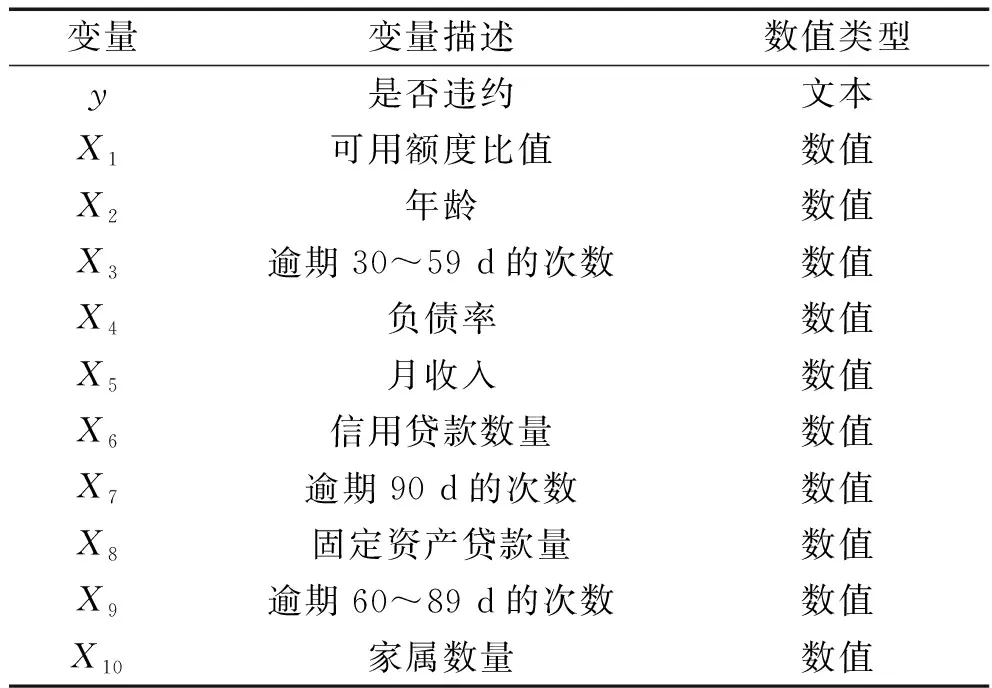
表3 變量及其描述

由于該數據集數量較大(將近15萬條)，本實驗隨機選取了其中的1 000條數據，其中違約數據為200條，未違約數據為800條。在圖3中，給出了GNB、SVM、DTC以及DHFSVM基于“Give Me Some Credit”數據集的分類混淆矩陣。

由式(9)F1值及如圖3所示的混淆矩陣可以計算得出各個模型對應的F1值，結果如圖4所示。

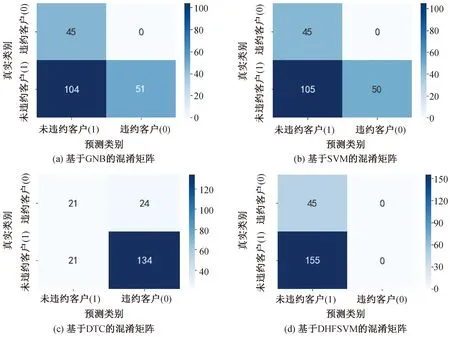
圖3 基于GNB、SVM、DTC和DHFSVM的混淆矩陣Fig.3 Confusion matrices with GNB,SVM,DTC and DHFSVM

由圖4所示的結果可以看出，在GNB、SVM、DTC和DHFSVM 4種算法中，本文所構建的DHFSVM算法表現最好，取得了最大的F1值0.87。這說明，在分類算法的構建時，充分考慮不平衡數據中不同樣本點(包含噪聲)所起的不同作用，可有效提高分類算法的精度，也說明了本文所構建的DHFSVM算法可以較好地應用于個人信用評估問題。

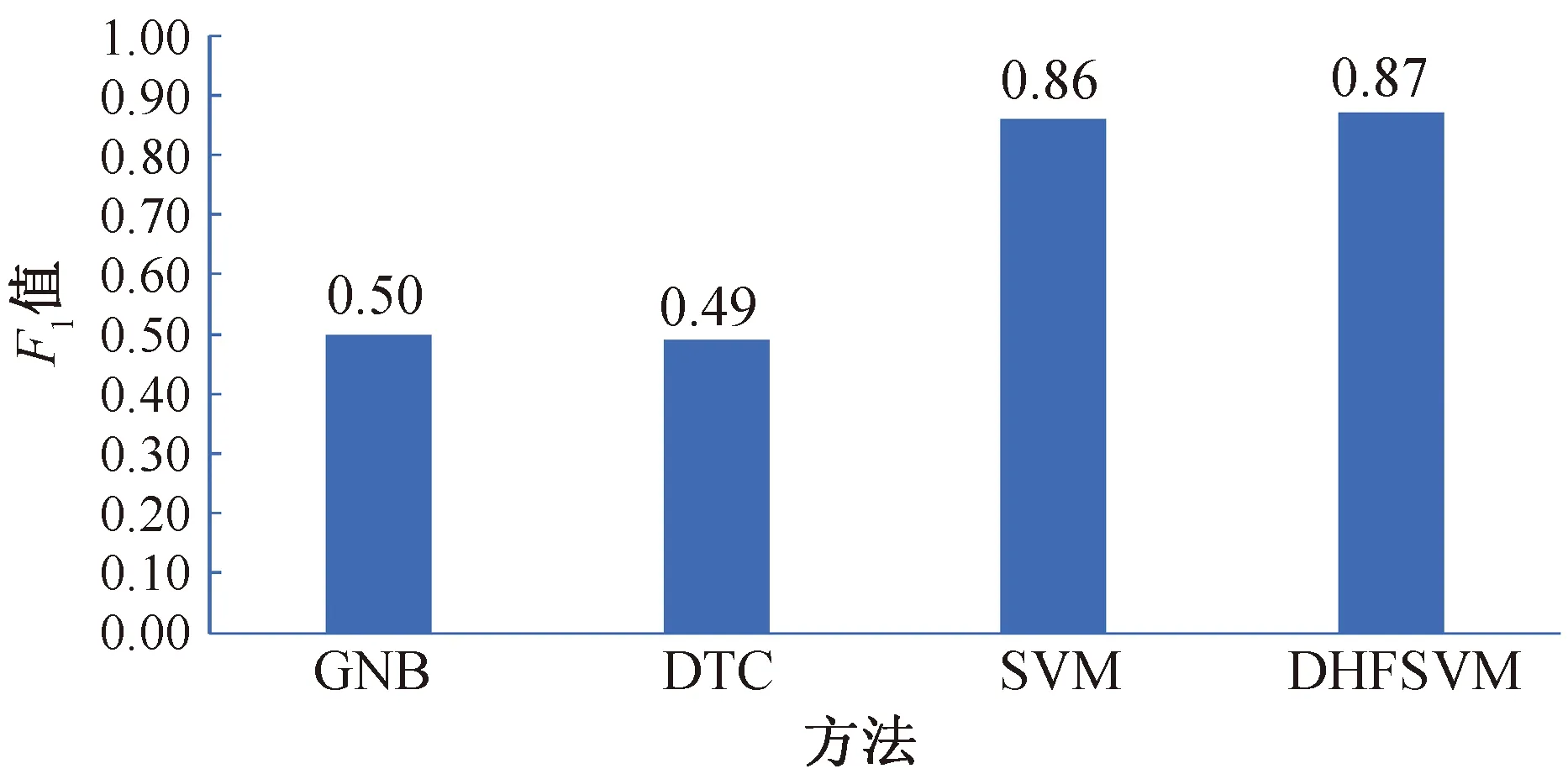
圖4 基于GNB、SVM、DTC與DHFSVM在信貸數據集上的F1值柱狀圖Fig.4 Histogram of F1 value on the credit data with GNB,SVM,DTC and DHFSVM

5 結論

本文結合模糊數學理論、經典支持向量機，構建了一種基于異類類內超平面的模糊支持向量機(DHFSVM)。與GNB、DTC、SVM 3種方法對比發現：(1)DHFSVM算法在Bupa、Diabetes、Habeman等3個數據集上的F1值最高，在Banknote數據集上第二高，表明所構建的DHFSVM算法可通過賦予不同樣本不同的權重來降低噪聲對風險評估帶來的影響；(2)在Kaggle數據科學競賽平臺上提供的真實信貸數據集進行的實驗發現，DHFSVM算法表現最好，取得了最大的F1值。表明DHFSVM算法可有效提高不平衡信貸數據集的分類準確性，可為個人貸款業務中個人信用風險評估問題提供借鑒。