直線與方程學習導航

■胡 彬

從近幾年的高考題來看,求直線方程、確定兩條直線的位置關系、距離公式的應用是高考的常考點。

一、基礎重現

1.直線的傾斜角與斜率

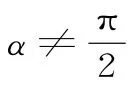
溫馨提醒：任意一條直線都有傾斜角,只有與x 軸不垂直的直線才有斜率。當傾斜角α=0時,k=0;當α 是銳角時,k>0;當α 是鈍角時,k<0。

2.直線方程

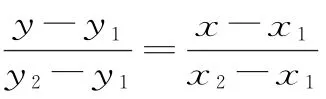
3.兩條直線的位置關系

(1)判斷兩直線平行的方法:判斷兩直線的斜率是否存在,若k1=k2且b1≠b2,則兩直線平行;若斜率都不存在,還要判斷是否重合。(2)判斷兩直線垂直的方法:判斷兩直線的斜率是否存在,若k1·k2=-1,則兩直線垂直;若一條直線的斜率不存在,另一條直線的斜率為0,則兩直線也垂直。

二、考點舉例

例1 直線l 經過點A(1,2),在x 軸上的截距的取值范圍是(-3,3),則其斜率的取值范圍是_____。

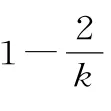
例2 過兩直線2x-y-5=0 和x+y+2=0的交點且與直線3x+y-1=0平行的直線方程為_____。

例3 求與直線2x-y-1=0平行,且與直線2x-y-1=0 的距離為2 的直線方程。