緯編針織機織針自由狀態下固有頻率測試方法

戴 寧， 彭來湖， 胡旭東， 崔 英， 鐘垚森， 王越峰

(浙江理工大學 浙江省現代紡織裝備技術重點實驗室， 浙江 杭州 310018)

織針作為緯編針織機重要的編織機構，其在退圈、集圈等高度位置的振動特性與緯編織物的品質密切相關，織針的振動主要來自織針與三角間的相互作用，當三角對織針的激勵達到織針固有頻率時，導致織針共振，將直接影響退圈、彎紗等工藝動作。近年來，針對織針與三角相關的研究也越來越多，浙江理工大學的張華[1]、武漢紡織大學張成俊[2]等對織針與三角間的相互作用進行了動力學建模并對織針與三角間的沖擊和碰撞通過相應的實驗進行了驗證，但二者對織針的研究主要還停留在剛體運動層面，并未從振動層面對改善織針振動進行研究，而織針自由狀態下固有頻率測試方法是分析織針振動特性的前提。織針細長、扁平的幾何特性可等效為兩端自由梁，目前，采用壓電陶瓷材料對梁固有頻率測試的研究較多，如劉永春[3]、唐治[4]等采用壓電陶瓷對懸臂梁固有頻率測量及抑振進行了相關研究，但其研究對象結構簡單、尺寸較大、且單端固定，而緯編針織機織針尺寸相對微小，對于其在自由狀態下固有頻率的有效測量具有一定難度。

本文借鑒壓電陶瓷測振原理并結合織針自身的結構特點，采用將小矩形PZT薄片貼敷于織針針桿表面，形成PZT、織針黏合體結構。通過阻抗分析儀WK6500B對黏合體進行掃頻激勵，獲取黏合體在寬頻范圍內復阻抗及相位角的響應特性，當掃頻頻率達到黏合體固有頻率時，黏合體復阻抗及相位角響應曲線出現突變。采用ANSYS有限元仿真軟件分析PZT薄片質量對織針固有頻率測量誤差的大小，并引入懸臂梁曲率理論，對PZT測振方法進行理論指導。本文提出的織針固有頻率的測試方法對織針振動理論的研究具有一定意義。

1 研究方法概述

織針是緯編針織機成圈編織機構中重要的編織執行器件，而成圈編織機構性能的優劣直接影響緯編織物的品質。織針沿三角表面做受迫升降運動，紗線在織針上下運動過程中，彎曲成線圈，根據新舊線圈和織針針舌的相對位置，成圈過程可分為起針、退圈、墊紗、閉口、套圈、脫圈、彎紗、成圈以及牽拉階段，新舊線圈相互串套形成織物[5-7]，緯編針織機編織過程織針運動簡圖如圖1所示。

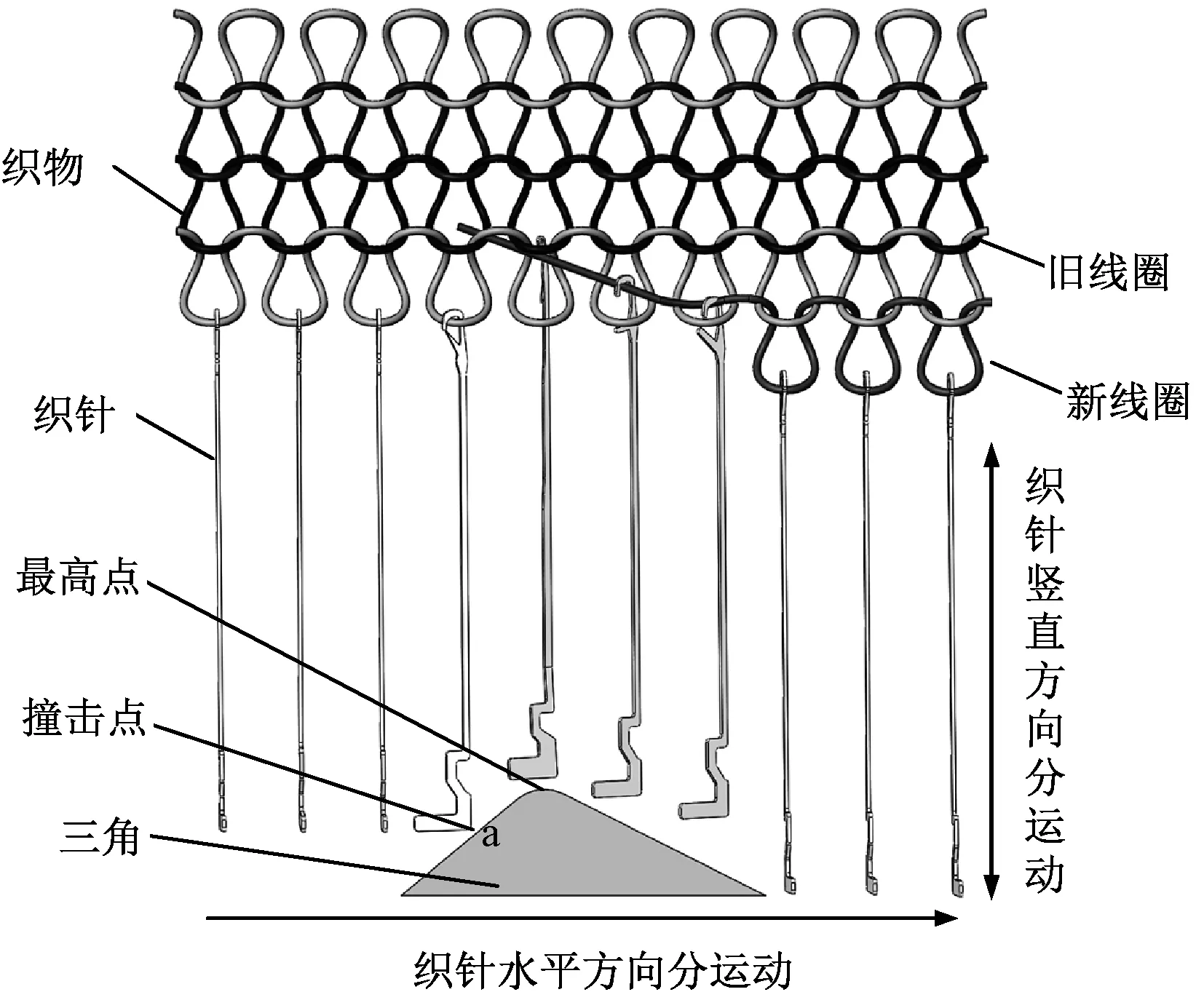
圖1 緯編針織機成圈過程織針運動簡圖Fig.1 Simplified diagram of knitting needle movement during loop forming process of weft knitting machine

由圖可知，織針隨針筒運轉，并與三角表面a點發生撞擊后沿三角表面運動，此瞬態撞擊過程將引起織針的振動，并且由于織針沿三角表面做受迫運動，三角本身的機械振動也會引起織針的隨機振動[8-10]。當織針發生振動時，成圈過程中織針針舌豎直高度與新舊線圈的相對位置發生變化，直接影響織物的成圈效果，形成疵點。研究緯編針織機織針的振動特性對提高其性能的穩定性至關重要，而織針自由狀態下的固有頻率特性的測量是研究針織振動特性的前提。本文結合織針尺寸及外形特性，應用共振理論，設計了織針固有頻率測試方式，并采用ANSYS有限元仿真軟件進行分析，對織針固有頻率測試方案進行驗證，本文總體設計方法如圖2所示。

圖2 織針固有頻率總體設計方案簡圖Fig.2 Schematic diagram of overall design of the natural frequency of the knitting needle

圖2示出織針固有頻率總體設計簡圖，本方案采用將小尺寸PZT薄片粘貼于織針針桿表面形成織針、PZT黏合體，并采用阻抗分析儀內部控制模塊設置掃頻范圍以及掃頻信號電壓幅值參數，內部驅動模塊對掃頻信號進行放大后加載于黏合體上，當掃頻頻率到達黏合體固有頻率時，引起黏合體共振，導致黏合體阻抗畸變，PZT壓電效應增強，阻抗分析儀對掃頻范圍內黏合體的阻抗特性變化信號進行處理，產生掃頻范圍內黏合體的復阻抗以及角度數據，并采用MatLab處理，形成復阻抗-頻率，相位角-頻率曲線。為了檢測測試數據的準確性，采用SolidWorks軟件建立織針三維模型，并采用ANSYS軟件進行有限元處理，通過對比分析驗證測試方案的準確性。

2 實驗方法

本文采用阻抗分析儀測試黏合體的固有頻率來近似確定織針的固有頻率，PZT的額外引入將改變織針原有結構的質量與剛度，故實驗要求PZT的質量小，貼敷面積小，貼敷厚度薄，貼敷層無雜質等要求。黏合體剖面結構圖如圖3所示。

圖3 黏合體剖面結構圖Fig.3 Cross-section structure of bonded body

采用英國穩科公司(Wayne Kerr)型號為WK6500B的阻抗分析儀對黏合體結構進行阻抗分析，將黏合體上的2條細直導線接入WK6500B阻抗分析儀，實驗連接圖如圖4所示。

圖4 實驗連接圖Fig.4 Diagram of experimental connection

當對黏合體表面施加交流電場時，由于逆壓電效應，PZT產生與交流電場同頻率的機械振動，此時與PZT黏合在一起的織針對PZT機械振動產生振動響應，并反作用于PZT。PZT由于正壓電效應，使得PZT表面電信號發生變化，并等效為PZT電阻抗發生變化。當交流電頻率達到織針固有頻率時，織針振動幅度畸變引起PZT電阻抗發生突變，即黏合體復阻抗發生突變。對阻抗分析儀設置合適的掃頻范圍，進行阻抗分析，引起黏合體復阻抗突變點對應的頻率即為黏合體的固有頻率，當PZT的質量足夠小時，可用黏合體的固有頻率近似表示針織的固有頻率。阻抗分析儀測量黏合體固有頻率原理如圖5表示。

圖5 阻抗分析儀測量黏合體固有頻率原理Fig.5 Principle of measuring natural frequency of bonded body by impedance analyzer

如圖5所示，PZT無間隙粘貼于織針表面形成黏合體，黏合體的機電耦合特性用PZT的機械阻抗Zp代替，其值大小為阻抗分析儀輸出的電壓V與流入阻抗分析儀的電流I的比值。織針機械阻抗Zn的大小為PZT激振力與織針振動響應速度的比值。黏合體的復阻抗表達式如式(1)所示。

(1)

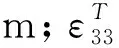
由式(1)可知，PZT與織針的結構特征及PZT的壓電特性保持不變，故黏合體的復阻抗與阻抗分析儀交流激勵電壓的頻率有關，當其達到黏合體固有頻率時，PZT的機械阻抗Zp發生突變，由公式(1)可得，此時黏合體復阻抗發生突變。故采用阻抗分析儀可正確測量黏合體的固有頻率。

設置合適的掃頻頻率范圍以及電壓幅值，對黏合體進行阻抗分析，采用MatLab繪制復阻抗-頻率，角度-頻率曲線并進行分析，如圖6所示。

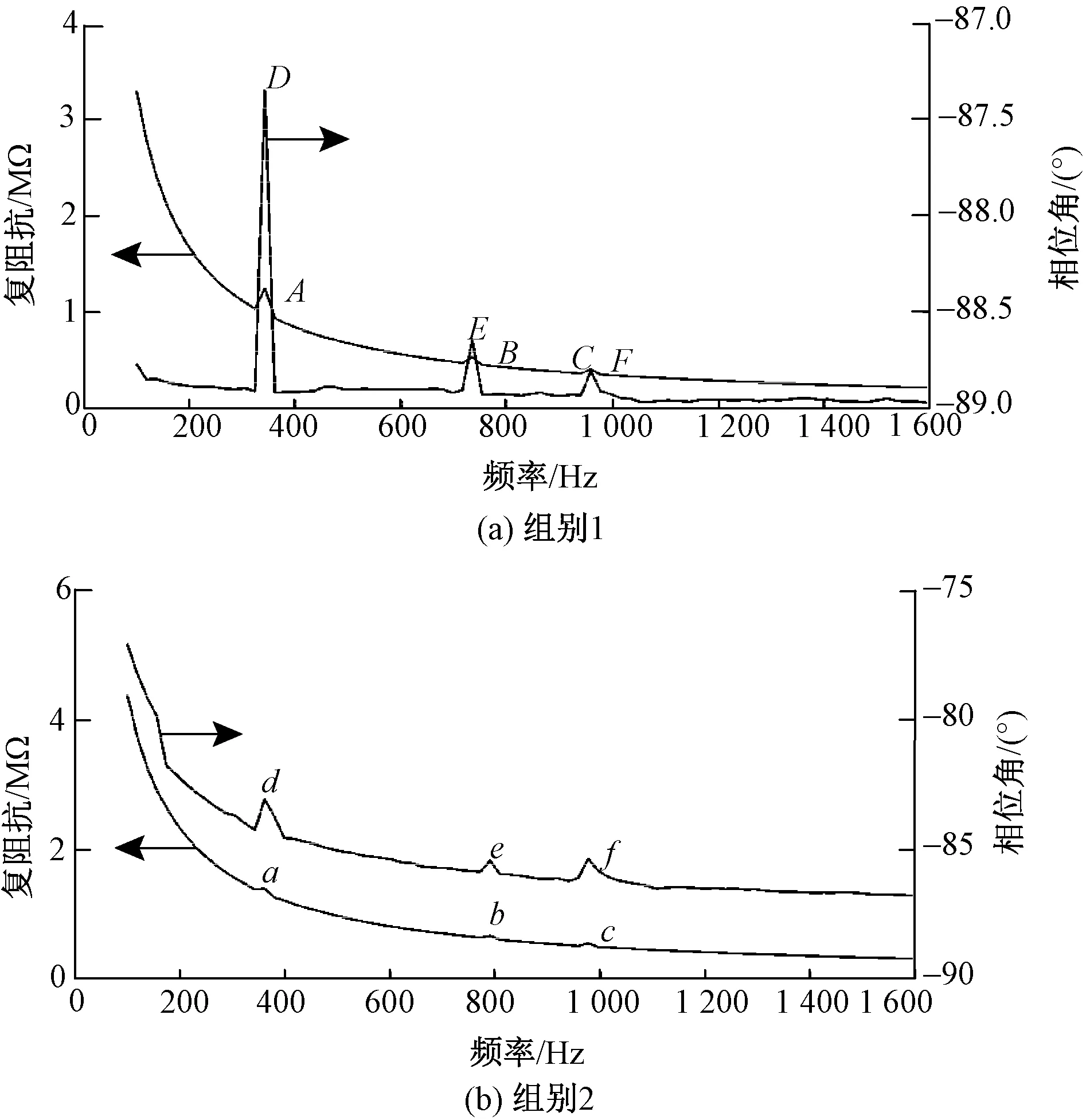
圖6 復阻抗-頻率與角度-頻率曲線圖Fig.6 Graph of complex impedance-frequency and angle-frequency. (a) Group 1; (b) Group 2

圖6示出2組實驗中黏合體的復阻抗-頻率與相位角-頻率曲線。圖6(a)中A、B、C點為復阻抗曲線中3個尖峰點，其橫坐標代表的頻率值分別為342.4、734.0、957.8 Hz，D、E、F點為相位角曲線中3個尖峰點，其橫坐標代表的頻率值分別與A、B、C3點的橫坐標值相等。圖6(b)中a、b、c點為復阻抗曲線中3個尖峰點，其橫坐標代表的頻率值分別為361.1、790.0、976.5 Hz，d、e、f點為相位角曲線中3個尖峰點，其橫坐標代表的頻率值分別與a、b、c3點的橫坐標值相等。單獨分析其中任意一組實驗可知，不同頻率下的復阻抗以及相位角“尖峰值”存在差別，其值的大小反應了PZT壓電特性的強弱程度。織針在不同模態下，同一位置的形變程度存在差異，具體體現在織針形變彎曲下的曲率存在差別，如圖7所示。PZT貼于織針表面，PZT壓電特性的強弱與織針表面彎曲時曲率值相關。

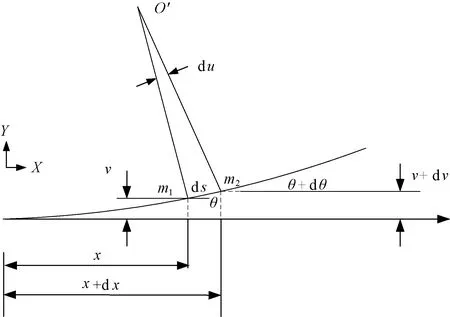
圖7 彎曲時織針表面曲率示意圖Fig.7 Schematic diagram of surface curvature of knitting needles during bending

圖7示出織針表面的曲率示意圖，O′表示曲率中心，點m1、點m2為位于織針彎曲面上2點。x、x+dx分別為點m1、點m2的橫向位置，單位為m；θ、θ+dθ分別為點m1、點m2的旋轉角度，單位為rad；v、v+dv分別為點m1、點m2的撓度，單位為m；ds為點m1、點m2間的弧長，單位為m。故可得曲率：

(2)

各階模態響應下，織針同一位置處曲率K的大小存在差別，故貼于織針特定位置處的PZT在織針各階模態響應時表現的壓電特性存在差距。從而導致同一組試樣下阻抗分析儀中不同頻率下的復阻抗以及相位角存在差別。

對比試樣1、試樣2中各階模態下的頻率，并繪制表格，詳細如表1所示。

表1 試樣1,2前3階頻率統計表Tab.1 Statistical table of the first three order frequency of sample 1 and 2 Hz

對比表1中試樣1、2可知，兩組實驗的黏合體為人工操作，故PZT的尺寸，織針與PZT黏合層的實際接觸面積、厚度，黏合層內部的雜質濃度，織針與粘貼層的相對位置等均存在差異，進而導致兩組實驗的復阻抗、角度曲線以及各階模態下的頻率存在細微偏差。

3 ANSYS有限元仿真分析

采用ANSYS有限元仿真軟件分析時，仿真對象的幾何結構建模可以通過其內置的Design Modeler模塊進行繪制，但用該模塊繪制織針結構模型較為煩瑣，故本文首先在SolidWorks軟件中創建織針的三維幾何模型，并將其轉化為igs文件后導入ANSYS仿真軟件中。完成導入后，在ANSYS仿真軟件中對織針的材料屬性進行設置，織針的材料為結構鋼，定義彈性模量為2×1011Pa、泊松比為0.25、密度為7 850 kg/m3。材料屬性定義設置后，完成織針的網格劃分，并不設置織針任何約束條件，使織針處于完全自由狀態下。在完成所有設置后，采用ANSYS仿真軟件進行求解，織針1～3階的模態分析結果如圖8所示。前3階段固有頻率分別為383.1、896.7、1 019.0 Hz。將仿真結果與表1中實際測試值進行比較，比較結果如表2所示。

圖8 織針前3階模態分析結果圖Fig.8 First 3 orders of modal analysis results of knitting needle. (a) Order 1; (b) Order 2; (c) Order 3

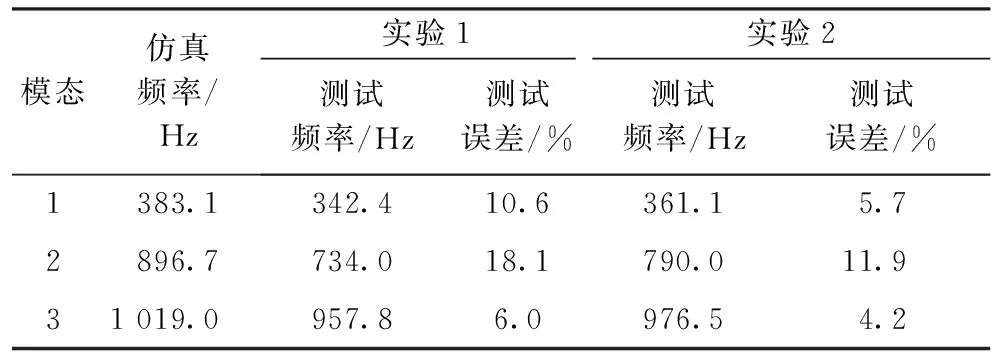
表2 織針仿真與測試結果誤差結果匯總Tab.2 Summary of knitting needle simulation and test results error result

由表2所示數據可知，采用ANSYS仿真分析計算得出的固有頻率值偏大。實驗采用黏合體來代替織針進行固有頻率的求解，額外引進的PZT、焊點、導線等物件增加了織針的質量，且對織針固有頻率的測量產生了不可忽視的作用，織針固有頻率與其質量的關系如式(3)所示：

(3)

式中，Δm為額外引進的物體導致的附加質量。

由式(3)可知，織針模態頻率與質量的平方根成反比，通過在織針中部附加集中質量塊Δm，改變了系統固有頻率，且附加質量越大，織針模態頻率越小。

為了更貼近實驗中黏合體的實際結構模型，本文在原織針三維幾何模型的基礎上，加入PZT結構，形成黏合體幾何模型，并對其進行ANSYS仿真分析，黏合體1～3階的模態分析結果如圖9所示。

圖9示出黏合體做ANSYS仿真計算后第1～3階的模態結果圖，前3階段固有頻率分別為382.0、885.5、986.4 Hz。將仿真結果與表1中實際測試值進行比較，比較結果如表3所示。

相比于表2，其模態頻率更接近實驗值，證明了實驗中額外引進的PZT等物質使得織針固有頻率的測試值較仿真計算值要小。由表2、3所示數據可知，本文研究的緯編針織機織針自由狀態下固有頻率測試方法所得的第1階，第3階固有頻率的測試值相對第2階固有頻率與計算值更為接近，這主要是PZT的額外引入，改變了織針的原有的質量與剛度，導致黏合體各階的固有頻率較織針各階固有頻率產生了偏差。另外，實驗2的測試結果較實驗1更接近計算值，這主要是兩組實驗的黏合體均為人工制造，黏合體的質量，剛度等參數均有細微偏差，故兩組實驗也存在一定的偏差。

本文研究的測試方法所得的固有頻率值與織針計算值雖存在偏差，但偏差的范圍是可接受的，特別是第1階，第3階固有頻率的測試值，最小誤差僅為4.2%。誤差的引入主要是PZT的額外引入導致，選用尺寸更小但壓電效應更強的PZT材料會減少測試數據與計算值的誤差率。

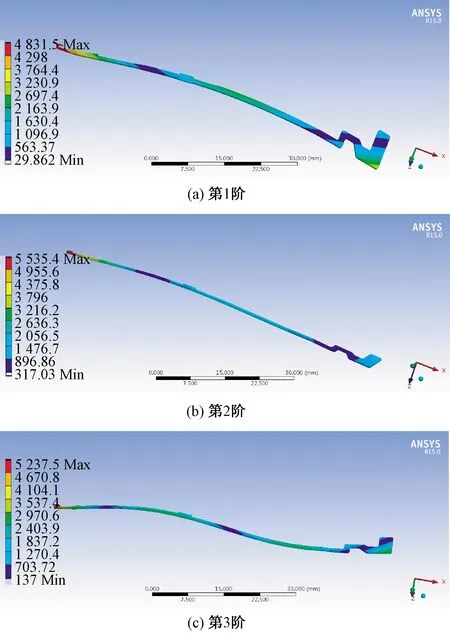
圖9 黏合體前3階模態分析結果圖Fig.9 First 3 orders of modal analysis results of bonded body.(a) Level 1; (b) Level 2; (c) Level 3

4 結束語

緯編針織機編織過程中，織針是編織機構中重要的執行器件。織針編織過程中的振動特性直接影響織物的品質，而織針固有頻率的有效測試是其振動特性研究的前提。本文針對緯編針織機織針結構尺寸微小、細長、橫截面直徑不定等特性，提出了一種黏合體結構，并采用阻抗分析儀對黏合體進行掃頻測試，確定其固有頻率，并以此測試頻率近似估計織針的固有頻率。通過2次實驗的數據對比來驗證本實驗方法的可重復性，并對2組數據的不一致性進行了分析。

本文采用實驗與仿真結合的方式，采用ANSYS軟件對織針的固有頻率進行計算，采用懸臂梁曲率、撓度理論對測振原理進行分析，從而驗證實驗的準確性。對比固有頻率與實際計算值可知，雖存在PZT材料引入帶來的誤差，但本研究的測試方法總體實現了織針固有頻率的有效測量。本文研究的針織固有頻率的測試方法對織針固有頻率的研究以及其他微小尺寸機構固有頻率的測量具有一定借鑒意義。