循環(huán)應力松弛下黃麻織物/聚乙烯復合材料能量耗散演化規(guī)律

汪澤幸， 吳 波， 李 帥， 何 斌

(湖南工程學院 紡織服裝學院， 湖南 湘潭 411104)

麻纖維增強熱塑性復合材料具有低成本、低能耗、廢料可重復利用以及破損后安全性能好等優(yōu)點，在建筑、交通運輸?shù)阮I域應用前景廣闊[1-4]。

目前，已從增強纖維與基體類型、增強體結構形式、麻纖維表面改性處理方法及制備工藝等角度，對麻纖維增強熱塑性復合材料的拉伸性能[2, 5-7]、沖擊性能[6-8]、彎曲性能[5-8]、吸濕/吸水性能[6]、隔音性能[7]、耐老化性能[8-9]、耐熱性能[10]、蠕變與應力松弛性能[11-12]、動態(tài)力學性能[13-14]等進行了較為全面的研究。結果發(fā)現(xiàn)，優(yōu)化麻纖維表面處理方法和復合材料制備工藝可進一步提高麻纖維增強熱塑性復合材料的綜合性能；亦可采用麻纖維與異種纖維制備麻纖維/異種纖維/聚合物復合材料，進一步彌補麻纖維增強熱塑性復合材料的性能不足[15-16]。此外，對麻纖維增強熱塑性復合材料力學性能的研究主要集中在拉伸、彎曲、蠕變與應力松弛等靜態(tài)或準靜態(tài)力學性能方面，而就循環(huán)加載條件下力學性能與能量耗散演化的研究較少[17]。

目前，對紡織品及纖維增強復合材料循環(huán)加載下的力學行為進行研究時，大都集中在無蠕變或應力松弛條件下進行，且較多關注循環(huán)應力或應變、加載速度或頻率和循環(huán)次數(shù)等對應變或應力殘余、模量等宏觀力學性能指標的變化[18-20]，所述性能指標的變化可歸結于循環(huán)加載過程方面中非線性損傷的萌生、擴展與累積[21-23]。復合材料的損傷形式復雜且多樣，包括基體開裂、纖維斷裂、纖維與基體脫黏等。從本質上而言，損傷的萌生、擴展與累積過程是能量非均勻耗散的不可逆過程，材料的循環(huán)加載為能量耗散過程[23-24]，采用能量分析法更能從本質上分析循環(huán)加載過程中材料損傷萌生、擴展與累積的機制與過程，因而采用能量分析法在研究材料循環(huán)加載過程方面具有明顯的優(yōu)越性，可在缺乏深入了解各種損傷與失效機制時對材料循環(huán)加載性能進行總體評估。

基于此，本文采用熱壓法制備黃麻織物/聚乙烯復合材料，并對其循環(huán)應力松弛行為進行測試，分析循環(huán)應力松弛過程中的能量演化規(guī)律。

1 實驗部分

1.1 試樣制備

以商購黃麻織物為增強體，織物組織結構為機織平紋，實測經(jīng)、緯向紗線的線密度均為240 tex，經(jīng)、緯向紗線密度分別為68、58根/(10 cm)，面密度為315.6 g/m2。

熱壓前，將黃麻織物在90 ℃條件下干燥2 h，以充分去除黃麻織物中的水分。采用自行搭建的熱壓設備制備熱塑性復合材料，單層黃麻織物雙面鋪設厚度為0.50 mm的聚乙烯膜，160 ℃下預熱15 min，1 MPa熱壓壓力條件下保壓15 min，后在保壓條件下自然冷卻，獲得黃麻織物/聚乙烯復合材料，實測成品厚度為1.60 mm。

沿黃麻織物經(jīng)、緯向制備矩形試樣，試樣寬為25 mm，長為200 mm，有效夾持隔距為100 mm。

1.2 實驗方法

在WDW-20C型微機控制電子萬能試驗機上自動進行加載—應力松弛—卸載—應力松弛循環(huán)。實驗過程為：以1 mm/min的加載速率加載至循環(huán)應力峰值(σmax)并保持應變一定時間，以同等速率卸載至循環(huán)應力下限(σmin)并保持應變一定時間，即每一循環(huán)中的加載和卸載完成后均歷經(jīng)應力松弛過程，設定循環(huán)次數(shù)為30次。為確保循環(huán)實驗過程中試樣處于拉伸狀態(tài)，并考慮本文篇幅，各次循環(huán)的下限應力均設定為0.8 N/mm2。所有實驗均在環(huán)境溫度為(20±1)℃、 相對濕度為(65±2)%的條件下進行。

2 實驗結果與分析

2.1 應力與應變曲線分析

循環(huán)應力峰值為12.5 N/mm2，應力松弛時間tr為1 800 s時，經(jīng)、緯向試樣的應力與應變曲線如圖1所示。可知，因黃麻織物/聚乙烯復合材料的非線性、黏彈性特性以及加載過程中材料產(chǎn)生不可逆的塑性變形，卸載曲線不沿加載曲線路徑返回，同一循環(huán)過程中，加、卸載終點并不重合，加載-應力松弛-卸載-應力松弛曲線并不封閉，且隨著循環(huán)次數(shù)N的增加，加載和卸載終點逐漸向右偏移。

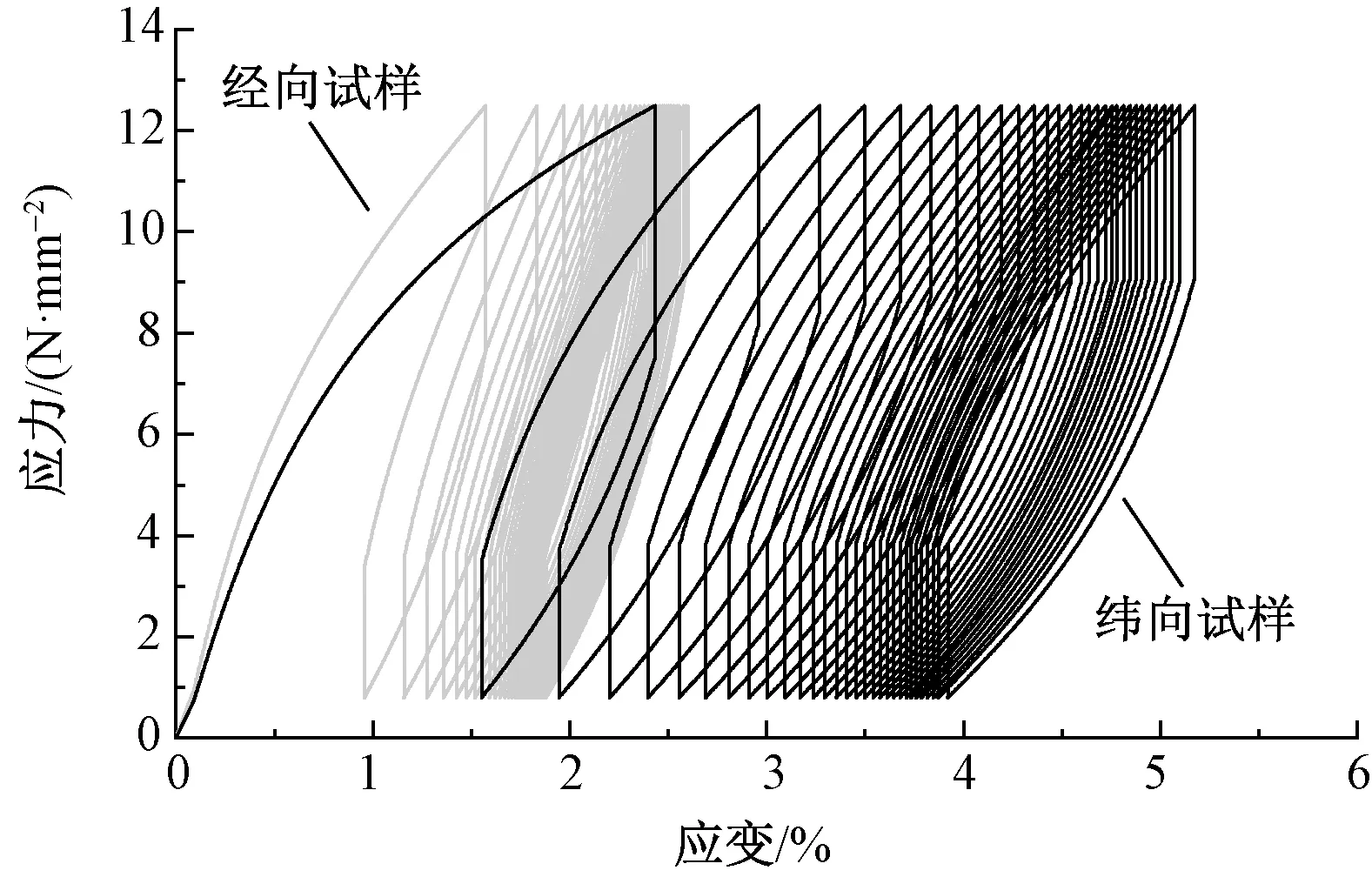
圖1 經(jīng)緯向試樣應力與應變曲線Fig.1 Stress and strain curves of warp and fill specimens

從圖1中還可看出，除第1個循環(huán)產(chǎn)生的殘余應變量較大以外，從第2個循環(huán)開始，各循環(huán)產(chǎn)生殘余應變量逐漸減少并趨于穩(wěn)定。在循環(huán)的初始階段，各循環(huán)的應力與應變曲線較為稀疏，隨著循環(huán)次數(shù)的增加，各循環(huán)的應力與應變曲線逐漸密集，體現(xiàn)由稀疏到密集的發(fā)展過程。

2.2 經(jīng)緯向能量演化對比

從能量變化的角度而言，加載曲線下方面積代表材料吸收的總應變能，卸載曲線下方面積代表材料的可恢復彈性應變能，而加載曲線和卸載曲線下方面積之差為該循環(huán)的耗散量，即塑性應變能。

W=We+Wp

(1)

式中：W、We與Wp分別為總應變能、彈性應變能與塑性應變能，mJ/mm3。

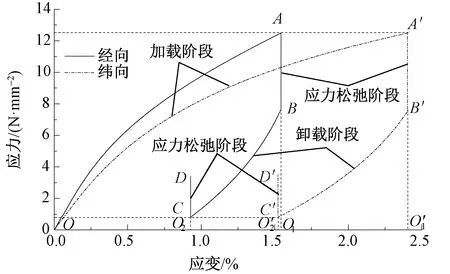
圖2 經(jīng)緯向試樣第1個循環(huán)Fig.2 First cycle of warp and fill specimens

為表征循環(huán)過程中應變能的轉化趨勢，定義同一循環(huán)中彈性應變能We與總應變能W的比值為可恢復應變能系數(shù)Ke，塑性應變能Wp與總應變能W的比值為不可恢復應變能系數(shù)Kp。

Ke=We/W

(2)

Kp=Wp/W

(3)

經(jīng)、緯向試樣各循環(huán)的應變能(W、We與Wp)、應變能系數(shù)(Ke、Kp)如圖3所示。

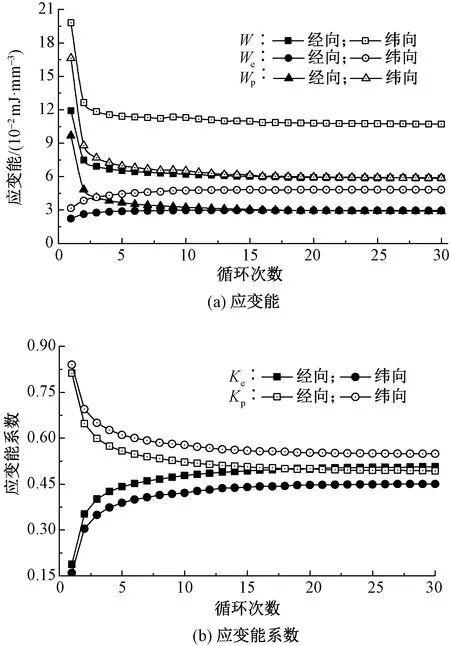
圖3 經(jīng)緯向試樣應變能與應變能系數(shù)Fig.3 Strain energy(a) and strain energy factor(b) of warp and fill specimens

由圖3可知，循環(huán)次數(shù)N增加，經(jīng)、緯向試樣的總應變能W與塑性應變能Wp先快速降低后趨于穩(wěn)定，而彈性應變能We則與之相反，且相對于經(jīng)向試樣，緯向試樣的應變能(W、We、Wp)較高。

由圖3還可看出，循環(huán)次數(shù)N增加，經(jīng)、緯向試樣的可恢復應變能系數(shù)Ke逐漸增加，而不可恢復應變能系數(shù)Kp則與之相反；相同循環(huán)次數(shù)時，相對于緯向試樣，經(jīng)向試樣的不可恢復應變能系數(shù)Kp較高，但可恢復應變能系數(shù)Ke較低。

綜合圖1、3可發(fā)現(xiàn)，經(jīng)、緯向試樣的循環(huán)曲線、應變能與應變能系數(shù)變化曲線形態(tài)高度相似，表明循環(huán)應力松弛下，經(jīng)、緯向試樣的變形與能量耗散機制相同，故后續(xù)以經(jīng)向試樣為研究對象，深入分析循環(huán)應力松弛條件下的能量演化規(guī)律與機制。

2.3 應力松弛時間對能量耗散的影響

循環(huán)應力峰值為12.50 N/mm2，應力松弛時間tr分別為0、100以及1 800 s時，經(jīng)向試樣的應變能、應變能系數(shù)曲線分別如圖4、5所示。

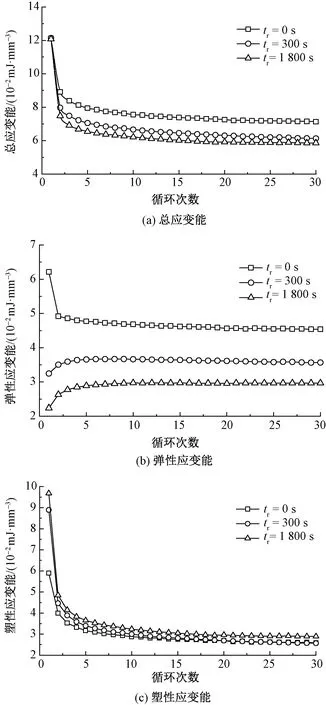
圖4 不同應力松弛時間下應變能曲線Fig.4 Strain energy curves at different stress relaxation time(a) Total strain energy; (b) Elastic strain energy; (c) Plastic strain energy

由圖4可知，不同應力松弛時間tr時，循環(huán)次數(shù)(N) 增加，總應變能W(N≥2時)與塑性應變能先快速下降后趨于穩(wěn)定。無應力松弛(tr=0)階段時，彈性應變能隨循環(huán)次數(shù)的增加先快速下降后趨于穩(wěn)定；而有應力松弛(tr>0)階段時，彈性應變能則先快速增加后趨于穩(wěn)定。

由圖5可知，可恢復應變能系數(shù)Ke隨循環(huán)次數(shù)的增加而增加，而隨應力松弛時間tr的增加而降低，但不可恢復應變能系數(shù)Kp則與之相反。

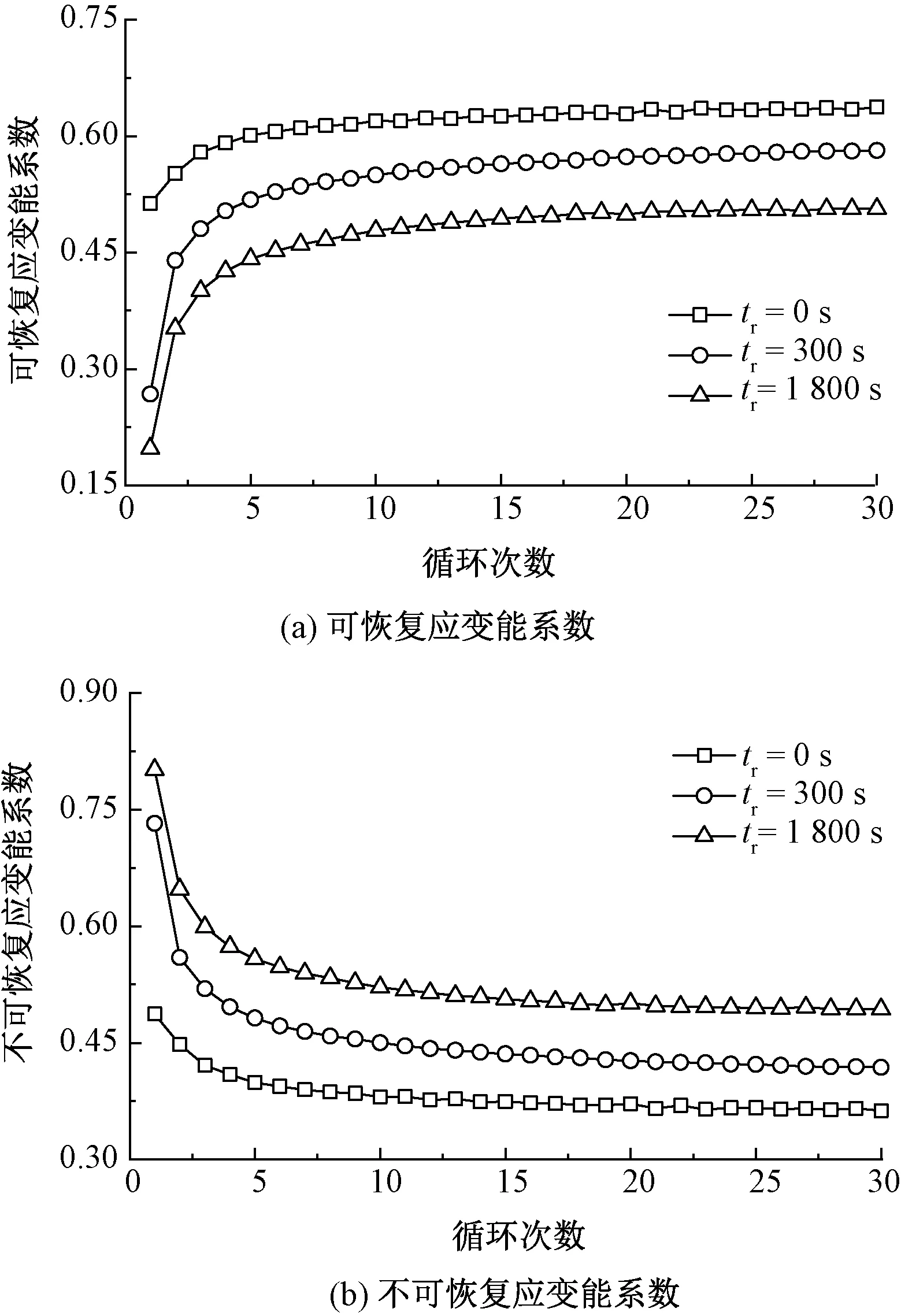
圖5 不同應力松弛時間下應變能系數(shù)曲線Fig.5 Strain energy factor curves at different stress relaxation time. (a) Recoverable strain energy factory;(b) Unrecoverable strain energy factory

應變能與應變能系數(shù)呈現(xiàn)上述變化趨勢，主要是由于應力松弛過程中增強體纖維和基體聚乙烯大分子鏈間的相對滑移與空間形態(tài)變化所致。以不同應力松弛時間的第1個循環(huán)(見圖6)為例，分析應力松弛時間對應變能和應變能系數(shù)的影響。

圖6 不同應力松弛時間下經(jīng)向試樣第1個循環(huán)Fig.6 First cycle of warp specimens at different stress relaxation time

由圖6可知，因試樣加載至同等循環(huán)應力峰值，加載曲線下方面積應相等，即總應變能應相等，但因試樣中紗線力學性能的非均勻性以及試樣寬度存在小幅度差異，導致總應變能存在小幅度差異，但差異不明顯。循環(huán)次數(shù)增加，增強體纖維和基體聚乙烯中大分子鏈的可滑移程度降低，增強體與基體之間可脫黏的點數(shù)量減少，同時，織物中紗線的屈曲結構的不可逆改變程度減少，故循環(huán)加載過程中，試樣的變形主要為增強纖維和基體聚乙烯大分子鏈的可回復變形以及增強體可回復屈曲結構變形，宏觀表現(xiàn)為總應變能持續(xù)降低。

無應力松弛(tr=0)階段時，即試樣加載至循環(huán)應力峰值后立即卸載，循環(huán)加載過程中的塑性應變能，主要由加載過程中增強纖維與基體聚乙烯中大分子鏈間產(chǎn)生的滑移、增強體與基體間脫黏以及織物中紗線屈曲結構不可逆改變而產(chǎn)生。而在卸載階段，外加載荷持續(xù)降低，增強體纖維和基體聚乙烯中大分子鏈在內(nèi)應力作用下持續(xù)回復，大分子鏈間滑移較少，因而少有能量的耗散；隨循環(huán)加載的進行，增強體纖維與基體大分子鏈之間的可滑移程度、增強織物結構的不可逆變形逐漸減少，可逆的彈性變形比例增加，從而宏觀表現(xiàn)為不可逆的塑性應變能以及可恢復應變系數(shù)持續(xù)減小，而可逆的彈性變形能及可恢復應變系數(shù)持續(xù)增加。

存在應力松弛(tr> 0)階段時，即試樣加載至循環(huán)應力峰值后保持對應的應變不變，在增強纖維與基體的大分子鏈向內(nèi)收縮應力作用下，大分子鏈之間產(chǎn)生滑移并在新的位置建立較為穩(wěn)定的結合，且大分子鏈在應力作用下其構象持續(xù)調(diào)整，導致大分子鏈的向內(nèi)收縮應力持續(xù)降低。后續(xù)卸載階段，因大分子鏈間產(chǎn)生滑移導致大分子鏈回復量減少，宏觀表現(xiàn)為卸載曲線下移，卸載曲線下方面積減少，即可恢復的應變能減少。后續(xù)循環(huán)加載過程中，試樣的變形主要為增強纖維與基體大分子鏈和增強體織物結構的可回復變形，且隨循環(huán)加卸載次數(shù)的增加，可回復變形的比例增加，從而導致卸載階段可回復的彈性應變能持續(xù)增加，且可恢復應變能系數(shù)持續(xù)增加。

循環(huán)應力松弛過程中，隨應力松弛時間的增加，纖維與基體的大分子鏈空間結構調(diào)整時間越長、大分子鏈之間的滑移程度越充分，應力松弛量增加，大分子鏈的可逆彈性變形比例減少，導致回復曲線下移程度增加，回復曲線下方面積越小，即可恢復彈性應變能越小，且可恢復應變能系數(shù)降低，加載與卸載曲線之間的面積增加，即不可回復的塑性應變能與不可恢復應變能系數(shù)增加。

2.4 循環(huán)應力峰值對能量耗散的影響

應力松弛時間tr為1 800 s，循環(huán)應力峰值σmax分別為6.25、12.50、18.75 N/mm2時，經(jīng)向試樣的應變能曲線如圖7所示。

圖7 不同循環(huán)應力峰值下應變能曲線Fig.8 Curves of strain energy at different peak cyclic stress.(a) Total strain energy; (b) Elastic strain energy;(c) Plastic strain energy

由圖7可知，隨循環(huán)次數(shù)的增加，不同循環(huán)峰值應力下，總應變能與塑性變形能均先快速下降后趨于穩(wěn)定，而彈性應變能則與之相反。且循環(huán)應力峰值越高，試樣的總應變能、彈性應變能與塑性應變能越高。

圖8示出不同循環(huán)應力峰值時的應變能系數(shù)曲線。可知：隨循環(huán)次數(shù)的增加，可恢復應變能系數(shù)(Ke)呈現(xiàn)增加趨勢，而不可恢復應變能系數(shù)(Kp)則呈現(xiàn)降低趨勢；相同循環(huán)次數(shù)時，可恢復應變能系數(shù)隨循環(huán)應力峰值的增加而增加，而不可恢復應變能系數(shù)則與之相反。

圖8 不同循環(huán)應力峰值σmax下應變能系數(shù)曲線Fig.8 Curves of strain energy factor at different peak cyclic stress. (a) Recoverable strain energy factory; (b) Unrecoverable strain energy factory

以不同循環(huán)應力峰值時經(jīng)向試樣的第1個循環(huán)，分析循環(huán)應力峰值對應變能和應變能系數(shù)的影響，結果如圖9所示。

圖9 不同循環(huán)峰值應力下經(jīng)向試樣第1個循環(huán)Fig.9 First cyclic of warp specimens at various peak cyclic stress

由圖9可知，隨循環(huán)應力峰值增加，加載過程中，由于增強體纖維和基體大分子鏈的伸直與滑移程度增加，紗線屈曲結構改變程度增加，且增強體中纖維與基體之間脫黏點數(shù)量增加，因而宏觀表現(xiàn)為循環(huán)應力峰值力對應的應變增加，加載曲線下方面積增加，即試樣的總應變能增加。

另外，循環(huán)應力峰值越高，應力松弛量也越高。表明高循環(huán)應力峰值時，增強體纖維與基體中大分子鏈伸直和伸長程度較高，大分子鏈在高內(nèi)應力作用下產(chǎn)生的滑移程度較高，消耗的應變能較高。因高循環(huán)峰值應力時，加載和應力松弛階段大分子鏈間的滑移程度增加，導致塑性應變能與不可恢復應變能系數(shù)增加。試樣加載至循環(huán)應力峰值并經(jīng)過應力松弛后，高循環(huán)應力峰值時，試樣中的殘余應力較高，表明增強纖維與基體中大分子鏈的伸直和伸長程度也較高，即試樣中存儲的可逆彈性應變能亦較高，但因高循環(huán)峰值應力時，增強纖維和基體中大分子鏈滑移程度較高，導致卸載過程中，大分子鏈中可回復應變的比重減少，從而導致可恢復應變能系數(shù)較低。

隨循環(huán)次數(shù)的增加，增強體纖維與基體聚乙烯大分子鏈之間的可滑移量以及增強體與基體之間可脫黏的點數(shù)量逐漸減少，試樣變形主要為增強纖維和基體聚乙烯大分子鏈的可回復變形以及增強體可回復屈曲結構變形構成。故而，宏觀表現(xiàn)為隨循環(huán)次數(shù)增加，總應變能、塑性應變能、不可恢復應變能系數(shù)持續(xù)降低，而彈性應變能與可恢復應變能系數(shù)持續(xù)增加。

3 結 論

本文以黃麻織物為增強體，以聚乙烯為基體，采用熱壓法制備黃麻/聚乙烯復合材料，并對其循環(huán)應力松弛行為進行了測試，分析了循環(huán)應力松弛過程中試樣的應變能(總應變能、彈性應變能、塑性應變能)與應變能系數(shù)(可恢復與不可恢復應變能系數(shù))的變化規(guī)律，主要結論如下：

1)經(jīng)、緯向試樣的應力與應變曲線形態(tài)相似，隨循環(huán)次數(shù)的增加，各循環(huán)的應變能參數(shù)(總應變能、彈性應變能與塑性應變能)與應變能恢復系數(shù)(可恢復與不可恢復應變能系數(shù))的變化趨勢一致，表明循環(huán)應力松弛下，黃麻織物/聚乙烯復合材料經(jīng)緯向的變形與能量演化機制是一致的。

2)循環(huán)應力松弛條件下，黃麻織物/聚乙烯復合材料的應變能(總應變能、彈性應變能與塑性應變能)以及應變能系數(shù)(可恢復與不可恢復應變能系數(shù))變化規(guī)律較為復雜，其不僅受應力松弛時間、循環(huán)應力峰值的影響，同時還與循環(huán)次數(shù)密切相關。值得關注的是，循環(huán)加載過程中，應力松弛階段的有無將改變彈性應變能的變化趨勢；無應力松弛階段的簡單循環(huán)加載條件下，彈性應變能呈現(xiàn)逐漸減低的變化趨勢，而循環(huán)應力松弛條件下，彈性應變能的變化趨勢則與之相反。

本文僅對黃麻織物/聚乙烯復合材料在不同應力松弛時間、循環(huán)應力峰值條件下的能量演化規(guī)律進行了分析，為全面把握麻纖維增強熱塑性復合材料在循環(huán)應力松弛條件下的力學行為、能量耗散演化規(guī)律，有必要針對增強纖維類型、增強體結構形式、制備工藝、測試參數(shù)等對麻纖維增強熱塑性復合材料的變形特性、應力松弛特性以及能量演化規(guī)律進行深入研究。