混凝土楔形體在水電站導流圍堰穩定性優化中的應用

黃 亮

(江西省宜春市水利水電工程監理有限公司，江西 宜春 336000)

0 引 言

圍堰指的是在水利工程建設中，為了建造永久性水利設施而修建的臨時性維護結構。其作用是防止水和土進入修建位置，方便圍堰內部排水工作，為開挖基坑準備基礎工作。圍堰主要用于水工建筑中，一般在用完后拆除。圍堰屬于一種臨時性擋水建筑物，對于結構來講需要具有穩定、防滲、抗沖的性能[1]。在施工技術上，要方便使用后的拆卸，結構布局上水流平順。楔形體下底面是梯形或平行四邊形，上底面變成與下底面平行邊平行的線段的一種擬柱體。過流圍堰是指在一定條件下允許堰頂過水的圍堰，過流圍堰可以承擔擋水任務，一般建設在洪枯流量比值大，水位變幅顯著的河流。水電站導流圍堰受到很多外部因素的干擾，為此研究混凝土楔形體在水電站導流圍堰穩定優化中的應用，利用混凝土楔形體硬度大的優點，增強圍堰的穩定性[2]。國內外施工水電站采用過流圍堰的形式較多，國外早在1966年就已開始過流圍堰工程的設計研究，截至到目前，已經建造成多種過流圍堰工程，有著成熟的知識理論體系。國內也已經形成諸多的導流圍堰工程，構建出多種行之有效的研究理論，增強了水電站工作過程的安全[3]。

1 混凝土楔形體在水電站導流圍堰穩定性優化中的應用

1.1 控制圍堰開裂特征參數

混凝土楔形體在水電站導流圍堰運用時，導流圍堰分布著一個滲流場，圍堰的滲透系數較小，所以設定其量級為1E-10 m/s,圍堰在接縫處的單位寬度流量就可表示為：

(1)

其中：b為圍堰寬度；v為運動黏滯系數；vb為裂縫處的滲流速度；J為圍堰裂縫處水力坡降；g為重力加速度。

在相同的滲透系數下，根據達西定理，混凝土楔形體在圍堰中表現出的流量數值va就可計算為：

(2)

式中：k為滲透系數。

將上述兩項滲透計算公式聯立，得到混凝土楔形體運用后的滲透系數表達式：

(3)

式中：各個參數含義不變。

在上述滲透參數的控制下，選用不同水電站過流圍堰的參數，見表1。

在表1所示的各項參數下，將導流圍堰按照實體單元處理，以式(3)的滲透系數為參考，構建導流圍堰局部的數值模型坐標系，見圖1。

表1 不同水電站過流圍堰的參數

圖1 數值模型坐標系

以圖1所示的數值模型為研究對象，導入表1中的各項系數至數值模型坐標中，模擬不同控制混凝土楔形體的開裂縫數值大小，匯總不同縫寬數值下產生的裂縫數量，見表2。

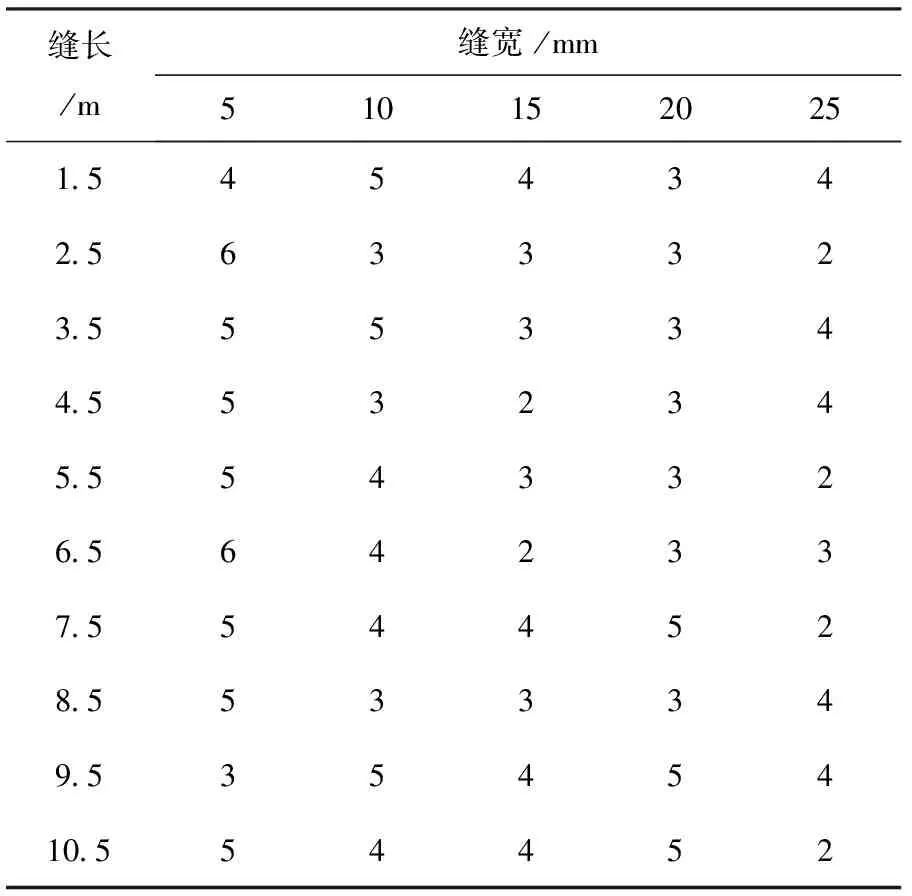
表2 模型不同縫寬產生的裂縫數量

由表2所示的數值可知，在不同縫寬數值下，裂縫數量基本可以維持在數值6及以下[4]。以表2中最大縫長及縫寬數值為自變量，構建開裂優化方程，開裂優化方程可表示為：

(4)

其中：L為裂縫長度；D為開裂深度；a為混凝土楔形體的強度；c為混凝土楔形體水泥含量。

按照上述計算公式優化導流圍堰開裂特征參數，降低裂縫對圍堰穩定性的破壞[5]。對開裂參數優化后，控制圍堰導流過程的滲透量，最終計算得到混凝土楔形體在水電站穩定優化中的穩定系數[6]。

1.2 減少導流滲透量

采用上述優化后的開裂特征參數，在圖1的模型中，計算過流水體的壓力水頭數值，計算公式可表示為：

(5)

其中：h為圍堰的水體高度；c為圍堰水體的流量參數；s為圍堰的橫截面積；其余參數含義保持不變。

過流圍堰不同數值的開裂縫寬有著不同的壓力水頭[7]，假設圍堰堰體分邊界水頭分布存在兩種邊界，數量關系可表示為：

(6)

式中：x,y,z均為分界位置數值；κ為分邊界；t為導流時間；φ為分布函數；其余參數含義不變。

當過流圍堰出現隔水邊界時，式(6)中q=0，水壓的各向滲透系數相等[8]，此時水體的壓力水頭數值就是z。但在實際水電站導流圍堰中，還常常包含流量邊界，此時流量邊界就可表示為：

(7)

式中：f為流量；其余參數含義不變。

結合上述得到的邊界數量關系，得到導流圍堰的壓力水頭等值線，見圖2。

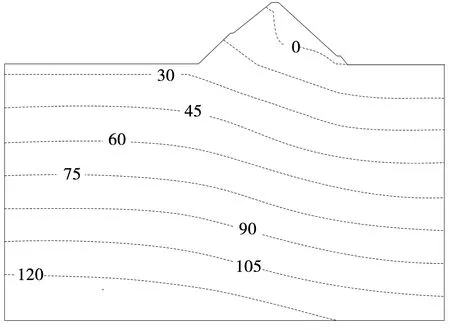
圖2 壓力水頭等值線

以圖2所示的壓力水頭等值線相等的數值為相同的水流流向，在相同水流方向上，采用摩爾-庫倫模型分析相同水流方向導流在圍堰產生的滲透量[9]，在混凝土楔形體的參與下，計算滲透量的主應變增量，數量公式可表示為：

(8)

式中：e為混凝土楔形體產生的彈性；p為塑性應變；ε為形變參數。

根據廣義的胡克定律，計算該部分水壓在不同方向產生的應變增量，計算公式可表示為：

(9)

式中：σ為增量數值；下角標1,2,3分別為模型的不同坐標方向；α1、α2分別為彈性系數，存在如下數量關系：

(10)

式中：K為上下游水頭差；G為水體滲透速度。

在使用混凝土楔形體穩定優化過流圍堰時，當混凝土楔形體的剪應力達到臨界值時，穩定優化過程會進入屈服狀態[10]，該狀態可表示為：

|τn|=g(σn)

(11)

上述數量關系中，混凝土楔形體在實際應用時，可根據不同狀態的臨界值，控制不同屈服狀態[11]，進而控制水體的導流滲透量，維持圍堰的穩定。

1.3 優化穩定系數

在應用混凝土楔形體后，以上述計算得到的開裂系數與滲透量數值為基礎，將此時穩定優化過程視為折線型實用堰計算，計算得到堰上頭水H。計算公式可表示為：

(12)

其中：γ為淹沒系數；m0為流量系數；B為河道寬度；Q為單位流量。

在該數量值的控制下，長時間的水流沖擊會在圍堰處形成沖擊坑[12]，混凝土楔形體會在圍堰下游形成一個穩定消力池，穩定過程可表示為：

(13)

其中：q為水頭損失；h為圍堰首端水深；d為混凝土楔形體半徑；y為水體的流經距離；s為水體流經時間。

根據上述計算處理公式，在混凝土楔形體的參與下，控制得到不同穩定系數[13]，圍堰的穩定性系數變化見圖3。

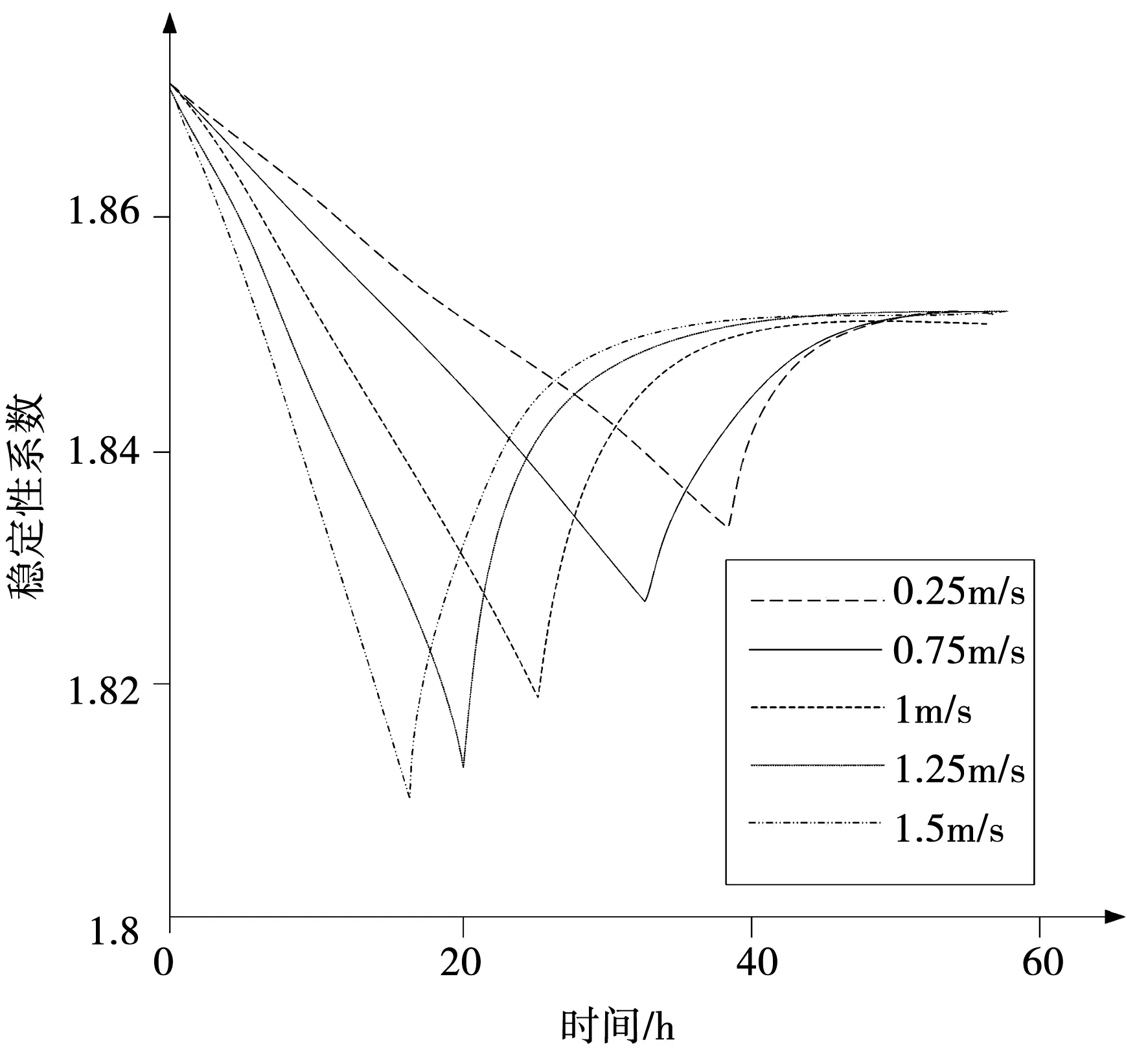
圖3 穩定性系數變化

由圖3所示的穩定性系數變化規律可知，隨著混凝土楔形體控制得到的流速數值不斷增大[14]，穩定性數值也就越小。在實際使用混凝土楔形體穩定優化水電站導流圍堰時，引入一個動能校正系數[15]，進而控制圍堰水流的速度，將水電站的圍堰劃分為不同的區段，計算不同區段的消能率。計算公式可表示為：

(14)

其中：E1為一區段的消能率；E2為二區段的消能率；E0為總區段的消能率。

在實際優化時，從水電站的下游河道開始，逐級向導流圍堰的上游計算，最終完成對穩定系數的優化。綜合上述處理，最終完成研究分析。

2 實 驗

2.1 實驗準備

實驗采用混凝土原材料制成3種不同的混凝土楔形體用于實驗，混凝土的配比情況見表3。

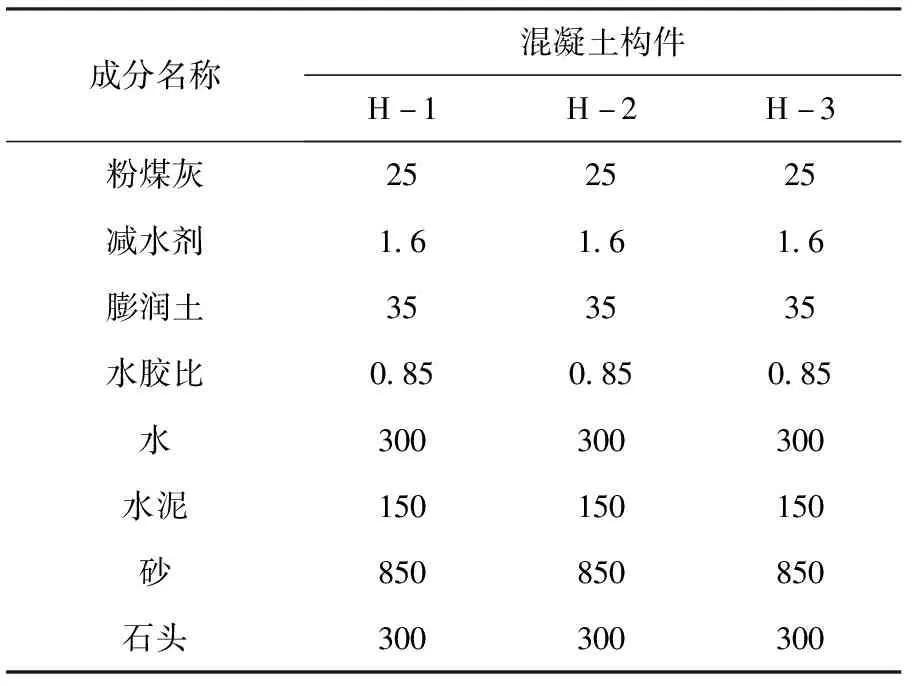
表3 混凝土含量配比

如表3所示的配比制成3種相同配比的混凝土楔形體，計算混凝土楔形體在實際使用時的各項性能參數。性能參數見表4。

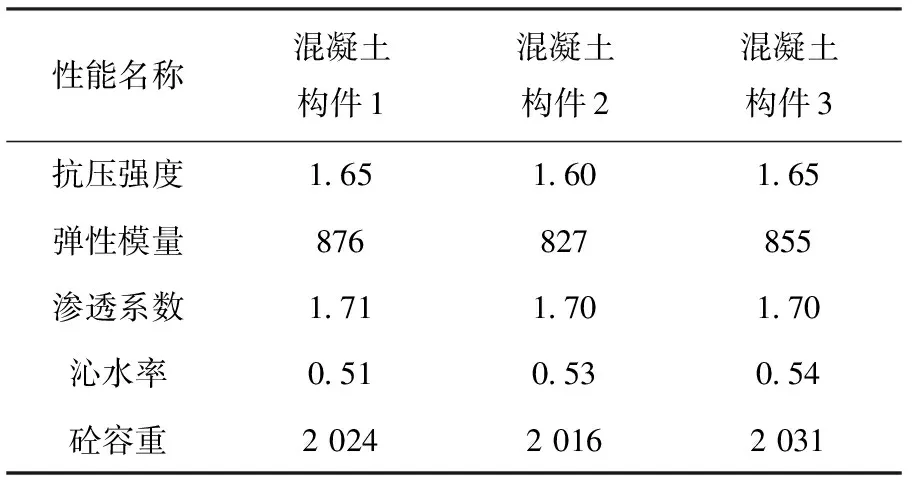
表4 混凝土構件性能參數

在上述性能參數的控制下，采用圖4所示的圍堰布置結構進行實驗。

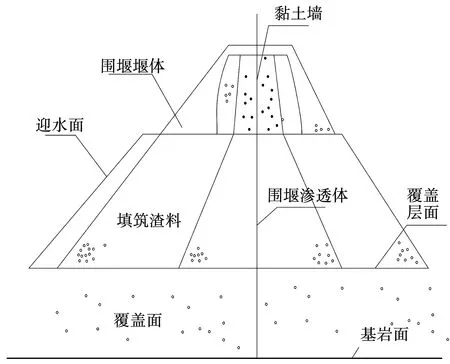
圖4 導流圍堰布置結構

在圖4所示的圍堰布置結構中，控制圍堰堰體的水流速度維持在0.5 m/s的上升速度，計算未使用混凝土楔形體前圍堰的穩定性系數，并使用一種傳統應用方法與文中研究的應用方法進行對比，對比3種應用方式的性能。

2.2 結果及分析

基于上述實驗準備，設定水電站內的水流速度為0.5 m/s上升方向，實驗時間為50 h，設定開裂測量時間點每隔5 h測量一次，以圍堰堰體的開裂數值為對比標準，在不同應用條件下，圍堰的開裂數值結果見表5。

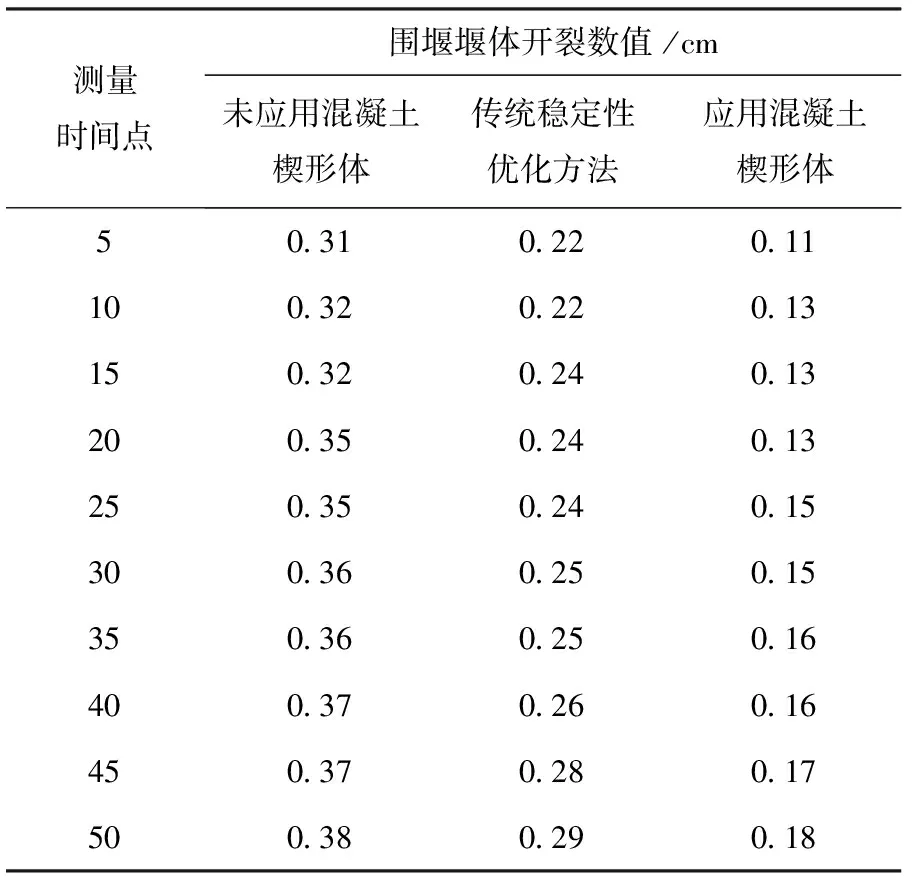
表5 圍堰堰體開裂數值

由表5所示的圍堰堰體開裂數值可知，3種不同的應用條件對圍堰堰體有著不同程度的剪切力，不同的剪切力形成不同的開裂數值。未使用混凝土楔形體行穩定性優化方法形成的開裂數值較大，在最終測量時間點形成的開裂系數為0.38 cm，開裂數值最大；采用傳統穩定性優化方法的圍堰堰體最終形成的開裂數值為0.29，開裂數值較小；而文中應用了混凝土楔形體的穩定優化方法最終形成的開裂數值為0.18。綜合上述對開裂數值的研究可知，應用了混凝土楔形體的穩定性優化方法能夠有效地控制圍堰堰體的開裂系數。

保持上述實驗環境不變，在3種不同的穩定性優化條件下，采用瑞典圓弧法計算圍堰的安全性系數，計算公式如下：

(15)

其中：F為安全系數；MR為抗滑力矩；Ms為土體繞圓心下滑的滑動力矩。

根據上述計算公式，取應用3種不同性能系數的混凝土楔形體的平均值作為最終的穩定性系數，最終得到3種應用條件下的穩定性數值。穩定性數值結果見圖5。

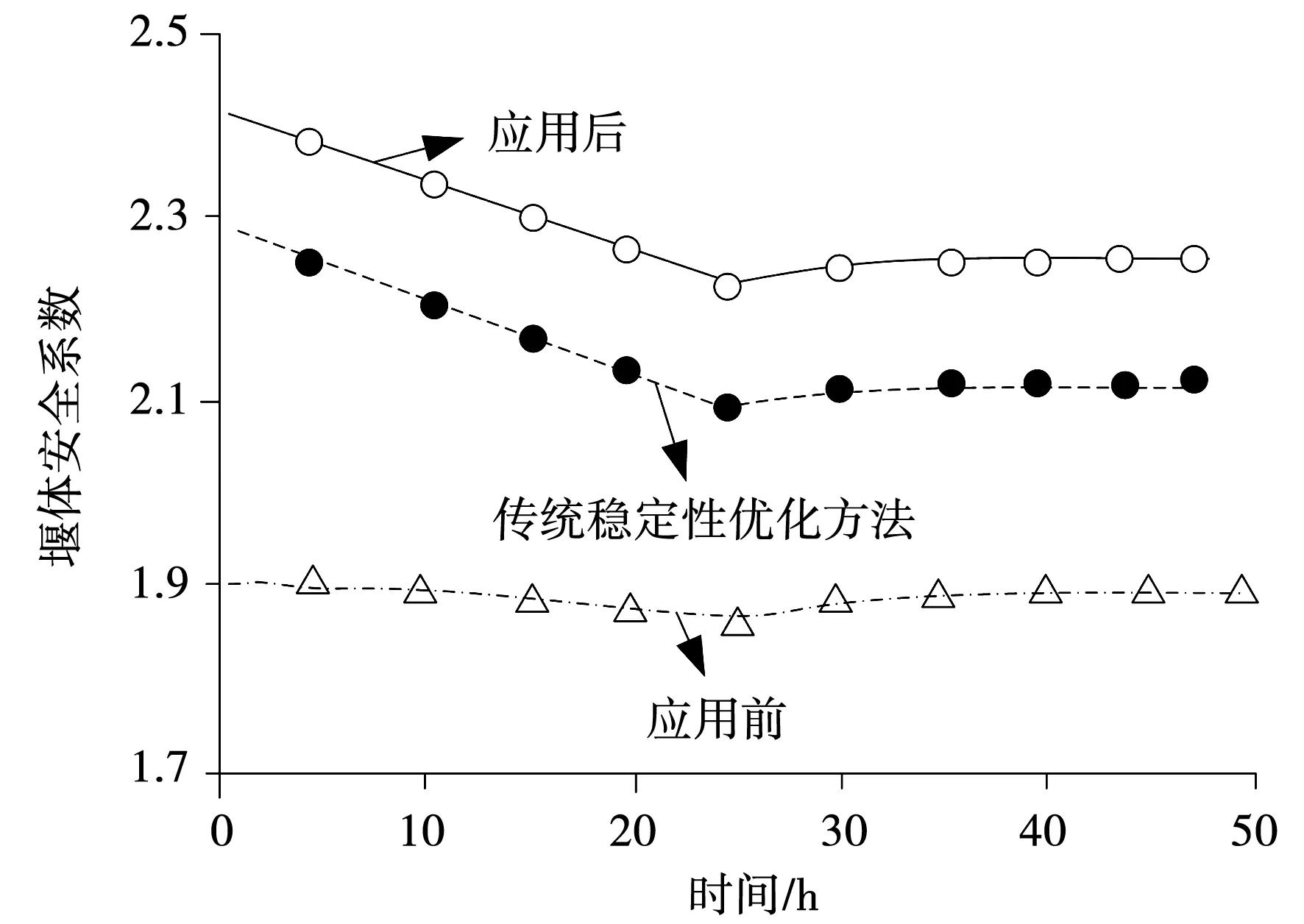
圖5 安全系數變化

由圖5所示的安全系數變化可知，在直接對水電站導流圍堰穩定性進行優化時，水電站導流圍堰的安全系數在1.9左右，安全系數數值最小；在應用傳統穩定優化方法時，計算得到的安全系數在2.1左右，要比穩定性優化時未使用混凝土楔形體時的安全性數值要大；而穩定優化過程中應用了混凝土楔形體的應用方法最終得到的平均安全數值為2.3左右，綜合上述安全數值，文中研究的應用方法得到的圍堰安全數值更大。

3 結 語

水電站導流圍堰的穩定是水電站正常發電工作的重要前提，混凝土楔形體在圍堰過程中能夠起到穩固圍堰穩定性的作用，為此研究混凝土楔形體在水電站導流圍堰穩定優化中的應用。利用混凝土楔形體來優化圍堰的穩定性，能夠改善傳統穩定性優化方法開裂數值過大、圍堰安全數值過低的不足，具有一定的實用性。