攔截機動目標的多導彈協同制導律
馬萌晨 宋申民










摘 要:面向多導彈協同攔截機動目標的問題, 基于剩余飛行時間控制, 設計了兩種不同的協同制導律。 針對多導彈分布式通信的場景, 基于偏置比例導引的思想設計了具有時變導航系數的分布式協同比例制導律; 針對指定攻擊時間的場景, 基于常值前置角下的剩余飛行時間形式, 利用滑模控制和非線性擾動觀測器設計了具有指定攻擊時間的滑模制導律。 仿真結果表明, 所設計的兩種制導律可以有效針對機動目標實施協同攻擊或依次攻擊。
關鍵詞:???? 機動目標; 剩余飛行時間; 偏置比例導引; 非線性擾動觀測器; 滑模控制; 多導彈協同; 制導律
中圖分類號:???? TJ765.3; V448? 文獻標識碼:??? A? 文章編號:???? 1673-5048(2021)06-0019-09
0 引? 言
現代戰爭是體系與體系之間的對抗, 隨著通信組網技術的發展, 多導彈協同作戰正逐步成為現代戰場中的重要作戰模式之一。 多導彈之間通過通信實現對目標的協同感知、 協同探測與協同攻擊, 可以最大限度地利用和協調導彈系統資源, 提高導彈的整體作戰效能。
在多導彈協同制導律設計方面, 國內外相關學者進行了大量的研究。 文獻[1]較早開展了攻擊時間控制的研究, 針對反艦導彈, 基于最優控制理論, 通過在傳統比例制導律的基礎上增加攻擊時間誤差反饋項, 設計了多導彈攻擊時間協同制導律, 并給出導彈剩余飛行時間的近似求法。 在此基礎上, 文獻[2]增加了具有終端攻擊角約束的附加項, 實現了同時具有攻擊角度和攻擊時間控制的協同制導律。 文獻[3]通過引入剩余飛行時間方差的概念, 設計了分布式時間協同制導律, 并給出一種剩余飛行時間形式的理論推導。 文獻[4]通過設計含有攻擊時間誤差和導彈前置角的新型滑模面, 設計了攻擊時間可控的滑模制導律, 但該制導律存在不連續的問題。 文獻[5]直接將攻擊時間誤差設計為滑模面, 并通過引入一個連續的非線性函數, 設計了攻擊時間可控的非奇異滑模制導律。 文獻[6]針對導彈在三維空間攻擊固定目標場景, 考慮導彈飛行過程中的視場角約束, 基于一致性算法設計了帶有視場角約束的三維時間協同制導律。 文獻[7]為減少由于剩余飛行時間估計不準產生的誤差, 基于領從式制導架構, 將制導律的攻擊時間控制問題轉換為從彈跟蹤領彈的剩余彈目相對距離問題, 并通過解耦得到俯仰和偏航通道的控制量。 文獻[8]基于領從架構, 采用超螺旋控制方法設計了攻擊時間控制制導律, 提高了所設計制導律的魯棒性與平穩性。 文獻[9]在具有角度約束的最優制導律基礎上, 引入攻擊時間控制修正量, 通過在線的調整領彈和從彈, 設計了具有攻擊時間和角度約束的協同制導策略。 文獻[10]針對高超聲速飛行器, 在滑翔段通過設計兩階段的協同航跡規劃, 實現了攻擊時間和攻擊角度的約束, 該方法為調整導彈的攻擊時間和攻擊角度提供了新的思路。 但上述方法大多是針對艦船等靜止或低速移動目標所設計, 對于運動及機動目標缺乏嚴謹有效的理論分析。
在針對運動目標的協同制導律設計方面, 文獻[11]針對低速運動目標, 通過將目標運動引起的剩余飛行時間變化視為擾動, 利用線性擴張狀態觀測器對其估計并進行補償, 基于固定時間收斂控制理論, 設計了攻擊時間控制協同制導律。 文獻[12]基于滑模控制, 設計了一種可指定攻擊時間的非奇異滑模制導律, 并在此基礎上, 采用虛擬目標的設計思路, 將制導律擴展到機動目標的應用場景中。? 文獻[13]針對靜止和機動目標,? 分別設計了分布式和集中式的協同制導律, 但缺乏嚴謹的理論分析和證明。 文獻[14]基于導彈和運動目標的相對運動學模型, 推導了一種新型的剩余飛行時間形式, 并設計了針對運動目標和機動目標的攻擊時間控制制導律。 文獻[15-16]基于一致性理論, 利用滑模控制方法針對機動目標分別從視線和視線法向方向設計制導律來控制導彈的攻擊時間和攻擊角度, 但該方法要求導彈軸向推力可控, 條件太過苛刻。 文獻[17]研究了切換通信拓撲條件下, 多枚導彈采用領從制導體制協同攔截機動目標的時變編隊制導問題, 通過控制從彈跟蹤期望的時變編隊, 實現了多導彈對機動目標的協同攔截。 文獻[18]針對三維場景下, 多枚弱機動導彈協同攔截強機動目標的問題, 通過將導彈的可達區域在二維空間下表示, 提出一種基于協同覆蓋策略的協同制導律, 實現了多枚弱機動導彈在加速度受限情況下, 對強機動目標的協同攔截, 該方法具有較強的工程實用性。
基于上述討論, 為了處理導彈軸向不可控情況下, 多導彈協同攔截機動目標的協同制導問題, 分別采用在線和離線設計剩余飛行時間的思想, 設計了分布式時間協同制導律和指定攻擊時間制導律, 從而實現了對機動目標的同時或依次攻擊。
1 制導模型及剩余飛行時間計算
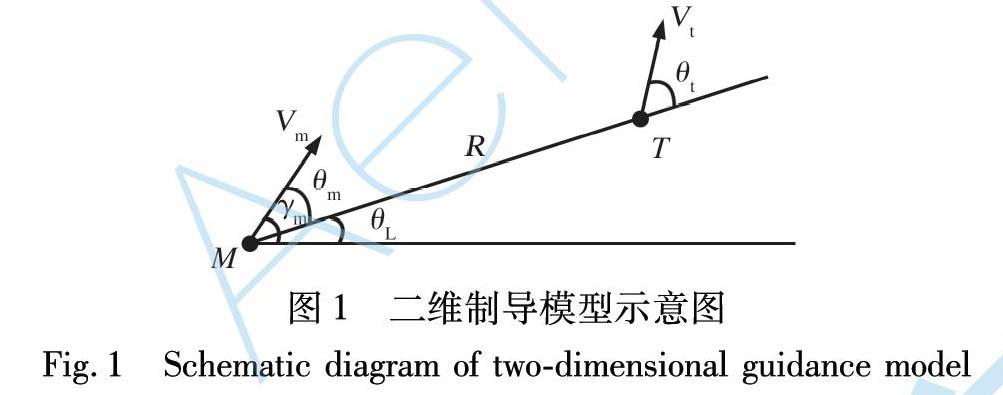
首先給出導彈和目標在二維平面內的制導模型示意圖, 如圖1所示。
圖中, M和T分別表示導彈和目標; R表示導彈和目標之間的相對距離; Vm和Vt分別為導彈和目標的速度; θm和θt為導彈和目標的前置角; θL表示視線角。 則制導模型的動力學方程可以表述為
R·=Vtcosθt-Vmcosθm=Vr(1)
Rθ·L=Vtsinθt-Vmsinθm=Vθ(2)
θ·m=amVm-θ·L(3)
θ·t=atVt-θ·L(4)
對導彈剩余飛行時間(time-to-go,? tgo)的估算是針對機動目標實現協同攻擊的前提, 對剩余飛行時間的研究不僅需要研究如何更準確地估算出導彈的攻擊時間, 還要兼顧考慮其動力學模型是否可控。 現階段, 針對打擊機動目標的剩余飛行時間, 由于目標機動的未知性, 尚無有效精確的數學解析式, 大多采用通過一些假設來求得近似的剩余飛行時間。 因此, 給出以下三種常用的剩余飛行時間的表達式, 并對其特性進行分析。
(1)基于比例導引的剩余飛行時間tgo1
若導彈M采用比例制導律, 則根據文獻[3], 可較精確地估計得到導彈M的tgo1為
tgo1=RVm1+θ2m2(2N-1)(5)
式中: N為導航系數, 滿足2<N<6。
tgo1在推導過程中用到了目標靜止和前置角為小量的假設條件, 實質上是導彈航向誤差的函數。 通常認為該形式的剩余飛行時間針對靜止目標有效; 而針對機動目標, 該形式的剩余飛行時間則會因目標運動存在一定的估計誤差。 因此, 針對機動目標, tgo1通常不能用來直接控制具體的剩余飛行時間。
(2) 瞬時剩余飛行時間tgo2
瞬時剩余飛行時間的定義為
tgo2=RVc(6)
式中: Vc為導彈和目標在視線方向上的接近速度。
tgo2定義為當前時刻導彈距目標的距離除以當前時刻導彈和目標的接近速度。 其物理定義簡單, 被廣泛應用于對導彈的剩余飛行時間的計算中。 然而該形式的剩余飛行時間未考慮導彈和目標的機動帶來的影響, 只能表征當前時刻下導彈和目標的瞬時剩余飛行時間。 在使用tgo2來調節導彈的飛行時間時, 由于其表達式分母為導彈和目標的接近速度, 對于具有較大初始誤差的情形, 導彈需要進行較大的機動來調整飛行軌跡, 進而消除飛行時間誤差, 這可能會引起導彈和目標接近速度符號的改變, 進而造成奇異問題。 因此, 對于多導彈協同制導而言, 該形式的剩余飛行時間通常適用于彈群初始tgo2相差不大的情形。
(3) 基于常值前置角的剩余飛行時間tgo3
文獻[14]從導彈和目標的相對運動學方程出發, 推導了在目標機動為0、 導彈前置角為常值下的剩余飛行時間的形式:
tgo3=R[Vr+2Vmcosθm-Vθtanθm]V2m-V2t(7)
在tgo3推導過程中, 要求運動目標的機動加速度為0且導彈前置角為常值, 其更像是針對運動目標攔截的一個特殊場景。 相比于tgo1, tgo3在推導過程中是直接基于導彈和運動目標的相對運動學方程, 沒有運用任何假設和近似條件; 相比于tgo2, tgo3不會發生奇異問題。 在針對機動目標的tgo估計中, 受目標機動影響, 雖然仍有一定的估計誤差, 但相比于tgo1和tgo2, 其估計精度更高且應用場景更廣。 因此, tgo3可以直接用來對導彈的剩余飛行時間進行設計。 這將在下一節協同制導律的設計中體現。
2 時間協同制導律設計
2.1 代數圖論
在多導彈協同制導的過程中, 導彈通過通信與相鄰的導彈交換狀態信息, 這種通信拓撲關系可以由圖論來表示。 在本文中, 多導彈之間的通信網絡由無向圖G=(v, ζ, C)來描述,? v表示圖G中所有節點組成的集合; ζ代表圖G中節點之間的連線; 矩陣C=[cij]∈Rn×n代表權系數矩陣, 若導彈i和導彈j之間能夠信息交換, 則有cij=1, 否則cij=0, 特別的cii=0, i∈{1, 2, …, n}。 若G是無向圖, 即若第i個導彈可以從第j個導彈獲得信息, 則第j個導彈也可以從第i個導彈獲得信息, 則有cij=cji。 如果無向圖中任意兩個節點都可以通過連線找到一條線路連接, 則稱無向圖為連通的。 定義圖G(C)對應的拉普拉斯矩陣為L=[lij]∈Rn×n, 其中矩陣元素為
lij=∑nm=1, m≠icim,? j=i-cij,? j≠i (8)
當多導彈之間的通信拓撲是無向且連通時, 則有下述假設和引理成立。
引理1[19]: 對于拉普拉斯矩陣L, 0是一個特征值, 并且滿足所有非零特征值都是正數, 所有項為1的列向量為其一個特征向量。
引理2[20]: 對任意的x∈Rn, 如果滿足1Tx=0, 則有xTLx≥λ2(L)xTx成立, 其中, λ2(L)表示矩陣L的最小非零特征值。
引理3[21]: 考慮非線性系統x·=f(x, t), x∈Rn, 假設存在一個連續正定、 徑向無界的函數V(x), 并且滿足
V·(x)≤-μV(x)-λVα(x)(9)
式中: μ, λ>0以及0<α<1是常數, 則原點是該非線性系統全局有限時間穩定的平衡點。 x(t0)=x0, t0是初始時間, 那么系統狀態到達平衡點的時間T滿足
T≤1μ(1-α)lnμV1-α(x0)+λλ(10)
引理4[22]: 考慮非線性系統x·=f(x, t), x∈Rn, 假設存在一個連續正定、 徑向無界的函數V(x), ε∈(0, 1), c>0, 0<δ<∞, 使得
V·≤-cVε+δ(11)
則系統是實際有限時間收斂的。
2.2 基于比例加時間偏置項的分布式協同制導律
比例導引形式簡單, 在工程中應用廣泛。 在對比例導引的分析中發現, 比例導引的導航系數直接影響著導彈的飛行彈道。 因此, 可以通過改變比例導引的導航系數來改變導彈的攻擊軌跡, 進而改變導彈的攻擊時間。 文獻[3]中針對靜止目標, 設計了具有時變導航比的協同比例導引, 通過改變導航比來實現攻擊時間的協同, 但該方法不能保證tgo的收斂時間。 文獻[13]針對靜止和機動目標, 通過在線改變導航系數, 分別設計了集中式和分布式的偏置比例導引, 但缺乏嚴謹的理論證明。 受文獻[23]的啟發, 針對tgo1的表達形式, 基于有限時間引理, 設計協同比例制導律如下:
ami=N-iVmiθ·LiN-i=Ni{1-k1isgn(ξi)-k2iξi}ξi=∑nj=1cij(tgoj-tgoi)(12)
證明: 首先將式(12)重新整理為
ami=N-i[1-k1isgn(ξi)-k2iξi]Vmiθ·Li(13)
對tgo1進行求導, 將式(13)代入, 并利用小角度假設化簡, 即sinθm=θm, cosθm=1-12θ2m, θ4m≈0, 可得
t·goi=-1+θ2miN2N-1-θmiRi(2N-1)V2miN[1-
k1isgn(ξi)-k2iξi]Vmiθ·Li=-1+
Nθ2mi2N-1[k1isgn(ξi)+k2iξi](14)
構造如下形式的李雅普諾夫函數:
V1=12∑nj=1cij(tgoj-tgoi)2=12tTgoLtgo(15)
式中: tgo=[tgo1, tgo2, …, tgon]T; L=[lij]∈Rn×n為圖G(C)對應的拉普拉斯矩陣。
則一致性誤差ξi可重寫為
ξ=-Ltgo(16)
式中: ξ=[ξ1, ξ2, …, ξn]T。
由于導彈之間的通信拓撲圖是無向且連通的, 因而cij=cji, 可得
∑ni=1ξi=∑ni=1∑nj=1cij(tgoj-tgoi)=0(17)
對V1求導, 并將上式帶入可得
V·1=tTgoLt·go=-ξTt·go=
-∑ni=1ξi-1+Nθ2mi2N-1[k1isgn(ξi)+k2iξi]= ∑ni=1ξi-Nθ2miξi2N-1[k1isgn(ξi)+k2iξi]=
-N2N-1∑ni=1[θ2mi(k1iξi+k2iξ2i)](18)
由于θmi>0, 假設在tgoi收斂之前θmi≠0, 則存在常數ε0>0, 使得θmi>ε0。 令k1=min{k11, k12, …, k1n}, k2=min{k21, k22, …, k2n}, 則上式可重寫為
V·1=-N2N-1∑ni=1[θ2mi(k1iξi+k2iξ2i)]≤
-Nε202N-1k1∑ni=1ξi+k2∑ni=1ξ2i(19)
由引理1中拉普拉斯矩陣的性質可知L1=0, 因而有1TL1=(L121)T(L121)=0, 故L121=0。 進而有1TL12=0T, 故1TL12tgo=0。 由引理2和式(16)可知:
ξTξ=tTgoLLtgo=tTgoL12LL12tgo=
(L12tgo)TLL12tgo≥
[λ2(L)](L12tgo)TL12tgo≥[λ2(L)]tTgoLtgo≥2[λ2(L)]V1(20)
將式(20)代入式(19)中可得
V·1=-Nε202N-1[k1(ξTξ)12+k2ξTξ]≤
-[2λ2(L)]12k1Nε202N-1V121-2k2[λ2(L)]Nε202N-1V1(21)
由引理3可知, 各導彈的剩余飛行時間tgoi可以在有限時間內收斂到一致。 至此, 證明完成。
注1: 所設計的協同比例制導律實質是在傳統的比例制導律基礎上加上時間誤差偏置項組成, 其中ξi被稱為導彈剩余飛行時間的一致性誤差。 當ξi>0時, 表示第i枚導彈的剩余飛行時間小于與其具有通信交流的其他導彈的平均剩余飛行時間, 即表明該枚導彈剩余飛行時間較小, 需要增大其剩余飛行時間, 此時N-i會減小, 這表示導彈的飛行軌跡將更彎曲。 同樣地, 當ξi<0時, 表示第i枚導彈的剩余飛行時間較大, 需要減小其剩余飛行時間, 此時N-i會增大, 這表示導彈的飛行軌跡將更平直。 當ξi≈0時, 此時制導律變為傳統的比例導引, 從而保證對目標的有效打擊。 實際上, 在式(12)的制導律形式中, 并不需要導彈非常精確的剩余飛行時間, 因為并沒有通過tgo1去設計具體的攻擊時間, 而是將其作為協調變量, 通過協調變量的變化在線調整制導律參數, 實現協同攻擊。
注2: 上述制導律的推導是建立在導彈通信拓撲為無向且連通的情況下, 然而實際上, 對于有向圖的情形, 當彈群中的導彈僅能與相鄰的導彈進行單向通信時, 仍然滿足式(17)的條件, 即制導律仍然成立, 這點將在仿真中予以驗證。
2.3 基于非線性干擾觀測器的指定攻擊時間制導律
在針對諸如戰機等機動目標的協同攔截時, 目標可能會在導彈來襲前某段時刻進行機動來躲避攻擊, 若導彈總的末制導攻擊時間可以提前指定, 則更有利于針對該類機動目標的協同攔截。
若要對導彈的攻擊時間進行設計, 則需要用到導彈tgo的動力學模型。
基于tgo3進行制導律設計。 首先對tgo3進行求導并整理可得
t·go3=-1+V2θsec2θmV2m-V2t-RVθsec2θmVm(V2m-V2t)am-
Rsin(θm+θt)cosθm(V2m-V2t)at=F+Bam+D(22)
式中: F=-1+V2θsec2θmV2m-V2t; B=-RVθsec2θmVm(V2m-V2t);
D=
-Rsin(θm+θt)cosθm(V2m-V2t)at。
令期望的攻擊時間為Td, 則可定義滑模面(即攻擊時間誤差):
St=t+tgo3-Td(23)
對滑模面St求導可得
S·t=1+t·go3=1+F+Bam+D(24)
式中: D包含有目標的加速度和前置角等信息, 在實際作戰過程中, 包含目標運動信息的狀態通常不易被精確獲得, 這也就意味著式(22)中的D為未知量, 令x=tgo3+t, 則基于非線性擾動觀測器可設計制導律如下:
am=-F+1+D^+k1St+k2sgnγ(St)B
D^=ω+k0x
ω·=-k0ω-k0(1+F+Bam+k0x)(25)
式中: k1和k2為制導律中大于0的待設計的常數; k0為擾動觀測器中的待設計常數。
證明: 首先, 定義觀測器跟蹤誤差D~=D-D^, 假設系統擾動D·有界, 滿足D·≤β, 選擇李雅普諾夫函數V2:
V2=12S2t+12D~2(26)
對V2求導可得
V·2=StS·t+D~D~·=St(1+F+Bam+D)+D~D~·=St(-k1St-k2sgnγ(St)+D-D^)+D~D~·=-k1S2t-k2Stγ+1+StD~+D~D~·(27)
且
D~D~·=D~(D·-D^·)=D~(D·-ω·-k0x·) (28)
根據觀測器定義可知:
ω·+k0x·=-k0ω-k0(1+F+Bam+k0x)+
k0(1+F+Bam+D)=-k0ω-k0x2+k0D=
-k0(ω+k0x)+k0D=-k0D^+k0D=k0D~ (29)
將式(29)代入式(28)可得
D~D~·=D~(D·-D^·)=D~(D·-ω·-k0x·)=
D~(D·-k0D~)=-k0D~2+D~D·≤-k0D~2+12D~2+12β2≤-k0-12D~2+12β2(30)
進一步, 將式(30)代入式(27)可得
V·2=-k1S2t-k2Stγ+1+StD~+D~D~·≤
-k1S2t-k2Stγ+1+12S2t+12D~2-
k0-12D~2+12β2≤-k1-12S2t-
(k0-1)D~2+12β2≤-αV2+σ(31)
式中: α=min2k1-12, 2(k0-1); σ=12β2。
由式(31)和引理4可得, 系統是實際有限時間收斂的, 至此, 制導律式(25)穩定性得證。
雖然tgo3的推導仍是基于目標機動為0且導彈前置角為常值下得到的, 當目標機動時, 這無疑將會引入估計誤差, 但在稍后的仿真分析中可以看出, 式(25)仍然可以保證導彈以期望的攻擊時間攔截目標。
3 仿真分析
3.1 協同比例制導律仿真分析
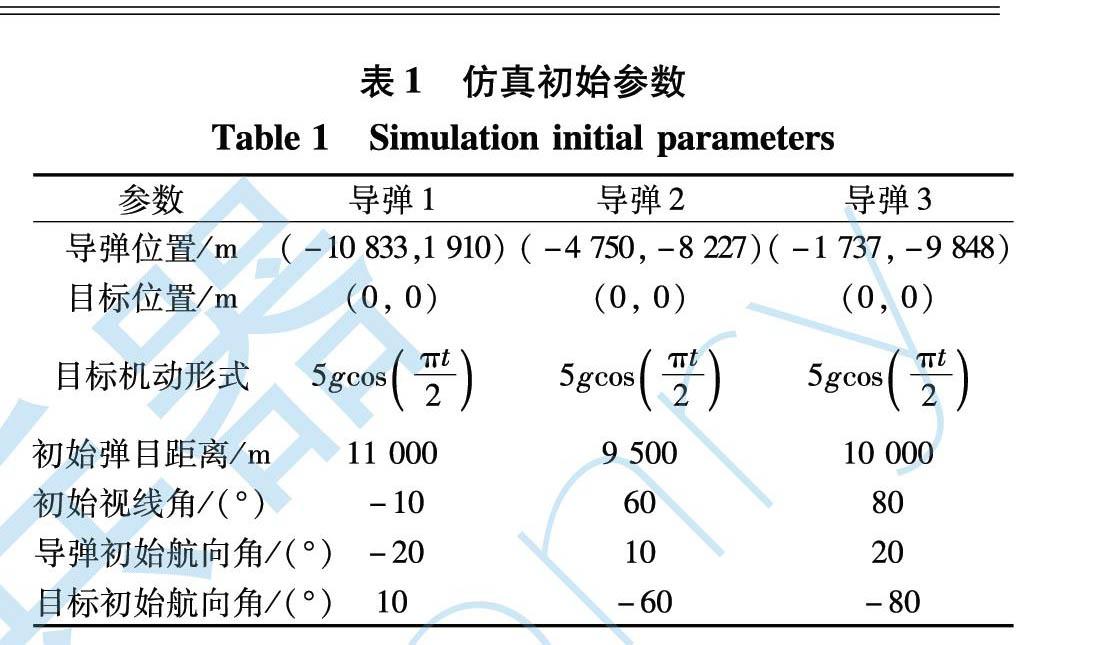
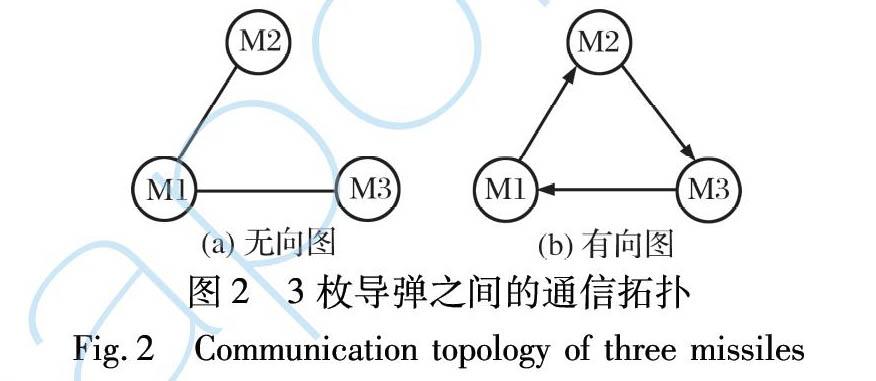
首先對所設計的基于比例加偏置項的時間協同制導律進行仿真驗證。 以3枚導彈攔截1個機動目標為例, 仿真初始參數設置如表1所示, 3枚導彈之間的通信網絡如圖2所示, 分別給出導彈通信拓撲為無向和有向的情形。 選擇目標以余弦機動at=5gcosπt2的情況進行仿真, 并以比例導引作為對比, 對所設計的制導律進行驗證。 導彈仿真初始參數為: Ni=3; k11=2.8; k12=2.5; k13=2.6; k21=k22=k23=1.2。 無向圖和有向圖的通信矩陣分別為: C無向=011100100; C有向=001100010。
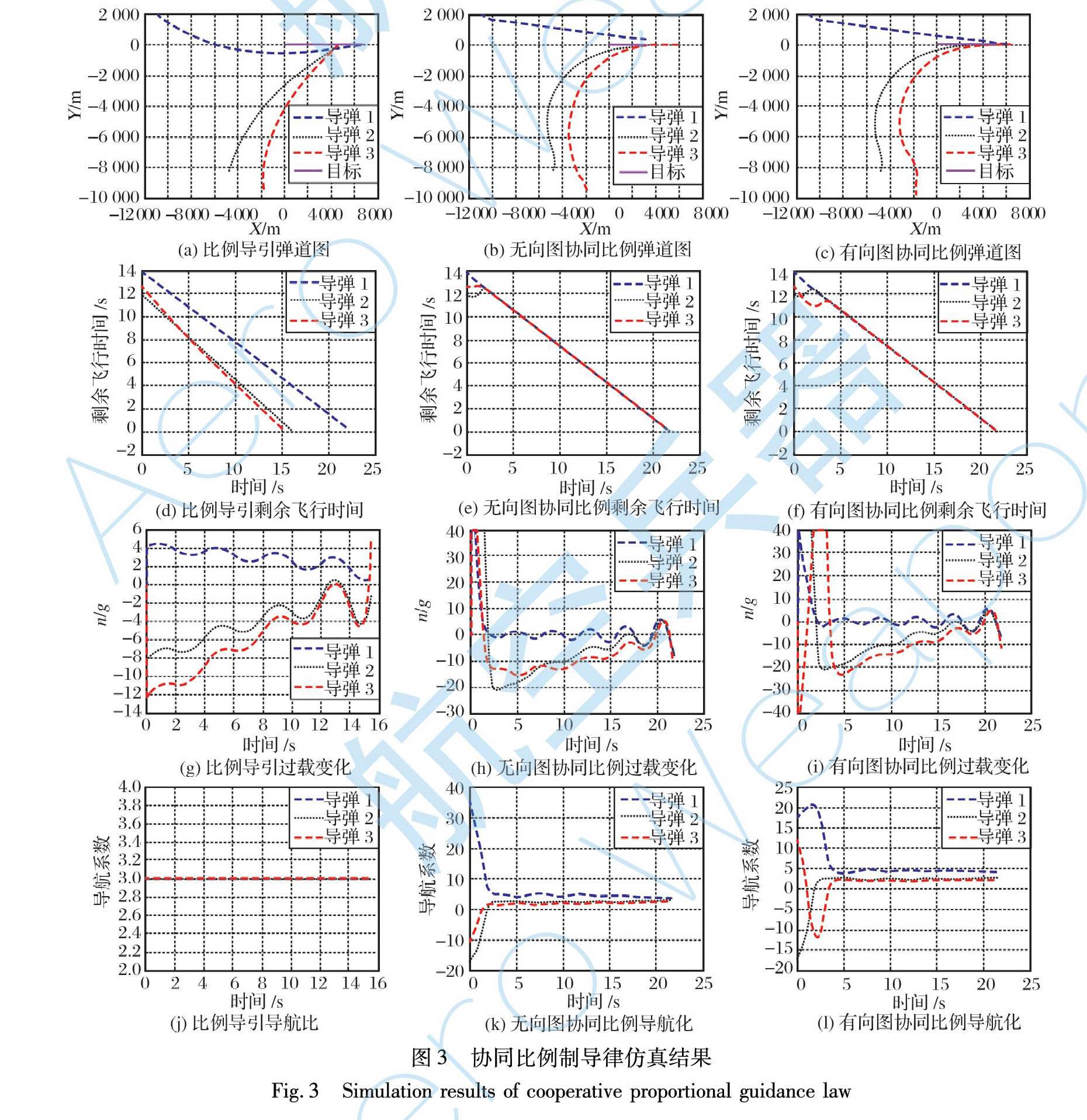
仿真結果如圖3所示。 其中脫靶量和制導時間如表2所示。
導彈31.2821.80圖3給出了所設計的協同比例制導律和傳統比例制導律之間的仿真對比。 圖3(a)~(c)為比例導引和在有向和無向圖下協同比例導引的彈目運動軌跡, 可知, 所設計的協同制導律可以保證3枚導彈同時命中目標。 圖3(d)~(f)為導彈剩余飛行時間的變化曲線, 可知, 協同比例制導律可以糾正較大的初始飛行時間誤差, 并保持較高的精度收斂。 圖3(g)~(i)為協同制導律中導彈過載的變化曲線, 可知, 相比比例導引, 協同制導律在初始階段需要較大的加速度來調整攻擊時間誤差。 圖3(j)~(l)為協同制導律的導航系數的變化曲線, 可知, 不同的通信拓撲下, 導彈的導航系數變化趨勢不同, 但最后隨著剩余飛行時間的收斂, 導航系數也將收斂。
注3: 協同比例制導律的核心是調整比例導引的導航系數, 進而調整各導彈的攻擊彈道, 實現協同攻擊。 仿真結果證明所設計的協同制導律對于機動目標仍能以較高的精度實現協同打擊。 雖然在協同比例制導律中采用的tgo1是基于靜止目標假設推導出來的, 但在制導律的設計過程中, 并沒有用tgo1來控制導彈實際的飛行時間, 而是將目標在每個時刻視為靜止的點, 將每枚導彈的剩余飛行時間視為協調變量, 來動態調節各自的導航比。 隨著導彈與目標相對距離的減小, tgo1的估計誤差也越來越小, 從而實現對機動目標的協同打擊。
3.2 指定攻擊時間制導律仿真分析
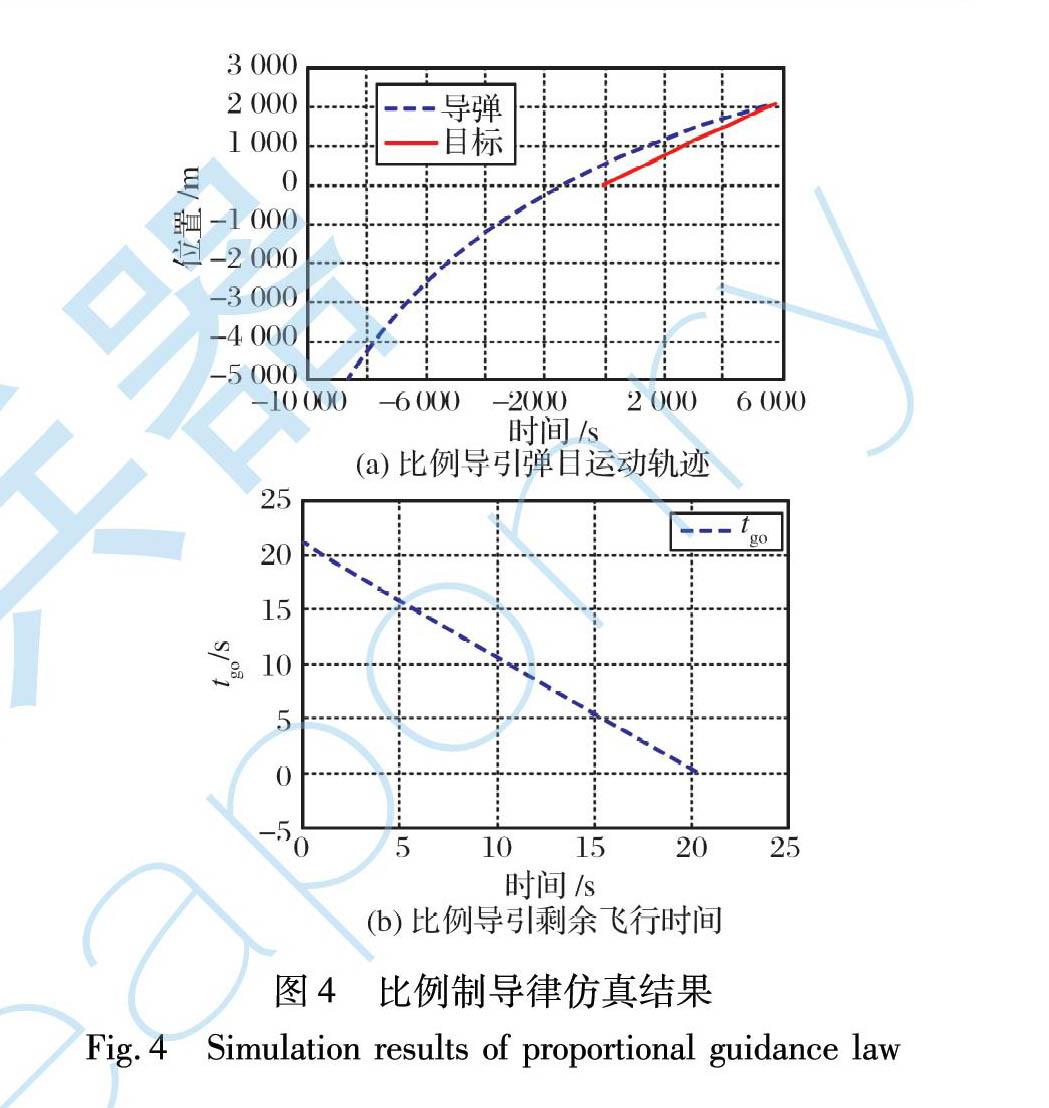
對基于tgo3所設計的指定攻擊時間協同制導律進行仿真分析。 以單枚導彈攻擊機動目標場景為例, 導彈的仿真初始條件如表3所示。 在傳統比例制導律下的仿真結果如圖4所示。
由圖4可以看出, 在傳統比例制導律下, 導彈攻擊時間為20.46 s。 為了驗證所設計的指定攻擊時間制導律, 分別選擇Td=21 s, Td=22 s, Td=23 s三種場景進行仿真驗證。 仿真初始參數如下:
Td=21 s時, [k1, k2]=[1.7×10-6, 1.8×10-5]×R;
Td=22 s時, [k1, k2]=[2×10-6, 3.6×10-5]×R;
Td=23 s時, [k1, k2]=[3×10-6, 2.3×10-5]×R;
k0=10, γ=0.9。 仿真結果如表4所示。
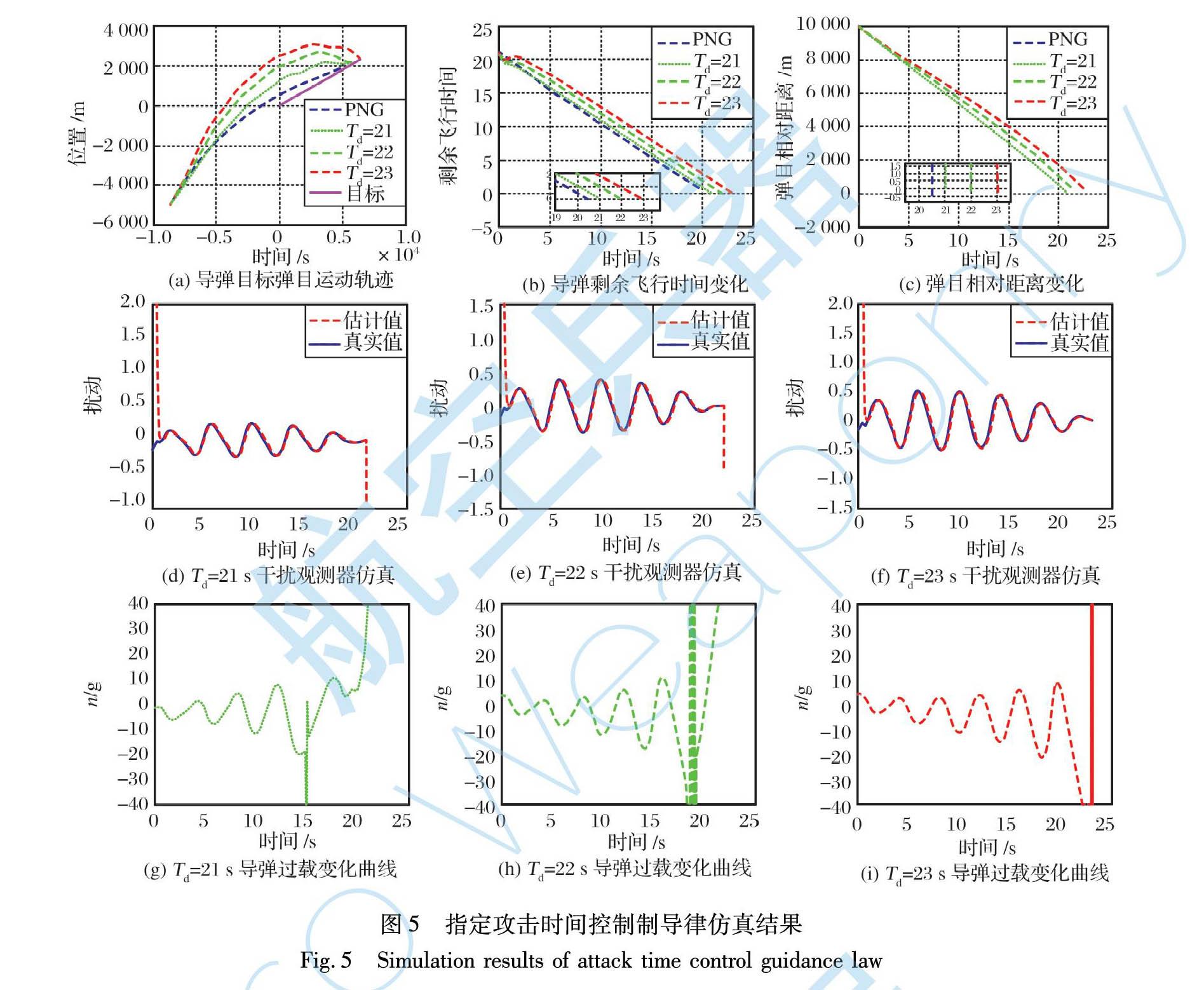
圖5給出了所設計的指定攻擊時間控制制導律的仿真結果。
由圖5可知, 所設計的制導律可以保證導彈以期望的攻擊時間攻擊目標。 圖5(c)為彈目相對距離的變化, 可以看出, 在不同的攻擊時間下, 導彈仍能以較高的精度打擊目標。 圖5(d)~(f)為不同的Td下, 所設計的擾動觀測器的估計結果, 可以看出, 所設計的觀測器可以較好地跟蹤系統擾動。 圖5(g)~(i)為導彈過載的變化曲線, 可以看出, 過載在末制導過程中會發生抖振, 這主要是因為本文所使用的tgo3未考慮目標的機動, 這無疑會引起tgo3的估計誤差, 進而在制導末期造成滑模面的抖振問題。
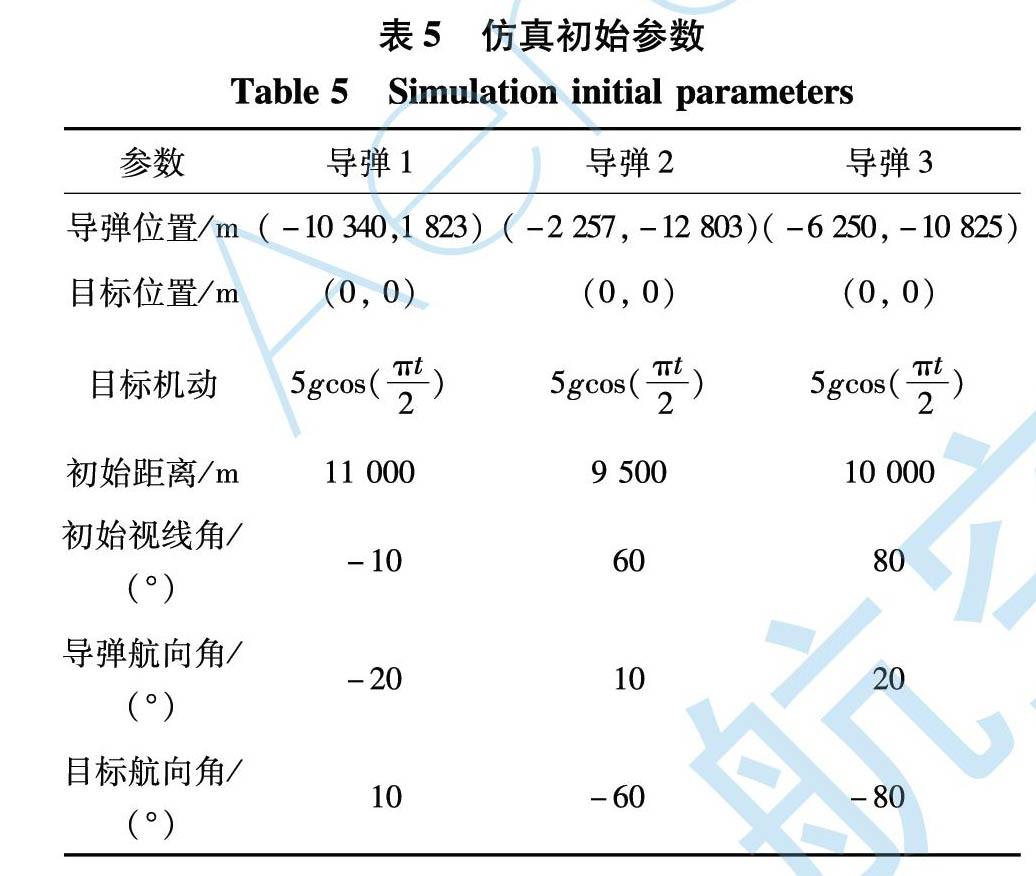
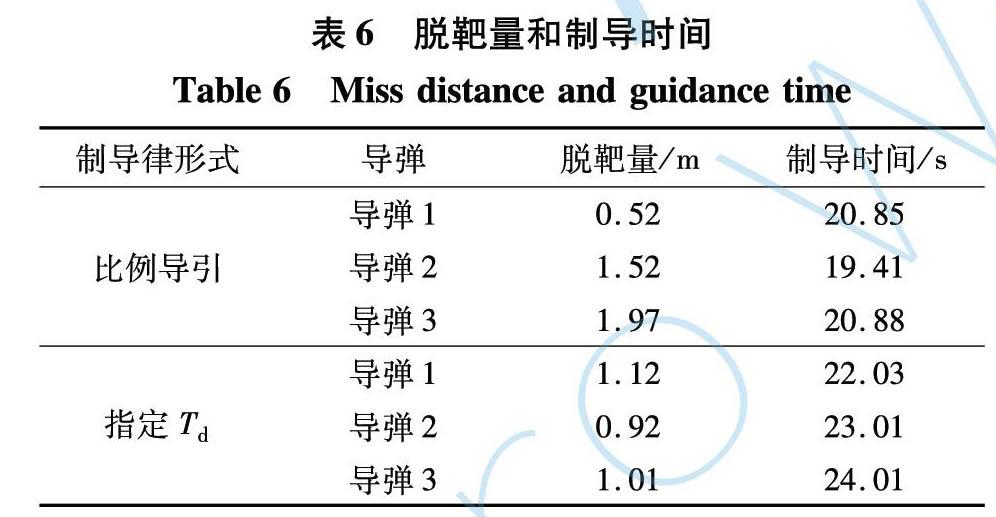
為進一步驗證所設計制導律的有效性, 考慮3枚導彈攻擊機動目標的場景。 仿真的初始參數如表5所示。 仿真結果如圖6所示, 脫靶量和制導時間如表6所示。
圖6給出了所設計的指定攻擊時間制導律協同攻擊某機動目標的仿真結果。 圖6(a)~(d)為導彈在比例導引和本文所設計的指定攻擊時間制導律下的彈道圖和彈目相對距離變化圖, 可以看出, 所設計的制導律可以保證各導彈以期望的攻擊時間依次打擊目標, 這在攻擊一些戰機等目標的場景中具有重要意義。 圖6(e)為指定攻擊時間制導律的剩余飛行時間變化曲線。 圖6(f)為3枚導彈的過載變化曲線。
注4: 與常規比例導引相比, 所設計的指定攻擊時間制導律彈道更加彎曲, 這是因為指定的攻擊時間較比例導引所需時間更長, 需要導彈進行額外的機動來調整攻擊時間。 雖然該制導律所采用的tgo3是基于目標不機動、 導彈前置角為常值下的條件推導的, 但是相比于tgo1, tgo3的推導是基于導彈和目標的相對運動學方程得到的, 且沒有用到任何近似條件。 當目標機動時, 將目標機動帶來的影響視為擾動, 以此來實現對導彈攻擊時間的控制。 需要注意的是, 由于tgo3估計誤差的存在, 在制導末期會造成滑模面的抖振問題。 下一步工作中, 將致力于解決導彈過載的抖振問題。
注5: 實質上, 本文所設計的兩種不同制導律, 其根本區別在于協同比例制導律是通過建立導彈的剩余飛行時間與導航系數之間的關系, 利用導航系數改變導彈彈道特性的特點, 通過網絡通信在線調整剩余飛行時間, 進而實現協同攻擊; 而指定攻擊時間制導律則主要是利用tgo3的動力學特性, 通過設計導彈加速度, 離線的改變導彈的剩余飛行時間, 從而實現對目標的同時或依次攻擊。 雖然兩種制導律的作用機理和制導體制不同, 但仿真分析證明, 這兩種制導律都能有效針對機動目標, 實現對機動目標的協同攻擊。
4 結? 論
本文針對多導彈協同攔截機動目標的問題, 從剩余飛行時間控制的角度出發, 通過對三種常用的剩余飛行時間形式的分析, 總結并梳理了不同剩余飛行時間形式的局限性和優越點。 分別基于在線調整導航系數和離線設計剩余飛行時間的思想設計了分布式協同比例制導律和具有指定攻擊時間控制的滑模制導律, 并給出嚴謹的理論證明與仿真分析。 通過與傳統的比例導引進行對比, 驗證了本文所設計的制導律的有效性。 在下一階段, 本文將針對具有較大初始偏差下, 綜合考慮導彈的視場角約束、 攻擊角約束及過載約束等條件, 設計多約束條件下的協同制導律。
參考文獻:
[1] Jeon I S,? Lee J I,? Tahk M J. Impact-Time-Control Guidance Law for Anti-Ship Missiles[J]. IEEE Transactions on Control Systems Technology,? 2006,? 14(2): 260-266.
[2] Lee J I,? Jeon I S,? Tahk M J. Guidance Law to Control Impact Time and Angle[J]. IEEE Transactions on Aerospace and Electronic Systems,? 2007,? 43(1): 301-310.
[3] Jeon I S,? Lee J I,? Tahk M J. Homing Guidance Law for Cooperative Attack of Multiple Missiles[J]. Journal of Guidance,? Control,? and Dynamics,? 2010,? 33(1): 275-280.
[4] Cho D,? Kim H J,? Tahk M J. Nonsingular Sliding Mode Guidance for Impact Time Control[J]. Journal of Guidance,? Control,? and Dynamics,? 2015,? 39(1): 61-68.
[5] Kumar S R,? Ghose D. Sliding Mode Control Based Guidance Law with Impact Time Constraints[C]∥American Control Conference,? 2013: 5760-5765.
[6] 洪超,? 夏群利,? 阮聰. 帶視場角約束的多彈三維協同制導律[J]. 戰術導彈技術,? 2020(6): 37-43.
Hong Chao,? Xia Qunli,? Ruan Cong. Multi-Missile Three-Dimensional Cooperative Guidance Law with Field-of-View Constraint[J]. Tactical Missile Technology,? 2020(6): 37-43.(in Chinese)
[7] 張振林,? 張科,? 郭正玉,? 等. 一種新型領從式多彈協同制導律設計[J]. 航空兵器,? 2020,? 27(5): 33-38.
Zhang Zhenlin,? Zhang Ke,? Guo Zhengyu,? et al. Design of a New Guidance Law for Guided Multiple Missiles[J]. Aero Weaponry,? 2020,? 27(5): 33-38.(in Chinese)
[8] Sinha A,? Kumar S R. Supertwisting Control-Based Cooperative Salvo Guidance Using Leader-Follower Approach[J]. IEEE Transactions on Aerospace and Electronic Systems,? 2020,? 56(5): 3556-3565.
[9] 花文濤,? 劉沛文,? 賈曉洪,? 等. 一種多彈協同制導策略[J]. 兵器裝備工程學報,? 2021,? 42(2): 180-183.
Hua Wentao,? Liu Peiwen,? Jia Xiaohong,? et al. Multi-Missile Co-operative Attacking Strategy[J]. Journal of Ordnance Equipment Engineering,? 2021,? 42(2): 180-183.(in Chinese)
[10] Yu J L,? Dong X W,? Li Q D,? et al. Cooperative Guidance Strategy for Multiple Hypersonic Gliding Vehicles System[J]. Chinese Journal of Aeronautics,? 2020,? 33(3): 990-1005.
[11] 鐘澤南,? 趙恩嬌,? 趙新華,? 等. 基于固定時間收斂的攻擊時間控制協同制導律[J]. 戰術導彈技術,? 2020(6): 30-36.
Zhong Zenan,? Zhao Enjiao,? Zhao Xinhua,? et al. Impact Time Control Cooperative Guidance Law Based on Fixed-Time Convergent[J]. Tactical Missile Technology,? 2020(6): 30-36.(in Chinese)
[12] 花文華,? 張擁軍,? 張金鵬,? 等. 多導彈攻擊時間協同的滑模制導律[J]. 中國慣性技術學報,? 2018,? 26(1): 98-102.
Hua Wenhua,? Zhang Yongjun,? Zhang Jinpeng,? et al. Sliding-Mode Guidance Law for Attack Time Cooperation of Multi-Missiles[J]. Journal of Chinese Inertial Technology,? 2018,? 26(1): 98-102.(in Chinese)
[13] Zhao J,? Zhou R. Unified Approach to Cooperative Guidance Laws Against Stationary and Maneuvering Targets[J]. Nonlinear Dynamics,? 2015,? 81(4): 1635-1647.
[14] Kumar S R,? Mukherjee D. Terminal Time-Constrained Nonlinear Interception Strategies Against Maneuvering Targets[J]. Journal of Guidance,? Control,? and Dynamics,? 2020,? 44(1): 200-209.
[15] 宋俊紅,? 宋申民,? 徐勝利. 一種攔截機動目標的多導彈協同制導律[J]. 宇航學報,? 2016,? 37(12): 1306-1314.
Song Junhong,? Song Shenmin,? Xu Shengli. A Cooperative Gui-dance Law for Multiple Missiles to Intercept Maneuvering Target[J]. Journal of Astronautics,? 2016,? 37(12): 1306-1314.(in Chinese)
[16] 郭正玉,? 王超磊,? 錢航,? 等. 帶有攻擊角約束的大機動目標協同攻擊制導律[J]. 西北工業大學學報,? 2020,? 38(6): 1257-1265.
Guo Zhengyu,? Wang Chaolei,? Qian Hang,? et al. Cooperative Intercepting Guidance Law for Large Maneuvering Target with Impact Angle Constraint[J]. Journal of Northwestern Polytechnical University,? 2020,? 38(6): 1257-1265.(in Chinese)
[17] Zhao Q L,? Dong X W,? Song X,? et al. Cooperative Time-Varying Formation Guidance for Leader-Following Missiles to Intercept a Maneuvering Target with Switching Topologies[J]. Nonlinear Dynamics,? 2019,? 95(1): 129-141.
[18] Chen Z Y,? Yu J L,? Dong X W,? et al. Three-Dimensional Coopera-tive Guidance Strategy and Guidance Law for Intercepting Highly Maneuvering Target[J]. Chinese Journal of Aeronautics,? 2021,? 34(5): 485-495.
[19] Ren W,? Beard R W,? Atkins E M. Information Consensus in Mult-ivehicle Cooperative Control[J]. IEEE Control Systems Magazine,? 2007,? 27(2): 71-82.
[20] Olfati-Saber R,? Murray R M. Consensus Problems in Networks of Agents with Switching Topology and Time-Delays[J]. IEEE Transactions on Automatic Control,? 2004,? 49(9): 1520-1533.
[21] Yu S H,? Yu X H,? Stonier R. Continuous Finite-Time Control for Robotic Manipulators with Terminal Sliding Modes[C]∥ Proceedings of the Sixth International Conference of Information Fusion,? 2003: 1433-1440.
[22] Zhu Z,? Xia Y Q,? Fu M Y. Attitude Stabilization of Rigid Spacecraft with Finite-Time Convergence[J]. International Journal of Robust and Nonlinear Control,? 2011,? 21(6): 686-702.
[23] Zhou J L,? Yang J Y. Distributed Guidance Law Design for Coopera-tive Simultaneous Attacks with Multiple Missiles[J]. Journal of Guidance,? Control,? and Dynamics,? 2016,? 39(10): 2436-2445.
Multi-Missile Cooperative Guidance Law for
Intercepting Maneuvering Target
Ma Mengchen,? Song Shenmin*
(Center for Control Theory and Guidance Technology,? Harbin Institute of Technology, Harbin 150001, China)
Abstract: Aiming at the problem of multi-missile cooperative interception of maneuvering targets,? two different cooperative guidance laws are designed based on the time-to-go. For the scenario of multi-missile distributed communication, a distributed cooperative proportional guidance law with time-varying navigation coefficients is designed based on the idea of biased proportional guidance. For the scenario of specified attack time,? based on the form of time-to-go under constant lead angle,? a sliding mode guidance law with a specified attack time is designed by using sliding mode control and nonlinear disturbance observer. Simulation results show that the two guidance laws proposed in this paper can effectively carry out cooperative attack or sequential attack against maneuvering targets.
Key words:? maneuvering target; time-to-go; biased proportional navigation; nonlinear disturbance observer; sliding mode control; multi-missile cooperation; guidance law

