基于阻抗特性的動力電池系統電磁干擾仿真與測試

張 戟，呂相杰，呂 鈺

（同濟大學汽車學院，上海201804）

隨著電動汽車的迅猛發展，開發出可靠的動力電池系統尤為重要。動力電池系統內部高低電壓和大電流同時存在，電磁環境極其復雜，在開發研究前期，盡早發現并解決電池包與電動汽車上其他系統及整車間的電磁干擾問題，是各主機廠和科研院所面臨的重要問題。動力電池系統是電動汽車一個重要的高壓部件，在高頻復雜工況下產生的瞬變電壓和電流會影響電池內部及周圍環境的電磁場分布，進而改變其擴散效應、極化效應的正常進程，對端電壓端電流產生反作用，引起電磁干擾問題。

目前國內外對于汽車電磁兼容性的研究中，幾乎都將動力電池從電磁干擾源中排除，對動力電池系統內部的電磁干擾問題不予考慮。在極限運行工況下，電池系統作為供電單元，會隨之發生較劇烈的電流電壓波動，因此動力電池系統的電磁干擾問題需要進一步的研究。

關于電池包等效模型的研究中，大致可以將其分為三類：電化學模型、電氣模型和數學模型。電化學模型是基于電池三維結構、材料、尺寸及內部化學反應等相關參數以大量的非線性微分方程的形式進行構建的，主要用于研究電池內部的電化學反應機理，能夠更加準確地預測電池行為，但同時也需要大量的計算資源［1］。數學模型是基于電池包大量數據和經驗公式提取的數學符號模型，可以用于預測電池行為，但沒有實際的物理意義，在電池包的系統層面常常耗費電池管理系統中的大量時間和空間［2］。賈玉健等人于2011年提出，對于電動汽車電池，可以用等效電路的方式模擬其動態特性，采用電壓源、電阻、電容等元器件的串并聯，與電路結合能夠獲取其電氣特性［3］。其精度高于數學模型，且具有電氣特性；低于電化學模型，但電氣模型中使用的元器件適用范圍更廣。

對于電池的電氣模型，一般采用等效電路的表達方式。等效電路有兩種構建方式：一種通過充放電測試進行參數辨識的方式得到不同元器件的參數構建等效電路，該方法能夠將溫度影響納入到模型中；另一種通過阻抗分析儀等設備，獲取電池頻域上的阻抗特性，用不同的電子元器件對其進行阻抗匹配擬合，從而構建其等效電路。

對于電驅系統建模，IDIR N.提出分別考慮共模和差模部分的建模方法，差模部分按照電驅正常工作狀態搭建，共模部分則對寄生參數加以考慮。用PSPICE進行仿真，仿真結果與實測數據在時域和頻域進行了驗證［4］。同濟大學張戟團隊對電驅系統形成了較為全面的電驅系統預測方法，包括基于電機阻抗模型建立、逆變器電流環控制下的傳導干擾模型以及按照GB/T 18655-2008搭建的輻射干擾模型［5］。清華大學余紹峰提出采用統計電磁學的方法對燃料電池汽車的電驅系統電磁噪聲加以分析，分析結果表明，電磁噪聲在時域上近似呈現正態分布，且隨電機電壓增大而減小［6］。基于傳統最大轉矩電流比控制，KE L提出一種新型最大轉矩電流比控制方法，既考慮了電機參數值的影響，又考慮了電機參數對d-q軸電流導數的影響，能夠實現電機在不同工況下的精確控制，同時減少傳統最大轉矩電流法的計算量［7］。李長紅基于公式法最大轉矩電流比控制，提出了將d-q軸電流與轉矩關系進行線性化處理的工程近似方法，能夠提高電機控制速度，減少占用內存，提高響應速度［8］。

由上述研究現狀可知，目前的研究大多將電機及逆變器本體與電機控制部分分開考慮，即大多數關于電磁兼容問題的研究中不考慮控制器部分對逆變器信號的影響。本文認為電磁兼容問題大多來源于開關器件的瞬變，而開關器件是受控制器激發而導通或關閉的，因此本文將二者結合，基于電動汽車正常運行工況，建立包括電驅系統在內的整個動力電池系統受控制器激發下的EMI（Electromagnetic Interference）電磁模型，盡量使仿真結果貼合實際。

1 動力電池系統全頻段阻抗特性

由于動力電池內部的化學反應及電磁特性并不能直觀地展現出來，因此對于電磁兼容方面的研究來說，電池包內部結構可看成黑箱。若給電池包輸入端一個擾動信號，那么輸出端就會得到一個信號輸出。

對一個穩定的線性系統M來說，如果輸入激勵信號為角頻率為ω的正弦波電信號（電壓或電流）X，則輸出信號也是一個角頻率ω的正弦波電信號（電壓或電流）Y。Y與X之間的關系如下：

式中：G為頻率響應函數，即傳遞函數。若X為電流信號；Y為電壓信號；則G為系統M的阻抗。

本文中所用動力電池單體為LG 60Ah Pouch Cell PE15版本，其正極材料為三元材料，負極為石墨材料。其額定容量為60Ah，標稱電壓為3.7V。

1.1 電池單體低頻（0.01～10kHz）阻抗特性研究

在阻抗定義中，若黑箱系統為穩定的電極系統，角頻率為ω的正弦波電流作為輸入信號，則此時電極系統的頻率響應函數，就是電化學阻抗。

1.1.1 低頻阻抗參數提取

低頻阻抗參數提取試驗平臺如圖1所示。

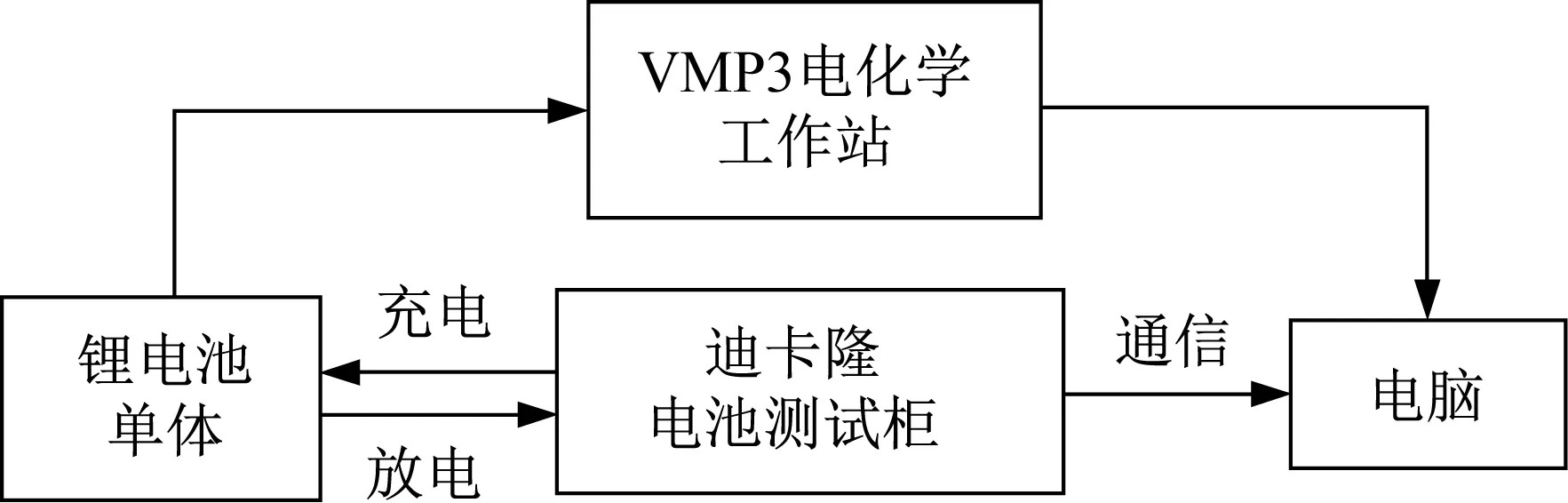
圖1 電化學阻抗譜測量設備Fig.1 Electrochemical impedance spectrum measuring equipment

LG鋰離子電池的電化學阻抗譜測量結果用奈奎斯特圖（Nyquist Plot）和波特圖（Bode Plot）進行表征，見圖2。

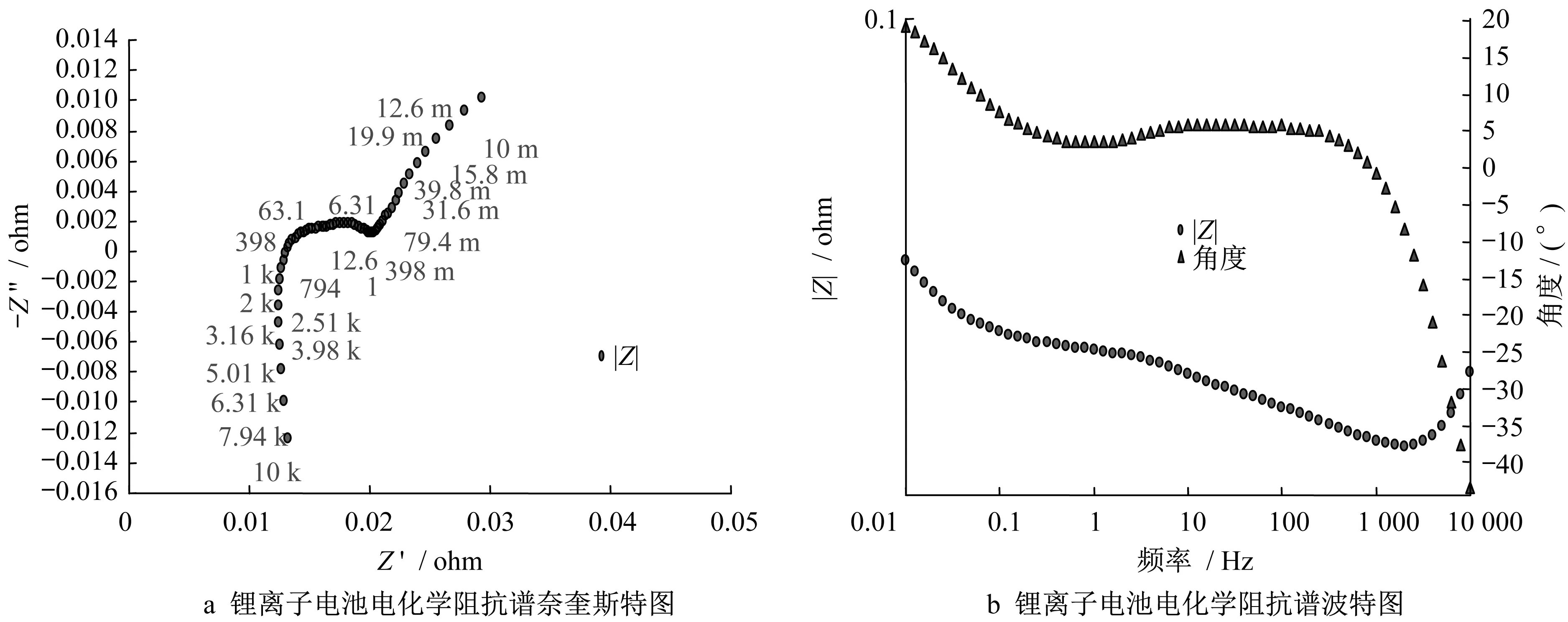
圖2 鋰離子電池電化學阻抗譜測量結果Fig.2 Measurement results of electrochemical impedance spectrum of lithium ion battery

其中，奈氏圖中的每個點代表不同的頻率，左側的頻率高，右側的頻率低。波特圖包括兩條曲線，橫坐標為頻率的對數坐標，縱坐標分別為阻抗的模值和阻抗的相位角。

2.1.2 低頻阻抗模型分析

利用電化學阻抗譜研究一個電化學系統的基本思路就是將電化學系統看作是一個等效電路，根據圖2中不同頻率段的性能表現，可以使用如圖3所示的等效電路進行擬合。

圖3 鋰離子電池低頻的等效電路模型Fig.3 Equivalent circuit model of low frequency for lithium ion battery

通過電路仿真軟件Zsimpwin對該模型進行擬合驗證，擬合參數值如表1所示，擬合結果如圖4所示。擬合曲線誤差在±3%以內，擬合效果較好。

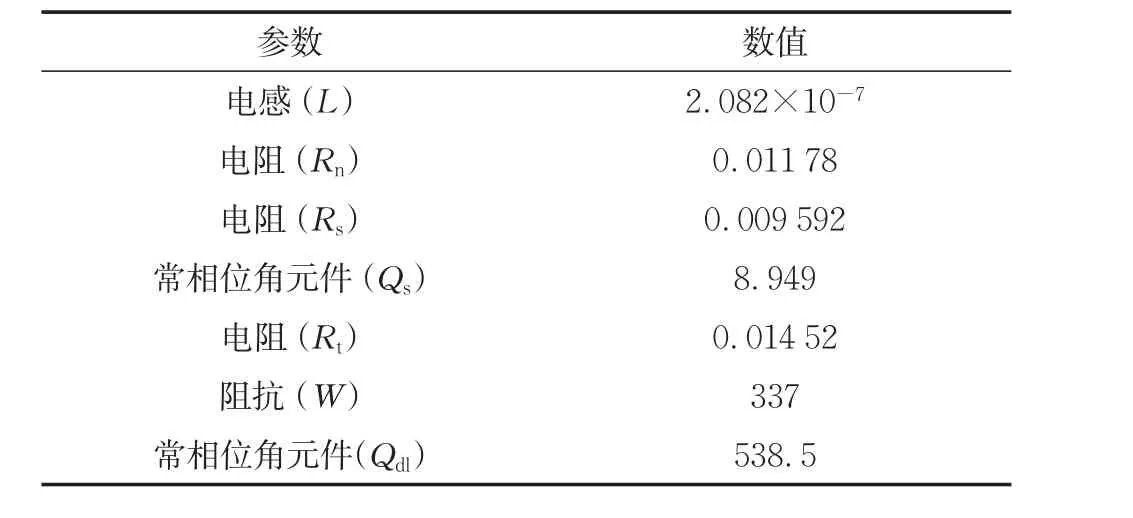
表1 鋰電池電化學阻抗擬合參數Tab.1 Electrochemical impedance fitting parameters of lithium battery

圖4 鋰離子電池電化學阻抗譜實測和擬合結果Fig.4 Measurement and fitting results of electrochemical impedance spectrum of lithium ion battery

1.2 電池單體中頻（10k～1MHz）阻抗特性研究

1.2.1 中頻阻抗參數提取

不同頻段下的測試原理不同，中頻段內的阻抗采用的測量方法為自平衡電橋法。本文采用日置IM3 570阻抗分析儀及配套夾具HIOKI9 262測量中頻段（10k～1MHz）阻抗。

搭建好整個測試平臺后，中頻阻抗特性測量結果如圖5所示。由圖可見，5個電池單體的阻抗特性基本保持一致。

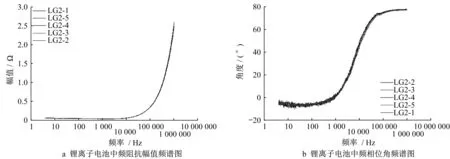
圖5 鋰離子電池中頻阻抗特性測量結果Fig.5 Measurement results of the intermediate frequency impedance characteristics of lithium ion batteries

1.2.2 中頻阻抗模型分析

該部分采用兩種建模方式：數學建模和等效電路。通過數學模型可以獲取等效電路的參數取值。

（1）數學模型

建立電池高頻數學模型根據實測電池阻抗，利用MATLAB進行數據擬合。

對于阻抗幅值-頻率特性，采用ployfit函數進行擬合，使所得到的函數值在擬合點處的值與原始點的坐標偏差最小。由于該部分的實測阻抗幅值在常規直線坐標系下呈現斜線形，因此用一階多項式對阻抗進行擬合，擬合效果如圖6a所示。而對于阻抗相位角-頻率特性，則采用Exponential指數函數進行擬合，擬合效果如圖6b所示。

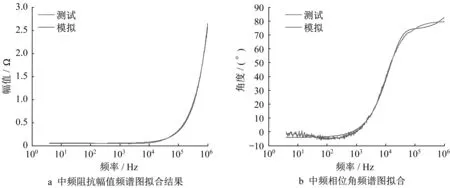
圖6 鋰離子電池中頻阻抗特性數學模型擬合結果Fig.6 Fitting results of the mathematical model of the lithium-ion battery’s intermediate frequency impedance characteristics

由圖可知兩者擬合效果較好，式（2）是其函數表達式。

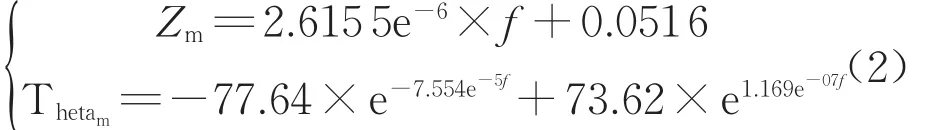
式中：f代表頻率；Zm表示阻抗；Thetam表示相位角。

（2）等效電路

在數學模型的基礎上，搭建電池單體中頻段的等效電路。由上面分析可知，電池單體的阻抗幅值與頻率關系呈現線性上升趨勢，數學表達式以式（2）表示。則在等效電路中可用電阻Rm和電感Lm的串聯表示，由于阻抗幅值較小，因此其值由式（3）近似可求，即

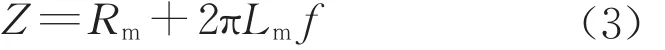
根據式（3）可得 Rm=0.051 6Ω，Lm=416nH。

在Multisim中搭建電池單體的等效電路，仿真阻抗與測試阻抗對比結果如圖7所示。

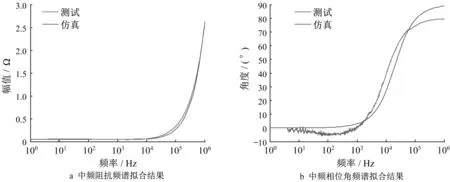
圖7 鋰離子電池中頻阻抗特性等效電路擬合結果Fig.7 Equivalent circuit fitting results of lithium-ion battery intermediate frequency impedance characteristics

由以上分析可知，在中頻段（10k～1MHz）范圍內，電池單體呈現由阻性到感性的變化。電感特性主要是由電子通過導線以及內部電極纏繞等產生的感抗行為引起的。該部分的等效電路基本與測試阻抗結果相吻合。

1.3 電池單體高頻（1M～108MHz）阻抗特性研究

目前國際國內通用的零部件電磁兼容標準規定的傳導測試頻率范圍上限為108MHz，因此本文根據標準規定的頻率范圍提取電池單體高頻（1～108MHz）阻抗參數。

1.3.1 高頻阻抗參數提取

高頻范圍內，網絡分析儀法的精確度較高。本文采用日置IM7 587及配套夾具IM9 200測量高頻阻抗特性。試驗平臺及試驗過程與中頻段測量保持一致。

同樣，搭建好整個測試平臺后，高頻阻抗特性測量結果如圖8所示。

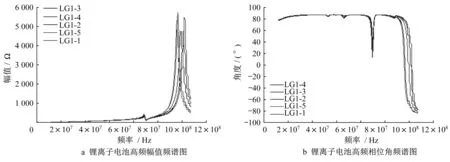
圖8 鋰離子電池高頻阻抗特性測量結果Fig.8 Measurement results of high-frequency impedance characteristics of lithium-ion batteries

由相角特性可以看出，鋰電池單體在100MHz附近相角由正值變為負值，表示其由感性變為容性。在高頻段鋰電池的電感、電容特性如圖9所示。

由圖9所示，不同鋰離子電池單體在高頻下的阻抗特性存在差異，因此選取5個電池單體的平均值進行后續仿真及分析。

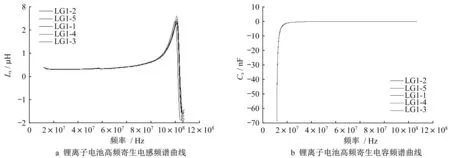
圖9 鋰電池單體的寄生電感和寄生電容頻譜曲線Fig.9 Spectral curves of the parasitic inductance and parasitic capacitance of a lithium battery cell

1.3.2 高頻阻抗模型分析

由圖8a電池單體的阻抗特性可以看出，高頻下電池存在兩個諧振點波峰，分別為72.2MHz對應幅值為397ohm和97.4MHz對應幅值為5 330ohm。因此考慮采用兩階LC并聯回路模擬其諧振點。

RLC并聯電路的阻抗為

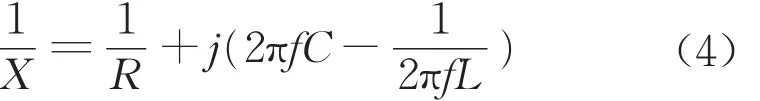
諧振頻率如下：

式中：X為復阻抗；R為電阻；L為電感；C為電容。如前所述，電池單體的諧振頻率分別為72.2MHz和97.4MHz，由式（5）可知

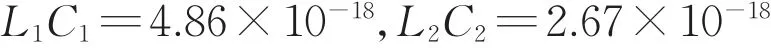
此外，由式（4）可知，在諧振點處阻抗為純電阻，與電感L1，L2和電容C1，C2無關。如前所述，諧振波峰值分別為397ohm和5 330ohm，因此為了便于后期計算擬合，可以假設R1=397Ω，R2=5330Ω。

為確定L1和L2的取值，可以分別取頻率為70和100MHz處的幅值代入計算，可得

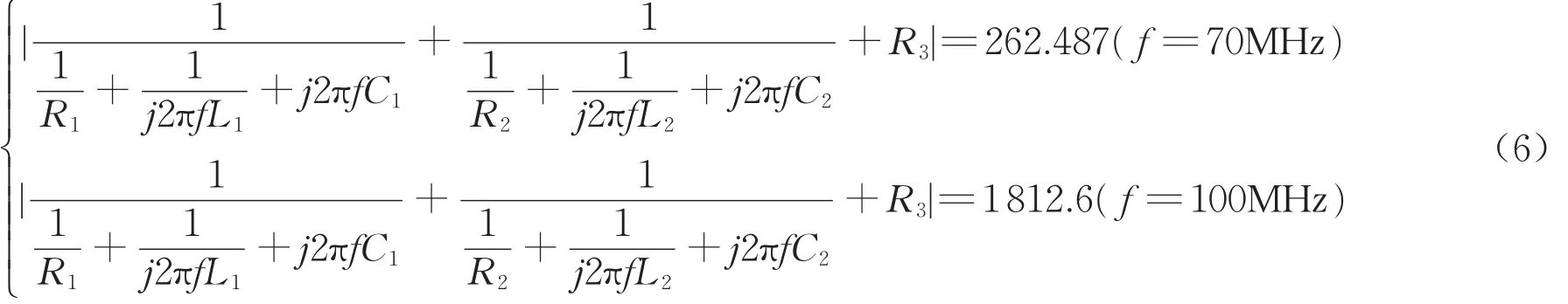
由 此 可 得 ，L1=0.01μH，L2=0.2μH，C1=486pF，C2=13.35pF。

采用Multisim軟件對阻抗進行擬合仿真，如圖10所示。綠色的探針用以監測電路電壓和電流，從而計算阻抗。采用AC仿真方式對1～108MHz進行掃頻仿真。

仿真與測試結果對比如圖11所示。

由圖11可知，鋰離子電池單體在高頻時從感性逐漸變為容性，在97.4MHz附近阻抗值達到最大值，電路擬合與測試結果基本一致，可以用于后續電路仿真。

將鋰離子電池單體的低頻、中頻和高頻數據組合在一起進行全頻段阻抗擬合仿真。以圖10的等效電路對全頻段阻抗特性進行擬合，擬合結果如圖12所示。

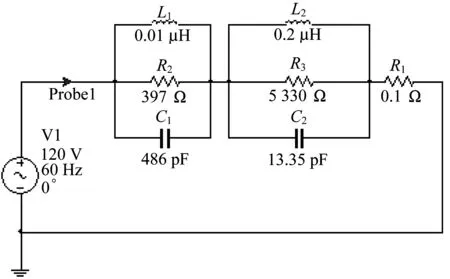
圖10 鋰離子電池高頻阻抗等效電路Fig.10 High-frequency impedance equivalent circuit of lithium-ion battery

由圖12可見，在全頻段內等效電路擬合的阻抗特性與測試結果較為一致。此外，本文所研究電池包電池單體之間通過低壓線束連接，而電池模組之間通過BUSBAR連接。考慮到BUSBAR通常會呈現一定的阻抗特性，影響電池包的電流及電壓分布，因此BUSBAR的阻抗也是電磁兼容性能研究中不可忽略的一部分。

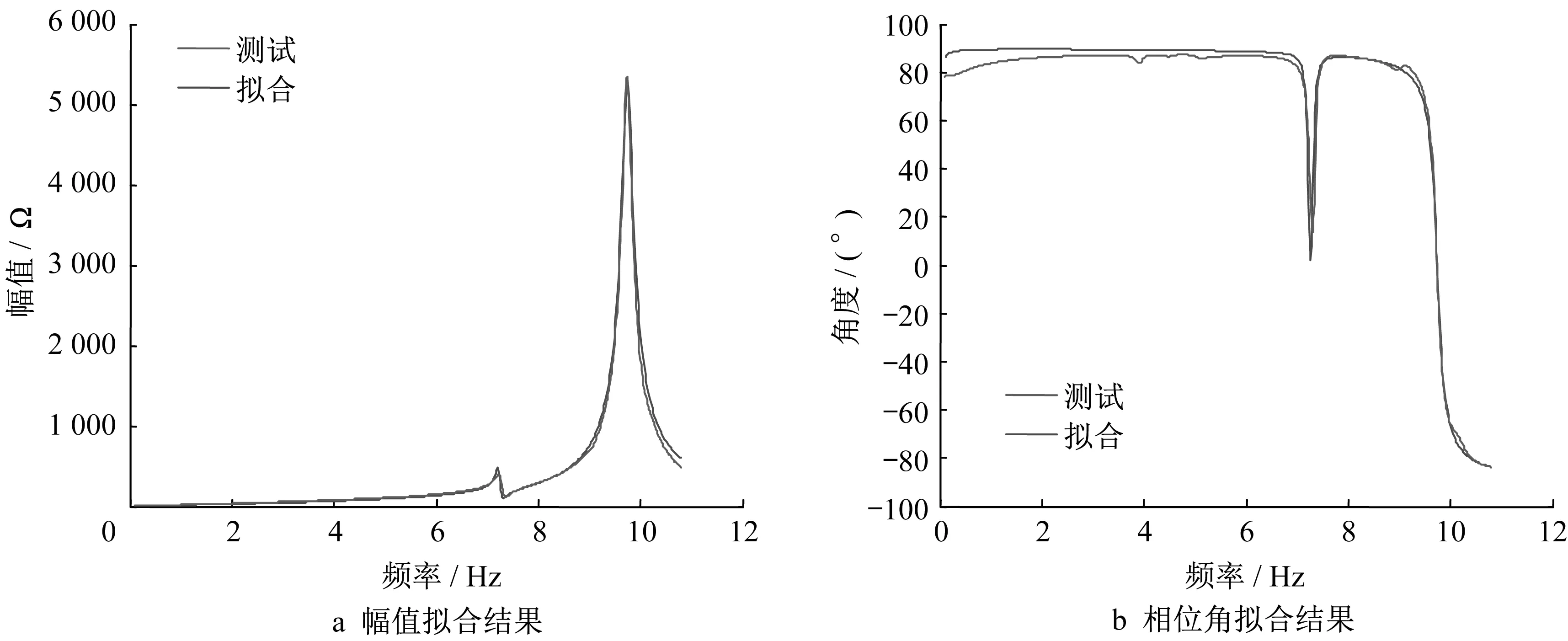
圖11 鋰離子電池高頻阻抗特性等效電路擬合結果Fig.11 Equivalent circuit fitting results of high-frequency impedance characteristics of lithium-ion batteries

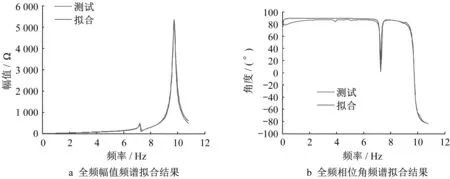
圖12 鋰離子電池全頻阻抗特性等效電路擬合結果Fig.12 Fitting result of equivalent circuit of full-frequency impedance characteristic of lithium ion battery

1.4 BUSBAR的阻抗特性研究

對于BUSBAR采用日置IM7587阻抗分析儀及其配套夾具IM9200測量其1～108MHz的阻抗特性，測試過程如圖13所示，阻抗特性的測量數據含有兩個波峰。產生波峰的頻率點分別為f=74.7MHz，Z=2 409.35Ω和f=82MHz，Z=1 855.03Ω。同樣采用1.3節的阻抗擬合方法對BUSBAR的阻抗特性進行等效電路擬合。最終確定等效電路的擬合參數如圖14所示。

圖13 BUSBAR高頻阻抗特性測試圖Fig.13 BUSBAR high frequency impedance characteristic test chart

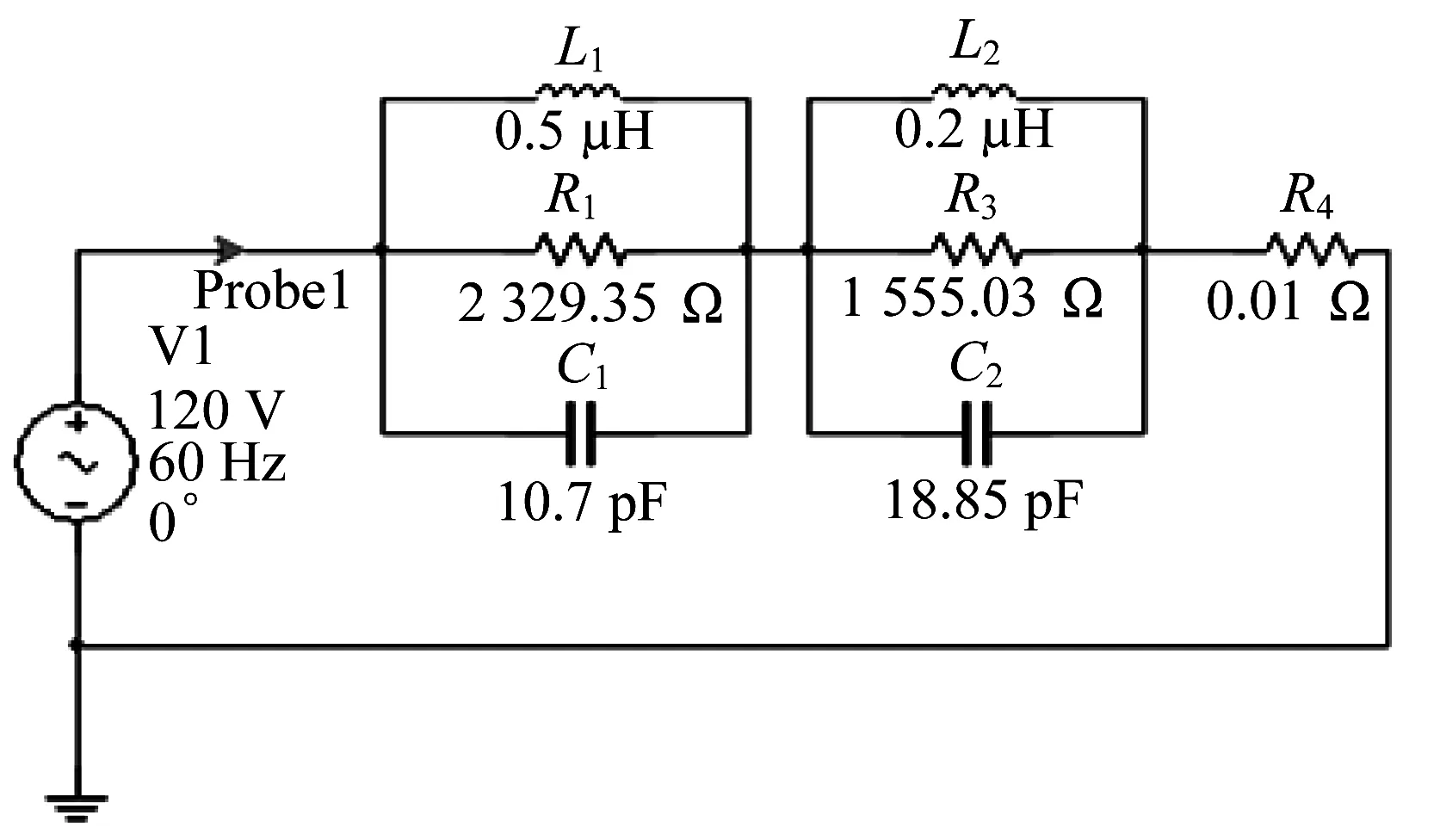
圖14 BUSBAR高頻阻抗等效電路Fig.14 BUSBAR high-frequency impedance equivalent circuit

將BUSBAR的阻抗特性仿真和實測結果進行對比，如圖15所示。可見其阻抗特性在幅值和相位角上存在一定誤差，但基本上呈現走向一致的趨勢。

2 電驅動控制系統建模

電驅系統作為動力電池系統EMI的主要干擾源，在不同控制方式下呈現出不同的電流及電壓變化情況。本文電驅系統為90kW永磁同步驅動系統，其仿真模型主要包含：空間矢量脈沖寬度調制（SVPWM）模塊、DC/AC逆變器、控制器算法等幾部分。

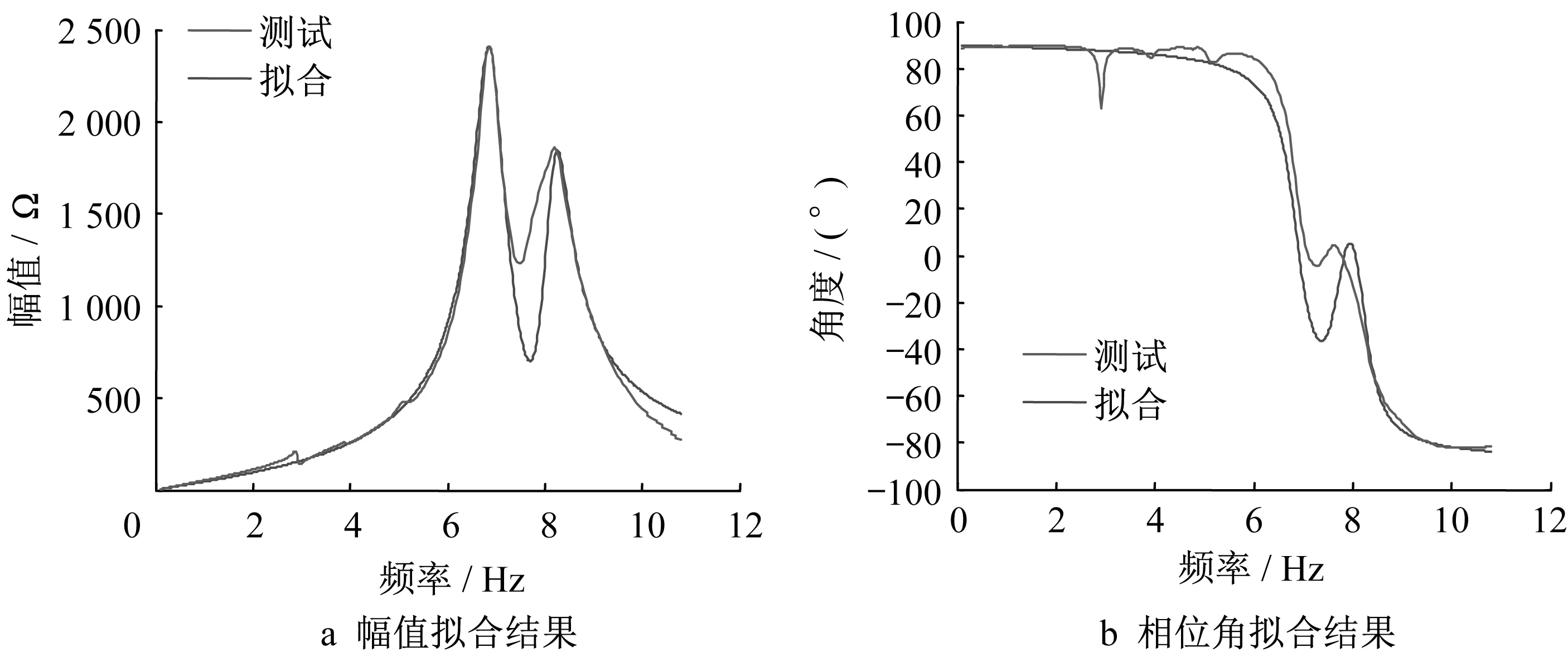
圖15 BUSBAR高頻阻抗特性等效電路擬合結果Fig.15 BUSBAR high-frequency impedance characteristic equivalent circuit fitting results

2.1 空間矢量脈沖寬度調制

對于三相三橋臂逆變器，每個橋臂有上下兩個開關管，開關管有兩種狀態：開啟和關閉，上下開關管的狀態相反。故三相三橋臂逆變器的開關狀態有23即8種，如圖16所示。

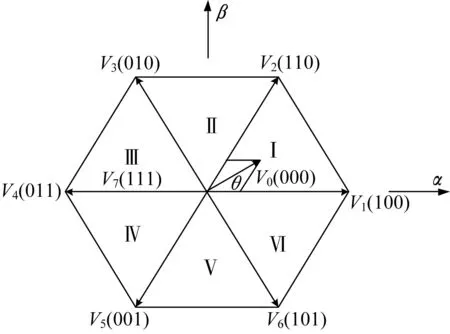
圖16 電壓空間矢量圖Fig.16 Voltage space vector

用Uα和Uβ表示合成矢量Uout在α、β軸上的分量，令

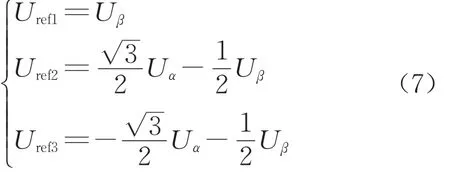
再定義3個變量A、B、C，通過分析可得若Uref1＞0，則A=1，否則A=0；若Uref2＞0，則B=1，否則B=0；若Uref3＞0，則C=1，否則C=0；令N=4C+2B+A，則可以得到N與扇區的關系，如表2所示。

表2 N與扇區的對應關系Tab.2 The correspondence between N and sectors

確定扇區矢量切換點，搭建的Simulink模塊如圖17所示。

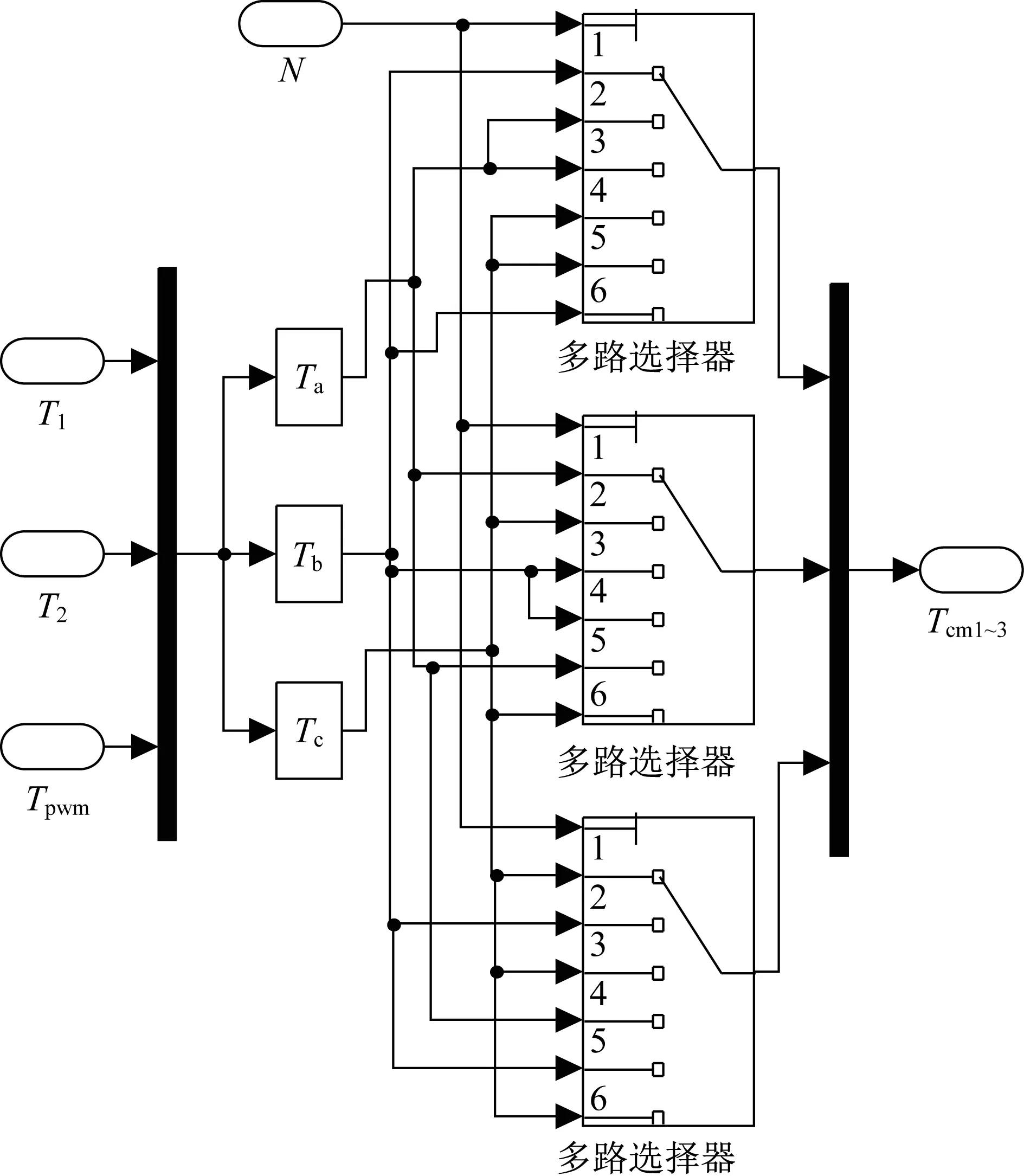
圖17 切換時間Tcm1，Tcm2和Tcm3的計算Fig.17 Calculation of switching timeTcm1，Tcm2and

使用三角波與所獲取的信號進行比較，Repeating Sequence模塊的頻率與PWM波的頻率保持一致為10kHz，幅值為周期的一半0.000 05，由此可以獲得逆變器使能端的六路信號，該模塊如圖18所示。在控制部分的采樣速率與IGBT的頻率保持一致，其他部分設置為后續仿真所需要的精度。因此使用RT模塊進行采樣速率控制，可以提高仿真速度。

圖18 產生PWM波Fig.18 Generate PWM wave

綜上所述，SVPWM部分的仿真模型如圖19 所示。

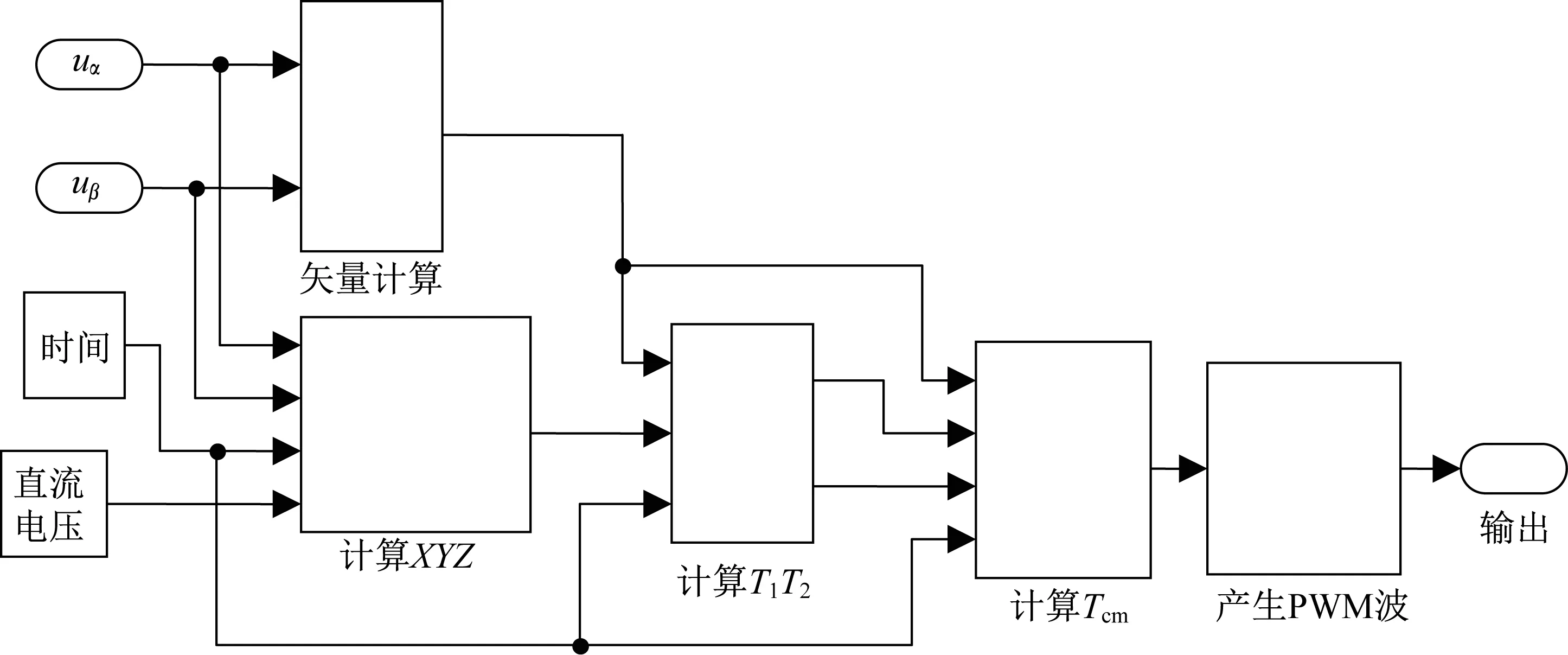
圖19 SVPWM波形產生模塊Fig.19 SVPWM waveform generation module

2.2 最大轉矩電流比控制

如前所述，凸極式永磁同步電機的電樞電流經過坐標變換后，電機的電磁轉矩表達如下：

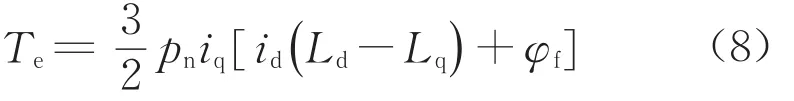
設Υ為電樞電流空間矢量與直軸位置的相位角，可得

則電磁轉矩為

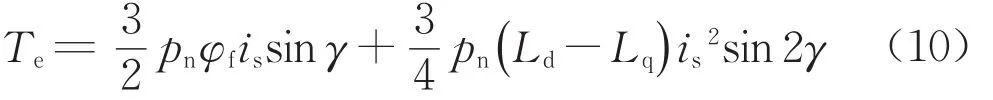
由此可得

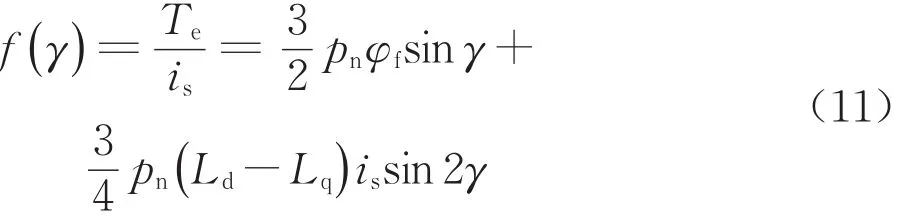
式中：Pn是電機極對數；Ld和Lq是電感分量；φf是磁鏈；id,iq為電流分量；is為定子電流矢量幅值。

電流is的幅值保持恒定，則單位電流電磁轉矩最大值時可得?f(γ)/?γ=0，進而可得

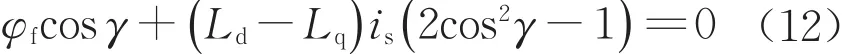
解得

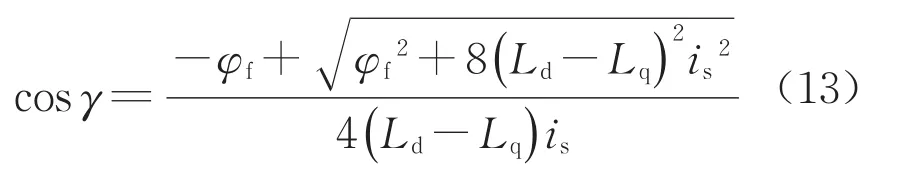
將式（12）代入式（8）可得

根據id和iq的關系，用iq表示id，得

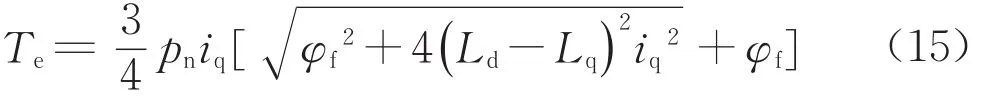
本文考慮采用查表法對該部分進行建模。電磁轉矩作為轉矩電流關系模塊的輸入，轉矩電流關系模塊的輸出作為id、iq的給定輸入，最后再經過電流調節器進而控制SVPWM模塊。

綜上所述，永磁同步電機的最大轉矩電流比控制框圖見圖20。

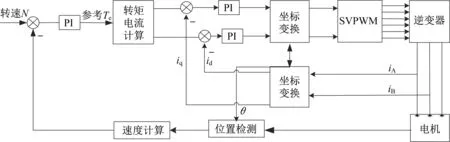
圖20 PMSM最大轉矩電流比控制原理Fig.20 PMSM maximum torque current ratio control principle

3 基于阻抗特性的動力電池系統EMI仿真與測試

3.1 工況模擬

依據GB/T 18387—2008中的工況設置，主要研究的工況為起步加速到70km·h-1以及從70km·h-1減速制動到停止的過程，后續的實車行駛測試都按照該工況進行。根據所需工況模擬電機轉矩和轉速，進行包括電池包在內的電驅系統控制仿真。

首先獲取汽車車速的運行狀態，如圖21所示。

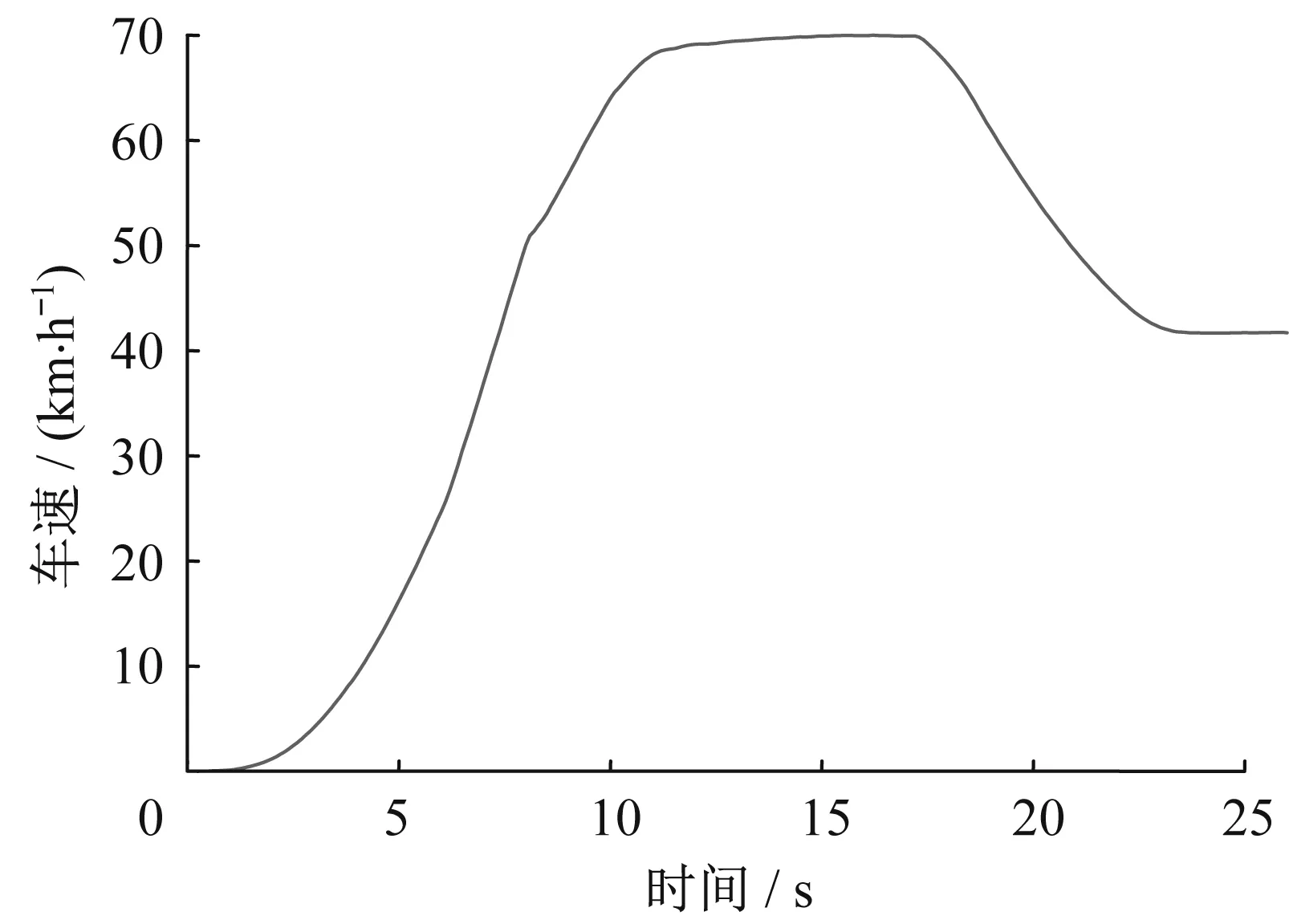
圖21 加減速工況下的車速隨時間變化Fig.21 Change of vehicle speed with time under acceleration and deceleration conditions

電動機的外特性如圖22所示，電動機的輸出轉矩為

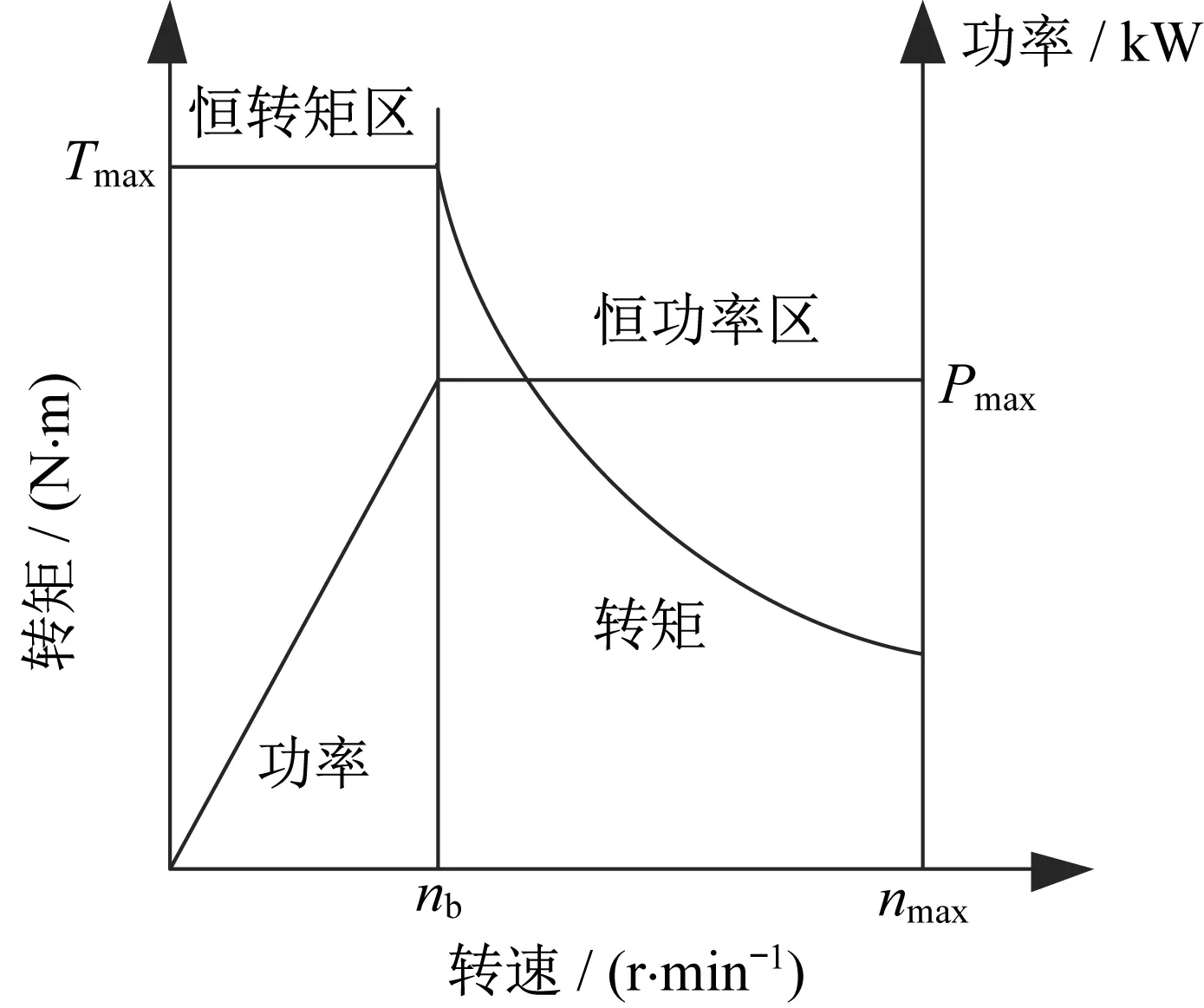
圖22 電動機的外特性曲線Fig.22 External characteristic curve of the motor

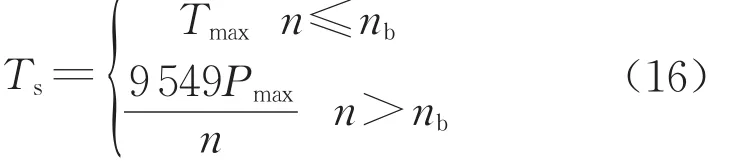
電動汽車的驅動力為

式中：Ts為電動機轉矩；it為傳動系總傳動比；ηt為傳動系統的機械效率；R為車輪半徑。在恒功率區域，電動汽車的驅動力是電機轉速的函數。滾動阻力Ff、Fw、Fj、空氣阻力和加速阻力的計算如下：

汽車行駛方程式如下：

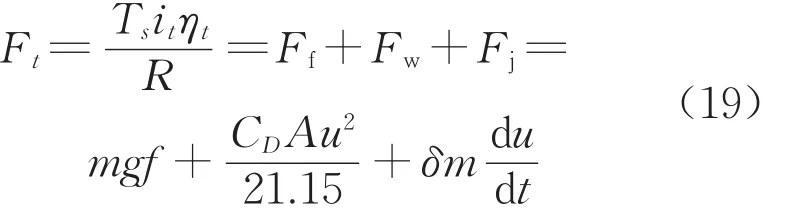
由式（19）可知，當電機到達恒功率區域時，電機轉矩與汽車行駛加速度成一次線性關系。結合電機啟動到加速過程中由恒轉矩到恒功率的變化過程，可以得到轉矩與時間的關系如圖23所示。

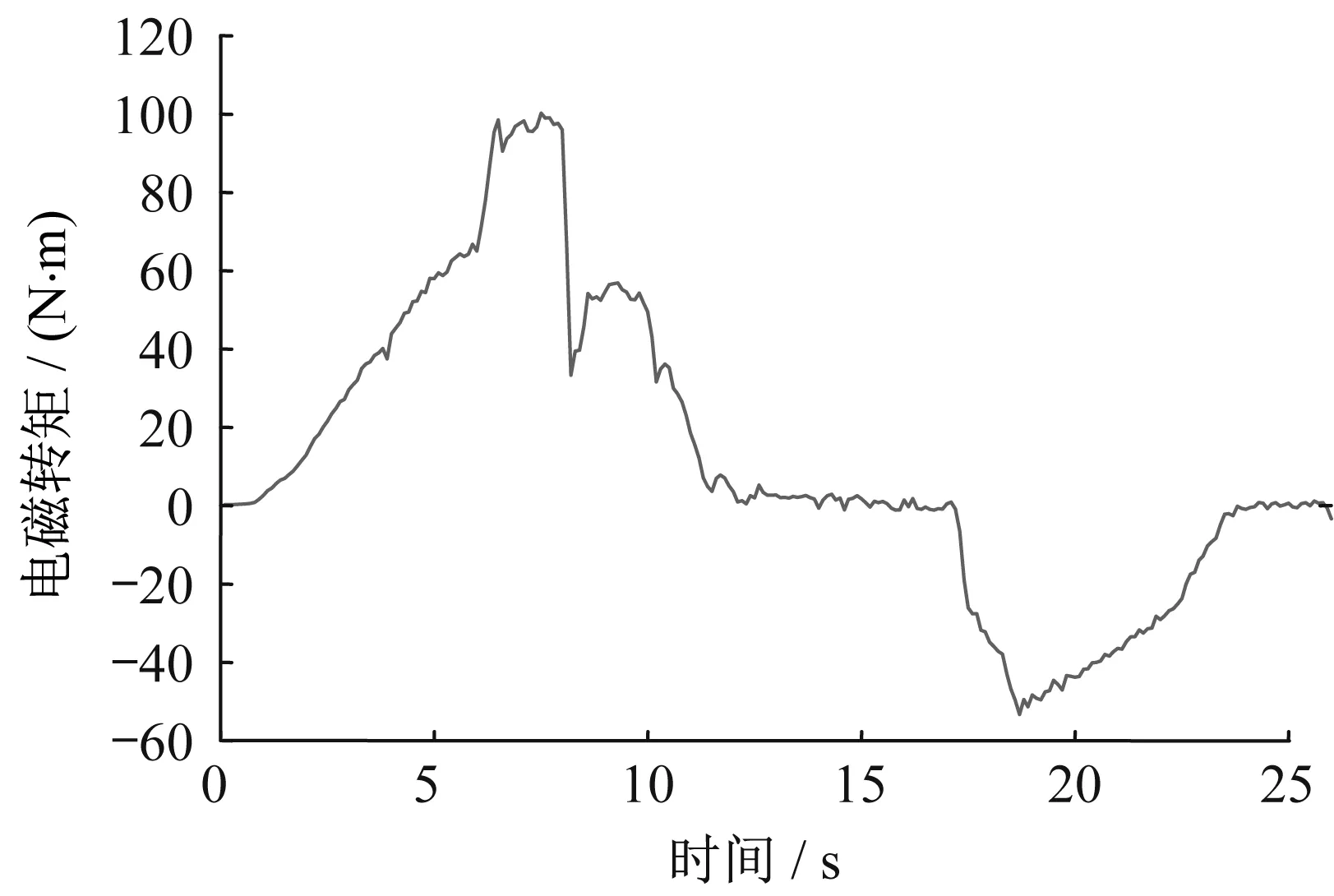
圖23 電動機輸入轉矩曲線Fig.23 Motor input torque curve

由圖23可知，在0～6s的時間內電機啟動，轉矩呈現梯形上升；在6～8s時間內電機為恒轉矩的運行狀態，8s之后，電機工作在恒功率區域內，與汽車車速成正相關。對于電機轉速，與汽車車速成正比。計算如下：

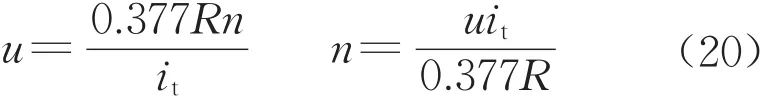
式中：u為汽車車速；it為傳動比；R是輪胎半徑；n是電機轉速。

與電機轉矩對應，當電機轉矩結束恒功率區域時，電機轉速達到額定轉速4 000r·min-1。至此可確定電機的機械角轉速隨時間變化的曲線如圖24所示。

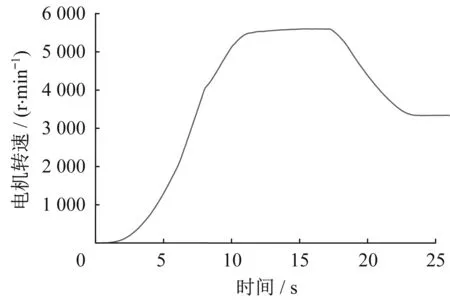
圖24 電動機輸入轉速曲線Fig.24 Motor input speed curve

對于整個電驅系統，包括DC/AC信號觸發和永磁同步電機反饋環在內的控制部分如圖25所示。

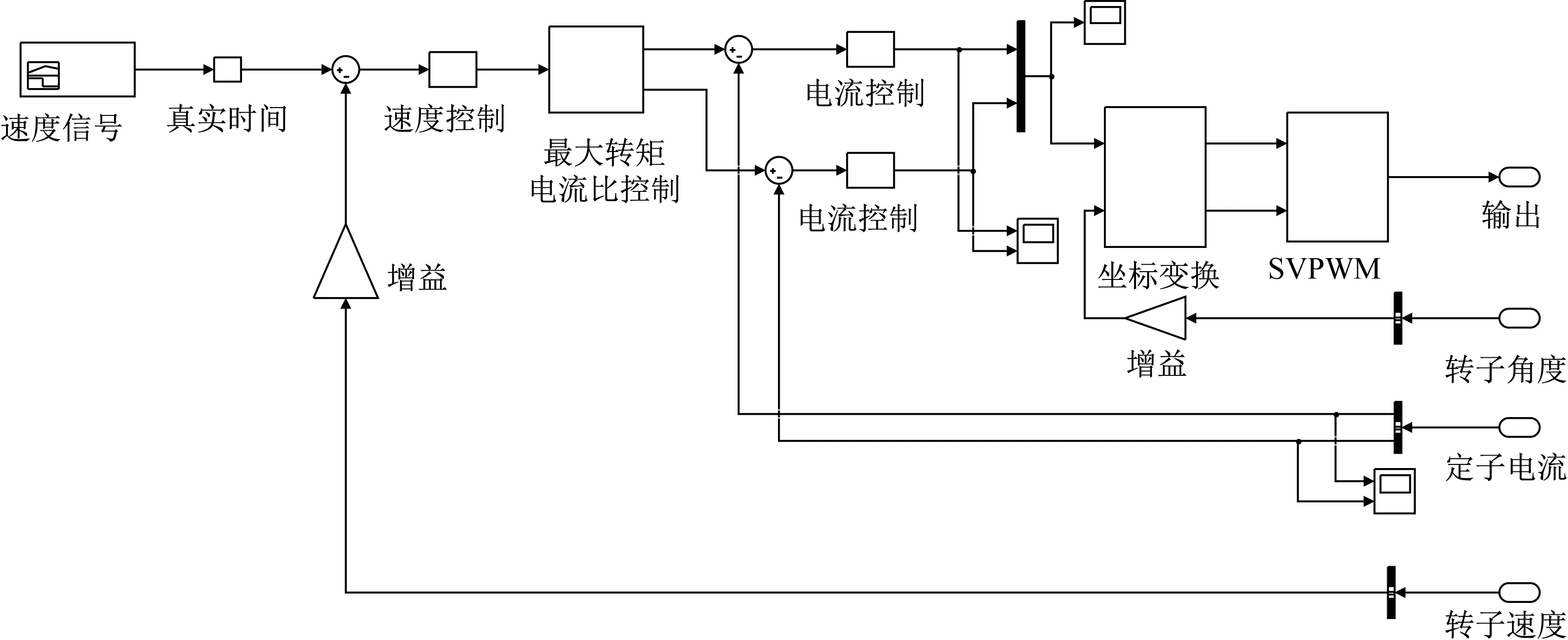
圖25 PMSM最大轉矩電流比控制模型Fig.25 PMSM maximum torque current ratio control model

綜上所述，結合前文電池包阻抗模型、全橋DC/AC模塊、電機模塊以及控制部分，動力電池系統的模型如圖26所示。

其中，圖26中的控制部分為圖25所示逆變器信號和電機控制部分，電機的輸出RT模塊用于控制離散時間變量，使采樣時間間隔與逆變器的周期保持一致，以提高仿真速度。仿真所得電機轉速和轉矩如圖27所示。

對比圖27和圖23～圖24可知，仿真的電機轉速和轉矩結果與給定電機轉矩和轉速幾乎保持一致。也就是說在最大轉矩電流比法的控制下，電機的輸出轉矩和轉速基本完全響應加減速工況下的輸入轉矩和轉速，可見該電驅系統仿真模型是準確的。

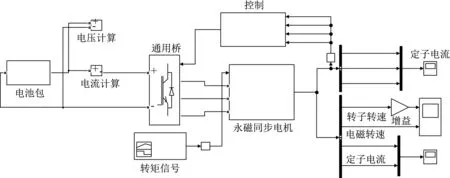
圖26 動力電池系統電磁仿真模型Fig.26 Electromagnetic simulation model of power battery system

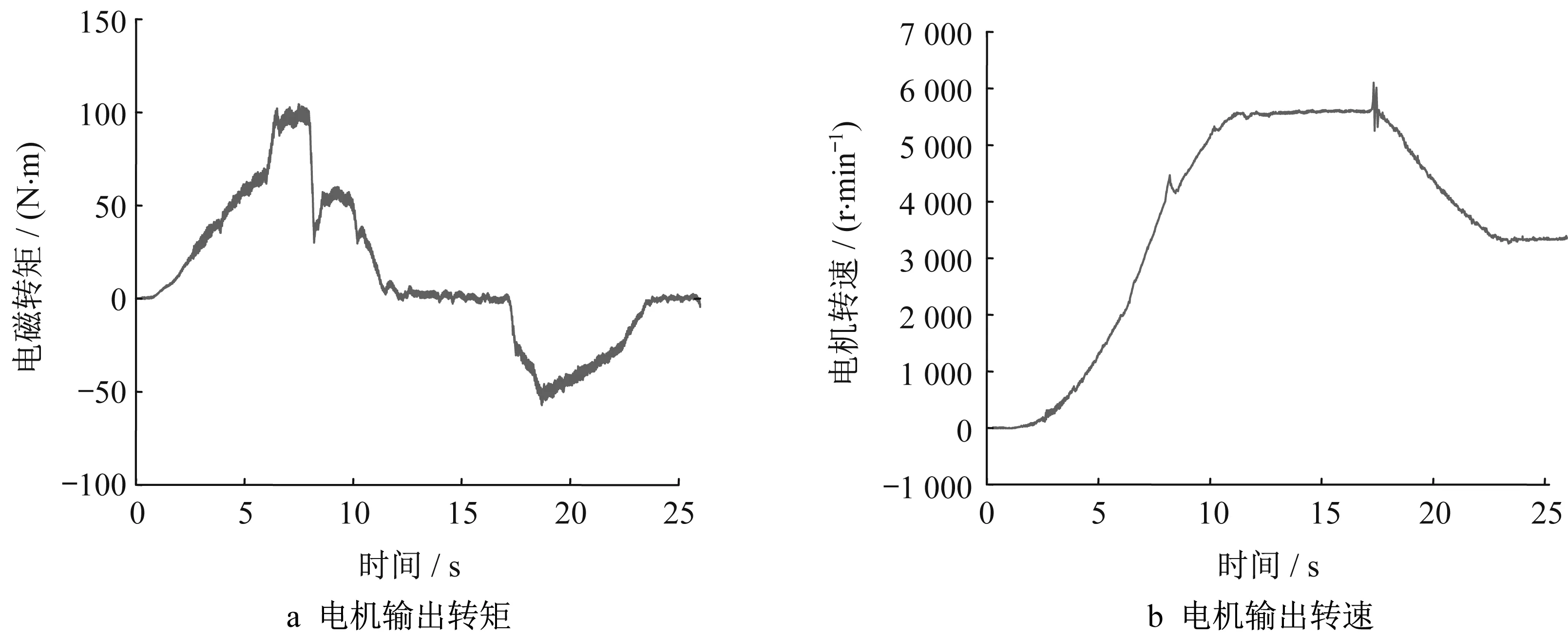
圖27 電驅系統仿真電機輸出轉矩和轉速結果Fig.27 The output torque and speed of the simulated motor of the electric drive system

3.2 實車行駛測試驗證

為了驗證研究的電池包及電驅系統模型的準確性，需要在實車上進行行駛試驗。

圖28a為大眾凌度樣車，圖28b為數據采集端，PC端的CANoe軟件通過USB與CANoe硬件相連，CANoe硬件通過光纖與電動車上的兩路CAN相連。電池包內部出現電磁干擾時，電驅系統及逆變器模塊出現劇烈的電流電壓變化。為模擬電池包內部電磁干擾的情況，實車運行工況為從0加速到70km·h-1再減速到0。

圖28 電動汽車實車工況數據采集布置總圖Fig.28 General layout of data collection for electric vehicle actual vehicle operating conditions

將實車上采集到的車速隨時間變化情況進行解碼，通過動力學計算得到電機轉矩及轉速的變化情況，作為電驅系統的輸入，模擬仿真得到電池包兩端母線電流。同樣對電池包兩端母線電流進行解碼，由此可得到實車上的電池包母線總電流，將該電流與前述仿真電流結果進行對比，如圖29所示。

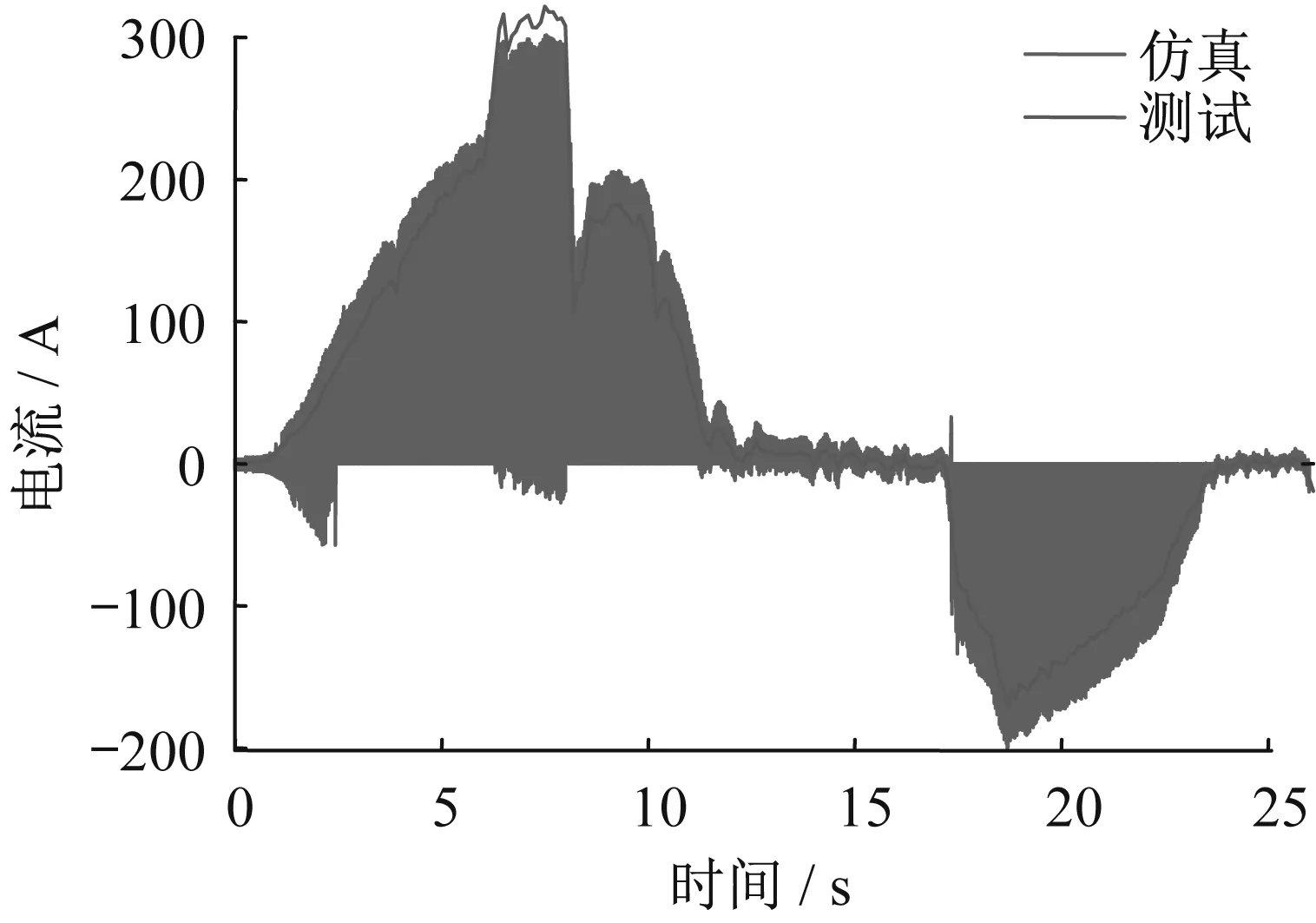
圖29 電池包兩端母線電流仿真與測試對比Fig.29 Comparison of current simulation and test on both sides of the battery pack

由圖29可知，仿真和實測電流基本保持一致，驗證了該干擾源模型的準確性。加速時，電池包處于放電狀態，電流為正；剎車時，電池包回收制動能量，電流為負，電池包處于充電狀態。起步達到最高車速以及開始制動時，母線電流波動較大，容易引起電磁干擾問題。實車測試所得電流曲線為仿真電流結果的包絡，這主要是因為CAN總線的數據傳輸速率最大為500kbit·s-1，采用CANoe采集總電流數據時采樣精度約為100kHz，而逆變器全橋電路的開關頻率為10kHz，因此CANoe采集到的數據中未體現IGBT關斷的瞬間；而在仿真模型中，采樣時間間隔設置為最大10ns，因此在一個IGBT的開關周期內，可以采集約1 000次數據，因此能夠體現開關器件的開通和關斷狀態。實測結果和仿真結果在包絡上一致，說明模型精度能夠接受。

4 結論

考慮到純電動汽車上主要的電磁干擾源為電驅系統，而電池包又直接與電驅系統相連，本文對包括電池包、電機、電機控制器在內的整個動力電池系統干擾源進行了建模仿真，并通過實車測試驗證了仿真模型的準確性。

電池包采用搭建的全頻段等效電路阻抗模型，電機采用三對極凸極式永磁同步電機，采用查表法最大轉矩電流比進行控制，空間矢量脈沖寬度調制產生逆變器6路IGBT的使能信號。電驅系統運行在加減速工況下，系統模型的輸入為電機轉矩和轉速，在仿真模型中監測電池包直流母線上的總電流。

為驗證該模型的準確性，同樣采集實車母線總電流，用DBC對實車數據進行解碼，將實測電流與仿真模型所得電流進行對比，發現在加（減）速度較大的區間范圍內，電流的波動較強烈，容易引起動力電池系統電池單體上的電壓波動，仿真數據與實測數據一致，仿真結果可以對動力電池系統母線上的總電流干擾有一個準確的預測。