施工期混凝土重復荷載作用下的受壓應力-應變關系
彭 剛, 胡曉鵬,2, 牛荻濤,2, 王 靜
(1.西安建筑科技大學 土木工程學院, 陜西 西安 710055;2.西安建筑科技大學 省部共建西部綠色建筑國家重點實驗室, 陜西 西安 710055)
中國幅員遼闊、地震多發,加之基礎設施建設正處于快速發展中,地震發生時很多混凝土結構尚處于施工階段.相關統計數據表明[1],汶川地震時,中國約有200多億平方米的在建建筑物遭受了6度以上的地震作用.與正常使用階段相比,施工階段的混凝土結構具有混凝土性能時變、荷載效應復雜、受模板支撐體系作用明顯和結構傳力機制不成熟等特征[2].因此,施工期混凝土結構在遭受地震作用時的破壞程度和破壞特征會明顯不同于正常使用階段.
對施工期混凝土結構震損特征進行研究是客觀評價施工期混凝土結構后續使用可靠性的基礎.近年來,隨著計算機技術的高速發展,數值模擬分析方法已成為研究施工期混凝土結構震損特征的重要手段,然而數值模擬分析方法的使用需要以材料的本構關系模型為基礎.遭受地震作用的施工期混凝土結構處于重復受荷載的狀態,因此,施工期混凝土重復荷載作用下的本構模型對施工期混凝土結構震損特征的研究起著至關重要的作用.
目前,部分學者基于單調加載試驗,提出了施工期混凝土單調荷載作用下的受壓應力-應變本構關系模型,為施工期混凝土結構的可靠性分析提供了一定的理論支撐[3-8].然而,尚未有施工期混凝土重復荷載作用下的受壓應力-應變本構關系方面的研究.可靠的重復荷載下施工期混凝土本構關系計算模型的缺乏,給施工期混凝土結構震損特征的研究造成了一定的困難.
本文通過重復荷載作用下施工期混凝土的受壓試驗,分析了重復荷載作用下混凝土試件受壓應力-應變全曲線的各特征參數(峰值應力、峰值應變、外包絡線、卸載曲線和再加載曲線等)隨混凝土齡期的變化規律,建立了重復荷載下施工期混凝土的受壓應力-應變關系模型,為施工期混凝土結構震損特征研究提供可靠的支撐.
1 試驗
1.1 原材料及配合比
水泥為P·O 42.5普通硅酸鹽水泥,細度1)為0.6%,其主要性能指標見表1;細骨料為灃河河沙,細度模數為2.9,堆積密度為1450kg/m3;粗骨料為粒徑5~20mm的碎石,堆積密度為1550kg/m3;高效減水劑為PCA?-I聚羧酸高性能減水劑,減水率在20%左右,1h內無坍落度損失.混凝土試件的配合比見表2.

表1 水泥的主要性能指標

表2 混凝土試件的配合比
1.2 試件設計及制作
混凝土強度等級為C30、C40和C50,齡期分別為8、16h以及1、3、7、28d.試件采用組合鋼模具澆筑成型,尺寸為100mm×100mm×300mm,每組3個試件.對齡期小于1d的試件,標準養護至開始試驗時拆模;對齡期大于等于1d的試件,標準養護 1d 后拆模,將其放置在標準養護室中養護至設定齡期.
1)文中涉及的細度、減水率等均為質量分數.
1.3 加載制度
用改進的WAW-1000系列微機控制電液伺服萬能試驗機對不同齡期的混凝土試件進行重復加、卸載試驗,采用2個固定架以及位移計并借助TDS-602動態數據采集儀記錄試件的荷載及軸向變形,位移計精度為0.01mm,固定架間距為200.00mm,試驗裝置示意圖見圖1.為了保證試件軸心受壓,首先對試件進行預加載,加載至5kN時觀察2個位移計讀數是否相近,若相差過多則停止試驗,重新進行對中.試驗采用位移控制的方式進行等位移增量加載,每級加載位移增量為0.05mm.加載至預定應變值后卸載至荷載為零,加、卸載速率均為0.10mm/min,試件完全破壞時停止試驗.

圖1 試驗裝置示意圖Fig.1 Schematic diagram of test equipment
2 結果與分析
2.1 試件破壞過程
圖2以C30混凝土試件為例,給出了不同齡期混凝土試件的破壞形態.短齡期的試件破壞為漿體自身、漿體-粗骨料之間產生黏性錯動,粗骨料無破壞,破壞面較為模糊;長齡期的試件破壞為漿體裂縫、漿體-粗骨料界面裂縫、個別粗骨料斷裂裂縫的延伸所導致,破壞面較齊整.

圖2 C30試件破壞形態Fig.2 Failure modes of C30 specimens
2.2 力學性能參數及其計算模型
表3為重復荷載作用下試件的力學性能參數.表3中:σ1,t、ε1,t、E0,t、Ep,t分別為齡期t時混凝土試件的峰值應力、峰值應變、初始割線模量、峰值點割線模量;E0,t取應力0.4σ1,t處對應的割線模量,Ep,t取峰值應力及峰值應變點處的割線模量;各性能參數采用3個試件測試值的算術平均值,3個測試值中的最大值或最小值中如與中間值的差值超過中間值的15%時,則取中間值.由表3可見:隨齡期的延長,混凝土試件的峰值應力增加,峰值應變減小,初始割線模量、峰值點割線模量均有不同程度的增大;相比于初始割線模量,峰值點割線模量增長幅度相對較小.
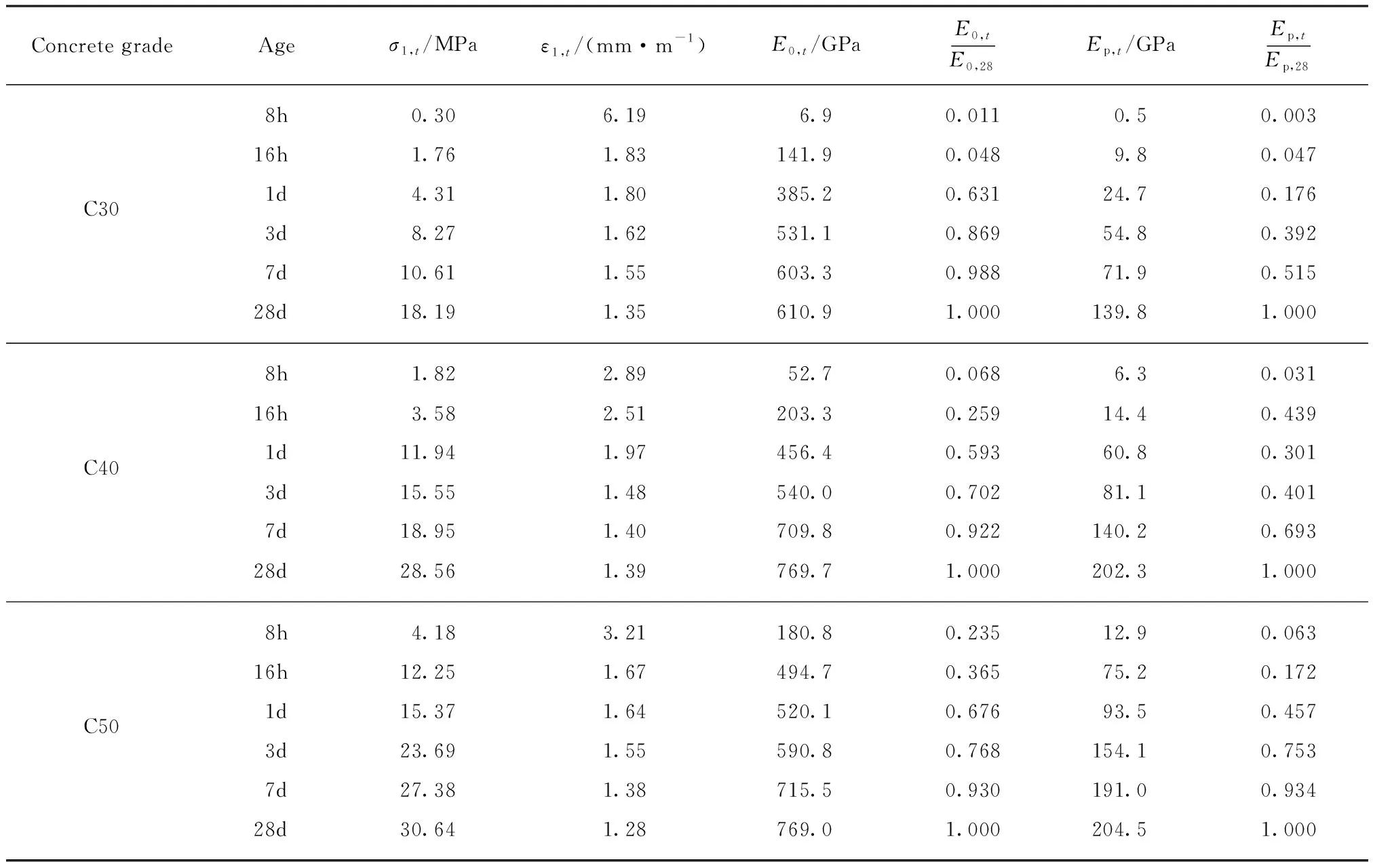
表3 重復荷載作用下試件的力學性能特征參數
圖3為重復荷載作用下混凝土試件的相對峰值應力σ1,t/σ1,28、相對峰值應變ε1,t/ε1,28隨齡期的變化規律.由圖3(a)可見:隨著齡期的延長,混凝土試件的相對峰值應力呈指數型增大;隨著混凝土強度的增大,相對峰值應力的增長速度增大.這一規律與早齡期混凝土抗壓強度隨齡期的時變規律基本一致[9-10].由圖3(b)可見:隨著混凝土齡期的延長,混凝土試件的峰值應變呈負指數型減小,1d內混凝土相對峰值應變急劇減小,1d后相對峰值應變減小速度明顯減緩并逐漸趨于穩定;3種強度等級混凝土試件峰值應變隨齡期延長而減小的幅度基本一致.分別對3種強度等級混凝土的相對峰值應力、相對峰值應變與齡期的對應關系進行擬合,得到如下的關系表達式[8]:
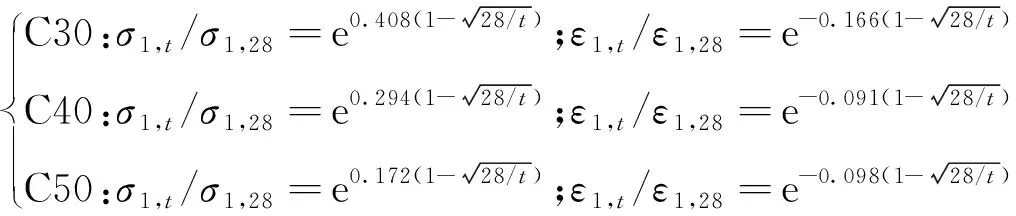
(1)

圖3 重復荷載作用下混凝土試件的相對峰值應力、相對峰值應變隨齡期的變化規律Fig.3 Variations of relative peak stress and relative peak strain of concrete specimens with age under repeated loading
2.3 受壓應力-應變全曲線、外包絡線及其計算模型
圖4~6分別為重復荷載作用下C30、C40、C50混凝土試件的受壓應力-應變(σ-ε)全曲線.由圖4~6可見:重復荷載作用下不同齡期、混凝土強度等級的混凝土試件受壓應力-應變全曲線的卸載曲線、再加載曲線均有明顯不同.沿應力-應變全曲線外輪廓描線,可得其相應的外包絡線,如圖7所示.由圖7可以看出:不同齡期混凝土的外包絡線形狀相似;隨著混凝土齡期的延長,外包絡線上升段及下降段均變得陡峭,峰值應力、初始割線模量及峰值點割線模量迅速增大,峰值應變逐漸減小,破壞特征逐漸顯現出脆性破壞的特征;對齡期相同的混凝土試件,混凝土設計強度越高,其初始割線模量、峰值點割線模量及峰值應力越大,峰值應變越小,且混凝土試件的彈性模量隨齡期增長的速度越快.這與單調受壓作用下施工期混凝土應力-應變全曲線得到的結論基本一致[5-7].
混凝土重復荷載作用下的外包絡線與單調加載的全曲線十分接近,通常采用單調加載全曲線表達式近似描述外包絡線的曲線形態[11-13].采用式(2)的分段式曲線方程對不同齡期混凝土的外包絡線進行擬合分析.
(2)
式中:x=ε/ε1,y=σ/σ1,σ1、ε1分別為峰值應力和峰值應變;ac和bc分別為外包絡線曲線上升段和下降段參數,其值取決于混凝土的強度等級和齡期,其擬合結果見表4.
2.4 卸載曲線及其方程
由混凝土的受壓應力-應變全曲線外包絡線上的任一點(εu,σu)卸載至(εp,0),得到完全卸載曲線.將卸載時的應變εu和殘余應變εp分別除以峰值應變ε1,進行無量綱化處理,得到圖8所示的混凝土卸載應變比(εu/ε1)-殘余應變比(εp/ε1)的關系.由圖8可見:卸載應變比相同時,混凝土的殘余應變比隨齡期延長逐漸減小.這是因為隨著齡期延長,混凝土材料的“脆性”特征逐漸顯現,混凝土變形恢復能力逐漸減弱.參照文獻[13-14]的計算模型,對得到的卸載應變比εu/ε1與殘余應變比εp/ε1關系進行擬合分析,結果如下式所示.
εp/ε1=a1(εu/ε1)b1
(3)

圖4 重復荷載作用下C30混凝土試件的受壓應力-應變全曲線Fig.4 Compressive stress-strain curves of C30 concrete specimens under repeated loading

圖5 重復荷載作用下C40混凝土試件的受壓應力-應變全曲線Fig.5 Compressive stress-strain curves of C40 concrete specimens under repeated loading

圖6 重復荷載作用下C50混凝土試件的受壓應力-應變全曲線Fig.6 Compressive stress-strain curves of C50 concrete specimens under repeated loading

圖7 重復荷載作用下混凝土試件的外包絡線Fig.7 Envelope of concrete specimens under repeated loading

表4 外包絡線參數擬合結果
(4)
對試件的每次卸載過程(εu/ε1=0.0563~2.0243),以修正卸載應變比(ε-εp)/(εu-εp)為橫坐標、應力比σ/σu為縱坐標得到混凝土試件歸一化后的卸載曲線.圖9為齡期為8h的C30混凝土試件歸一化后典型的卸載曲線.由圖9可見:隨著修正卸載應變比的增大,卸載曲線下凹程度逐漸增大.這說明隨著加卸載次數的增加,混凝土內部損傷不斷積累,卸載過程中應變恢復滯后現象越來越明顯.

圖8 卸載應變比-殘余應變比的關系Fig.8 Relationship between unloading strain ratio and residual strain ratio
圖9中歸一化后的卸載曲線滿足冪函數的形式:
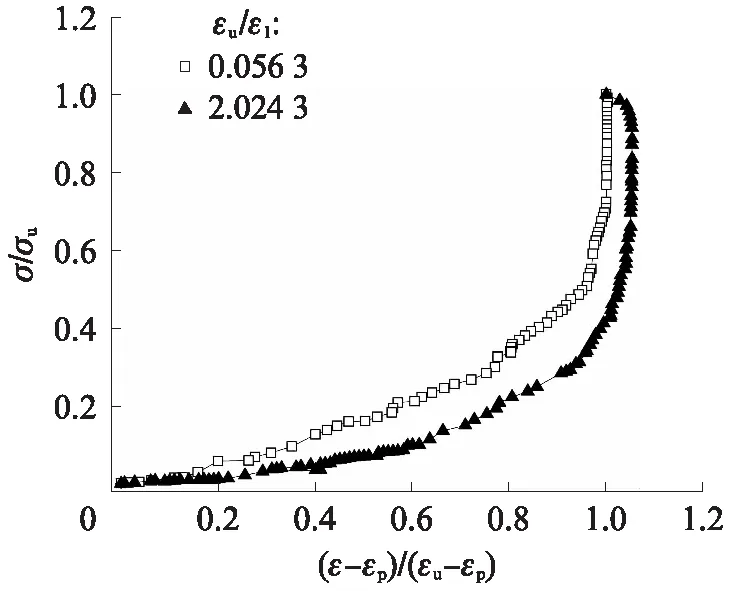
圖9 齡期為8h的C30混凝土試件歸一化后典型卸載曲線Fig.9 Typical unloading curves of C30 concrete specimens at 8h after normalized

(5)
式中:n為卸載參數.
參考文獻[12]的公式:
n=1+k(εu/ε1)
(6)
結合式(5)和式(6)對各條卸載曲線分別進行擬合分析,得到了卸載參數n與卸載應變比εu/ε1的對應關系,如圖10所示.由圖10可見:隨著齡期的延長、混凝土設計強度的提高,卸載參數n增大.這說明對同一卸載應變比的試件,齡期越長、混凝土設計強度越高,混凝土抵抗損傷積累的能力越強,卸載曲線下凹程度越緩,卸載曲線分布范圍越大.對圖10的結果進行擬合分析,得到系數k的表達式:

圖10 卸載參數n與卸載應變比的關系Fig.10 Relationship between unloading parameter n and unloading strain ratio
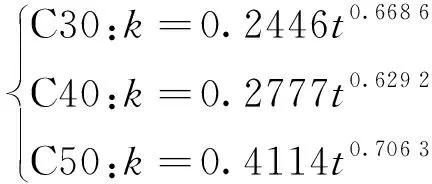
(7)
2.5 再加載曲線及其方程
從橫坐標上(εp,0)開始加載,至與外包絡線相切重合(εr,σr),此段為再加載曲線.將再加載時的起始應變εp和終點應變εr除以峰值應變ε1,進行無量綱化處理,得到再加載曲線起始應變比εp/ε1與終點應變比εr/ε1的關系,如圖11所示.由圖11可見:在相同再加載起始應變比下,隨著齡期的延長,混凝土抵抗損傷積累的能力增強,再加載曲線斜率逐漸減小,混凝土的終點應變比增大.對再加載曲線起始應變比εp/ε1與終點應變比εr/ε1的對應關系進行擬合,分析結果如下式所示.
εr/ε1=a2(εp/ε1)b2
(8)

(9)
(10)

圖11 再加載曲線起點應變比-終點應變比的關系Fig.11 Relationship between the starting strain ratio and the ending strain ratio of the reloading curves
對試件的再加載過程,以修正再加載應變比(ε-εp)/(εr-εp)為橫坐標、應力比σ/σr為縱坐標,得到混凝土試件歸一化后的再加載曲線.圖12為齡期8h的C30混凝土試件歸一化后的再加載曲線.由圖12可見:施工期混凝土試件再加載曲線存在2種形狀,當再加載曲線在全過程上升段(ε≤ε1)與外包絡線上升段相切時,曲線斜率單調減小,至切點處曲線斜率仍大于零,曲線上無拐點;當再加載曲線在全過程下降段(ε>ε1)與外包絡線下降段相切時,曲線斜率先增后減,曲線切點處斜率小于零,存在拐點.
基于文獻[12-13]的計算模型,對修正再加載應變比(ε-εp)/(εr-εp)與應力比σ/σr的對應關系進行擬合分析,分析結果見下式:
(11)
式中:m、q分別為再加載曲線參數.
m、q可通過試驗數據擬合確定,擬合結果見表5.由表5可見:再加載曲線參數m隨著齡期的延長而增加,當齡期≥16h后再加載曲線參數q趨于定值.

圖12 齡期8h的C30混凝土試件歸一化后再加載曲線Fig.12 Normalized reloading curves of C30 concrete specimens at 8h

表5 再加載曲線參數m、q取值
3 結論
(1)隨著齡期的延長,混凝土試件的彈性變形階段延長,同一應力水平下試件的軸向變形減小,裂縫寬度、長度增長速度減緩,試件破壞越慢,破壞面越齊整.
(2)隨齡期的延長,混凝土試件的峰值應力增大,峰值應變減小;初始割線模量、峰值點割線模量增大,但峰值點割線模量增長幅度相對較小;混凝土設計強度越大,峰值應力增加趨勢越明顯.
(3)隨著齡期的延長,混凝土試件的外包絡線上升段及下降段均變得陡峭,破壞特征逐漸顯現出脆性破壞特征.

