鐵道車輛柔性轉向架蛇行頻率分析方法

干鋒,戴煥云,羅光兵,楊震寰

(西南交通大學 牽引動力國家重點實驗室，四川 成都 610031)*

鐵道車輛在軌道上運行，依靠一定形狀的車輪踏面和軌道型面相互配合來完成直線行走和曲線通過等運動，如圖1所示.自由輪對在軌道上運行，由于踏面是具有一定錐度的錐形，會產生一種特有的自激振動(輪對橫向移動同時繞其中心垂向轉動)，這種運動稱為輪對蛇行運動.

圖1 輪對蛇行運動及波長

蛇行運動作為鐵道車輛的特有現象，其運動穩定性直接關乎車輛運行品質，近年來，我國的高速鐵路運營里程迅速增加，高速動車組運行過程中出現的蛇行失穩問題日益凸顯.大量學者對高速動車組的蛇行失穩現象展開研究.Polach[1]指出等效錐度曲線的非線性會對車輛的臨界速度和分叉類型產生影響，提出了一種用來評估輪軌關系的非線性參數.我國動車組在運營中出現的二次蛇行失穩現象與等效錐度的非線性密切相關，研究表明[2-5]，當等效錐度偏大且出現負斜率非線性特性時，動車組容易出現頻率一般為7～9Hz的二次蛇行失穩現象，該蛇行運動模態易與車體一階菱形模態耦合，出現嚴重惡化車輛運行平穩性和舒適度的“抖車”現象.這種現象可通過車輪鏇修、鋼軌打磨和提升車體一階菱形模態頻率加以解決.何旭升等[6]通過動車組振動測試指出輪軌等效錐度偏小時，動車組容易出現主頻為1.5Hz的一次蛇行運動.池茂儒等[7]指出我國高速鐵路存在鋼軌打磨偏差，軌肩欠打磨時容易導致等效錐度變大，造成車輛二次蛇行失穩；軌肩過打磨易導致等效錐度偏小，容易造成車輛一次蛇行失穩.

由以上研究成果可知，高速動車組的蛇行運動頻率與波長等參數對動車組的運行品質有很大影響，為車輛系統動力學的研究重點.1885年，德國學者Klingel[8]推導了計算自由輪對蛇行運動頻率和波長的Klingel公式，EN15302[9]和UIC519[10]標準計算等效錐度的過程中均使用了該公式.但實際運行的動車組轉向架均為具有一系懸掛的柔性轉向架，其蛇行運動頻率與波長介于自由輪對和剛性轉向架之間，需要通過理論推導或仿真計算來確定其蛇行運動波長與頻率.日本學者ShiroKoyanagi[11-12]于1991年提出了柔性轉向架蛇行運動波長的簡化計算方法并通過實測數據得到了驗證，但該蛇行運動方程將車輪簡化為錐形踏面，未考慮實際車輪踏面的強非線性，不能反映不同輪對橫移量下輪對蛇行頻率的變化，因此該公式不能直接應用于實際輪對和構架蛇行波長計算過程中.而蛇行運動對鐵道車輛穩定性和平穩性具有顯著影響，故有必要提出新的柔性轉向架蛇行運動公式，以研究車輛在實際車輪踏面錐度下及不同輪對橫移量下的輪對蛇行運動規律.

本文推導了自由輪對縱向、橫向和搖頭運動的三個一階微分方程，并將該方程作為蛇行運動的激勵代入考慮一系懸掛的柔性轉向架二階微分方程中.該二階微分方程考慮了轉向架的縱向、橫向和搖頭運動，結合蛇行運動特征，計算不同輪對橫移量下的構架蛇行頻率.并將計算結果與國內某型時速350 km動車組的實測構架加速度頻譜進行比較，從而驗證該方程的準確性和有效性.

1 自由輪對蛇行運動

1.1 自由輪對蛇行運動方程推導

結合圖1中的蛇行運動過程，以下從兩方面進行分析：

(1)輪對有橫移無搖頭時

當輪對有橫移無搖頭，即y≠0,θ=0°時，左輪接觸半徑為Rl，右輪為Rr，左輪接觸點距輪對中心距離為Ll，右輪為Lr(見圖2(a)).此時車輪以w的角速度向前滾動時，左輪接觸點的滾動速度為vl，右輪為vr.

(1)

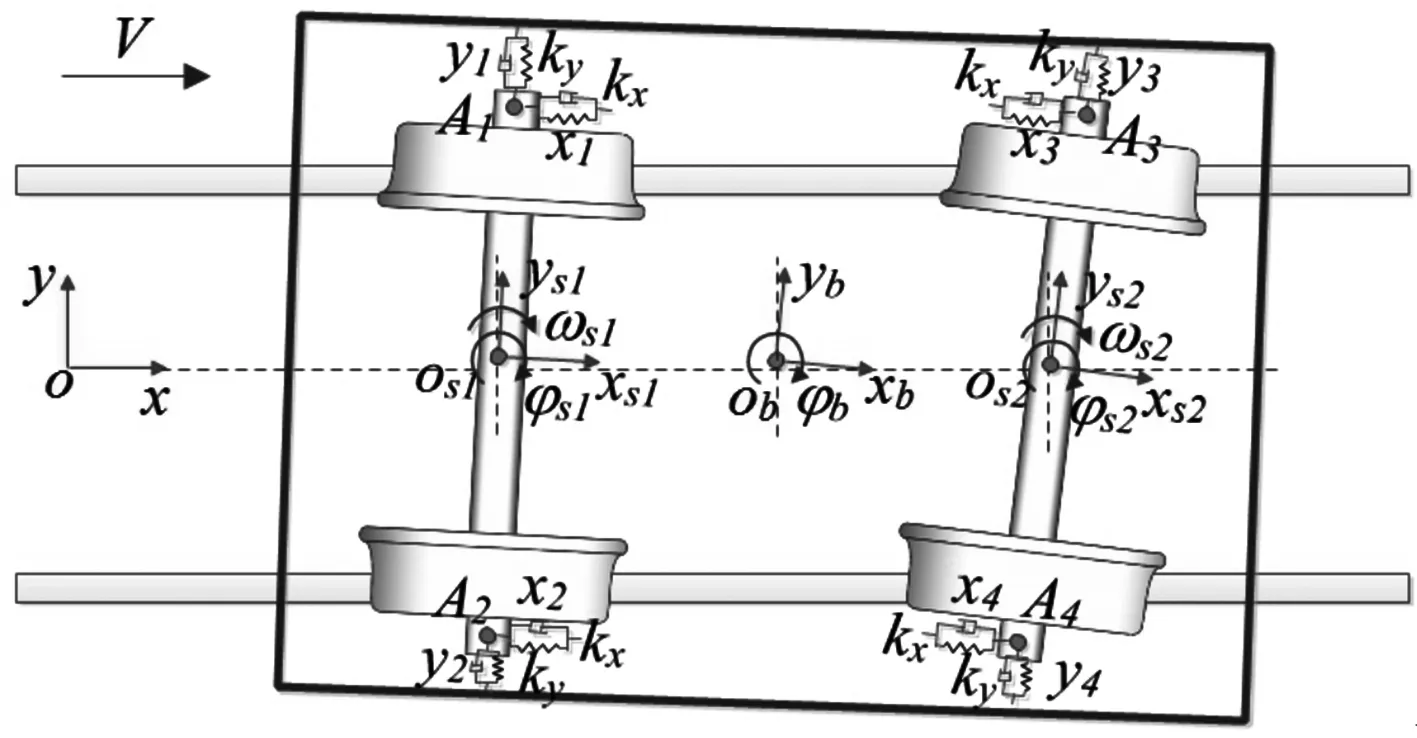
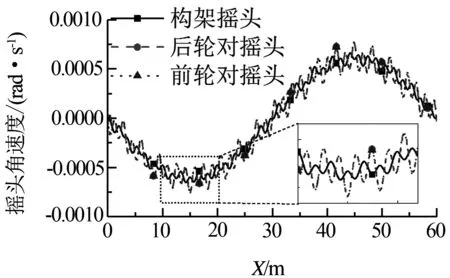
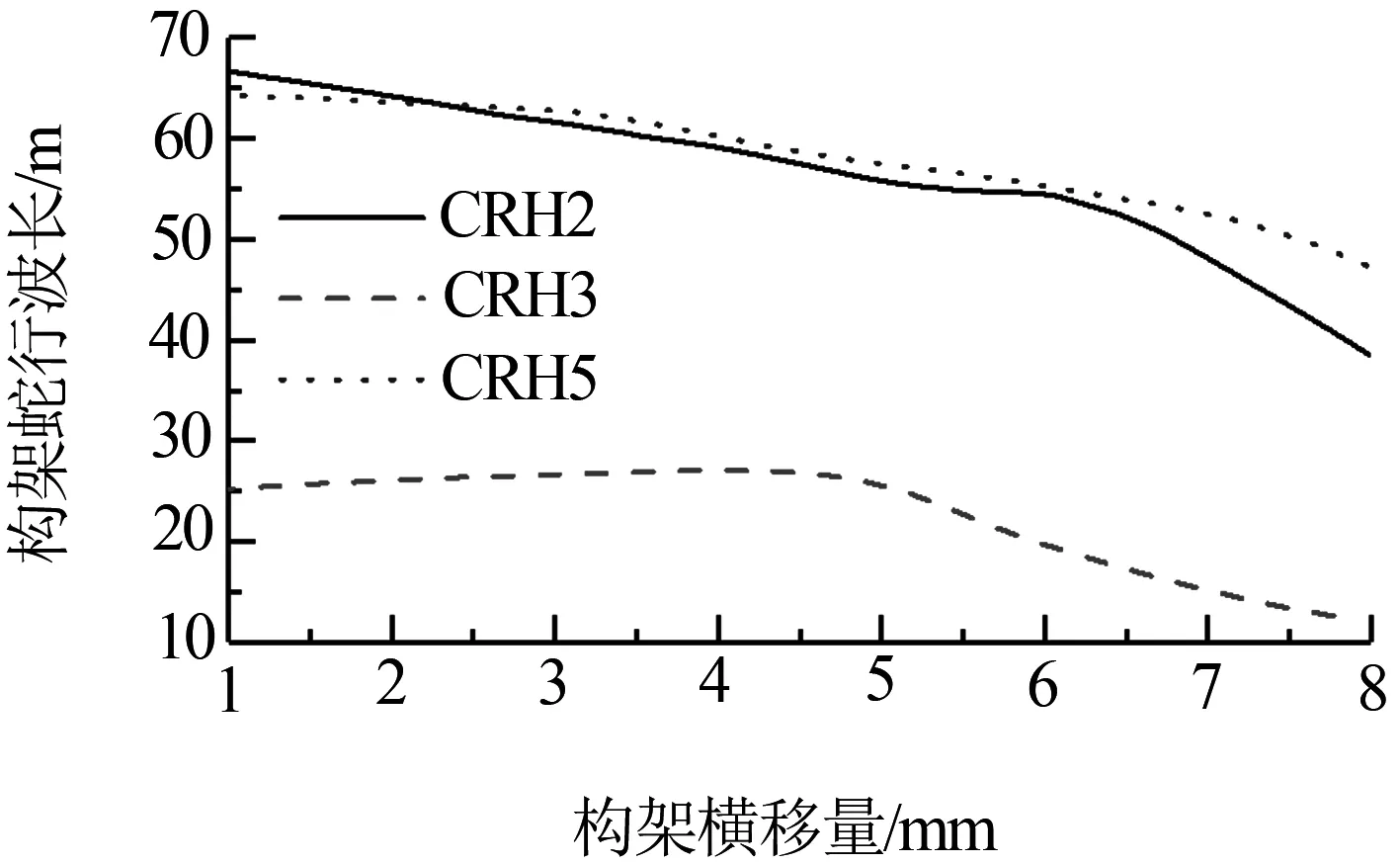
當vl>vr時，輪對的瞬時搖頭中心o′在軌面右側，反之vl

此時搖頭角速度φ可由下式得出：

(2)

由此搖頭中心o′距右側接觸點的距離Rφ和搖頭角速度φ分別為：

(3)

輪對前進速度和左右側縱向蠕滑率公式如下：

(4)

此時輪對前進速度v0與車輪沿軌道運行速度v一致，即v=v0.

(2)輪對有橫移有搖頭時

當輪對有橫移有搖頭時，輪對前進速度與車輪

沿軌道運行速度具有一定的搖頭角θ，此時車輪沿軌道運行速度v=v0cosθ,輪對橫移速度vy=v0sinθ(見圖2(b)).

由此得到以下微分方程：

(5)

其中，Rl,Rr,Ll,Lr均為y和θ的函數.

圖2 輪對蛇行運動分析

1.2 輪對蛇行運動對比分析

以S1002CN踏面和CHN60軌面為例(見圖3)，采用矢量法[3]實時計算輪軌接觸點并求解微分方程(5)，計算輪對初始橫移3 mm下的蛇行運動，如圖4所示.

(a) 踏面 (b) 軌面

圖4 輪對橫移量為3 mm時橫移和搖頭蛇行運動

圖4中可以看出，當給定初始輪對橫移量為3 mm時，輪對將做±3 mm的蛇行運動，同時輪對的橫移和搖頭相位角相差90°.

由此得到橫移或搖頭波長，可根據Klingel公式得到此時輪對橫移量下的等效錐度值.

計算0～12 mm輪對橫移量下蛇行運動波長和等效錐度，并與UIC519標準結果進行對比如圖5所示.

(a) 等效錐度 (b)蛇行運動波長

圖5可以看出由自由輪對蛇行運動公式得到的等效錐度和蛇行運動波長變化與UIC519標準得到的結果一致，從而驗證了公式(5)的正確性.

2 柔性轉向架蛇行運動方程

我國高速動車組轉向架均由一個構架和兩條輪對組成，中間采用一系懸掛進行連接，通過安裝在構架上的電機驅動安裝在車軸上的齒輪箱，帶動輪對向前滾動，實現列車的牽引和制動.由于車輪型面近似錐形，左右車輪通過車軸連接后轉速相同，當輪對橫向偏移后會產生類似于蛇行的自激振動.因此柔性轉向架蛇行運動方程必須體現輪對蛇行運動的特性和一系懸掛對前后輪對運動的約束.

2.1 柔性轉向架蛇行運動簡化計算方法

令轉向架軸距之半為Lb，同一輪對一系簧橫向間距之半為Ls，左右輪接觸點橫向間距之半為Ls1，r為車輪半徑，γ為等效錐度，則自由輪對蛇行運動波長λw為：

(6)

剛性構架蛇行波長λbg為：

(7)

柔性構架蛇行波長λbf為：

(8)

f為縱向和橫向蠕滑系數的平均值.

2.2 柔性轉向架蛇行運動精確計算方法

建立如圖6所示的柔性轉向架計算模型.令A1,A2,A3,A4分別為一系簧和前后輪對的四個連接點，其坐標分別為A1(-Lb,Ls),A2(-Lb,-Ls),A3(Lb,Ls),A4(Lb,-Ls)，kx,ky分別為一系簧的縱向和橫向剛度，yb,φb分別為構架的橫移和搖頭角，xs1,ys1,φs1分別為后輪對的縱向、橫向位移和搖頭角，xs2,ys2,φs2分別為前輪對的縱向、橫向位移和搖頭角，xb,yb分別為

(a) 構架和輪對無搖頭運動

(b) 構架和輪對有搖頭運動

構架的縱向和橫向位移，x1,y1分別為后輪對左側一系簧的縱向和橫向位移，x2,y2分別為后輪對右側一系簧的縱向和橫向位移，x3,y3分別為前輪對左側一系簧的縱向和橫向位移，x4,y4分別為前輪對右側一系簧的縱向和橫向位移.

則根據二維旋轉矩陣可得一系鋼簧位移表達式為：

(9)

令輪對質量為ms，搖頭轉動慣量為Isz，構架質量為mb，搖頭轉動慣量為Ibz，則構架動力學方程可表示為：

(10)

結合輪對蛇行運動方程，前后輪對的縱向、橫向和搖頭速度可表示為：

(11)

式中,前后輪對的縱向、橫向和搖頭速度方程由自由輪對蛇行運動方程和加速度積分方程兩部分組成.自由輪對蛇行運動方程作為輪對自激振動的激勵作用于構架，而構架通過一系懸掛的約束來限制輪對的運動.

3 不同車型柔性轉向架蛇行頻率分析

以CRH2、CRH3和CRH5型車為例，采用上述建模方法分別計算在輪對橫移量為3 mm時前輪對、后輪對和構架的蛇行運動，計算參數如表1所示，計算結果如圖7所示.

在300 km/h運行速度下，令構架和前后輪對初始橫移量均為3 mm，搖頭角為0 mm，即ys1=ys2=yb=3，φs1=φs2=φb=0，計算構架和前后輪對的運動方程如圖7～圖9.

表1 不同車型計算參數表

(a) 橫移量

(b)搖頭角

(a) 橫移量

(b)搖頭角

(a) 橫移量

(b)搖頭角

由圖7～圖9知，各車型的輪對與構架蛇行波長較為接近.前后輪對同相運動，搖頭角幅值相近，略大于構架搖頭角幅值.三種車型中，CRH3型車蛇行頻率最高，可達3.13 Hz，CRH2型車蛇行頻率為1.38 Hz , CRH5型車蛇行頻率為1.36 Hz.

在300 km/h運行速度下，計算CRH2、CRH3和CRH5型車構架在不同構架橫移量下構架蛇行波長和頻率如圖10所示.

(a) 構架蛇行波長

(b) 構架蛇行頻率

由圖10知，構架橫移量在1～8 mm時，CRH3型車的蛇行頻率最高，CRH2型車和CRH5型車的蛇行頻率較為接近.CRH3型車在構架橫移1～5 mm時，蛇行頻率會小幅降低，大于5 mm后蛇行頻率會較快增長；CRH2型和CRH5型車的蛇行頻率會隨構架橫移量的增加而逐漸增長.

4 柔性構架蛇行運動分析驗證

4.1 試驗數據分析

實測國內以350 km/h高速運行的某型動車組車輪踏面鏇修后運行13萬公里時軸箱、構架端部和車體枕梁振動加速度如圖11所示.由于構架蛇行運動頻率較低，因此對振動加速度信號進行了低通50 Hz濾波處理.

(a) 軸箱橫向和垂向振動加速度

(b) 構架端部橫向和垂向振動加速度

(c) 車體枕梁橫向和垂向振動加速度

在圖11數據基礎上截取勻速350k m/h運行時軸箱、構架和車體枕梁振動加速度信號如圖12所示.

(a) 軸箱橫向和垂向振動加速度

(b) 構架端部橫向和垂向振動加速度

(c) 車體枕梁橫向和垂向振動加速度

從圖12中可以看出，經50 Hz低通濾波后，軸箱垂向和橫向加速度振動幅值接近，而構架端部和車體枕梁垂向振動加速度均比橫向大，且出現明顯的低頻振動.

4.2 振動頻譜分析

分析圖12中軸箱、構架和車體枕梁振動加速度頻譜和加速區段短時FFT頻譜，分別如圖13所示.

從圖13中可以看出構架端部出現明顯的2.9、14.9和33.6 Hz振動頻率，其中33.6 Hz在軸箱垂向、構架端部橫向與垂向振動加速度頻譜中有體現；14.9 Hz在枕梁垂向、構架端部橫向和垂向振動加速度頻譜中有體現；2.9 Hz在構架端部橫向和垂向、車體枕梁橫向振動加速度頻譜中有體現.并且這些主頻在車輛加速區段形成明顯的振動能量集中帶，且隨著速度的變化而變化.

圖13 實測車輛350 km/h時軸箱、構架和車體枕梁振動頻譜

對上述頻率進行分析：車輛運行在該區段時線路使用的軌道板類型為CRTSⅡ型軌道板，其單塊長度為6 450 mm，相鄰軌道板板縫約為50 mm，相鄰軌道板間總長LT≈6 500 mm，則車輛勻速349 km/h的軌道板通過頻率為14.9 Hz；車輪半徑為0.46 m，則車輪轉頻為33.5 Hz，與圖13中實測頻率基本一致.因此確定14.9 Hz頻率來源為車輛通過CRTSⅡ型軌道板時頻率，33.6 Hz頻率來源為車輪轉動頻率.

4.3 構架蛇行頻率分析

實測高速動車組車輪鏇修后運行13萬公里左右時車輪踏面廓形如圖14所示，與標準CHN60軌面匹配時輪軌接觸關系如圖15所示.

(a) 左輪踏面

(b) 右輪踏面

實測車輪踏面與標準CHN60軌面匹配的輪徑差、等效錐度和輪軌接觸幾何關系如圖15所示.

(c) 輪軌接觸幾何關系

從圖14和圖15可以看出，左右車輪踏面在名義滾動圓附近出現凹型磨耗，左右車輪踏面磨耗外形不對稱，左右踏面上接觸點分布和輪徑差曲線也不對稱.輪對橫移3 mm時UIC519等效錐度為0.14.

高速動車組轉向架動力學參數如下：輪對質量為 1901.8 kg；輪對慣量Z為684.65 kg·m2；構架質量為2 280kg；構架慣量Z為2280 kg·m2；軸距之半為1.25 m；一系橫向距離為1 m；一系縱向剛度為14.7 MN/m；一系橫向剛度為6.5 MN/m.

根據式(10)和高速動車組轉向架動力學參數，以及實測車輪踏面輪軌接觸關系，仿真計算得到轉向架在不同運行速度下輪對橫移量和蛇行頻率的關系，如圖16所示.由圖知，輪對橫移3 mm，運行速度為350 km/h時的構架蛇行頻率為3.0 Hz，與圖13中實測頻率基本一致，因此確定頻率3來源為構架蛇行頻率，從而也驗證了式(11)的正確性.

圖16 不同運行速度下輪對橫移量和蛇行頻率關系

5 結論

(1)本文推導的與輪對橫移和搖頭相關的三個一階蛇行運動微分方程與基于輪對橫移的蛇行運動二階微分方程計算結果一致，可得到與 Klingel公式計算結果一致的等效錐度曲線;

(2)CRH2和CRH5型車的蛇行頻率較為接近且低于CRH3型車的蛇行頻率.CRH3型車在構架橫移1～5 mm時，蛇行頻率會小幅降低，大于5mm后蛇行頻率會較快增長；CRH2型和CRH5型車的蛇行頻率會隨構架橫移量的增加而逐漸增長;

(3)通過求解本文推導的柔性轉向架的二階微分方程得到與實測時速350km動車組的構架蛇行頻率基本一致的結果，驗證了該二階微分方程的正確性和有效性.