時速400km高速動車組動力學性能分析

王淇,崔濤,丁學彬,朱寶,張良泉

(中車唐山機車車輛有限公司， 河北 唐山 063000)*

高速列車的車輛動力學仿真分析研究大多局限于單一車輛，對整列列車的平穩性研究也多為單一編組模式[1].為了進一步研究列車的車輛動力學性能，掌握不同位置車輛的動力學性能差異，有必要建立一個多體動力學模型.劉宏友等人[2]建立了包含三輛拖車的列車動力學模型來研究高速列車的運行穩定性，其認為三車列車模型包含了頭尾車輛及中間車輛，已經能夠反映列車的動力學特性.羅仁等人[3]考慮了單車模型、5車編組列車模型和7車編組列車模型的情況，分析了列車的運行平穩性.結果表明，頭尾車輛的運行平穩性最差，中間車輛較好.池茂儒等人[4]考慮了列車在縱向、橫向以及垂向性能之間的耦合關系，建立了重載列車的三維空間耦合動力學模型.仿真結果表明：牽引工況下，頭尾車輛比中間車輛的動力學性能差；制動工況下，則中間車輛的相關性能較差.陸文教等人[5]針對某B型地鐵，采用多體動力學分析軟件UM進行建模，分析了車輪磨耗對輪對接觸損傷特性以及車輛動力學性能的影響.黃照偉等人[6]分析了不同運行里程下的車輪磨耗變化規律，討論了車輪磨耗對車輛動力學性能的影響.劉闖等人[7]通過對一列運行固定交路的動車組進行長期服役跟蹤測試，從試驗角度出發，對各磨耗階段的輪軌匹配對車輛動力學的影響進行了分析研究.

本文建立了由8節車輛組成的列車動力學仿真模型，基于已獲取的典型車輪型面磨耗規律，預測時速400 km動車組在不同磨耗狀態下的動力學特性.所分析的動力學性能包括運動穩定性、運行平穩性和運行安全性指標[8].分析了頭尾車輛以及中間車輛的動力學性能差異，研究了不同輪軌匹配關系對列車車輛動力學性能的影響.

1 車輛動力學模型

時速400 km及以上高速動車組采用高速轉向架，主要包括枕梁、構架、輪對、軸箱懸掛裝置、中央懸掛裝置、制動和牽引裝置.軸箱懸掛裝置包括轉臂定位、軸箱鋼彈簧和一系垂向減振器；中央懸掛裝置采用二系空氣彈簧，并安裝了二系橫向減振器和抗蛇行減振器、抗側滾扭桿、牽引拉桿，中央懸掛裝置還設有由間隙和橡膠塊提供的非線性橫向止檔；制動為軸盤和輪盤制動，牽引裝置采用Z字型牽引拉桿；在車輛之間沒有安裝縱向布置的車間減振器.

列車車輛動力學模型如圖1所示，列車系統的運動方程為：

(1)

圖1 時速400 km及以上高速動車組動力學模型

2 橡膠節點非線性動力學模型

橡膠具有強非線性，在不同加載幅值和頻率下動態剛度和阻尼各異.橡膠節點廣泛應用在轉臂節點等部位，使用橡膠件最簡單的力學模型是彈簧和阻尼并聯模型，但不能體現其非線性動態特性.一些學者提出了多種用于動力學仿真的橡膠件力學模型，例如彈簧、粘性和摩擦并聯Mats Berg模型；彈簧、摩擦和分數導數并聯模型等.本文根據動車組上大量的橡膠元件動態試驗結果，提出了非線性彈簧、非線性Maxwell模型和非線性阻尼并聯模型，具體如圖2所示，相較于前兩種模型，該非線性模型計算速度很快，不會影響車輛系統動力學仿真速度.

圖2 橡膠非線性力學模型

橡膠節點每一個動態試驗工況下得到的力-位移遲滯曲線，如圖3所示，其斜率和面積分別與剛度和阻尼相關.橡膠彈性元件的剛度通過極值法計算：

(1)

圖3 橡膠件力-位移遲滯曲線

力-位移遲滯曲線所包圍的面積與阻尼耗能相等，在一個循環周期內損耗的能量即是動態力F所做的功W：

(2)

設x0為激勵幅值，ω為振動角頻率，通過能量法求得橡膠件的等效線性阻尼cd：

(3)

移分段線性曲線.將乘以比例系數后的動態剛度與動態阻尼作為Maxwell模型的試驗數據，計算得到串聯阻尼力-速度非線性曲線、串聯剛度力-位移非線性曲線；由于試驗是在不同幅值和不同頻率下進行的，會得到多條曲線，cd曲線采用這些阻尼力-速度曲線的外包絡線，kd曲線采用這些剛度力-位移曲線的平均曲線，并沿位移軸放大.并聯阻尼主要是補充動態阻尼的不足部分，將以上阻尼力-速度非線性曲線族的平均曲線作為并聯阻尼力c.

3 動力學模型建立

通過建立車輛動力學模型，對時速400 km動車組在不同磨耗條件下的車輛動力學性能進行了計算仿真，部分動力學參數見表1，其余參數如下：車輛定距為17.8 m，軸距為2.5 m，車輪滾動圓橫向跨距為1.493 m，輪對內側距為1.353 m，車輪滾動圓直徑為0.92 m，車輪外形為LMB10，鋼軌外形為TB2344 60 kg鋼軌，軌距為1.435m，軌底坡1∶40，空簧橫向剛度為0.1～0.15MN/m，空簧橫向阻尼為10～20 kN·s/m.

鋼軌采用標準CN60鋼軌和CN60D標準打磨鋼軌.踏面類型選擇LMB_10新踏面和LMB_10磨耗后踏面.

仿真分析時，考慮比較惡劣的輪軌接觸關系，即等效錐度最低和最高兩種工況.仿真設置時，采用LMB_10新踏面與CN60D打磨鋼軌匹配來模擬等效錐度最低時的輪軌接觸關系，此時等效錐度為0.09.

表1 時速400 km動車組參數表

采用LMB_10磨耗后車輪踏面與標準CN60鋼軌匹配來模擬等效錐度最高時的輪軌接觸關系，此時等效錐度為0.45.線路設置為1 000 m直線軌道，分不施加激勵的簡單軌道以及施加武廣譜的有激勵一般軌道.

根據高速鐵路線路條件并參考武廣客專的線路幾何設置，對于300 km/h速度等級以上線路，其緩和曲線長度應大于300 m以保證其超高順坡率限值(1/10v)、超高時變率限度值的要求(25mm/s).

本次仿真中，8 000 m曲線對應超高160 mm，7 000 m曲線對應超高150 mm，5 500 m曲線對應140 mm，3 500 m曲線對應175 mm.動力學性能分析包括運行穩定性、運行平穩性和曲線通過安全性指標.

4 動力學模型驗證

對400 km/h高速列車，開展了線路動力學長期跟蹤測試，在機車車輛滾動振動試驗臺上開展了動力學試驗，獲得了大量的測試數據.圖4是采用隨機動力學仿真得到的橫向平穩性指標、垂向平穩性指標與線路測試、臺架試驗結果的對比.由于臺架試驗采用的軌道不平順樣本、輪軌接觸關系工況較少，所以平穩性指標變化范圍最小.隨機動力學仿真得到的平穩性指標變化范圍、平均值與線路長期測試結果基本吻合，平均值與臺架試驗結果接近.這證明了隨機動力學方法對高速列車動力學性能預測是比較可靠的.

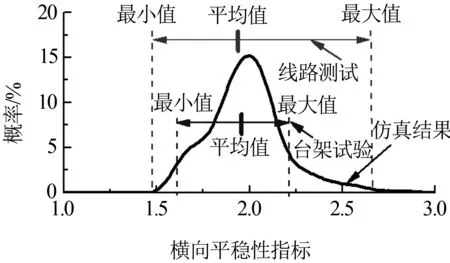
(a) 橫向平穩性指標驗證

(b) 垂向平穩性指標驗證

5 動力學性能計算

5.1 蛇行運動穩定性

運動穩定性分析采用的方法是對構架端部橫向加速度進行10 Hz低通濾波，分析構架端部橫向加速度最大值.對構架橫向加速度分析時，直接取濾波后最大加速度，沒有考慮峰值的次數，濾波范圍也比實際更寬，這是為了使分析結果更加安全，更具有工程意義.

從圖5可見，在400 km/h速度范圍內：

(1)LMB_10新踏面下，構架端部橫向加速度最大值(單峰值)均小于0.35 g；磨耗后踏面下，構架端部橫向加速度最大值(單峰值)均小于0.6 g.

(2)中間車輛構架端部橫向加速度最大值小于頭尾車輛.新輪狀態下，中間車輛構架端部橫向加速度最大值相較于頭尾車輛減小21%；磨耗輪狀態下，中間車輛構架端部橫向加速度最大值相較于頭尾車輛減小35%.

(a)新踏面

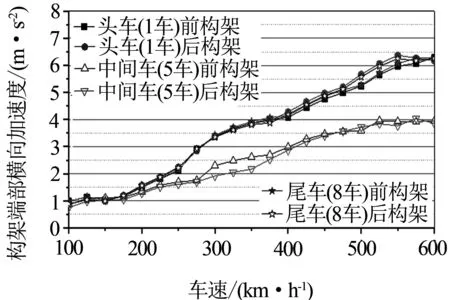
(b)磨耗后踏面

5.2 運行平穩性和舒適度

通過動力學仿真，分別計算各節車體前端、后端的橫向平穩性指標、垂向平穩性指標、舒適度指標.各種計算參數取名義值，變化計算車速.由于頭尾車及中間車輛的平穩性指標基本相同，故只使用頭車的平穩性指標進行繪制.

(a) 新踏面下的運行平穩性指標

(b) 磨耗后踏面下的運行平穩性指標

(a) 新踏面下的舒適度指標

(b) 磨耗踏面下的舒適度指標

從圖6和圖7可以看出：

(1)懸掛正常工況下，LMB_10新踏面、磨耗后踏面的橫向平穩性指標和垂向平穩性指標均小于2.5，舒適度指標均小于2.0.

(2)相較于新輪狀態，磨耗輪狀態下頭尾車輛以及中間車輛的舒適性指數值差異較小.

5.3 運行安全性分析

仿真分析動車組在LMB_10新踏面、磨耗后大錐度踏面下的動力學性能，分別計算車輛系統的輪軌作用力，并得到輪軸橫向力最大值、輪軌垂向力最大值、脫軌系數最大值、輪重減載率最大值.各種計算參數取名義值，變化計算車速.

從圖8可以看出，在400 km/h速度范圍內：

(1)輪軸橫向力、輪軌垂向力、脫軌系數、輪重減載率等各項安全性指標均滿足動力學標準要求，且有足夠的安全裕量.

(a) 輪軌垂向力

(b) 輪軌橫向力

(c) 輪重減載率

(d) 脫軌系數

(2)相較于頭尾車輛，中間車輛的相關指標數值較大.其中，輪軌垂向力增大13%.

(3)相較于新輪狀態，磨耗輪狀態下的輪軸橫向力、輪軌垂直力、脫軌系數和輪重減載率均有所增大.其中，輪軸橫向力增大45%.

6 結論

本文建立了8編組的時速400 km/h高速列車的多體系統動力學模型，分析了不同位置車輛之間、不同輪軌接觸關系下的車輛動力學性能差異，得出以下結論：

(1)高速動車組采用LMB_10踏面時，車輛的蛇行運動穩定性、運行平穩性和舒適性指標、運行安全性指標均能滿足相關標準要求，且有足夠的安全裕量，證明時速400 km/h高速動車組列車設計合理；

(2)新輪狀態與磨耗輪狀態相比較：在蛇行運動穩定性及列車運行安全性方面，新輪狀態的動力學性能均優于磨耗輪狀態；在列車運行平穩性和舒適性方面，兩者相關指標數值差異不大；

(3)中間車輛與頭尾車輛相比較：在蛇行運動穩定性方面，中間車輛動力學性能優于頭尾車輛；列車運行安全性方面，頭尾車輛的狀態要優于中間車輛的狀態；在列車運行平穩性和舒適性方面，二者相關指標數值差異不大.