基于CEEMD和快速譜峭度圖的地鐵軸箱軸承故障診斷
戎芳明,賈小平,楊陳
(中車浦鎮車輛有限公司 轉向架研發部,江蘇 南京 210000)*
轉向架軸箱軸承是影響城軌車輛的行車安全的重要部件,如何對其進行智能診斷是一個值得研究的課題.傳統頻域分析法主要是通過觀察頻譜圖中故障特征頻率處有無譜峰來診斷故障,診斷效率和精度都較低.近年來,隨著EMD、EEMD、VMD等理論在智能故障識別領域的應用,軸承故障診斷的手段進一步豐富.但EMD分解會出現模態混疊現象,EEMD可能會引入新的重構誤差,為避免EMD的模態混疊和EEMD重構誤差等問題,本文提出了基于CEEMD和快速譜峭度圖的故障診斷方法.通過仿真、試驗和工程實踐都表明,該方法有效識別出轉向架滾動軸承故障,為軸承故障診斷的智能化提供了新思路[1].
1 CEEMD-FSK算法基本原理
1.1 EMD、EEMD和CEEMD算法原理
經驗模態分解(Empirical Mode Decomposition),即EMD方法,是一種自適應的數據處理方法,使復雜信號分解成若干個本征模函數分量(IMF分量)來組成,但得到的IMF分量往往存在模態混合,建立式(1)仿真信號數學模型,如圖1可明顯可以看出IMF1中包含不同頻率分量[2].
(1)

圖1 EMD方法分解信號實例
為解決EMD分解出現的模態混疊現象,通過加入白噪聲,衍生出EEMD方法,而通過成對添加符號相反的白噪聲信號到原始信號,改進為CEEMD方法,其仿真時域波形處理步驟如圖2.

圖2 CEEMD方法的分解流程圖
1.2 快速譜峭度圖法與改進型共振解調法
1.2.1 快速譜峭度圖
譜峭度法(Spectral Kurtosis,SK),通過計算信號峭度值來指出隱藏的非平穩信號出現的頻帶范圍,本文采用二分法分解的快速譜峭度圖法以確定各IMF信號的帶通濾波頻率范圍.同時結合互相關系數的方式,有效選出關鍵IMF分量. 定義系統激勵信號x(t),其響應為Y(t),H(t,f)為Y(t)在頻率f處的復包絡.
(2)
譜峭度的定義為四階歸一化累積量,用式(3)表達:
(3)
其中,含噪聲的故障振動信號Z(t) 的譜峭度定義為:
(4)
式中,KY(f)為故障振動信號Y(t)的譜峭度,ρ(f)為信噪比的倒數.
1.2.2 改進型共振解調法
共振解調法,又稱包絡分析法,流程圖如下圖3所示.針對軸承振動信號,針對軸承振動信號,一般采取希爾伯特變換(Hilbert)進行求解,本文對比了傳統包絡譜、平方包絡譜和多次方包絡譜求解結果,結果表明采取平方包絡譜的方法更有利于特征信號的識別[1,3].
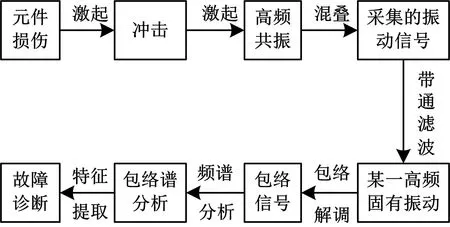
圖3 共振解調法的流程圖
1.2.3 CEEMD-FSK算法流程
原信號通過CEEMD分解成多個IMF,分別計算原始信號和各個IMF的快速譜峭度圖,從各個快速譜峭度圖中找出顏色最深的色塊,即譜峭度最大值區域,判斷各個IMF譜峭度最大值所處頻帶區間與原信號頻帶區間是否相一致,若一致,則初步認為則該IMF為關鍵IMF,否則去除.然后分別選取各IMF與原信號相關系數較大且其峭度值都大于3.5的前N階(N≤5)IMF信號,將選取的IMF進行信號重構.再對重構信號進行快速譜峭度分析,確定帶通濾波頻率范圍,然后通過改進型共振解調處理進行軸承故障診斷[4-6].將這種基于CEEMD和快速譜峭度圖(Fast Spectral Kurtosis Diagram,FSK)的方法稱為CEEMD-FSK算法,具體算法流程如圖4所示.

圖4 基于CEEMD-FSK算法的軸承故障診斷流程圖
2 仿真信號分析與對比
2.1 仿真信號模型的構建
為驗證本文方法的高效性,提出以下軸承故障信號仿真模型,假設如下:
(5)
其中,s(t)為周期性沖擊成分,幅值A0=0.5,轉頻fr=50 Hz,衰減系數C=900,共振頻率fn=3 500 Hz.內圈故障特征頻率fi=160 Hz,n1(t)和n2(t)為高斯白噪聲,其信噪比設置為-3.
圖5 基于EMD方法進行仿真模型故障診斷
EMD-包絡譜方法診斷結果如圖5,未找到軸承故障特征信號,可見該方法對復雜軸承故障信號診斷的有效性較低,需進一步優化.
2.2 CEEMD-FSK方法的故障特征診斷
使用CEEMD-FSK方法對仿真模型信號分析,由圖6可知,得共振頻率段范圍為(3 000 Hz,4500Hz),這是完全符合共振頻率fn=3 500 Hz的設置.由圖7可知,能夠診斷出基頻信號和內圈故障信號,很接近轉頻fr=50 Hz 和內圈故障特征頻率fi=160 Hz 的設置,由此可說明,CEEMD-FSK方法在復雜軸承信號下能高效檢測到軸承故障特征信息[7].
圖6 仿真模型信號的快速譜峭度圖

圖7 基于CEEMD-FSK方法的仿真模型故障特征診斷
3 振動測試分析和試驗對比
為驗證本文方法的有效性,將該方法用于某城軌車輛軸箱軸承的前期故障診斷中.
3.1 滾動軸承已知參數
軸承型號:BC2-0111;滾動體個數:16;滾動體直徑:27 mm;滾道節徑:167.5 mm;接觸角:0°;轉速為252 r/min(4.2 Hz)時對應車速40 km /h.
根據滾動軸承故障頻率的計算公式和實際滾動軸承參數,得各故障特征頻率分別為內圈:39.02Hz、;外圈:28.18 Hz;滾動體:25.38 Hz;保持架:1.76 Hz.
3.2 實測故障信號采集與分析
試驗主要儀器和傳感器如下:數據采集分析儀為INV3062T0;加速度傳感器(50g)為INV9832; DASP智能數據采集和信號分析系統V10為DASP-V10工程版平臺軟件;筆記本電腦Lenovo T440.
針對某地鐵車輛,在空車狀態下運行速度為40 km/h的某節車廂轉向架各軸箱軸承進行振動信號采集,采樣頻率設為19 692.3 Hz,車輛穩定運行狀態下采集時間長度為200 s,測點位置為各軸箱體正上方.
3.3 實測數據分析與拆裝檢測對比
3.3.1 信號的重構和故障診斷
通過快速譜峭度圖和相關系數綜合選擇出前5階IMF,具體排序見圖8.對信號進行重構,再次通過快速譜峭度圖,確定帶通濾波參數為(2000Hz,3 000 Hz).
圖8 選取前出前5階IMF作為重構信號
對重構信號進行帶通處理后,采用平方包絡譜方法進行共振解調,由圖9可知該軸承實際轉頻為4.66Hz,存在軸承內圈故障特征信號42.71Hz,而且出現了38.2 Hz的邊帶信號,對比各特征故障頻率,可診斷該軸承存在內圈故障.

圖9 基于CEEMD-FSK方法的軸箱軸承信號故障特征診斷
3.3.2 診斷結果與拆裝對比
為檢測CEEMD-FSK方法診斷結果的準確性, 將目標軸箱軸承拆裝送檢, 具體結果如圖10所示,對比圖9診斷結論,可以說明該方法的有效性和實用性.


圖10 故障軸承檢測示意測點及實際狀態
4 結論
本文基于CEEMD和快速譜峭度圖選取關鍵IMF分量進行信號重構,再通過快速譜峭度圖確定濾波頻帶,利用共振解調技術提取平方包絡譜判斷滾動軸承故障類型.該方法改進了傳統EMD-包絡譜方法的不足,提高了計算效率,診斷結果更精確,同時快速譜峭度圖克服了主觀上確定濾波參數的不確定性.仿真分析和試驗結果都表明了該方法能有效和正確地選擇敏感分量,提取到滾動軸承早期微弱故障特征信號,有效診斷出軸箱軸承故障類型.

