偏心槳機構水下旋轉槳式步態水動力建模

李小毛,彭 宇,李天波,陳俊杰,徐 佳,崔建祥

(上海大學機電工程與自動化學院,上海200444)

近年來,隨著機器人技術和相關理論的不斷發展,兩棲機器人逐漸成為國內外科研機構關注的熱點.兩棲機器人對于多種環境和地形介質具有良好的適應性,能夠協助或替代作業人員在惡劣多變的兩棲環境中執行各種危險、復雜的任務,在搶險救援、災后勘察和科學考察等領域具有廣泛的應用前景.

根據推進方式和系統方案的不同,可將現有的兩棲機器人分為2類:運動仿生型和融合推進型.運動仿生型兩棲機器人的機構和系統設計模仿了生物的運動特征和原理.Yang等[1]設計的FroBot機器蛙,通過一對仿蛙腳蹼的擺動鰭重現了青蛙的游泳方式;Yamada等[2]研制的蛇形兩棲機器人ACM-R5采用輪槳式推進機構作為關節模塊,可在水中和陸地上蜿蜒前進;Low等[3]研發的海龜機器人,通過模仿海龜鰭狀肢的形狀和運動方式設計類似的推進結構,實現了水陸兩棲作業;Jun等[4]研制了利用六足機構在海灘或海底步行的機器蟹CR200;此外,Crespi團隊[5]開發的Salamandra RoboticaⅡ機器人在仿生方面更進了一步,利用人工神經元模擬蠑螈脊髓神經中樞的功能,可根據地形變化自主選擇合適的爬行和游泳模式.融合推進型兩棲機器人則是通過整合或切換多種推進機構來實現高兩棲機動性能.Georgiades等[6]開發的Aqua機器人,通過更換剛性腿和柔性槳來實現兩棲運動;由Li等[7]設計的兩棲球形機器人,在水下采用噴射推進,陸上通過輪-腿復合機構移動;中科院Yu等[8]開發的機器人Amphibot-Ⅱ,獨創輪-槳-鰭融合式推進機構,依靠3種推進機構分工合作實現水陸兩棲能力;此外,Liu等[9]設計的自適應輪-腿式機器人,由大直徑輪腿復合機構驅動,能在不同環境下切換運動模式以提高運動效率.然而,由于機器人運動和適應能力的局限性,現有的兩棲機器人很難應用于海嘯、泥石流等災害發生后的復雜環境中.為了提高機器人在復雜兩棲環境下的通過能力,本工作設計了一種基于行星輪系和偏心槳(eccentric paddle,ePaddle)的復合型兩棲運動推進機構ePaddle[10].在前期研究中,通過設定不同機構的槳葉軸位置以及外輪旋轉模式,實現了輪式、腿式和輪腿融合式等陸上步態[11],以及旋轉槳式、擺動槳式水下步態[12-13],其中旋轉槳式步態下的機器人具有更高的巡航速度,適合在開闊水域航行.

構建合理準確的水動力學模型,對分析水下機器人的運動特性和制定控制策略具有重要意義.針對槳葉形狀、材料和運動方式的不同,研究人員提出了多種水動力學模型,其中剛性槳模型[14]和Lighthill模型[15]的應用較為廣泛.前者適用于同一水深下的槳葉推力預測,簡化了流體在不同深度產生的影響;后者雖適用于細長槳葉的擺動推力分析,但忽略了流體作用于槳葉的表面力.此外,Park等[16]提出了適用于柔性槳的偽剛體(pseudo-rigid-body,PRB)模型,將柔性槳簡化為通過鉸鏈和扭簧連接的剛體進行分析;王海龍[17]提出可通過求解Navier-Stokes方程分析機構水動力性能,但該方法在復雜流體環境中不能求得精確的數值解.

本工作通過構建ePaddle機構在水下以旋轉槳式步態運動過程中的水動力模型來分析其水下推力特性.首先,簡單介紹了ePaddle機構和旋轉槳式步態,并構建應用于水下旋轉槳式步態的推力預測模型;其次,在此基礎上進行了實驗驗證與討論;最后,進行總結并提出未來的研究規劃.

1 ePaddle機構與水下旋轉槳式步態

ePaddle概念由Sun等[18]首次提出(見圖1).ePaddle機構有3個自由度:獨立驅動的外輪殼體、兩自由度平面運動的槳葉軸和圍繞槳葉軸被動旋轉的槳葉.輪殼旋轉過程是通過調整槳軸的偏心距rS和偏心角θS,調節槳葉的姿態以及伸出輪殼外的長度來進行的.表1列出了其機構參數.

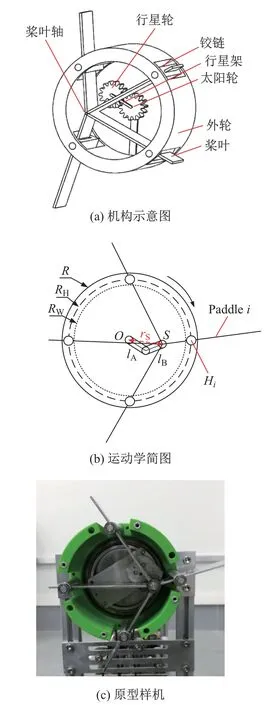
圖1 ePaddle機構Fig.1 Mechanism of ePaddle

表1 ePaddle模塊規格Table 1 Specifications of ePaddle module

ePaddle水下旋轉槳式步態如圖2所示,以外輪旋轉一周為一個步態周期.在初始狀態下,槳葉軸S被置于相對于外輪中心軸O的偏心位置.當外輪繞中心O沿固定方向旋轉時,輪殼帶動4個槳葉繞槳葉軸S旋轉產生推力,進而推動機構在水中向前運動.通過調節槳葉軸相對于輪心的位置,可以改變外輪旋轉過程中4個槳葉伸出外輪接觸水體的長度和面積,進而控制機構產生推力的大小和方向.

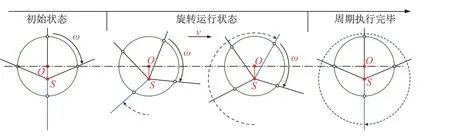
圖2 旋轉槳式步態相序Fig.2 Rotational paddling gait sequence

類似地面上輪胎的打滑現象,ePaddle機構水下運動時也會發生“打滑”現象,參考輪式移動機器人使用的滑差率定義,機構水下打滑程度可由滑差率s表示:

式中:v為機構水下水平運動速度;R為外輪半徑;ω為外輪轉速.

2 旋轉槳式步態動力學模型

本工作基于文獻[19-20]中提出的方法,使用Morison方程構建ePaddle機構的推力預測模型,其坐標系如圖3所示.ePaddle機構在執行旋轉槳式步態時會產生水波,其波長遠大于機構槳葉截面等效直徑,故適用Morison方程.本工作作如下簡化假設:

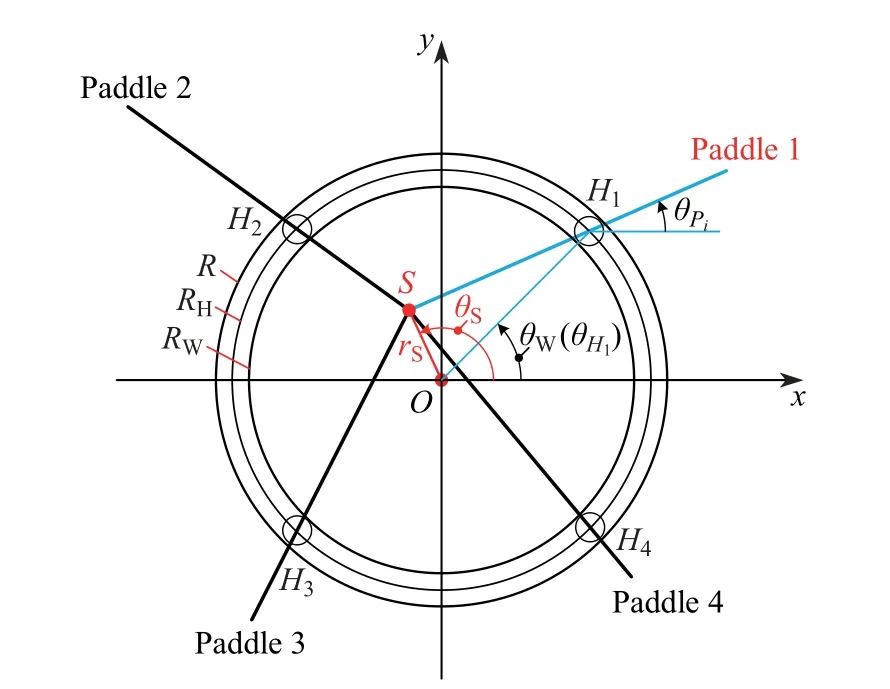
圖3 ePaddle機構坐標系Fig.3 Coordinate system for ePaddle mechanism

(1)假設流體為無旋且不可壓縮的黏性流體;

(2)根據運動的相對性,機構在水下以一定速度水平勻速運動,轉化為水流以大小相同、方向相反的速度流過固定位置上的機構,機構執行旋轉槳式步態產生的微小流速變化相對于水流速度可忽略不計;

(3)機構運行時輪內槳葉與流體的作用可忽略不計.機構運動時受到的流體力FS為外輪-流體之間的作用力FW,與槳葉伸出外輪部分產生的有效推力F的矢量疊加,即

為探究機構旋轉槳式步態的動力學特性,本工作主要研究機構執行旋轉槳式步態時產生的有效推力F(文中所指推力全部為有效推力F).

圖4為槳葉受力分析及坐標系定義.圖4(a)中,以外輪輪心O為原點建立慣性坐標系{xglobal,yglobal,zglobal},槳葉寬度為B;槳葉長度為L;厚度為A;=[Vx,Vz]T是慣性坐標系下的水流速度.由假設(2)及式(1)可知

當外輪轉速不變時,水平流速大小僅與滑差率s有關,且s越大水平流速越小.

以槳軸中心S為原點,在槳葉i上建立槳葉坐標系,其中x軸沿槳葉方向向外,z軸方向垂直于槳葉.從慣性坐標系轉換到槳葉坐標系的旋轉變換矩陣為

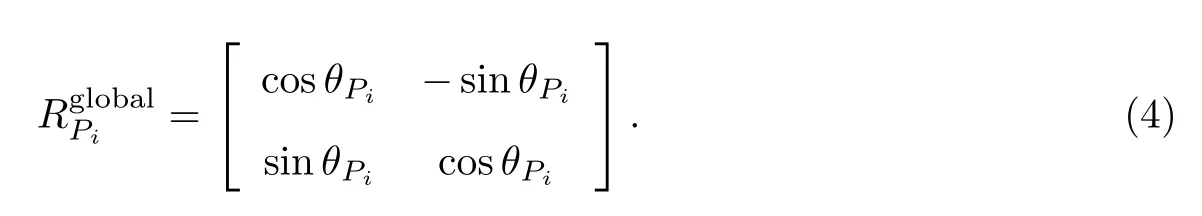
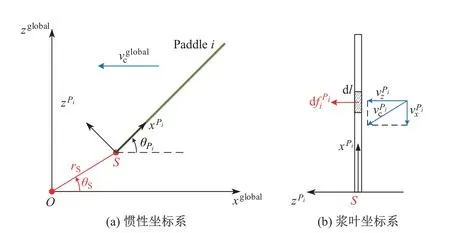
圖4 槳葉受力分析及坐標系定義Fig.4 Schematic of thrust analysis on a paddle and coordinate system

圖4(b)中,在槳葉坐標系中采用微元法對一小段槳葉dl進行水動力求取,求得水平流速在槳葉坐標系下的速度:

參考文獻[19],利用Morison方程變形式求出在槳葉坐標系下微元dl所受水動力:

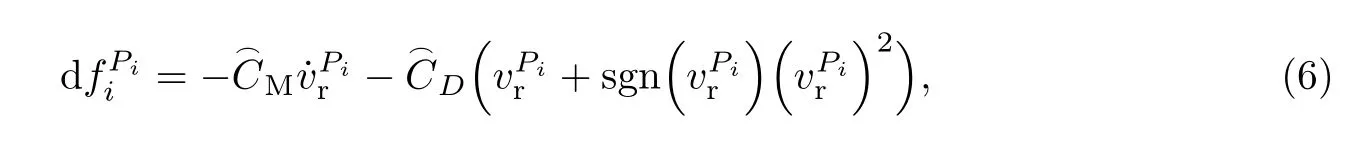
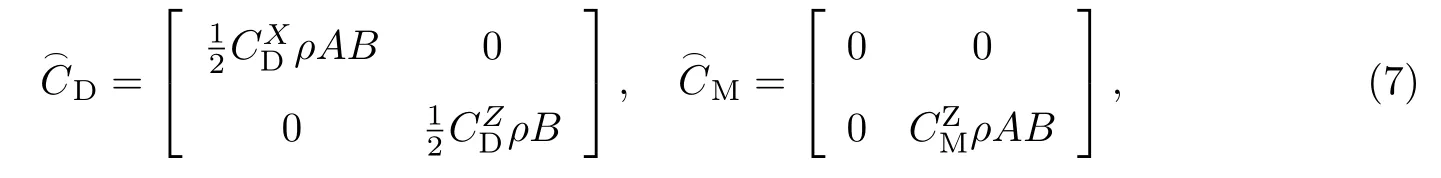
式中:ρ為水的密度;和分別為槳葉坐標系下x和z方向的繞流拖曳力系數;是z方向上的附加質量系數.由于槳葉為細長體,故x方向上的附加質量系數可忽略不計.實驗環境中雷諾數Re為105級別,據此系數經驗值[21]取.

由式(6)得到受力微元dl所受水動力,通過沿伸出外輪的槳葉長度進行積分可求得在槳葉坐標系下伸出外輪槳葉部分產生的推力:

由運動學分析可得第i個槳葉伸出外輪的槳葉長度

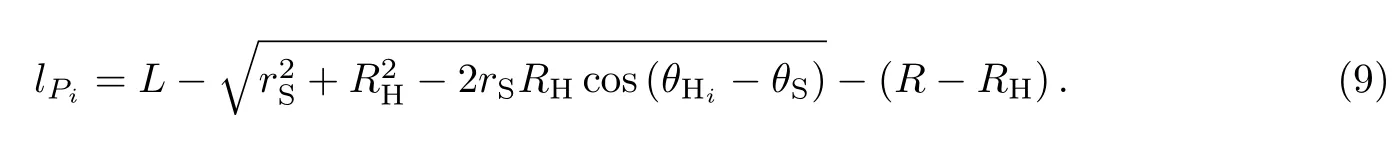
將槳葉坐標系下的推力旋轉變換到慣性坐標系下,即可求得單個槳葉i在某一時刻的推力

進而求得一個ePaddle機構4個槳葉產生的推力:

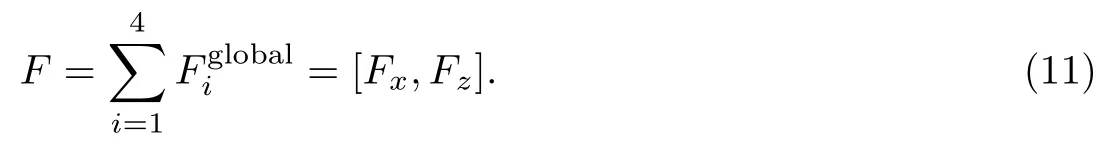
3 水下推力測試實驗

3.1 實驗設置

本工作設計了3組實驗,分別驗證在旋轉槳式步態下,不同槳軸偏心角θS、槳軸偏心距rS和外輪轉速下滑差率s對ePaddle機構水下推力特性的影響,實驗參數如表2～4所示.為保證實驗的準確性和可重復性,每組實驗重復10次取平均值作為實驗結果,同時使用離散小波變換(6層db6小波)濾除實驗臺機架振動、白噪聲等引起的噪聲干擾,提取原始推力信號.為分析在不同滑差率下由槳葉產生的推力,最終實驗結果設為傳感器測得機構產生的推力減去相同實驗參數下零槳配置機構產生的阻力得到的凈推力.

表2 2種槳軸偏心角下滑差率影響推力特性的實驗參數Table 2 Experimental parameters for identifying effects of slip ratio in two different eccentric angles

表3 不同槳軸偏心距下滑差率影響推力特性的實驗參數Table 3 Experimental parameters for identifying effects of slip ratio in different eccentric distances

表4 不同外輪轉速下滑差率影響推力特性的實驗參數Table 4 Experimental parameters for identifying effects of slip ratio in different rotational speeds

3.2 力學測試平臺

本工作在2.3 m×1.8 m×1.7 m尺寸的水箱內搭建了力學測試平臺(見圖5),測量ePaddle機構在執行水下旋轉步態時所受的水動力.ePaddle機構安裝在支撐平臺上,可通過導軌和直流伺服電機驅動滾珠絲杠(BSSR2505-1420,MiSUMi)帶動ePaddle機構實現水平移動.ePaddle機構和支撐平臺間固連有一個6軸力傳感器(F/T Delta SI-330-30),用于測量ePaddle機構在實驗時所受到的水動力.在實驗過程中,整個ePaddle機構完全浸沒在水中,由3個直流電機(RE30,Maxon motor)通過同步帶輪驅動.3個電機裝有減速器和增量式編碼器,由Copley ACJ-055-09驅動器分別驅動,通過CANopen通訊協議由NI PXI-1042Q控制箱控制.控制箱接入的數據采集卡以1 000 Hz的采樣頻率對力傳感器以及編碼器反饋的數據進行實時采集,所有控制和數據采集程序在Labview軟件環境運行.

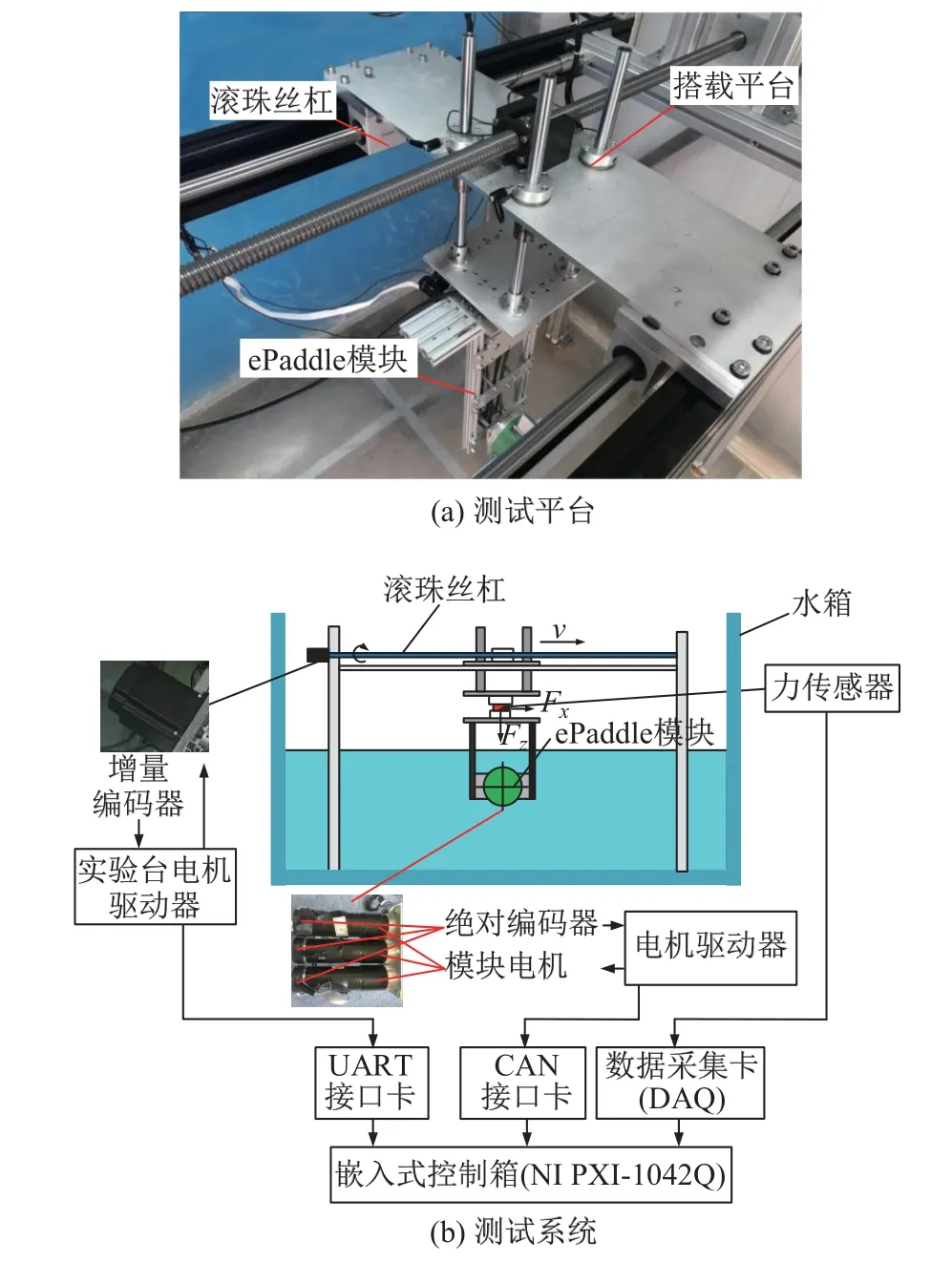
圖5 力學測試平臺Fig.5 Mechanical test platform

3.3 實驗結果

不同實驗參數下測得的結果與由Matlab仿真得到的預測結果對比情況如圖6～10所示(圖中實線為實驗值,虛線為理論值).從圖中可以看出,機構產生的瞬時推力實驗值均呈類正弦曲線形態,一個旋轉周期內有4個波峰和波谷,3組實驗結果的對比驗證了推力預測模型的準確性.當外輪轉速增大時,z方向上的實驗結果與預測結果偏離較大,估計是由于高外輪轉速產生了更大的水波,從水箱壁上反彈的回波作用于槳葉造成了水動力的耦合.

(1)不同槳軸偏心角下滑差率對機構推力的影響.圖6為2種槳軸偏心角配置下不同滑差率產生的推力對比結果.圖中,隨著滑差率變大,機構產生的水平推力顯著減小,而豎直推力值差別較小.當滑差率小于0.9時,2種槳軸偏心角下的機構均可在水平方向上產生正向推力,推動機構前進.此外,在槳軸偏心角為-90?時,水平推力整體大于偏心角為0?時產生的水平推力,但此時在豎直方向上產生了更大的下沉力.

(2)不同槳軸偏心距下滑差率對機構推力的影響.圖7為槳軸偏心距為30 mm時機構在不同滑差率下產生的推力對比結果.隨著滑差率增大,機構的水平推力顯著減小.通過圖8中不同槳軸偏心距下峰值推力的對比可以發現,隨著槳軸偏心距的增大,槳葉會產生更大的峰值推力,且隨著滑差率增大,水平峰值推力呈線性減小的趨勢,而豎直峰值推力的變化較小.與圖6進行對比可知,槳軸偏心距增大,機構在相同轉速下能在一個周期內更快達到峰值推力,此時瞬時推力曲線的幅值會顯著增大,特別是在豎直方向上.

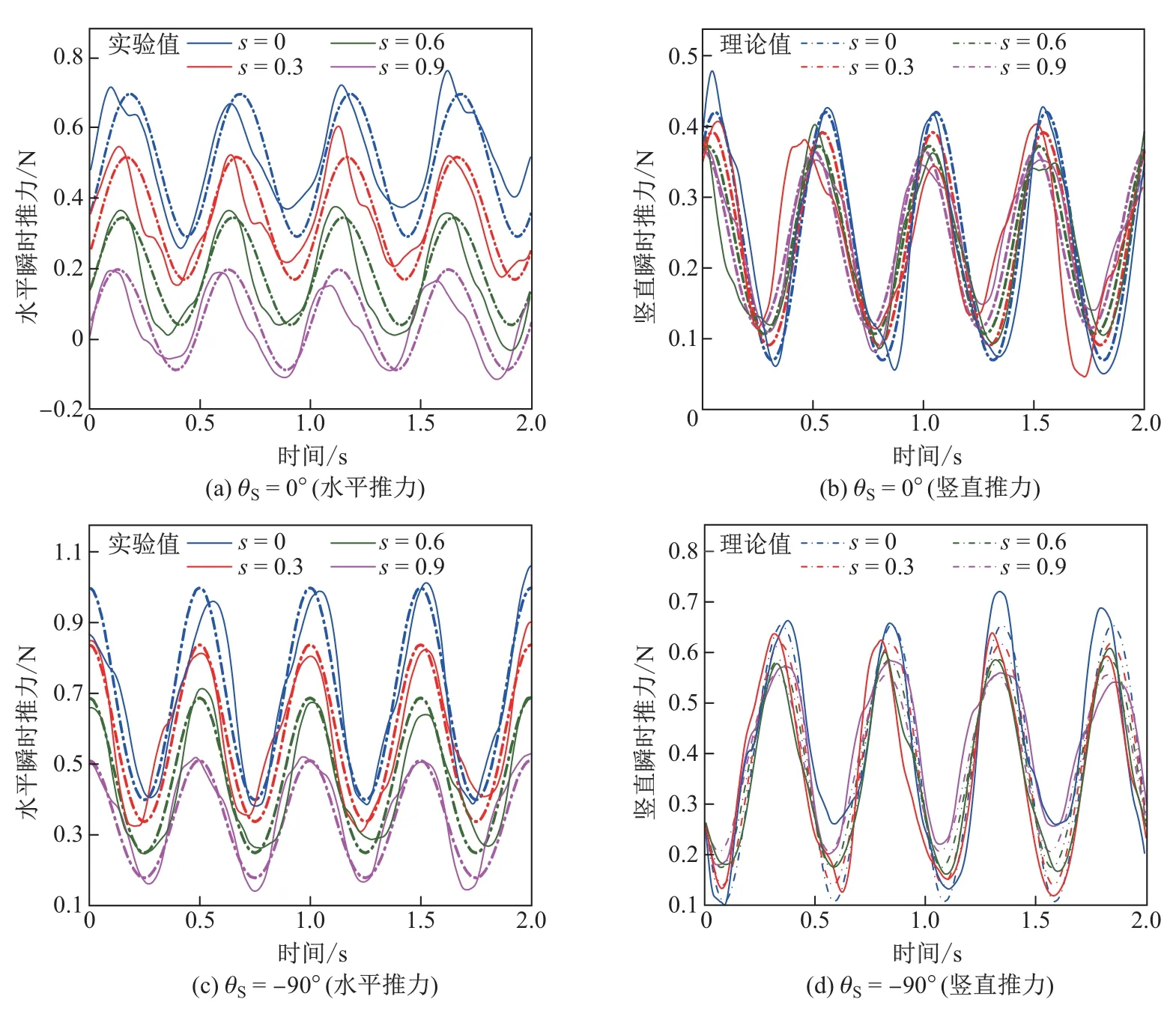
圖6 2種槳軸偏心角配置下不同滑差率產生的推力對比Fig.6 Thrusts in x-and z-axis direactions with differentθS in different slip ratios

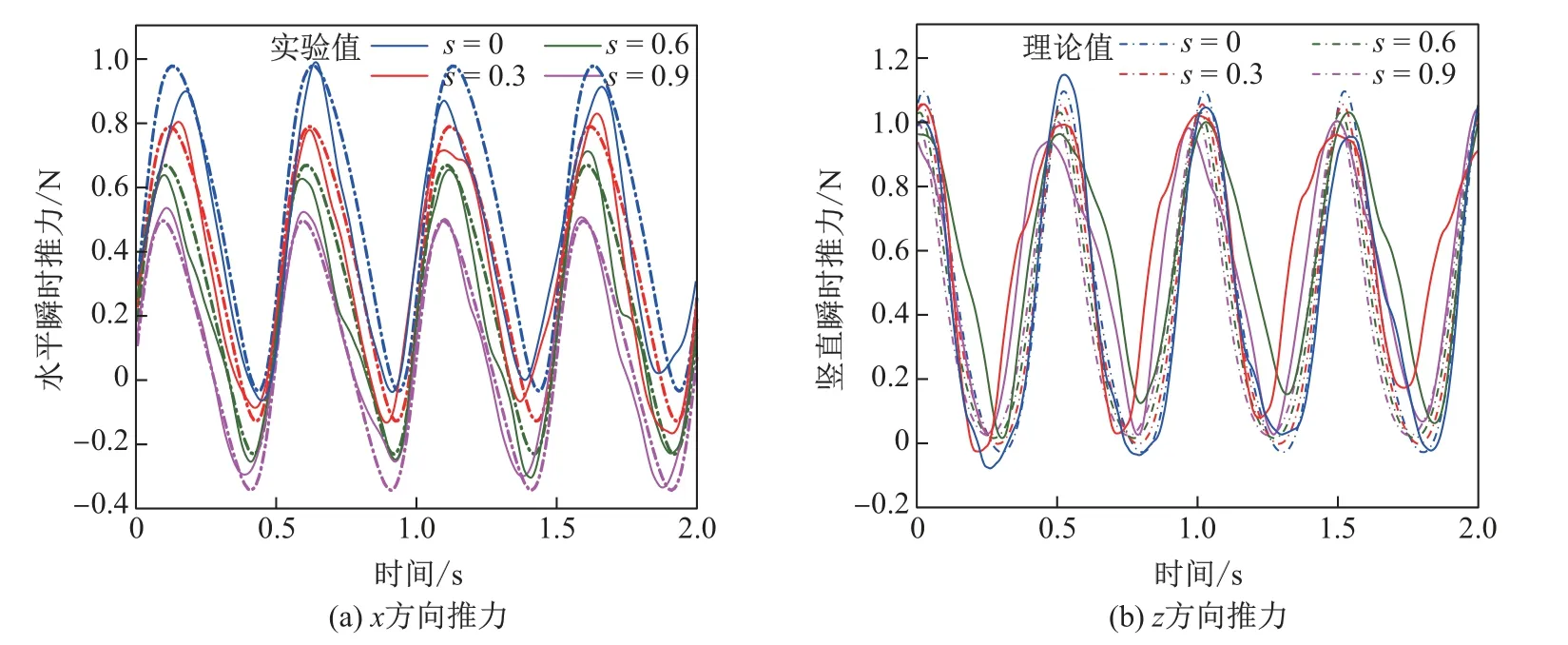
圖7 槳軸偏心距為30 mm時滑差率變化產生的推力對比Fig.7 Thrusts with 30 mm eccentric distance in different slip ratios

(3)不同外輪轉速下滑差率對機構推力的影響.圖9為機構在外輪轉速為60 r/min時不同滑差率下產生的瞬時推力的對比結果.隨著滑差率的增大,機構在水平方向上產生的推力值顯著減小.與外輪轉速為30 r/min時測得的實驗結果相比,瞬時推力值提高了2倍以上.圖10為機構在不同外輪轉速下滑差率變化產生的平均推力圖.從圖10可以看出,隨著外輪轉速的提高,槳葉產生的平均推力值顯著增大,且隨著滑差率的增大,水平方向上的平均推力值線性減小,而豎直方向上的平均推力基本保持不變.

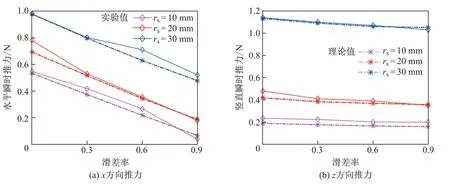
圖8 不同槳軸偏心距下滑差率變化產生峰值推力對比Fig.8 Peak thrusts with different eccentric distances in different slip ratios

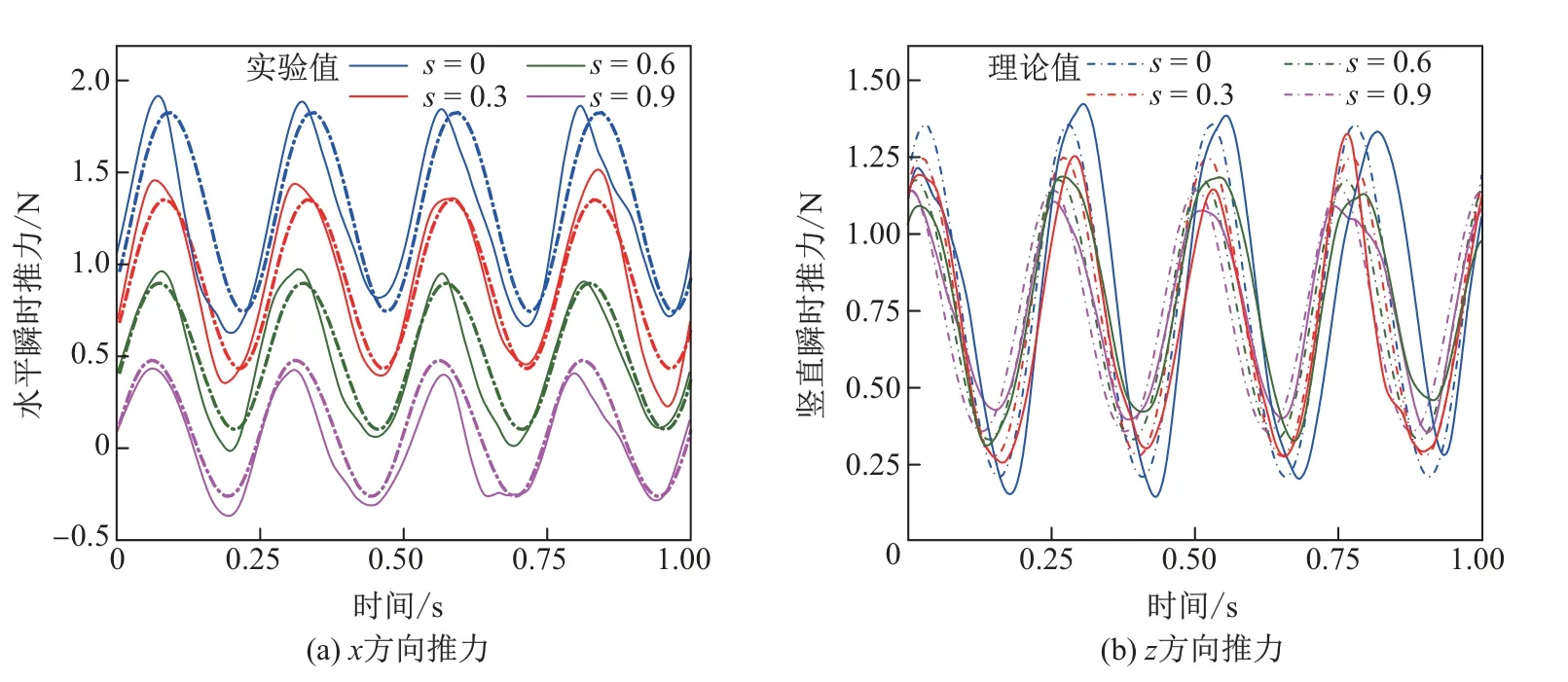
圖9 外輪轉速為60 r/min時滑差率變化產生的推力對比Fig.9 Thrusts with 60 r/min rotational speed in different slip ratios

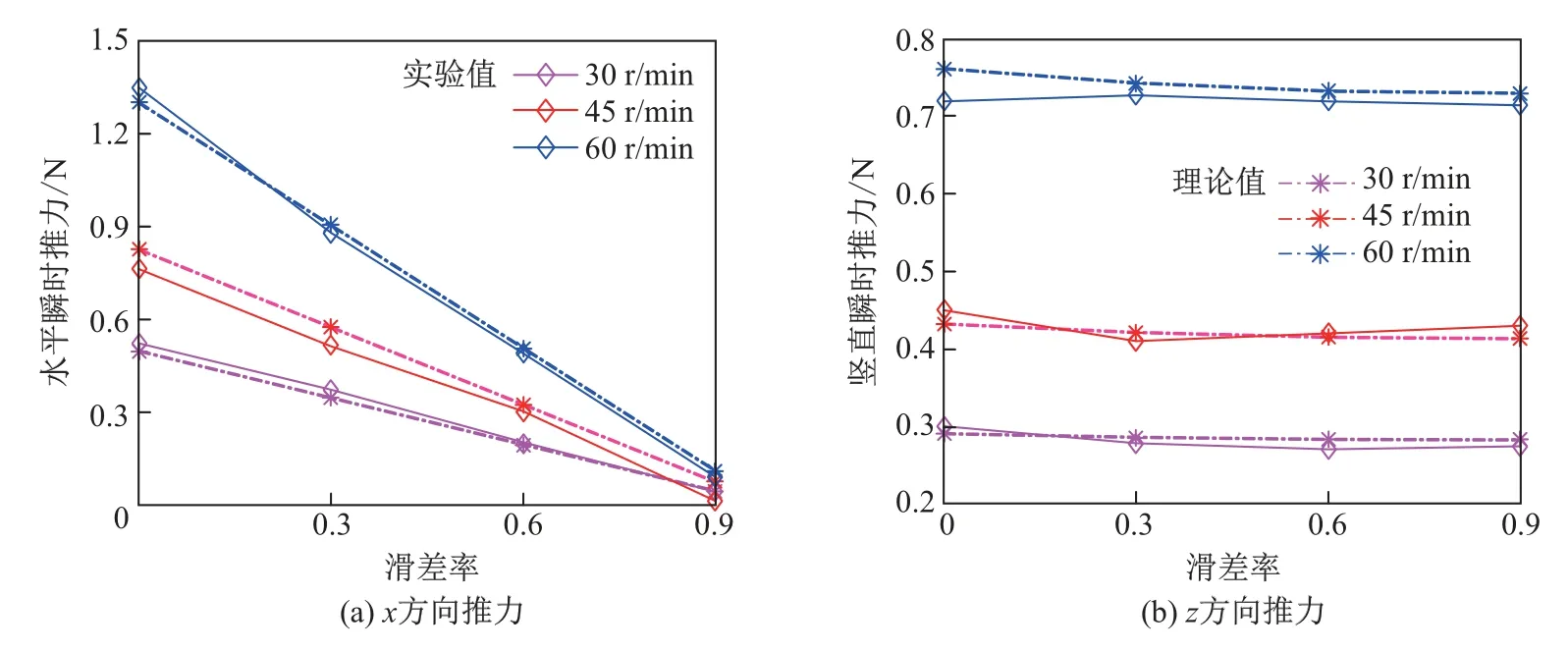
圖10 不同外輪轉速下滑差率變化產生的平均推力對比Fig.10 Average thrusts with different rotational speeds in different slip ratios

3.4 討論

通過上述實驗結果可知,不同運動配置參數下的機構在執行旋轉槳式步態時,產生的水平推力隨著滑差率s的增大而減小,而豎直推力受滑擦率影響較小.由式(3)可知,當滑差率s增大時,水流的水平流速Vx減小,槳葉相對于水流的速度也相應減小,而槳葉所受到的水動力與槳葉相對于水流的速度成正比(見式(6)).因此,可通過減小ePaddle機構運動的滑差率來提高推進效果,同時保持機構理想的運行狀態.

不同槳軸偏心角配置下的推力實驗結果表明,在合適的滑差率下(s＜0.9),2種配置下的機構執行旋轉槳式步態時均可在前進方向上做正功,即在保證較高的運動速度的同時,產生較為理想的推進力.偏心角為-90?配置下的機構能產生更大的正向推力,可高效推進機構前進,實現更快的加速度和巡航速度.針對機構在運行過程中產生豎直下沉力的問題,可以通過加裝浮力材料來抵消其影響.

對于不同槳軸偏心距配置下推力的實驗結果表明,增大偏心距會產生更大的峰值推力.通過式(8)、(9)可知,當槳軸偏心距rS增大時,一個周期內伸出外輪的最大槳葉長度lPi,max會增大,增大了水流作用于槳葉上的面積,從而可以產生更大的峰值推力,同時槳葉伸出長度的變化幅度也會增大,使推力幅值變大.大槳軸偏心距下機構可以更快地達到峰值推力,但在豎直方向上會引起明顯的推力波動,說明較大的槳軸偏心距會破壞機構在豎直方向上的運動穩定性.

4 結束語

本工作構建了ePaddle機構執行旋轉槳式步態時的推力預測模型,分析了不同配置參數對機構推力特性的影響,并通過實驗驗證了該模型的準確性,為制定機器人運動控制策略提供了理論基礎.結果表明,機構水平推力隨滑差率的增大而減小;-90?槳軸偏心角的配置可提供更大的前進推力,更適合實際應用;增大槳軸偏心距可增大機構的峰值推力,而提高外輪轉速可明顯增大平均推力和提高推進效率.在未來工作中,將基于本工作的結論,研究采用多個機構的兩棲機器人執行旋轉槳步態時的步態規劃與協調控制問題.