大氣浮力頻率的時空變化及其影響因子

楊可心,陸爾,趙瑋

摘要 采用NCEP/NCAR再分析資料，分別將一日4次、日平均、月平均資料作為輸入進行計算，分析了浮力頻率在不同尺度下的時間變化及空間變化，發現浮力頻率的分布與緯度和高度、海洋和陸地、山脈和地形分布等有關。一般認為，浮力頻率取決于上下層的溫度差。通過對其表達式的推演，指出浮力頻率除了與上下層溫度差有關外，也與氣溫本身有關，是兩者的非線性函數。針對不同時間尺度及空間的采樣樣本，研究了氣溫和垂直溫差在浮力頻率時空變化中的相對重要性。結果表明，對浮力頻率的某些時空變化，在一些區域，氣溫本身的變化也很重要，其影響甚至能超過上下層溫度差的作用。

關鍵詞 浮力頻率;時空變化;氣溫;溫度垂直差異;相對重要性

對大尺度、平均狀態而言，大氣在垂直方向上可認為是靜力平衡的。實際大氣中會有區域性的不穩定對流活動。在穩定大氣中，因靜力平衡作用，大氣能在垂直方向上形成振蕩、并以重力波的形式向周邊地區傳播。這種波的活動對臨近地區的天氣會有影響，在條件不穩定大氣中可觸發暴雨（李麥村，1978;朱莉等，2010;王文等，2011;舒斯等，2015）。

重力波的形成和傳播與靜力穩定程度有密切關系，大氣浮力振蕩頻率正是用來定量描述這種穩定程度的。李麥村（1978）從大氣運動和熱力學方程組出發，建立了有關垂直運動的理論方程，由此進行了重力波的解析分析。他的研究指出，重力波的波速是與浮力振蕩頻率相關聯的。通過對湖北地區一次特大暴雨的個例研究，發現該次暴雨的移速與重力波的波速相符，浮力頻率是這次降水過程的一個重要影響因子。

早在90年前，芬蘭的維薩拉和英國的布倫特分別對大氣的浮力振蕩進行了研究（Vaisala，1925;Brunt，1927）。通過分析氣塊在垂直方向上受到輕微擾動后的受力和加速度，他們給出了波動方程并探討了其頻率項的物理意義，該項也就是所謂的浮力頻率（N），指的是大氣中氣塊圍繞平衡位置做絕熱浮力振蕩時的頻率。在相關教科書中一直沿用他們經典的方法及計算。通常將數值取成一個常數，如在《動力氣象學》（呂美仲等，2004）中，給出的N的數值是1.2×10-2 s-1。

在這一概念提出后的幾十年里，學者們對浮力頻率進行了若干方面的研究。針對海洋中的浮力頻率，蔡樹群等（1997）將3次樣條插值法應用于海洋浮力頻率的計算中;蒲書箴等（2004）揭示了海洋浮力頻率的分布特征、年際變化、及與ENSO和La Nia現象之間的關聯;Haren（2005）研究了海洋波導中的內波與浮力頻率;方長芳（2010）指出在全球變暖過程中，上下層海水增暖幅度差異會使海洋浮力頻率變高，從而影響海洋Rossby波的傳播。

在大氣浮力頻率方面，林本達和高山月（1994）指出中等大小的浮力頻率值最有利于行星波的垂直傳播;劉棟與高守亭（2003）研究了飽和大氣中凝結的液態水從氣塊中的分離，對飽和濕大氣浮力頻率的表達式進行了修正;陳權亮等（2005）著眼于平流層的浮力頻率，研究了其水平分布和垂直特征;Angell et al.（1969）討論了行星邊界層中的浮力頻率濤動;McHugh（2015）發現對流層頂的浮力頻率突變會影響重力內波及與此相聯系的大氣環流。

先前的這些研究，大多或著眼于海洋或平流層，對整個大氣層的浮力頻率的研究相對較少，特別是針對不同時間尺度的分析。本文旨在弄清在不同時間尺度上，浮力頻率在整個大氣層中的三維結構和時間演變;并從理論上進行一些探討，以理解浮力頻率對其影響因子的依賴關系。用再分析資料進行計算，分析浮力頻率日內變化、逐日變化、及季節變化的特征。根據推導，浮力頻率可表達為氣溫及上下層溫度差的函數，用基于回歸的方法研究這兩個影響因子在浮力頻率變化中的相對重要性。

1 方法和資料

進行浮力頻率推導時，通常采用的是小擾動法。在靜力平衡的環境中，當氣塊受到擾動后，最初的平衡態被破壞，重力與浮力不平衡，因而產生了垂直方向的加速度，由原本的高度位移一小段距離δz，到達了新的位置，由此建立了運動方程。發生移動后，氣塊的密度與氣壓實際上都發生了改變，既不是初始狀態，也來不及變化到環境的狀態。在此假設氣壓能夠立即適應環境，并且氣塊溫度是根據干絕熱遞減率變化的。通過代入理想氣體狀態方程和靜力平衡方程，對運動方程進行變換，得出下列波動方程：

d2δzdt2+gθθzδz=0。? （1）

由此得出N2的定義表達式：

N2=glnθz。? （2）

為了方便地應用再分析資料，根據位溫的表達式，經推演得到：

N2=g2cpT-pg2TRT2p。? （3）

將上式寫成差分的形式，可得如下形式：

N2=g2cp·1T·1-K·1T·ΔT。? （4）

其中：K=cp/R·p/Δp。對兩個相鄰等壓面之間的各層進行計算。各層的溫度和氣壓取成上下兩個等壓面上的平均值。因此，各層的浮力頻率可由上下等壓面的平均溫度和溫度差決定。CAM5模式（Eaton，2016）中也給出了相似的表達式。

采用NCEP/NCAR再分析（Kalnay et al.，1996）中的溫度資料，水平分辨率為2.5°×2.5°。針對不同時間尺度，分別選用2017年的、及1948—2017年的資料。

2 不同時間尺度浮力頻率變化的特征

2.1 浮力頻率的日內變化

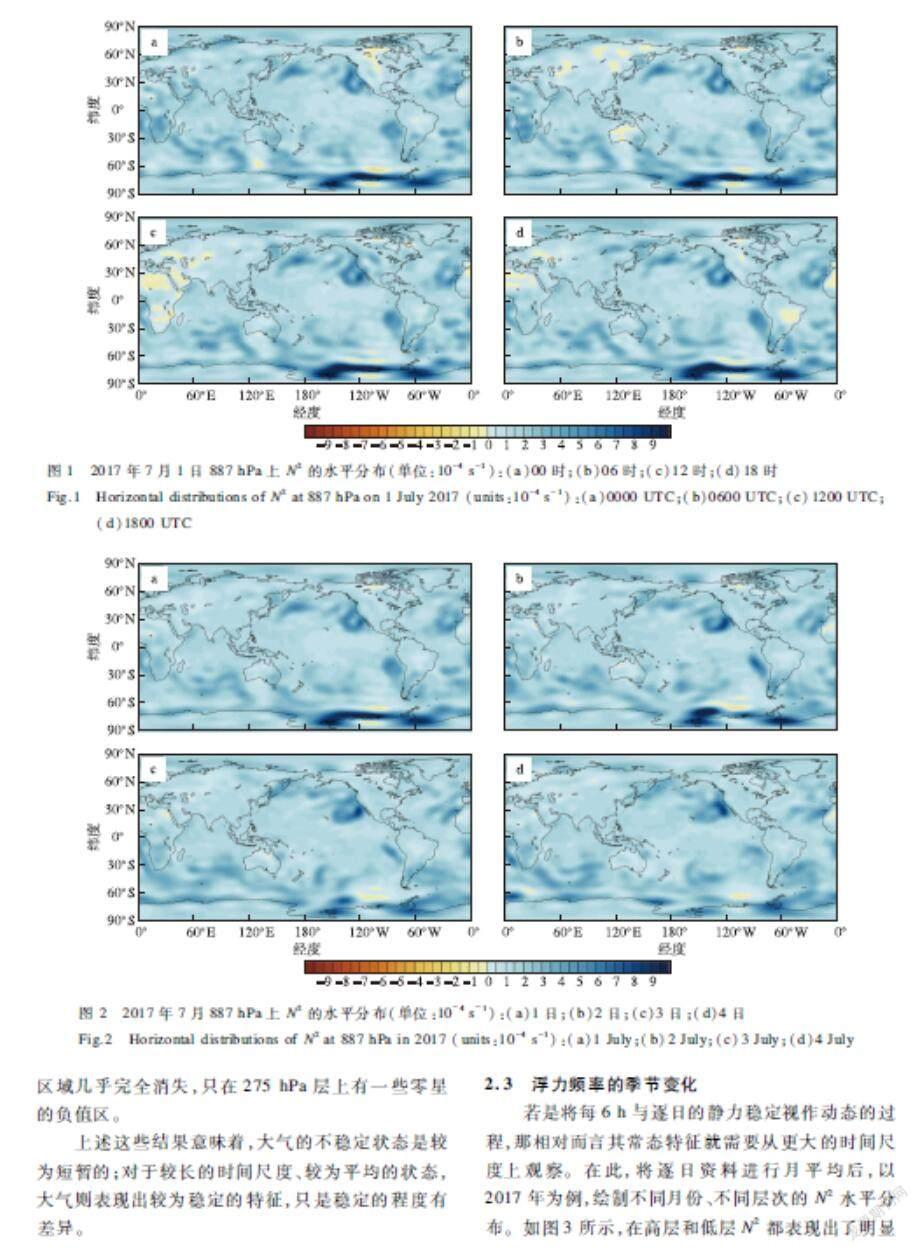
圖1是2017年7月1日4個時次850～925 hPa層（記為887 hPa層，下同）的N2的水平分布。圖1中黃色區域代表此地的N2為負值，因而大氣處于靜力不穩定的狀態;深藍色表示該處N2為較高的正值，因而大氣是層結穩定的。可以看到，黃色負值區域存在明顯的日變化。因N2是平均溫度與溫度差的函數，所以某一格點的靜力穩定度在一天之中發生較大的變化是有可能的，特別是黃色負值區和淺藍色正值區的交替出現，代表著此處的大氣在不穩定和穩定之間反復變化。

在這4個時次中，陸地上空負值區的出現并不連貫，00時（世界時，下同）主要位于北美洲，北非和熱帶南美洲局部也有分布;06時主要出現在亞歐大陸中緯度區域和澳洲;12時在非洲南部與北部、阿拉伯半島和哈薩克斯坦一帶;18時位于非洲西北部和南美洲東部。在后三個時次里，北美洲局部仍然有小范圍的不穩定區。南極大陸瑪麗博德地-阿蒙森海一帶出現了負-正-負的浮力頻率分布情況。

然而在每天的同一時次，這些負值區的出現位置較為固定。繪制更多層次后發現，通過每6 h的溫度資料計算出的7月的N2在125 hPa以下各層均有負值區域出現，平流層大氣中也會出現不穩定的區域。

2.2 浮力頻率的逐日變化

雖然日內的靜力不穩定區域位置跳躍較大，但其逐日變化卻很有規律。以2017年7月1—4日為例，圖2是887 hPa層N2的水平分布，可以看到，該層的N2空間上差異較大，海洋和陸地上空大多為淺藍色，穩定度較低;深色高值區主要位于北太平洋、大西洋沿岸、和南半球中緯度西風帶上。四天的過程中，這些高值區的位置和強度都在不停地發生變化，但大多貼著海岸線移動。黃色負值區位于加拿大以北、撒哈拉沙漠周圍和西南極洲的阿蒙森海，四天中有一些位置上的飄移。

大氣靜力穩定度分布的時間演變，有相對穩定的一面，這可能與海陸和地形等有關;它也有移動和變化的一面，這可能是因受到大氣環流的影響。

繪制了不同層上的靜力穩定度N2的分布（圖略）。在7月1—4日的450 hPa以上的各層，負值區域幾乎完全消失，只在275 hPa層上有一些零星的負值區。

上述這些結果意味著，大氣的不穩定狀態是較為短暫的;對于較長的時間尺度、較為平均的狀態，大氣則表現出較為穩定的特征，只是穩定的程度有差異。

2.3 浮力頻率的季節變化

若是將每6 h與逐日的靜力穩定視作動態的過程，那相對而言其常態特征就需要從更大的時間尺度上觀察。在此，將逐日資料進行月平均后，以2017年為例，繪制不同月份、不同層次的N2水平分布。如圖3所示，在高層和低層N2都表現出了明顯的海陸分布特性，并且高層的N2分布還與大地形有一定聯系。

由圖3a、b可以看出，1月的15 hPa層上，更大的靜力穩定度出現在北極的格陵蘭島、喀拉海、西伯利亞和東非、南非高原，而中高緯度的北太平洋一帶則是N2的相對低值區;在美洲大陸上空，高值的靜力穩定度沿海岸線分布在陸地一側，恰好對應著科迪勒拉山系、安第斯山系和巴西高原。而在7月的同一層次上，高值伴隨著一個減弱的低值中心出現在南極，美洲山脈附近的高值區域依然存在，強度上有所減弱。綜合兩圖可以看出，中低緯度地區N2大致呈現赤道向兩極遞減的趨勢，極地的高值帶總是出現在冬半球，高原或山脈上空的值總是較大。

上述15 hPa反映的是平流層的穩定度分布，對流層的情況可用887 hPa層進行研究。如圖3c、d所示，1月的高值區仍然在北極，但大范圍的低值中心已不再存在，中低緯度的分布較為平均，7月時南極的高值區域從南極大陸移動到了海上。另外，在大陸西側的海洋上，兩季節均出現了一些靜力穩定度高于周圍的區域。1月時，位于南半球的這些高值區域強度要高于位于北半球的區域，而7月則正好相反，即夏季半球的值強于冬半球的值。與15 hPa層相比，887 hPa層上N2的高值更高，低值更低，差異更為明顯。

在其他一些層上，N2的分布也存在不同程度的海陸差異和地形特征。例如25 hPa層上中緯度的分布情況幾乎與15 hPa層完全不同，非洲東南部高原與美洲山脈附近的N2都從高值轉變成了低值中心，南北極卻與上層情況較為相似。775 hPa層上則在非洲大陸與澳大利亞上空出現低值區，形狀與陸地吻合。但中間大氣650～40 hPa上呈現出的主要是隨緯度的變化，與海陸沒有明顯關系。其中85 hPa以上層的N2值在中低緯度高于兩極，而85 hPa以下層，N2近似是由赤道向兩極遞增。

為了更清楚地理解浮力頻率的垂直分布情況，對緯向平均的N2做經向垂直剖面（圖4），可以看出，對流層赤道上空及中緯度地區的數值較小，1—7月的差異不大，符合其對流旺盛、靜力穩定度低的特征;400 hPa以上大氣里，中低緯地區在300 hPa有極小值中心，在50 hPa有極大值中心，縱向看，對流層頂處等值線密集，平流層的N2急劇增高;橫向觀察，則同一等壓面上的N2近似向兩極遞增或遞減。此外，兩個月份的低層大氣中，分別在北極與南極出現了極大值中心，其中1月北極的高值中心位于地面，7月南極的高值中心則大致在750 hPa，后者強于前者。與對流層低層高值中心相呼應的是，在平流層中高層也出現了相應的高中心。

3 浮力頻率變化中溫度和溫差的相對重要性分析

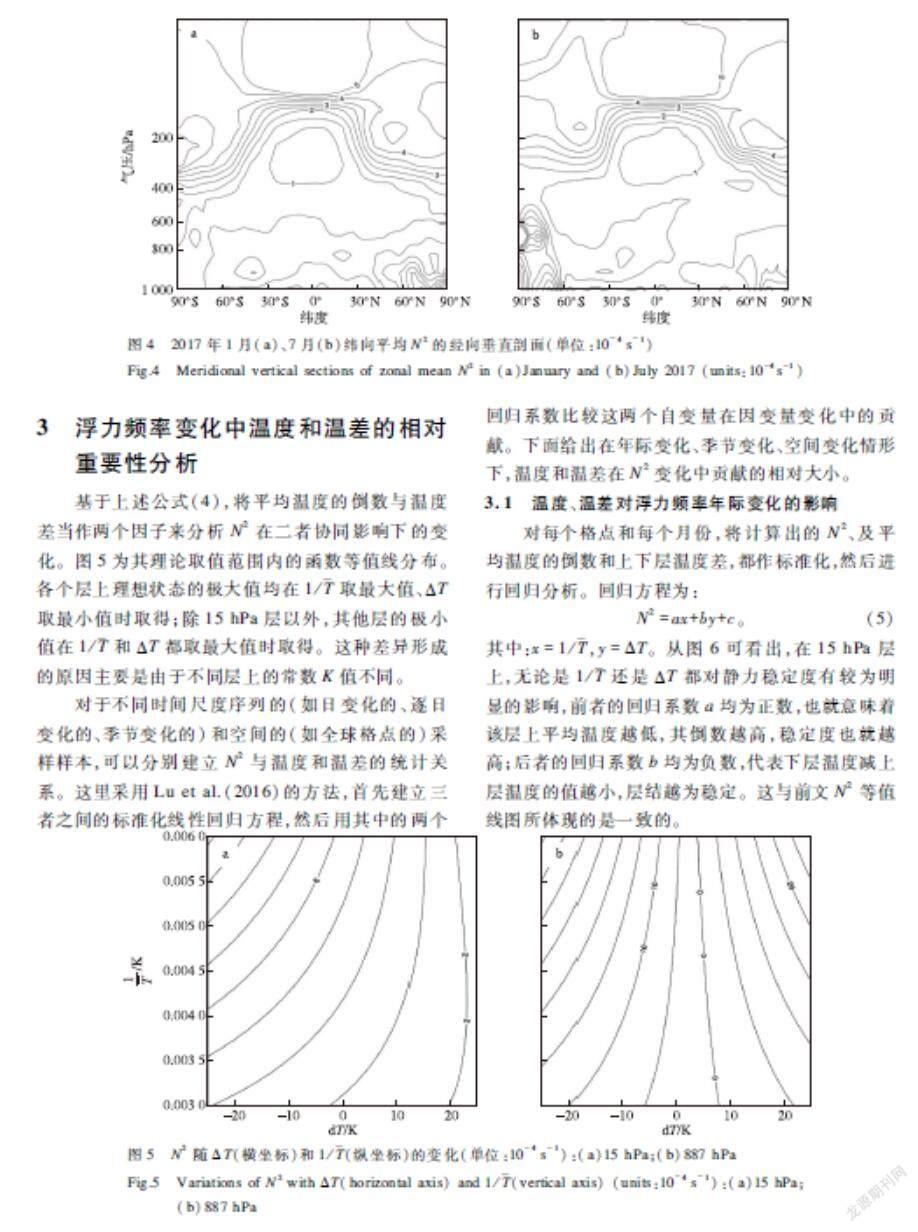
基于上述公式（4），將平均溫度的倒數與溫度差當作兩個因子來分析N2在二者協同影響下的變化。圖5為其理論取值范圍內的函數等值線分布。各個層上理想狀態的極大值均在1/取最大值、ΔT取最小值時取得;除15 hPa層以外，其他層的極小值在1/和ΔT都取最大值時取得。這種差異形成的原因主要是由于不同層上的常數K值不同。

對于不同時間尺度序列的（如日變化的、逐日變化的、季節變化的）和空間的（如全球格點的）采樣樣本，可以分別建立N2與溫度和溫差的統計關系。這里采用Lu et al.（2016）的方法，首先建立三者之間的標準化線性回歸方程，然后用其中的兩個回歸系數比較這兩個自變量在因變量變化中的貢獻。下面給出在年際變化、季節變化、空間變化情形下，溫度和溫差在N2變化中貢獻的相對大小。

3.1 溫度、溫差對浮力頻率年際變化的影響

對每個格點和每個月份，將計算出的N2、及平均溫度的倒數和上下層溫度差，都作標準化，然后進行回歸分析。回歸方程為：

N2=ax+by+c。? （5）

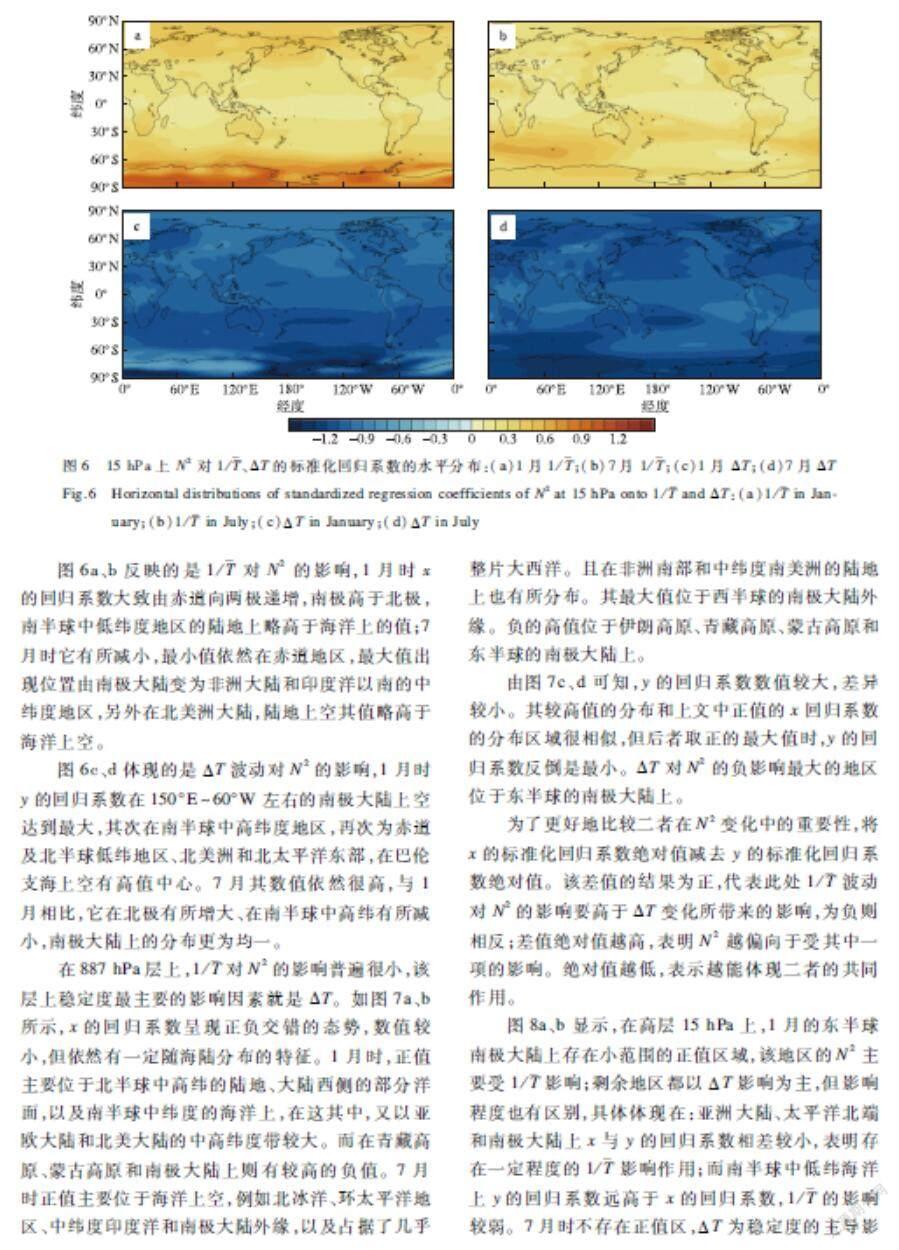
其中：x=1/，y=ΔT。從圖6可看出，在15 hPa層上，無論是1/還是ΔT都對靜力穩定度有較為明顯的影響，前者的回歸系數a均為正數，也就意味著該層上平均溫度越低，其倒數越高，穩定度也就越高;后者的回歸系數b均為負數，代表下層溫度減上層溫度的值越小，層結越為穩定。這與前文N2等值線圖所體現的是一致的。

圖6a、b反映的是1/對N2的影響，1月時x的回歸系數大致由赤道向兩極遞增，南極高于北極，南半球中低緯度地區的陸地上略高于海洋上的值;7月時它有所減小，最小值依然在赤道地區，最大值出現位置由南極大陸變為非洲大陸和印度洋以南的中緯度地區，另外在北美洲大陸，陸地上空其值略高于海洋上空。

圖6c、d體現的是ΔT波動對N2的影響，1月時y的回歸系數在150°E～60°W左右的南極大陸上空達到最大，其次在南半球中高緯度地區，再次為赤道及北半球低緯地區、北美洲和北太平洋東部，在巴倫支海上空有高值中心。7月其數值依然很高，與1月相比，它在北極有所增大、在南半球中高緯有所減小，南極大陸上的分布更為均一。

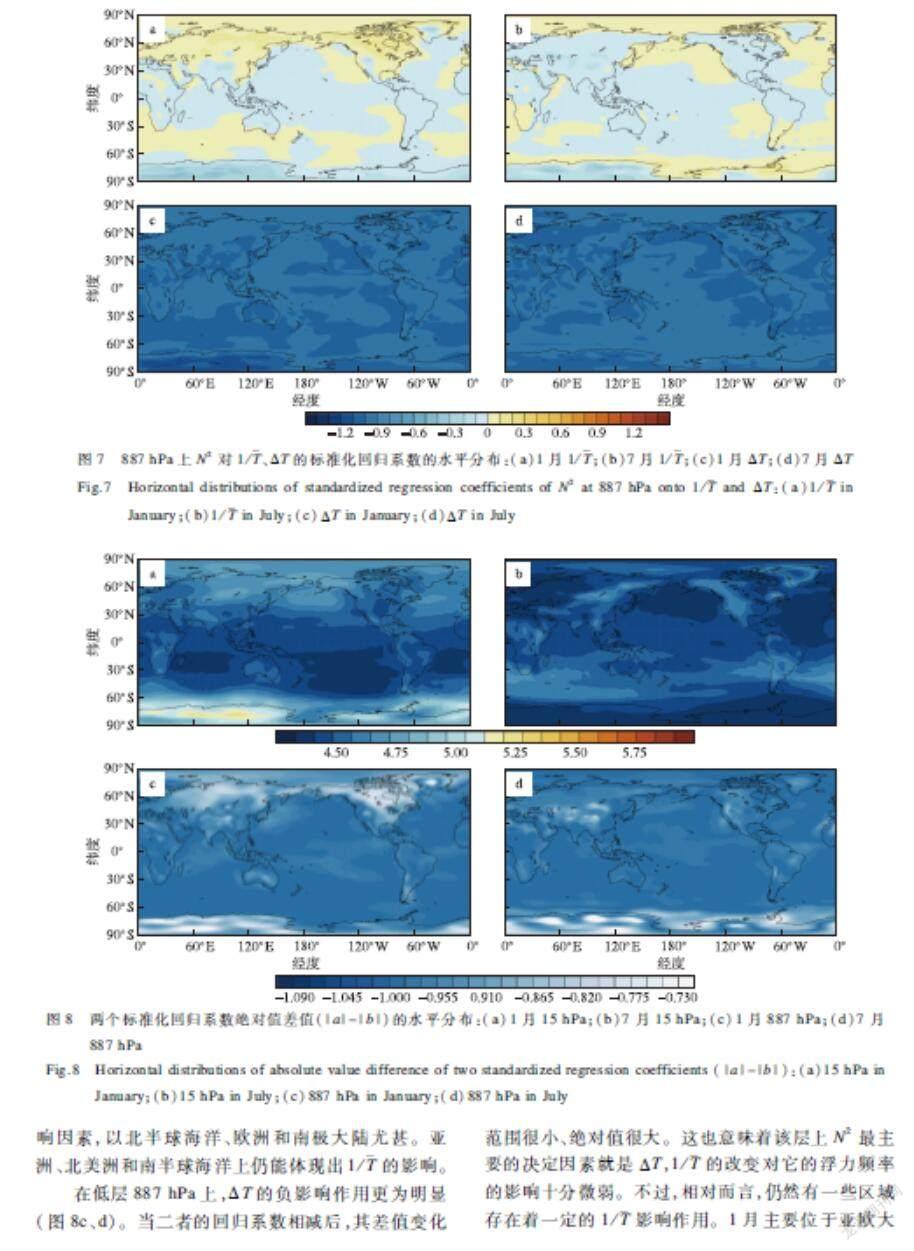
在887 hPa層上，1/對N2的影響普遍很小，該層上穩定度最主要的影響因素就是ΔT。如圖7a、b所示，x的回歸系數呈現正負交錯的態勢，數值較小，但依然有一定隨海陸分布的特征。1月時，正值主要位于北半球中高緯的陸地、大陸西側的部分洋面，以及南半球中緯度的海洋上，在這其中，又以亞歐大陸和北美大陸的中高緯度帶較大。而在青藏高原、蒙古高原和南極大陸上則有較高的負值。7月時正值主要位于海洋上空，例如北冰洋、環太平洋地區、中緯度印度洋和南極大陸外緣，以及占據了幾乎整片大西洋。且在非洲南部和中緯度南美洲的陸地上也有所分布。其最大值位于西半球的南極大陸外緣。負的高值位于伊朗高原、青藏高原、蒙古高原和東半球的南極大陸上。

由圖7c、d可知，y的回歸系數數值較大，差異較小。其較高值的分布和上文中正值的x回歸系數的分布區域很相似，但后者取正的最大值時，y的回歸系數反倒是最小。ΔT對N2的負影響最大的地區位于東半球的南極大陸上。

為了更好地比較二者在N2變化中的重要性，將x的標準化回歸系數絕對值減去y的標準化回歸系數絕對值。該差值的結果為正，代表此處1/波動對N2的影響要高于ΔT變化所帶來的影響，為負則相反;差值絕對值越高，表明N2越偏向于受其中一項的影響。絕對值越低，表示越能體現二者的共同作用。

圖8a、b顯示，在高層15 hPa上，1月的東半球南極大陸上存在小范圍的正值區域，該地區的N2主要受1/影響;剩余地區都以ΔT影響為主，但影響程度也有區別，具體體現在：亞洲大陸、太平洋北端和南極大陸上x與y的回歸系數相差較小，表明存在一定程度的1/影響作用;而南半球中低緯海洋上y的回歸系數遠高于x的回歸系數，1/的影響較弱。7月時不存在正值區，ΔT為穩定度的主導影響因素，以北半球海洋、歐洲和南極大陸尤甚。亞洲、北美洲和南半球海洋上仍能體現出1/的影響。

在低層887 hPa上，ΔT的負影響作用更為明顯（圖8c、d）。當二者的回歸系數相減后，其差值變化范圍很小、絕對值很大。這也意味著該層上N2最主要的決定因素就是ΔT，1/的改變對它的浮力頻率的影響十分微弱。不過，相對而言，仍然有一些區域存在著一定的1/影響作用。1月主要位于亞歐大陸和北美大陸的中緯度地區和南極大陸上，7月位于南極大陸沿岸。此外主要山脈和高原上空也有零星分布。

聯系圖3與圖8可看出，在高層15 hPa層上，南北半球中低緯度N2取到高值的地區（即山脈、高原上空）幾乎都表現出了1/和ΔT的共同影響，1月時南北兩極出現的低值和高值均有1/的作用，7月時兩極的高低值則主要由ΔT產生。而在低層887 hPa上，極地的高值也有少許1/的影響。

3.2 溫度、溫差對浮力頻率季節變化的影響

在回歸分析中，樣本的選取影響著回歸后的結果。在前文進行回歸計算時，用的是固定格點70 a的同1月的月平均溫度資料。剔除了季節變化和空間變化后，對一個固定點來說，它的1/的年際變化很小。而討論兩要素對某一因變量的相對影響作用時，除了回歸系數之外，要素自身的波動程度也會對其產生的重要性帶來一定的影響。因此可通過選取不同樣本，進一步理解1/、ΔT對N2的影響程度。

將所有季節都納入考量后，對指定格點共計840個月份的月平均N2與x和y進行回歸，此時計算結果所體現出的重要性則偏向于年循環的意義上溫度和溫差對穩定度的影響能力。由圖9可知，在這種情況下，15 hPa高緯度地區1/的影響有所加重，而低緯度地區則沒有明顯變化。同時，原本有明顯季節差異的y的回歸系數分布變得非常不均勻，ΔT影響最大的區域出現在北半球高緯和南半球中緯度地區，數值上有一定提升。

在887 hPa層上，絕大部分地區1/的影響依然很小，但值得注意的是在前文所提到的蒙古高原、青藏高原和南極大陸上空，以及落基山脈和格陵蘭島上，x的回歸系數有明顯升高，而在這些地點，y的回歸系數則大幅減小。進行合成后可知，從年循環角度看，在上述區域低層N2的變化中，1/的波動與ΔT的改變扮演著幾乎同等重要的角色。

3.3 溫度、溫差對浮力頻率空間差異的影響

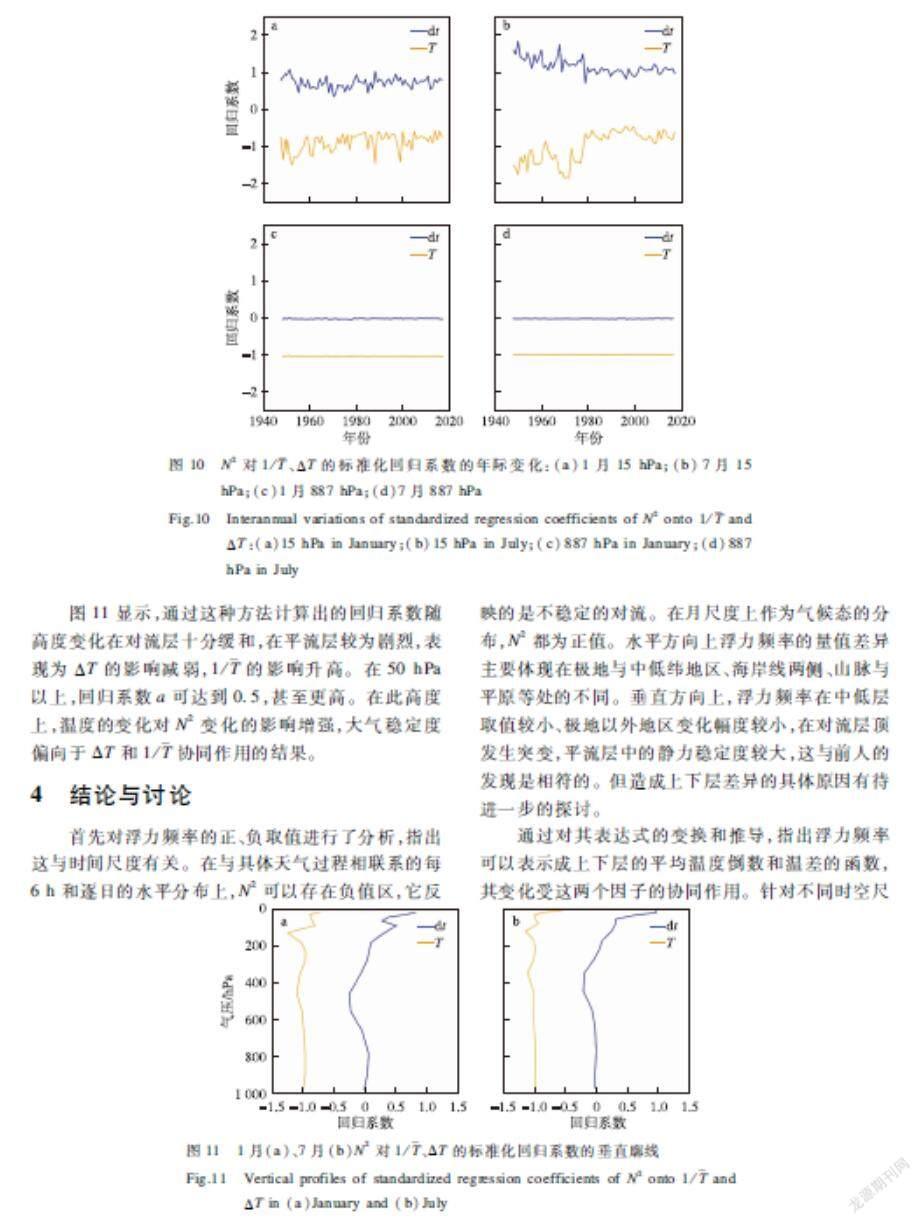
進一步研究溫度的空間分布變化。將某一等壓面上的所有格點當作樣本進行回歸，所計算出的將會是兩個因素對N2的影響程度隨時間、高度的改變。如圖10所示，高層15 hPa上，x和y的回歸系數存在準兩年的變化特征，且波動較大。陳權亮等（2005）指出平流層浮力頻率自身有著準兩年的周期振蕩，在赤道低緯度地區尤為明顯，是由于熱帶平流層緯向風的準兩年振蕩引起了溫度場的改變。而低層887 hPa上，兩個系數波動非常小，幾乎是一穩定的常數，同樣證明了前文中所指出的觀點，即低層N2最主要的影響因素是ΔT。且在70 a里，7月15 hPa層上x與y的回歸系數絕對值整體上呈現下降的趨勢，同時波動程度也有所減弱。

圖11顯示，通過這種方法計算出的回歸系數隨高度變化在對流層十分緩和，在平流層較為劇烈，表現為ΔT的影響減弱，1/的影響升高。在50 hPa以上，回歸系數a可達到0.5，甚至更高。在此高度上，溫度的變化對N2變化的影響增強，大氣穩定度偏向于ΔT和1/協同作用的結果。

4 結論與討論

首先對浮力頻率的正、負取值進行了分析，指出這與時間尺度有關。在與具體天氣過程相聯系的每6 h和逐日的水平分布上，N2可以存在負值區，它反映的是不穩定的對流。在月尺度上作為氣候態的分布，N2都為正值。水平方向上浮力頻率的量值差異主要體現在極地與中低緯地區、海岸線兩側、山脈與平原等處的不同。垂直方向上，浮力頻率在中低層取值較小、極地以外地區變化幅度較小，在對流層頂發生突變，平流層中的靜力穩定度較大，這與前人的發現是相符的。但造成上下層差異的具體原因有待進一步的探討。

通過對其表達式的變換和推導，指出浮力頻率可以表示成上下層的平均溫度倒數和溫差的函數，其變化受這兩個因子的協同作用。針對不同時空尺度的采樣樣本，對這兩個因子的相對重要性進行了分析。在浮力頻率的年際變化中，高層的部分地區可體現出二者的協同作用，其余大部分地區以及低層都由溫差主導。在年循環中，平均溫度改變的重要性有所增加，以低層的山脈和高原上的增加幅度尤為明顯。而空間變化的浮力頻率樣本則表明，溫度對浮力頻率的影響在平流層才開始有明顯增大。

需要指出的是，由于浮力頻率與重力波等環流相聯系，通過環流它也可能更進一步的與降水發生關聯。初步認為，負值的靜力穩定度N2與對流降水相關，而正值的N2也會以波動傳播的形式影響著周邊區域的降水。已有模擬研究顯示，不同大小的、正值的N2可通過改變地形重力波的方式影響大地形降水（姚昊，2009）。最近也已進行了這方面的研究，發現浮力頻率與降水之間存在一定關聯，具體影響的程度和方式將在今后的研究中進一步探討。

參考文獻（References）

Angell J K，Pack D H，Delver N，1969.Brunt-vaisala oscillations in the planetary boundary layer[J].J Atmos Sci，26（6）：1245-1252.doi：10.1175/1520-0469（1969）026<1245：bvoitp>2.0.co;2.

Brund D，1927.The period of simple vertical oscillations in the atmosphere[J].Quart J Roy Meteor Soc，53（221）：30-32.doi：10.1002/qj.49705322103.

蔡樹群，甘子鈞，仇德忠，1997.三次樣條插值在浮性頻率計算中的應用[J].熱帶海洋，16（3）：54-62. Cai S Q，Gan Z J，Qiu D Z，1997.A spline method for estimating buoyancy frequency[J].Trop Oceanol，16（3）：54-62.（in Chinese）.

陳權亮，陳月娟，鄧淑梅，2005.平流層Brunt-Vaisala頻率的分布特征[J].中國科學技術大學學報，35（6）：909-918. Chen Q L，Chen Y J，Deng S M，2005.Distribution of brunt-vaisala frequency in the stratosphere[J].J Univ Sci Technol China，35（6）：909-918.doi：10.3969/j.issn.0253-2778.2005.06.028.（in Chinese）.

Eaton B，2016.Description of the NCAR Community Atmosphere Model（CAM5.0） Boulder[R].Colorado：National Center for Atmospheric Research.

方長芳，2010.全球變暖對北太平洋年代際變化的影響及可能機制研究[D].青島：中國海洋大學. Fang C F，2010.The effect of global warming on North Pacific decadal variability and the possible mechanism[D].Qingdao：Ocean University of China.（in Chinese）.

Haren H V，2005.Internal waves near the buoyancy frequency in a narrow wave-guide[J].Journal of Sea Research，53（3）：121-129.

Kalnay E，Kanamitsu M，Kistler R，et al.，1996.The NCEP/NCAR 40-year reanalysis project[J].Bull Amer Meteor Soc，77：437-472.

李麥村，1978.重力波對特大暴雨的觸發作用[J].大氣科學，2（3）：201-209. Li M C，1978.The triggering of gravity wave to excessive heavy rains[J].Scientia Atmospherica Sinica，2（3）：201-209.（in Chinese）.

林本達，高山月，1994.定常行星波的垂直傳播及其動力學效應[J].大氣科學，18（增刊）：889-901. Lin B D，Gao S Y，1994.The vertical propagation of stationary planetary waves and its dynamic effects[J].Scientia Atmospherica Sinica，18（S）：889-901.（in Chinese）.

劉棟，高守亭，2003.飽和濕大氣Brunt-Vaisala頻率及修正的相當位溫[J].氣象學報，61（3）：379-383. Liu D，Gao S T，2003.The Brunt-Vaisala frequency in a saturated atmosphere and the revised equivalent potential temperature[J].Acta Meterologica Sinica，61（3）：379-383.（in Chinese）.

Lu E，Ding Y，Zhou B，et al.，2016.Is the interannual variability of summer rainfall in China dominated by precipitation frequency or intensity？An analysis of relative importance[J].Clim Dyn，47（1/2）：67-77.doi：10.1007/s00382-015-2822-8.

呂美仲，侯志明，周毅，2004.動力氣象學[M].北京：氣象出版社：201-202. Lü M Z，Hou Z M，Zhou Y，2004.Dynamic meteorology[M].Beijing：China Meteorological Press：201-202.（in Chinese）.

McHugh J P，2015.Incidence and reflection of internal waves and wave-induced currents at a jump in buoyancy frequency[J].Nonlin Processes Geophys，22（3）：259-274.doi：10.5194/npg-22-259-2015.

蒲書箴，于衛東，程軍，2004.熱帶西太平洋浮力頻率的垂直分布和經向變化[J].海洋科學進展，22（3）：275-283. Pu S Z，Yu W D，Cheng J，2004.Longitudinal variabilities and vertical distributions of buoyancy frequency in the western tropical Pacific Ocean[J].Adv Mar Sci，22（3）：275-283.doi：10.3969/j.issn.1671-6647.2004.03.003.（in Chinese）.

舒斯，韓芳蓉，許建玉，2015.一次暴雨過程中湖北西北部和東北部降水差異的成因分析[J].大氣科學學報，38（2）：249-258. Shu S，Han F R，Xu J Y，2015.Cause analysis of precipitation difference between northwest and northeast Hubei in a torrential rain process[J].Trans Atmos Sci，38（2）：249-258.doi：10.13878/j.cnki.dqkxxb.20140102001.（in Chinese）.

Vaisala V，1925.Uber die Wirkung der Windschwankungen auf die Pilot beobachtungen[J].Soc Sci Fennica，Commentationes Phys.-MathⅡ，2（19）：37-46.

王文，劉佳，蔡曉軍，2011.重力波對青藏高原東側一次暴雨過程的影響[J].大氣科學學報，34（6）：737-747. Wang W，Liu J，Cai X J，2011.Impact of mesoscale gravity waves on a heavy rainfall event in the east side of the Tibetan Plateau[J].Trans Atmos Sci，34（6）：737-747.doi：10.3969/j.issn.1674-7097.2011.06.012.（in Chinese）.

姚昊，潘曉濱，臧增亮，等，2009.靜力穩定度對大地形降水影響的數值模擬研究[J].氣象與減災研究，32（2）：20-26. Yao H，Pan X B，Zang Z L，et al.，2009.Numeric simulation of the impact of static stability on the precipitation induced by the high mountain[J].Meteorology and Disaster Reduction Research，32（2）：20-26.（in Chinese）.

朱莉，丁治英，張騰飛，等，2010.重力波與低緯高原地區MβCSs地域特征的關系[J].大氣科學學報，33（5）：561-568. Zhu L，Ding Z Y，Zhang T F，et al.，2010.Relationship between gravity wave and MβCSss local features on low latitude plateau[J].Trans Atmos Sci，33（5）：561-568.doi：10.3969/j.issn.1674-7097.2010.05.007.（in Chinese）.

Dominance analysis of factors influencing temporal-spatial variations of atmospheric buoyancy frequency

YANG Kexin，LU Er，ZHAO Wei

Key Laboratory of Meteorological Disaster，Ministry of Education （KLME）/Collaborative Innovation Center on Forecast and Evaluation of Meteorological Disasters （CIC-FEMD），Nanjing University of Information Science and Technology，Nanjing 210044，China

Buoyancy frequency is an important concept in atmospheric dynamics.Based on NCEP/NCAR reanalysis data，the data of four times a day，daily average and monthly average are used as inputs to calculate，and the temporal and spatial changes of buoyancy frequency at different scales are analyzed.It is found that the spatial distribution of buoyancy frequency is related to latitude and altitude，ocean and land，mountains and terrain.It is generally believed that the buoyancy frequency depends on the temperature difference between the upper and lower layers.Through the deduction of its expression，it is pointed out that the buoyancy frequency is not only related to the temperature difference between the upper and lower layers，but also related to the temperature itself，which can be expressed as a nonlinear function of the two.The relative importance of air temperature and vertical temperature difference in the temporal and spatial variations of buoyancy frequency is studied by a statistical fitting method.Results show that for some temporal and spatial variations of the buoyancy frequency，the variation of air temperature itself is also very important in some areas，and its influence can even exceed the effect of temperature difference between the upper and lower layers.

buoyancy frequency;temporal and spatial variations;air temperature;vertical temperature difference;relative importance

doi：10.13878/j.cnki.dqkxxb.20181022001

（責任編輯：張福穎）