軸對稱矢量噴管空間運動學建模仿真

柳亞冰，符大偉，蔡常鵬，孫豐勇，張海波

（1.中國航發控制系統研究所，江蘇無錫214063；2.南京航空航天大學能源與動力學院，南京210016）

0 引言

軸對稱矢量噴管由GE 公司于20 世紀80 年代中期首先研制成功并應用在F-15、F-16 推力矢量驗證機上[1-3]。而在中國，軸對稱矢量噴管應用于殲10B推力矢量驗證機并在2018 年珠海航展上亮相，系列高難度超機動飛行驗證了軸對稱矢量噴管能夠賦予戰機更為優異的機動性能。在普通噴管的基礎上，軸對稱矢量噴管通過結構上拓展擴張段的功能，使噴管在產生超聲速氣流的同時方向發生偏轉。擴張段的偏轉由各擴張調節片的空間運動組合而成，各調節片及其連桿的運動則由作動筒帶動控制環的整體偏轉來控制[4-6]。在矢量噴管實際控制試驗中，常出現噴管動態控制效果不佳，矢量軌跡不理想的情況。雖然在穩定狀態下噴管能運動到位，但是在過渡狀態下的推力矢量方向存在不確定性，給飛行穩定性帶來隱患[7]。需要設計偏轉控制規律，以實現對動態軌跡的要求。目前國內外鮮有矢量偏轉規律方面的文獻報道。

本文從軸對稱矢量噴管的運動學分析著手，建立描述噴管矢量參數與作動筒位移之間映射關系的運動學模型，并基于運動學仿真結論，設計了用于噴管動態控制的偏轉規律。

1 噴管空間運動學建模分析

軸對稱矢量噴管推力矢量方向為矢量偏轉角α和矢量方位角β，如圖1 所示。從圖中可見，令A8喉道截面中心與A9面中心的連線為噴管幾何推力矢量，則該矢量與發動機軸線的空間夾角即為矢量偏轉角α；該矢量在A8平面上的投影與發動機機匣坐標系y軸的夾角為矢量方位角β。噴管作動系統從功能角度可以分為A8調節系統和A9調節系統，如圖2 所示。A8調節系統由控制裝置、作動筒、A8調節環、凸輪副、收斂調節片、收斂段密封片等組成。多個作動筒同步輸出推動A8調節環，經過凸輪副的作用，將水平位移轉化為收斂段調節片的旋轉，從而改變A8喉道面積[8]。

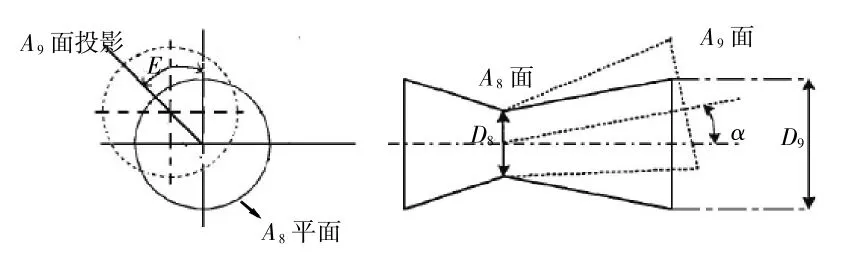
圖1 軸對稱矢量噴管推力矢量定義

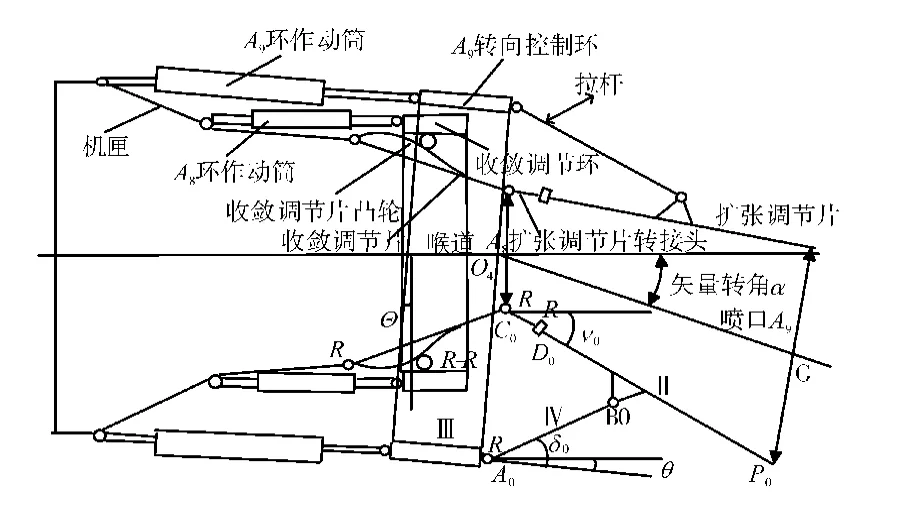
圖2 軸對稱矢量噴管結構

A9調節系統包括控制裝置、作動筒、A9環定心機構、A9轉向控制環、拉桿、擴張調節片等。當給定各作動筒的位移不同步時，A9環發生偏轉，從而帶動了A9截面面積和推力矢量方向的變化。

A9調節系統是非常復雜的空間運動結構，A9面（α、β、A9）的控制基本上是由3 個球鉸鏈-移動副-球鉸鏈（Spheric hinge-Sliding pair-Spheric hinge，SPS）作動筒協同作動實現的。A9環的3 自由度特性參數包括平臺法線矢量偏轉角θ、矢量方位角ξ、環定心側中心與機匣平面的距離l0。A9環和拉桿通過旋轉副R 副相連，旋轉角度為δi，拉桿AB通常連接在擴張調節片的中部，B點與擴張調節片之間的距離為lh。擴張調節片的末端中點為P點，A9截面可看作是由一系列離散P點組成的。擴張調節片通過十字轉接頭（2 個互為空間垂直的R 副）連接在A8截面上，分別通過D、C點處的2 個R 副實現擴張調節片在徑向平面和周向平面內的偏轉，角度分別為vi和ωi。每個連桿-調節片單元如圖3 所示[9]。

圖3 A9調節系統單元

從圖3 中可見，在A9系統作動筒起始端所在的機匣平面上分別定義2 個坐標系：機匣坐標系Oxy0z0和基準坐標系Oxy1z1。機匣坐標系為定坐標系，基準坐標系上矢量方位角始終為0。通過建立這2 個坐標系，采用運動的分解原理[10]，將A9調節系統的空間運動分解為：

（1）控制環先繞Oz3坐標軸（機匣坐標系Oz0坐標軸沿x軸平移到環定心點O3處）旋轉θ，該運動下控制環的法向量始終位于Oxy0平面內，運動結果為A9環法線矢量偏轉角為θ，A9面矢量偏轉角為α，而方位角仍為0。

（2）再將控制環及桿系繞x軸旋轉ξ，使環法線矢量偏離Oxy0平面而落到Oxy1平面內，則A9環及A9面的矢量方位角變為β或ξ。

由A9面求解A9環的研究在基準坐標系下進行；由A9環求解作動筒位移的研究在機匣坐標系下進行。基于上述分析，本文在王玉新[11]的研究基礎上進一步簡化了推導過程，提高了模型平衡方程的準確性。

從空間運動學的角度來看，A9調節系統需要在保證結構完整穩定的基礎上使面積和偏轉矢量角滿足指令需求，因此存在3 個約束：結構穩定性Bi（拉桿定長）約束、矢量角度α約束、面積A9約束，可分別描述為

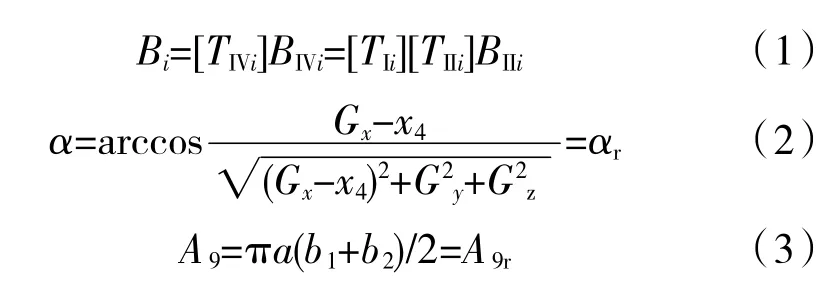
式中：TIVi為環上任意一點Ai處的連桿坐標系變換矩陣；BIVi= [lAB001]T為Bi在連桿坐標系下的相對坐標；TIi為CiDi構件坐標系還原為基準坐標系的變換矩陣；TIIi為擴張調節片CiPi構件坐標系相對CiDi坐標系的變換矩陣；BIIi= [lBC，0，-lh]T為BIIi在擴張調節片坐標系下的相對坐標；Gx、Gy、Gz分別為噴管出口截面幾何中心沿坐標軸x、y、z的坐標；a、b1、b2分別為出口截面2 個半橢圓的軸長，即P1G、P0G、P2G。通過坐標系轉換可以獲取上述變換矩陣

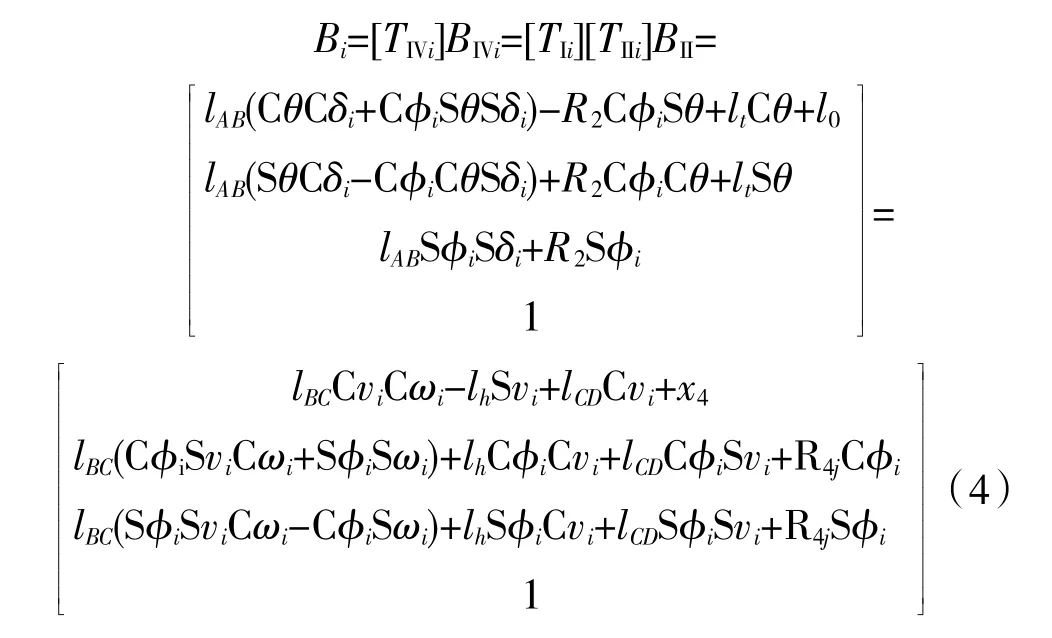
式中：C 為cos 的縮寫；Φi為第i個位置點方位角；S為sin 的縮寫；R2為A9轉向控制環半徑；R4為擴張調節片轉接頭喉道截面半徑。

A9出口截面可以看作由2 個半橢圓拼成，如圖4所示。選擇4 個特殊端點，包括2 個非對稱位置P0、P2和2 個對稱位置P1、P3。定義偏轉矢量與發動機軸線構成的平面為偏轉平面，該平面A9截面的交點即為P0、P2，分別對應于圖2 中截面下、上兩側的擴張調節片的末端。2 個對稱位置P1、P3分別為偏轉平面兩側中間調節片的末端；矢量角度α約束公式（2）中的G點為出口截面A9的幾何中心，即為P1、P3的中心，且在偏轉平面上。

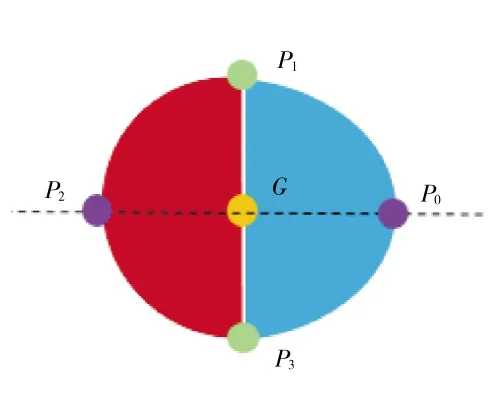
圖4 A9出口截面

結構穩定性約束公式（1）中的Bi點分別選在這4個特殊位置處。在P0處，φ0=0，ω=0，代入式（4）中得到在B0處的平衡方程f1、f2為

在P2處，Φ0=π，ω=0，代入式（4）中得到B2處的平衡方程f3、f4為

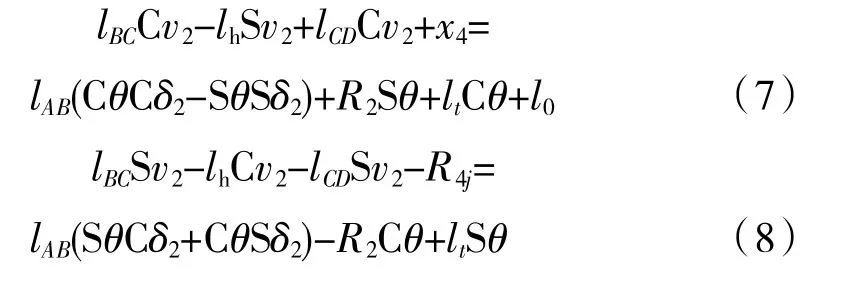
在P1處，Φ0=π/2，代入式（4）中得到B1處的平衡方程f5、f6、f7為

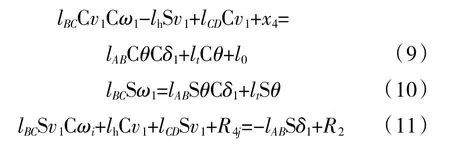
幾個特殊位置Pi點的基準坐標通過將相對坐標PIIi=[lCP，0，0]T代入式（12）求解

進而代入式（2）、（3），構成平衡方程f8、f9。

綜上所述，f1～f99 個平衡方程描述了A9調節系統需要滿足的定長約束、面積約束以及角度約束等，構成了軸對稱矢量噴管的運動學模型

未知參數為x=[v0，δ0，v2，δ2，v1，ω1，δ1，θ，l0]T，輸入參數為y=[α，A9，A8]T。可以采用Newton-Raphson 算法求解。其中，根據運動的分解中由A9面求解A9環的研究在基準坐標系下進行，故β未考量。在求解出A9控制環的l0和θ后，再結合ξ=β，在機匣坐標系下根據作動環的位姿[l0，θ，ξ]T可對3 個作動筒的位移進行求解[12]

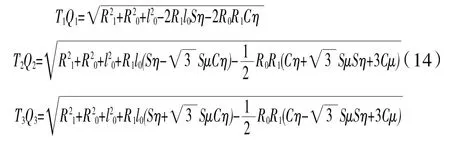
2 噴管空間運動學模型仿真

首先以噴管未偏轉狀態作為設計點進行幾何尺寸參數整理和確定，喉道面積取為0.302 m2，A9/A8=1.25。

主要尺寸參數設計結果見表1，此時各組件空間運動參數見表2。

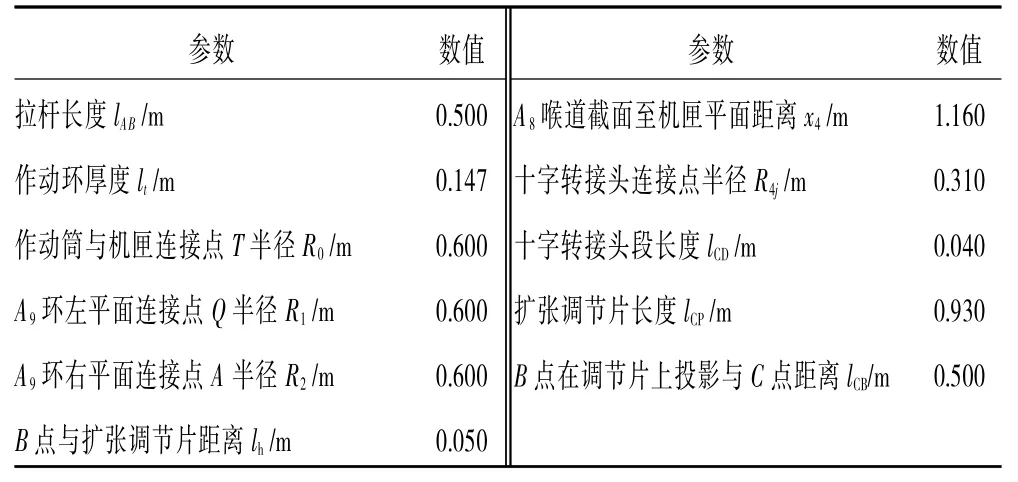
表1 幾何尺寸參數設計結果

表2 設計點下參數求解結果

設計點的計算表明，當推力矢量不發生偏轉時，各調節片和拉桿的空間狀態相同，A9出口截面為圓形。

矢量偏角α從0 增大到20°，模型解算各參數變化如圖5 所示。

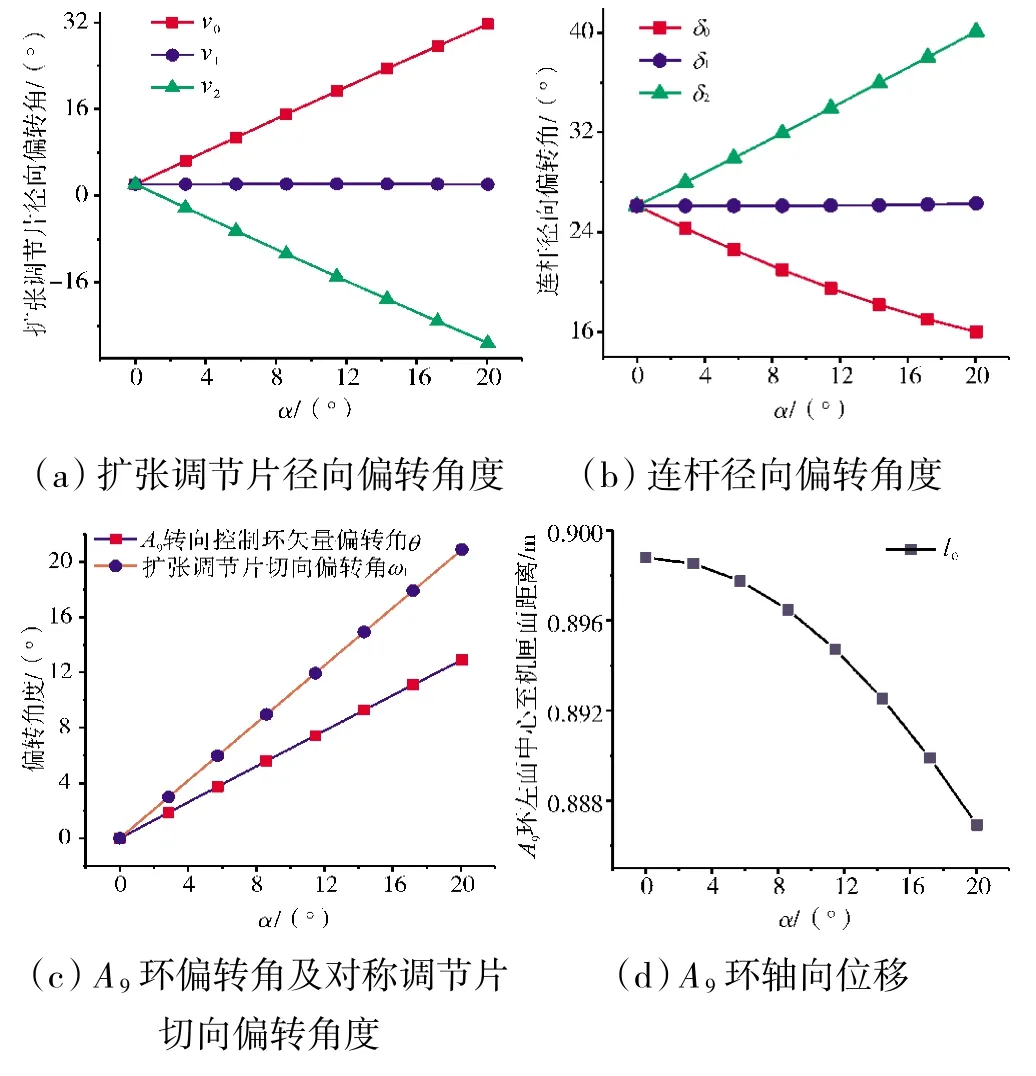
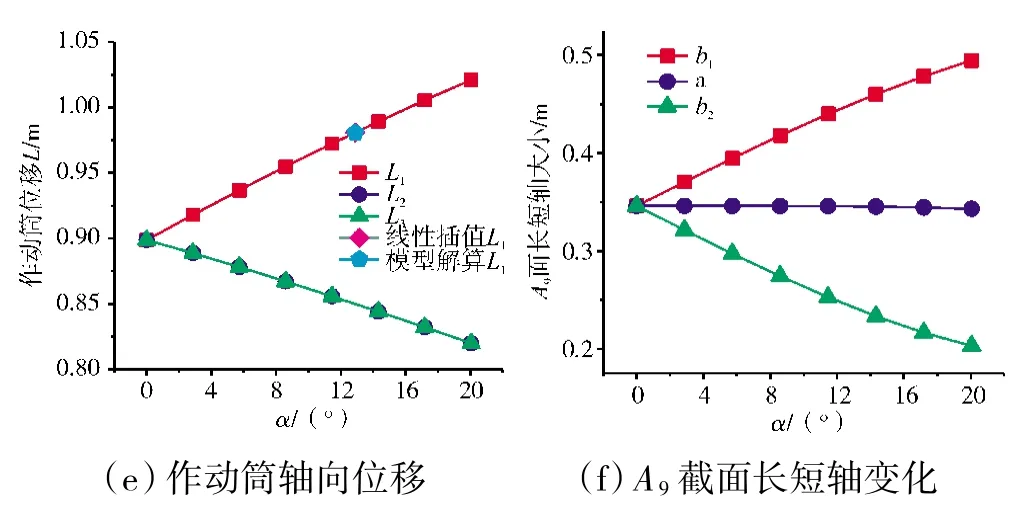
圖5 不同偏轉角下的運動學參數變化

隨著α增大，矢量方向對應的0 位置的擴張調節片偏轉角度逐漸增大，連桿偏轉角度減小；對應的反向2 位置處的調節片偏轉角度減小，連桿偏轉角度增大，從而帶動A9面中心向最遠位置一側偏移。兩側1和3 位置處的調節片和連桿的徑向偏轉角度則基本不變，而調節片切向旋轉角ω1與α之間基本呈ω1=α的變化關系，說明本文設計的噴管作動系統的A9面矢量偏轉角主要由對稱位置擴張調節片的切向偏轉決定。隨著α增大，y軸正方向上的作動筒L1的位移量增大，與之夾角均為120°而對稱分列兩邊作動筒L2和L3位移量相同且減小，幅度比L1的略小。作動筒變α曲線基本呈線性，1 維線性插值結果與模型解算結果基本一致，根據該曲線即可由輸入參數α插值出3 個作動筒的位移指令并進行控制。A9截面以對稱位置為界分為2 個半橢圓，由于對稱位置擴張調節片的徑向偏轉角v1在不同α下基本不變，因此為定值；受相關約束的影響，兩非對稱位置調節片末端與幾何中心的距離均隨α發生改變，但根據式（3）中的面積約束，b1+b2保持為定值。

令矢量偏轉角α恒定為17.2°，矢量方位角β從0°逐漸增大到360°，此時A9轉向控制環的矢量偏轉角θ、l0保持恒定，而方位角ξ隨β變化。因此除了特殊位置所對應的實際擴張調節片-連桿系在不斷變化外，其他所有參數均保持不變。此外，由于作動筒的空間位置均固定，因此需要每個作動筒的位移相應地改變，根據式（14）得到矢量方位角變化對3 個作動筒位移指令要求的影響規律如圖6 所示。

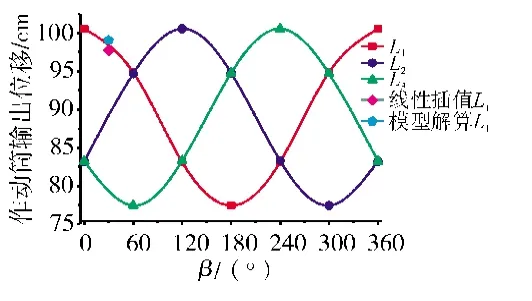
圖6 不同方位角下作動筒位移變化

將α和β的影響規律相結合，基于空間運動學模型計算建立2 維插值模型，如圖7 所示。該2 維插值模型可以看作是上述1 維等偏轉角和等方位角曲線分別在偏轉角和方位角維度上的延伸。當α=0 時，3個作動筒的等α線均為1 條定值直線。隨著α增大，等α線開始呈現出與圖6 相似的變化趨勢，且幅值逐漸增大；等β線則描述了與圖5 相似的變化趨勢，且每條等β線都是單調的。

上述2 維插值模型描述了在A8、A9幾何面積固定的前提下，矢量偏轉角及矢量方位角與3 個作動筒之間的輸入輸出關系。在空間運動學模型迭代求解時間較長，占用內存量大，通過插值模型可以較快地根據矢量角指令插取軸對稱矢量噴管開環控制下3 個作動筒的輸入指令。完整的插值模型維度為4，即在2 維模型的基礎上，加上A8和A92 個維度[13]。

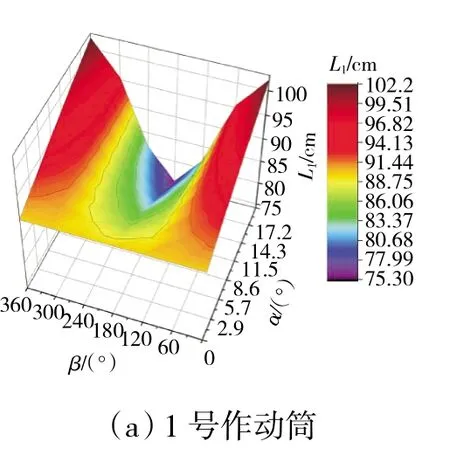
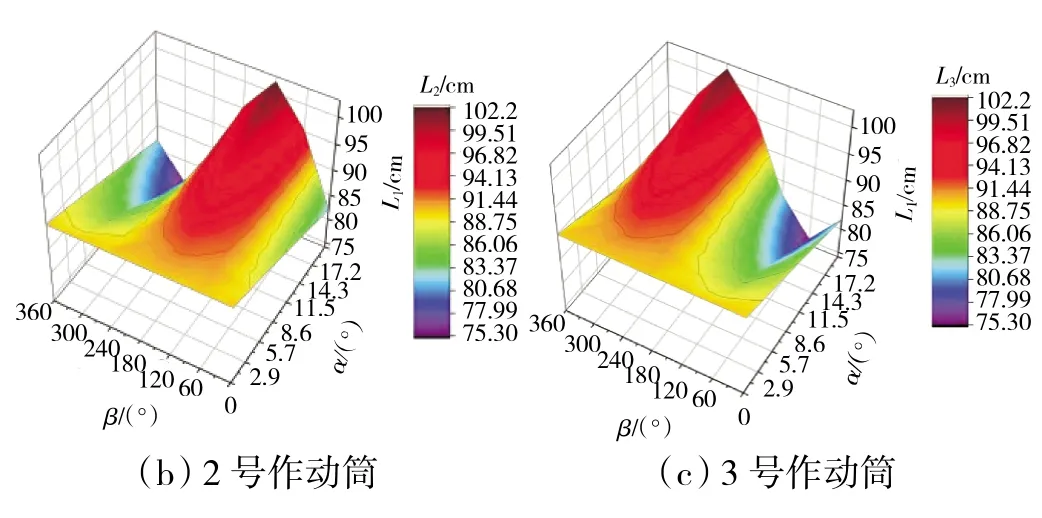
圖7 2 維插值模型

3 噴管偏轉規律初探

由于噴管的矢量角度、面積等參數不能直接被傳感器測得，因此軸對稱矢量噴管采用開環控制；對單個作動筒可通過位移傳感器獲取反饋量，采用閉環控制。控制的動態性能和穩態性能受偏轉指令反解作動筒位移控制指令的插值模型精度、偏轉規律、單作動筒小閉環控制器、作動筒協同控制規律共同影響[14]，如圖8 所示。噴管矢量偏轉通常要在規定時間內完成，由初始狀態[α1，β1]T轉變為目標狀態[α2，β2]T，若無合適的偏轉規律，位移插值由終了狀態直接輸入作動筒的位移指令可以看作是階躍信號。令矢量噴管的控制周期與發動機控制周期相同，均為20 ms，通過偏轉規律計算每個控制周期下的偏轉指令，階躍信號轉化為類斜坡信號，再通過誤差綜合耦合器和控制算法在每個控制周期內對當前指令信號進行跟蹤，從而實現噴管矢量偏轉的動態可控性。

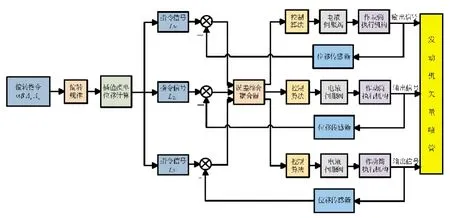
圖8 軸對稱矢量噴管A9調節系統控制

噴管矢量α和β的動態變化情況可轉化為A9面幾何中心G點空間運動的軌跡。第2 章的研究表明，當A8、A9面積固定，G點空間坐標的秩為2 且α、β的改變對Gx的影響較小可忽略時，α、β的變化轉化為Gy、Gz的變化，即簡化為G點空間運動軌跡在Oyz平面內的投影。為了使噴管的矢量狀態切換直接快速，偏轉規律的設計約束之一為該投影是1 條直線，如圖9 所示。

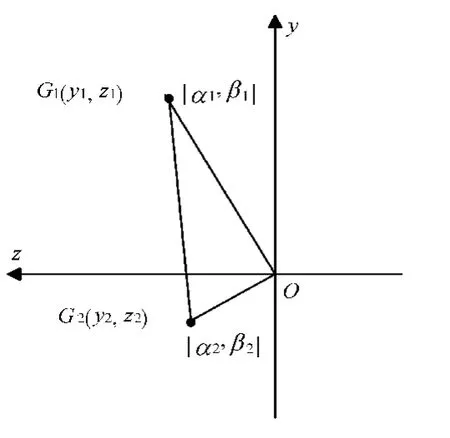
圖9 設計規律下的噴管矢量投影面軌跡

從圖中可見，O點為發動機軸線Ox的投影。由于偏轉中矢量長度lGO4基本不變，因此[α，β]T與坐標之間的轉換可簡化為

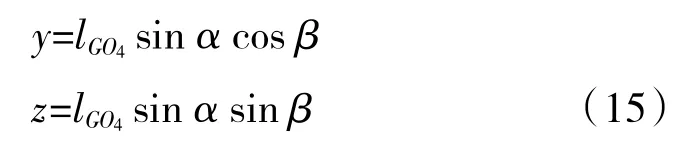
當噴管穩定在初始狀態1 時，作動筒液壓力與噴管內壁氣動負載力相平衡；當給出偏轉指令后，作動筒滑油流量逐漸改變，液壓力逐漸改變，受力失衡，作動筒開始產生位移；觀察G點軌跡，運動加速度和速度大小均從0 開始緩緩增加。為了避免作動筒活塞突然停止帶來的控制困難和構件沖擊，當噴管運動逼近狀態2 時，運動加速度和速度大小均緩緩降為0。因此，從G1到G2的過程中，幾何中心移動速度先增大再減小，加速度先為正再為負，變化曲線設計為正弦函數[15]

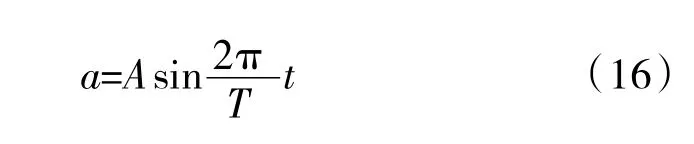
式中：T為矢量偏轉時長；A為待求系數。

積分并代入(t，v)邊界條件：（0，0）和（T，0），得速度曲線為余弦曲線

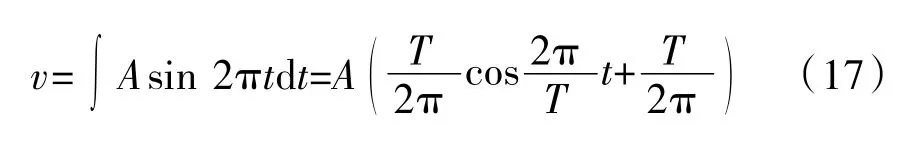
繼續積分并代入(t，s)邊界條件：（0，0）和（T，ls），解得系數A及位移曲線

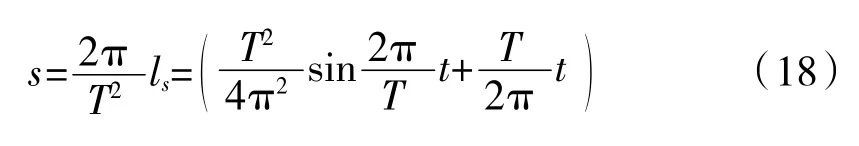
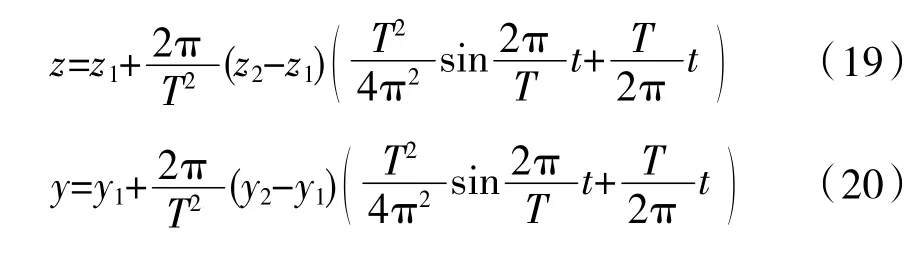
再結合式（15），將中心坐標變化規律轉化為噴管矢量角度α、β的偏轉規律

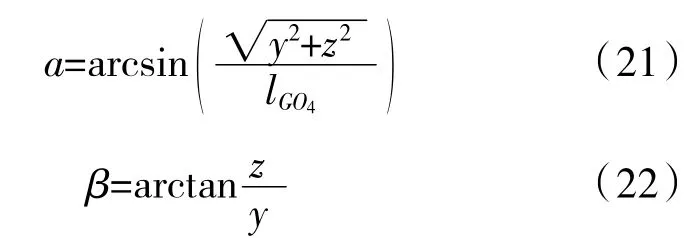
令噴管初始狀態[α1，β1]T為[11.46，π/6]T，目標狀態[α2， β2]T=[5.73， 2π/3]T，偏轉時間定為1 s。上述偏轉規律的仿真結果如圖10所示。

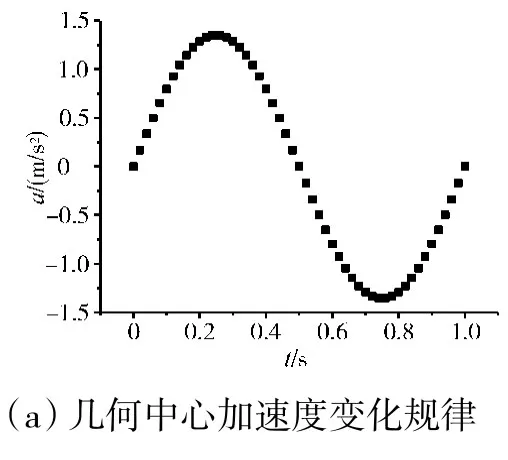
圖10 噴管偏轉規律仿真結果

仿真結果表明，由于起步和結束時的緩沖作用，幾何中心軌跡曲線分別呈現加、減速的效果。矢量方位角變化規律為一單調的曲線，佐證了矢量狀態切換的直接性；偏轉角變化規律則不是單調的，α最小值出現在0.65 s 左右，這是因為O點到G1G2連線上任意點的最短距離出現在垂足位置。

根據每個控制周期內的α、β角度指令，代入空間運動學穩態數學模型或位移插值模型，解算得到3 個作動筒的位移指令，變化規律如圖11 所示。進一步令穩態數學模型代替實際噴管開展數字仿真驗證，檢驗在該調節規律下各控制周期內A9幾何中心的軌跡。

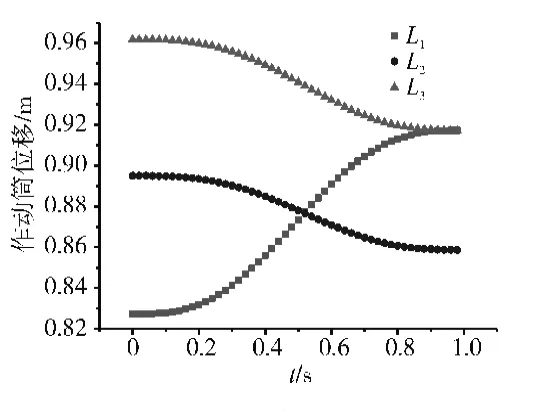
圖11 作動筒調節規律

在作動筒調節規律中，作動筒之間位移差距隨時間呈減小趨勢，原因在于偏轉角α隨時間減小而使作動筒位移幅值減小，滿足2 維仿真規律；各作動筒隨時間的增減趨勢也與變β仿真中方位角β減小時的規律相一致。該位移調節規律與實際作動筒的運動特性曲線相接近，容易控制實現，具有較好的工程應用價值。

設計調節規律下幾何中心軌跡驗證結果如圖12所示，從圖中可見，在該調節規律下幾何中心軌跡的投影與終末連線的偏差微乎其微，從而驗證了該調節規律設計理論推導的正確性。但是在實際中，每個控制周期下幾何中心的位置還與作動筒控制器、作動筒間協同控制算法的控制效果有關，也是本文圍繞軸對稱矢量噴管的后續研究方向之一[16-17]。

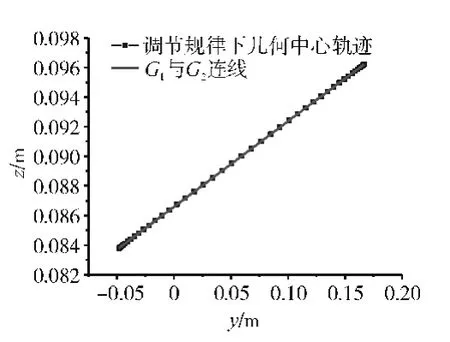
圖12 設計調節規律下幾何中心軌跡驗證

4 結論

本文針對噴管矢量軌跡動態可控的技術需求，在軸對稱矢量噴管模型方面做了相關研究，得出以下結論：

（1）通過空間運動學分析揭示了軸對稱矢量噴管系統中作動筒位移與噴管出口矢量之間的映射關系，建模仿真結果表明矢量偏轉角主要由對稱位置擴張調節片的切向旋轉角決定，矢量方位角的影響體現在作動筒位移的周期性變化上。

（2）針對矢量噴管動態控制的研究需求，本文在傳統的協同控制方案的基礎上提出設計偏轉規律的解決方案，結合作動筒的實際運動規律將加速度和速度規律設計為三角函數。仿真結果表明該調節規律可較好地使噴管矢量的動態軌跡滿足設計要求。