與積分有關(guān)的一個(gè)極限及其應(yīng)用

黃永忠， 吳 潔

(華中科技大學(xué) >數(shù)學(xué)與統(tǒng)計(jì)學(xué)院，武漢430074)

1 引 言

與定積分有關(guān)的極限問(wèn)題常常涉及綜合知識(shí)，有一定難度但同時(shí)也有一些好的結(jié)論，見(jiàn)文[1-8]. 文[9]綜合習(xí)題第62題：

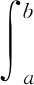
這個(gè)結(jié)論的證明較容易，基本思路是用“擬合法”(見(jiàn)命題1的證明). 文[9]的接下來(lái)63題就是這個(gè)結(jié)果的應(yīng)用題(見(jiàn)例4)，其實(shí)第6題也是這個(gè)結(jié)論的應(yīng)用題(見(jiàn)例1).

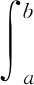
2 對(duì)應(yīng)數(shù)列極限及其應(yīng)用

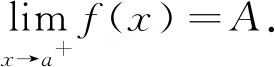
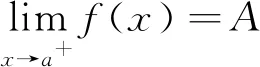
|f(x)-A|<ε.

注意到

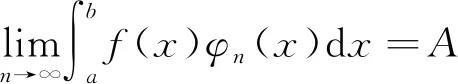
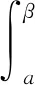
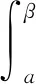
隨后幾個(gè)命題可作相應(yīng)說(shuō)明，不再提及.

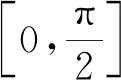
證利用Beta函數(shù)和Gamma函數(shù)，得

(1)

其中等價(jià)關(guān)系由下列Stirling公式而得

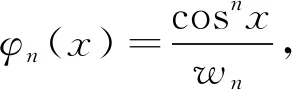
注2 利用本例，特別是式(1)， 可立即簡(jiǎn)潔地得到文[10]第1.46題的極限(其中f，g是連續(xù)函數(shù)).

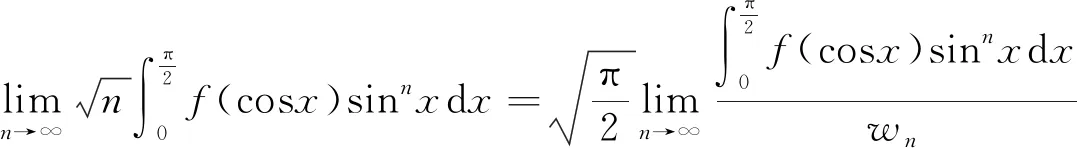
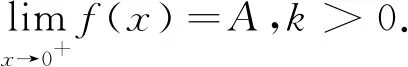
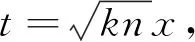
因?yàn)?/p>

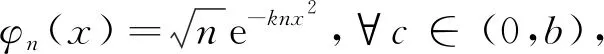
即φn(x)在[c，b]上一致收斂于零， 所以由命題1后注1得

下例來(lái)自文[10]， 那里用Lebesgue控制收斂定理，這里用命題1.

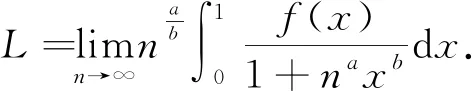
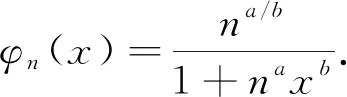
?c∈(0，1)，φn(x)在[c，1]上滿足

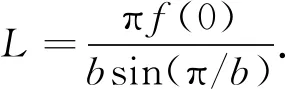
對(duì)偶地，有如下結(jié)論：

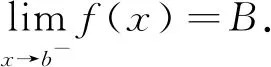
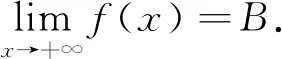
例4[9]設(shè)函數(shù)f(x)在積分區(qū)間上連續(xù)，求下列極限：

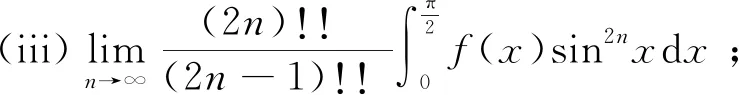
解因?yàn)閤n在右端點(diǎn)1的任何區(qū)間上不一致收斂，所以(1)與f(1)有關(guān). 余下題可類似把握.

(i) 設(shè)φn(x)=(n+1)xn，則它滿足命題1′對(duì)φn(x)的條件，從而得到

(ii) 令t=x2，利用Beta函數(shù)得

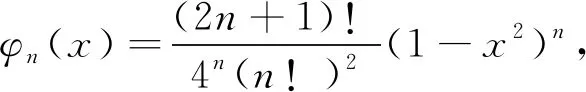
也就是φn(x)在[0，c]上一致收斂于零. 因此，由命題1，有

下面例5來(lái)自文[10]第1.45題，做法與文[10]不同， 那里用到有界收斂定理，這在通常的數(shù)學(xué)分析或微積分教材中并不提及.

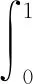
解設(shè)m，M為正常數(shù)，且m≤f(x)≤M(x∈[0，1])，則

從而由迫斂性定理得到

所求極限為1∞型. 于是利用等價(jià)關(guān)系ln(1+y)～y(y→0)知，求極限J歸結(jié)為求極限

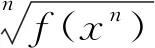
|lnf(xn)|≤C，x∈[0，1].

由不等式

得到

于是

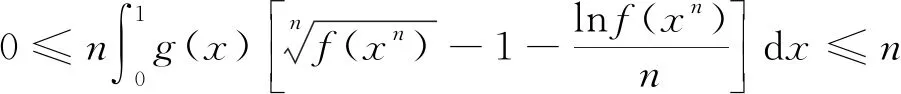
因此，令t=xn，有

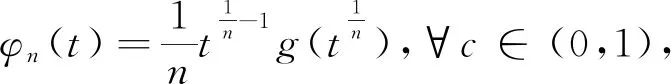
也就是φn(t)在[c，1]上一致收斂于零，其中常數(shù)β使0≤g(x)≤β(x∈[0，1]). 因此由命題1得L=lnf(0)，從而得所求極限J=f(0).

3 對(duì)應(yīng)函數(shù)極限及其應(yīng)用

定義設(shè)Uo(x0，δ′)為實(shí)數(shù)x0的一個(gè)去心鄰域，I?R是一個(gè)區(qū)間. 對(duì)定義在平面區(qū)域Uo(x0，δ′)×I上的函數(shù)w(x，y)，稱w(x，y)當(dāng)x→x0時(shí)關(guān)于y在I上一致收斂于零，是指?ε>0，存在δ>0(δ≤δ′)，當(dāng)0<|x-x0|<δ時(shí)，?y∈I有|w(x，y)|<ε.

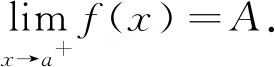
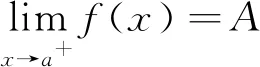
|f(x)-A|<ε.

注意到

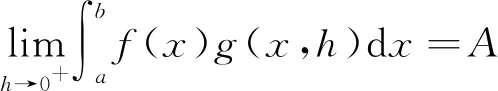
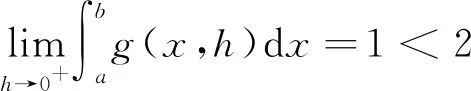
這里沒(méi)有用函數(shù)的上極限. 命題1的證明后段也可以如這里的處理，用極限的定義.

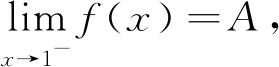
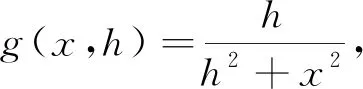
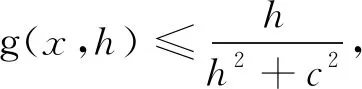
為方便應(yīng)用，下面給出命題3和命題4，其證明與命題2雷同，從略.

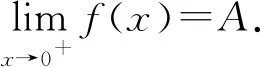
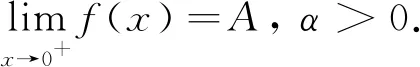
解令μ(x，t)=xαt-(1+α)，則

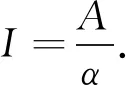
注4 若f(x)在[0，1]上連續(xù)，則本題可用洛必達(dá)法則來(lái)做.

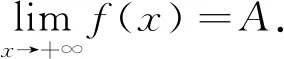
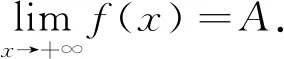
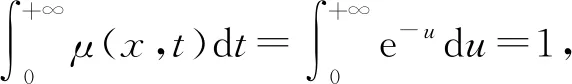
4 結(jié) 論

本文對(duì)文[9]的一道綜合習(xí)題進(jìn)行推廣，得到相應(yīng)數(shù)列極限和函數(shù)極限的計(jì)算式子，其中的積分可以是變限的也可以是瑕積分、無(wú)窮積分等，并通過(guò)較多的例子展現(xiàn)了這種推廣的全面性和有效性.

致謝作者非常感謝相關(guān)文獻(xiàn)對(duì)本文的啟發(fā)以及審稿專家提出的寶貴意見(jiàn).