詣零換位子中心環的一些刻畫

邵雨凡， 陳建華， 魏俊潮

(揚州大學 >數學科學學院，江蘇 >揚州225002)

1 引 言

環的交換性的眾多條件，優美且有對稱性，但經過時代的發展，環論學者發現研究的環的交換性條件過于復雜，或是失去了創新性.隨著探究的深入，在近十年來，環論學者將重點轉移到局部化的半交換性問題上，如文獻[1-3]中所研究的CN環、JTTC環和擬正規環等，探究這些環的性質并利用這些環刻畫一些經典的環類，更寬泛地詮釋了半交換性問題所具有的意義與價值.本文基于對冪零元素及冪等元素的探究，主要研究在局部交換性條件下環所呈現的性質，給出詣零換位子中心環的若干性質和刻畫，其價值在于研究的結合環的半交換性問題保持了環的交換性的若干性質，但條件的放寬意味著適合更多的環類，同時應用性也得到增強.

本文中，R表示有單位元的結合環、N(R)表示R的全體冪零元的集合、Z(R)表示R的中心、E(R)表示R的全體冪等元集合.

定義1[4-6]若對任意a∈N(R)，x∈R，總有[a，x]∈Z(R)，其中環上兩個元素a與x的交換子定義為[a，x]=ax-xa，則稱R為詣零換位子中心環，簡稱NC環.若E(R)?Z(R)，則稱R為Abel環.若N(R)={0}，則稱R為約化環.若對任意a∈R，當aRa={0}，總有a=0，則稱R為半素環.設I是R的理想，若I中的每個元素都是R的冪零元素，則稱I是R的詣零理想；若N(R)∩I={0}，則稱I為R的約化理想.若對任意x，y∈R，總有[x，y]∈Z(R)，則稱R為換位子交換環.

顯然交換環總是換位子交換環，但由文獻[7]知，換位子交換環未必為交換環，除非R為半素環.換位子交換環當然是NC環.

定義2[8]設a∈R，若存在b∈R，使得a=aba，則稱a是R的正則元；若存在b，c∈R，使得a=a2b=ca2，則稱a是R的強正則元.

定義3[9-10]設a∈R，若存在b∈R，使得a=aba，b=bab，ab=ba，則稱a為R的群可逆元，且稱b為a的群逆元，通常記為a#.用R#表示R的全體群可逆元的集合.

定義4[11]設*∶R→R為雙射，滿足條件：

(a*)*=a， (a+b)*=a*+b*， (ab)*=b*a*，

則稱R為卷積環或*-環.設R為*-環，a∈R，若存在c∈R，使得

a=aca，c=cac， (ac)*=ac， (ca)*=ca，

則稱a為Moore Penrose可逆元，簡稱MP可逆元，且稱c為a的MP逆元，記為a+.用R+表示R的全體MP可逆元的集合.設a∈R#∩R+，若a#=a+，則稱a為R的EP元.用REP表示R的全體EP元的集合.

2 主要結果

NC環是一類特殊的結合環，下面通過研究NC環與多種環之間的聯系，給出NC環的性質和刻畫.命題1指出NC環實際上也是Abel環.

命題1NC環為Abel環.

證設R為NC環.任取e∈E(R)，任取a∈R，記h1=(1-e)ae，h2=ea(1-e)，則

h1e=h1，eh1=0=h2e，h2=eh2，

而

注意到

[h1，e]=h1e-eh1=h1-0=h1， [h2，e]=h2e-eh2=0-h2=-h2，

所以h1，h2∈Z(R)，從而

h1=h1e=eh1=0，h2=eh2=h2e=0.

因此對每個a∈R，ae=eae=ea，從而e∈Z(R)，故R為Abel環.

注1 命題1的逆命題不成立：

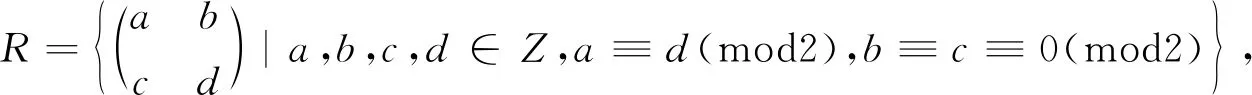
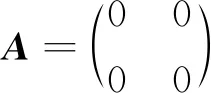
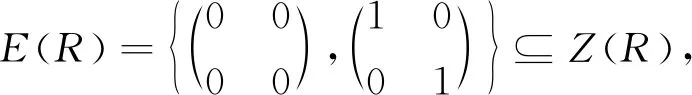
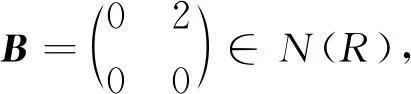
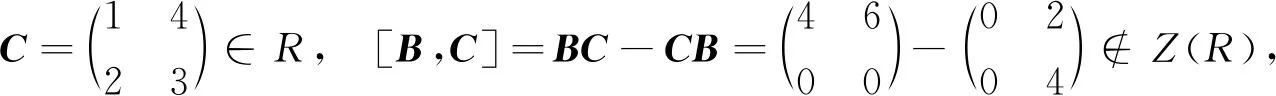
故R不為NC環.

設

則根據通常的矩陣加法及乘法，WT3(R)成為一個環. 借助于NC環，下面的命題給出了交換環的一個刻畫.

命題2R為交換環當且僅當WT3(R)是NC環.

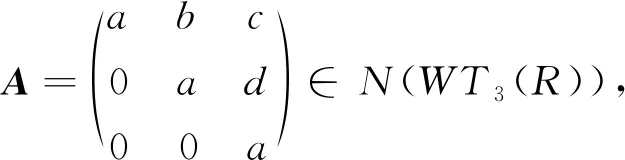
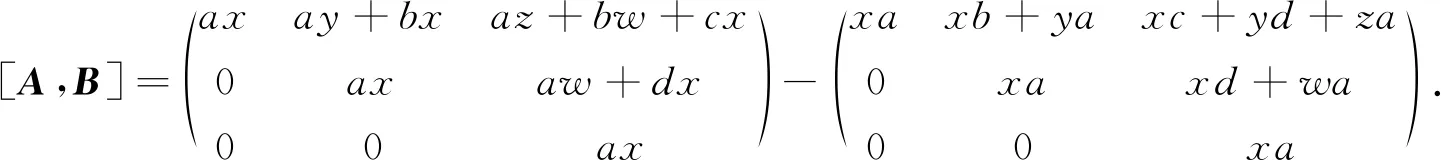
由于R為交換環，故

于是WT3(R)是NC環.

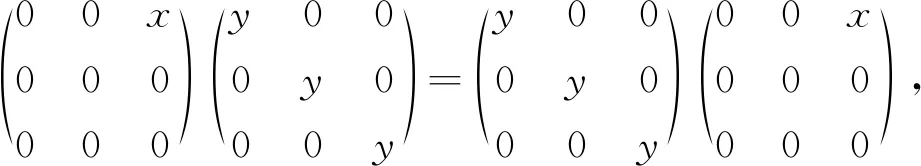
即

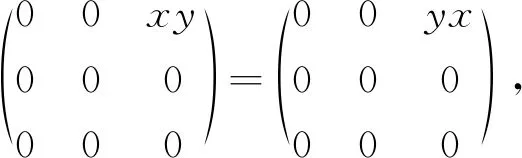
所以xy=yx，于是R為交換環.

設

則根據通常的矩陣加法及乘法，V2(R)成為一個環.

命題3設R為交換環，則V2(R)為NC環.

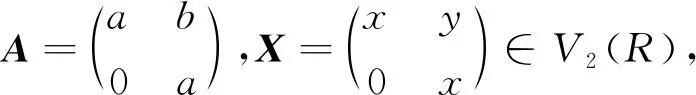
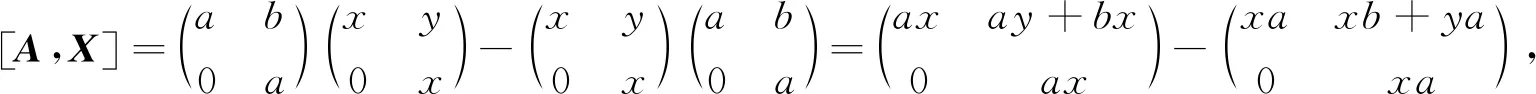
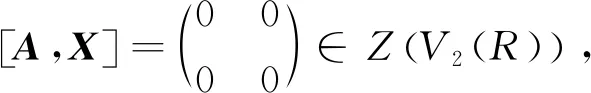
注2 命題3的逆命題不成立，即當V2(R)為NC環時，R不必為交換環：設F是一個域，當取

為NC環時，R不是交換環.

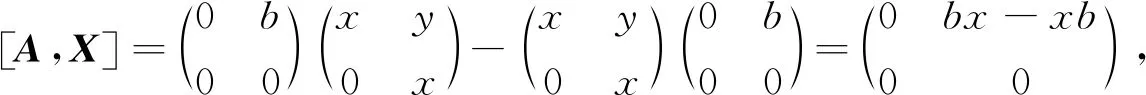
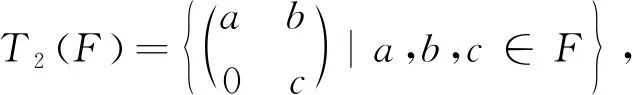
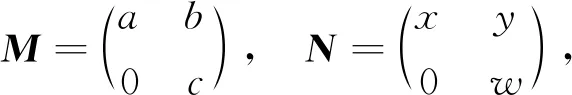
MN≠NM，所以R不是交換環.

下面利用環同構建立NC環、半素環以及交換環之間的聯系.

命題4設R為半素環，若V2(R)為NC環，則R為交換環.

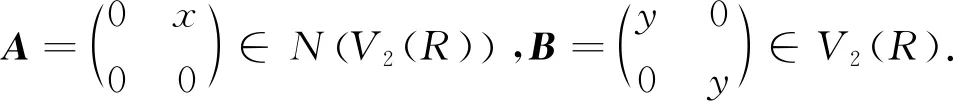
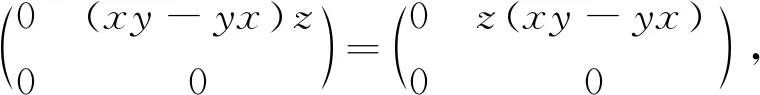
從而對任意的z∈R，(xy-yx)z=z(xy-yx)成立，因此xy-yx∈Z(R).由文獻[7]中定理1知R為交換環.

設R為半素環，記T(R，R)={(a，b)|a，b∈R}，在T(R，R)中定義加法及乘法如下：

(a，b)+(x，y)=(a+x，b+y); (a，b)(x，y)=(ax，ay+bx)，

則T(R，R)為一個環.

推論1設R為半素環，若T(R，R)為NC環，則R為交換環.

·

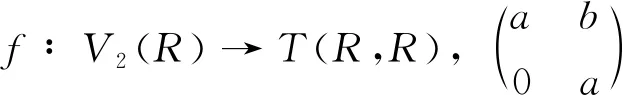
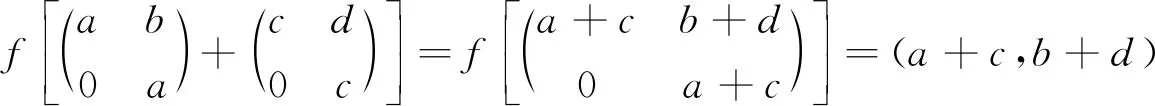
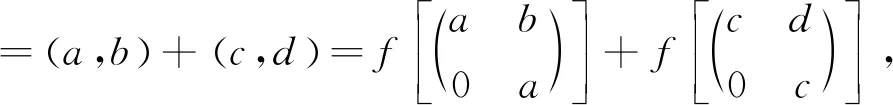
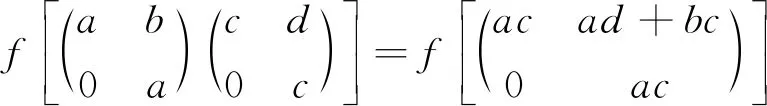
所以f是同態映射.因為對任意的a，b，c，d∈R，a=c與b=d不同時成立.

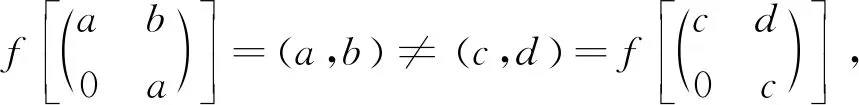
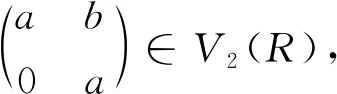
設x是一個未定元，記R[x]為R上的一元多項式環，記(x)表示由x生成的理想，則有商環R[x]/(x2)，記為R〈x〉.容易看出R〈x〉={a+bx|a，b∈R，x2=0}，定義R〈x〉中加法及乘法如下：

(a+bx)+(c+dx)=(a+c)+(b+d)x； (a+bx)(c+dx)=ac+(bc+ad)x，

則R〈x〉為一個環.

推論2設R為半素環，若R〈x〉為NC環，則R為交換環.

證構造映射g∶T(R，R)→R〈x〉，(a，b)a+bx，則容易證明g為環同構，故由推論1知R為交換環.

利用冪零元的性質以及約化理想的結構，可以得到NC環與約化環之間的聯系.

命題5設R為半素環，若V2(R)為NC環，則R為約化環.

證若N(R)≠{0}，則有0≠a∈N(R)，從而存在正整數n，使得an-1≠0而an=0，易見n≥2. 由命題4知R為交換環，故

an-1Ran-1=Ran-1an-1=Ranan-2={0}.

由于R為半素環，則an-1=0，矛盾.故N(R)={0}，所以R為約化環.

命題6設I是R的詣零理想.若R為NC環，則商環R/I也為NC環.

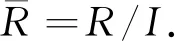
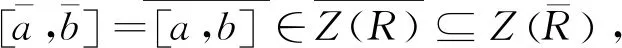
因此商環R/I也是NC環.

命題7設I為R的約化理想，若R/I為NC環，則R為NC環.

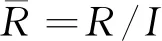
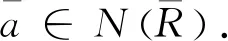
(an-1ta)2=an-1tanta=0.

由于t∈I，則an-1ta∈I，故

an-1ta∈N(R)∩I={0}.

于是an-1ta=0.因為(an-1t)2=an-1taan-2t=0，且an-1t∈I，所以an-1t=0.若n=2，則at=0；若n>2，則(an-2ta)2=0，且an-2ta∈I，故又有an-2ta=0，進一步用上述方法可證，an-2t=0.若n=3，則at=0；若n>3，則重復上述過程，至多有限步，總可得at=0.從而，對任意y∈R，有aty=0.由于(ta)2=tata=0，且ta∈I，故ta∈N(R)∩I={0}，即ta= 0，因此(ayt)2=aytayt=0.由于ayt∈I，則對任意y∈R，ayt=0.由于

t2=[(ab-ba)x-x(ab-ba)]t=a(bx)t-baxt-xabt+xbat=0，

因此t=0，從而對任意x∈R，(ab-ba)x=x(ab-ba).故[a，b]∈Z(R)，所以R為NC環.

命題8設R為有單位元的結合環，則下列條件等價：

(i)R為換位子交換環；

(ii)V2(R)是換位子交換環；

(iii)V2(R)是NC環.

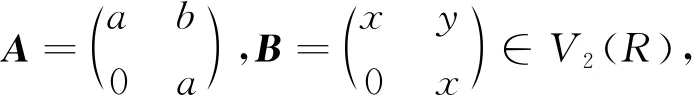
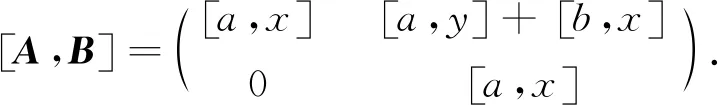
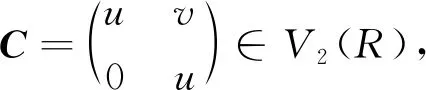
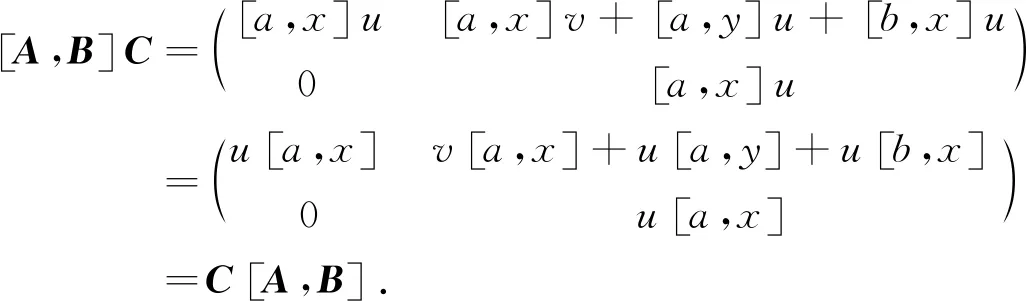
因此[A，B]∈Z(V2(R))，即V2(R)是換位子交換環.

(ii)?(iii) 顯然.

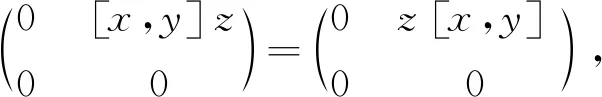
從而[x，y]z=z[x，y]，所以[x，y]∈Z(R).因此R為換位子交換環.

命題9設a是R的正則元，若R為NC環，則a是R的強正則元.

證由于a是R的正則元， 所以存在b∈R， 使得a=aba.記e=ab，g=ba，則

ea=a=ag，e2=e，g2=g.

由于R為NC環，則由命題1知R為Abel環，所以e，g∈Z(R)，于是

a2b=ae=ea=a=ag=ga=ga=ba2，

因此a是R的強正則元.

命題10設R為NC環，若a∈R+，則a∈REP.

證由于a∈R+，所以a=aa+a.由于R為NC環，由命題9的證明知a2a+=a=a+a2，從而

aa+=(a+a2)a+=a+(a2a+)=a+a.

由于a=aa+a，a+=a+aa+，所以a∈R#且a#=a+，從而a∈REP.

命題11設a∈R#∩R+，若[a#，a+]∈Z(R)，則a∈REP.

證由于[a#，a+]∈Z(R)，故[a#，a+]a=a[a#，a+]，即a#a+a-a+a#a=aa#a+-aa+a#.上式左乘a得

aa#a+a-aa+a#a=a2a#a+-a2a+a#

①

由于

aa#a+a=a#aa+a=a#a，aa+a#a=aa+aa#=aa#=a#a，a2a#a+=a(aa#)a+=a(a#a)a+=aa+，

從而①式變為aa+-a2a+a#=0，即aa+=a2a+a#.由于

a2a+a#=a2a+(a#aa#)=a2a+(aa#a#)=a(aa+a)a#a#=aaa#a#=aa#aa#=aa#，

所以aa+=aa#，故a∈REP.

3 結 論

本文主要研究了詣零換位子中心環的一些性質，刻畫了這類環的結構.分析了有單位元的結合環R與其上二階或三階矩陣環之間的關系，由此得到二階或三階矩陣環為詣零換位子中心環的條件.給出了其在局部交換性下呈現的性質，以及其與約化環、Abel環等一些重要環類的聯系.除此之外，本文還介紹了詣零換位子中心環上的正則元、強正則元的定義與一些性質，并討論了其上的廣義逆問題，為詣零換位子中心環的應用提供理論基礎.

致謝作者非常感謝相關文獻對本文的啟發以及審稿專家提出的寶貴意見.