星載天線展開過程立體視覺動態測量技術

高 越 孫增玉 袁 媛 崔忠亮

(北京航天計量測試技術研究所，北京 100076)

1 引 言

星載天線是衛星結構的重要組成部分，是直接執行衛星功能的重要平臺，受運載火箭儀器艙容納尺寸的限制，搭載衛星多采用可展開的結構形式，其中可展開天線是大口徑衛星天線結構形式的首選[1]。桁架式網狀天線收納比大、質量輕、型面精度高，綜合性能表現最為出色，適合于大口徑天線，是目前研究最多的一種星載可展開天線。桁架天線的運動部件多達幾千個，在快速展開過程中，其中任何一個部件發生問題，都將會導致天線展開失敗，使得衛星不能正常工作，致使發射任務功虧一簣[2]。因此，星載天線展開機構在地面進行的零重力模擬展開可靠性評估試驗至關重要。

可展開天線為一不穩定的體系，在展開過程中其運動速度、加速度、軌跡、約束反力等都在不斷地變化，為保證設計的可靠性需要對其展開過程做詳細分析[3]。設計者最關心的是展開過程中的幾何協調性、天線能否展開到位、在特定驅動力作用下結構展開的運動學特征，并且星載天線反射面的型面精度與天線的電性能息息相關，展開后的幾何型面參數也是關注的重點。然而，在地面模擬零重力展開試驗中，直徑約4米的星載天線在2秒以內可完全展開，展開速度大，目前借助高速攝像機錄制其展開過程視頻，通過觀察定性分析設計結構的展開可靠性。本文提出基于立體視覺測量原理的星載天線動態展開測量方法，可獲得各運動部件關鍵點的運動軌跡、速度、加速度以及展開面型等數據，為設計者進行動力學和可靠性分析提供依據。

2 立體視覺動態測量技術

基于雙目立體視覺原理，采用兩臺高速相機在同步脈沖控制器的觸發下同步采集某時刻天線的展開狀態圖像，經圖像預處理獲得該時刻空間特征點在像面上的圖像坐標，通過雙相機內外參數和視差交會模型解算出該時刻特征點的空間三維坐標。在連續等時間間隔的同步脈沖控制下，可以獲得特征點在空間的運動軌跡，經過時間微分等數據處理方法得到特征點的運動速度、加速度等運動特性參數。在完全展開處于靜態后，各特征點的三維空間坐標構成了整個天線的三維面型，可用于面型誤差的計算，系統組成如圖1所示。

圖1 動態測量系統框圖Fig.1 Block diagram of dynamic measurement system

2.1 雙目立體視覺交會坐標解算

雙目立體視覺是基于視差原理，由多幅圖像獲取物體三維幾何信息的方法[4]。已知兩個相機之間的位置關系，便可以獲取公共視場內空間物體特征點的三維坐標。如圖2所示，設Oc1-Xc1Yc1Zc1為相機L坐標系，像平面坐標系為O1-X1Y1，有效焦距為f1；Oc2-Xc2Yc2Zc2為相機2坐標系，像平面坐標系為O2-X2Y2，有效焦距為f2，將相機L坐標系作為測量系統坐標系Os-XsYsZs。

圖2 雙目視覺測量原理圖Fig.2 Binocular vision measurement principle

(1)

根據相機透視投影模型及雙相機位置關系，空間點P的三維坐標可表示為

(2)

式中：f1、f2——分別為相機L和相機R的有效焦距。

由公式(2)可知，已知有效焦距f1、f2和被測點在兩相機像平面上的精確圖像坐標(X1,Y1)、(X2,Y2)，只要求出旋轉矩陣R和平移矩陣T，即可求解獲得空間點P在測量系統坐標系下的三維坐標(xs,ys,zs)[5]。有效焦距、光心位置、鏡頭畸變等內部參數可在實驗室經基于立體靶標的標定方法獲得，而外部參數是根據雙相機在現場的架設情況確定，通過下述基于標準長度的標定方法獲得。

2.2 基于標準長度的相機外參現場標定方法

雙目立體視覺測量系統的外部參數標定主要是確定雙相機之間的相對位置關系，即視覺系統結構參數R和T[6]。由于可展開天線的口徑很大(數米甚至十幾米)，這要求雙相機公共測量視場要覆蓋整個空間，同時為保證測量精度，雙相機的基線距離也會達到數米甚至十幾米，這對雙相機系統的外參標定提出了更高的要求，經典的平面靶標尺寸無法滿足標定需求，需要設計滿足大范圍測量的現場快速標定方法。

利用測量視場中兩點之間的長度作為約束條件，實現基于標準長度的相機外參現場標定方法。用含有8個點的編碼靶標與帶有標準長度的標準桿組成新的標定結構如圖3所示，通過圖像中編碼標識的識別準確定位標尺在圖像中的位置，利用兩編碼標識中心點的標準長度作為約束，利用L-M迭代法將標準桿上的標準長度與像面上的像點坐標聯系，組成新的約束條件方程，通過迭代計算該約束條件方程，獲得高精度的標定相機外參數。

圖3 編碼靶標基準尺Fig.3 Coded target scale

設空間點P在左右相機的圖像坐標為(X1，Y1，1)和(X2，Y2，1)，根據公式(2)計算空間點P的三維坐標(xs,ys,zs)，由公式(2)中的第三式可得

f(x)=(f2t1-X2t3)(Y2(r7X1+r8Y1+f1r9)-

f2(r4X1+r5Y1+f1r6)-

(f2t2-Y2t3)(X2(r7X1+r8Y1+f1r9)-

f2(r1X1+r2Y1+f1r3)=0

(3)

其中，x=(r1,r2,r3,r4,r5,r6,r7,r8,r9,t1,t2,t3)為12個未知變量，r1～r9構成的旋轉矩陣R是正交的，具有六個正交約束條件，(t1，t2，t3)為沿X、Y、Z方向上的平移量，由此構成如下罰函數為

(4)

由所有光測點得到無約束最優目標函數為

(5)

為提高算法精度，引入基準尺的標準長度D，如圖3所示。在已經精確校準內部參數的相機像面上，通過識別編碼標識找到中心點坐標Pij(xij,yij,zij)，得到兩點的距離Di(i=1，2，3，…，n)為測量次數，(j=1，2)為每次測量的中心點位。由中心點距D引入加強約束目標函數

(6)

目標函數為

(7)

最后，由Levenberg-Marquardt法進行非線性最優化解算，獲得雙相機的外部參數。

2.3 動態多目標點識別跟蹤方法

在大型可展開天線地面展開試驗過程，大型可展開天線從收攏狀態運動到展開狀態，須同時動態拍攝并測量展開區域內的多個運動目標(200個以上)的接觸與分離狀態，各點的運動速度快且運動幅度大，相對位置關系排列準則隨時間推移將發生變化，傳統的極線約束無法滿足各點序號前后一致性的判斷，為保證各被測點序號之間不能混淆和錯亂，準確獲得各點的連續運動軌跡，須對各點進行跟蹤測量。

根據視差連續性，除了遮擋區域視差的變化應該都是平滑的，以此作為匹配約束，實現對各點的連續跟蹤。針對某一目標點為例，遍歷所有時刻進行目標點跟蹤的過程如圖4所示。首先獲取0時刻目標點中心圖像坐標(X0，Y0)，下一時刻以該點為中心的子窗口中搜索臨近點，判斷臨近點個數是否唯一，如果唯一作為該時刻目標點獲取該點中心坐標(X1，Y1)；如果不唯一則進行灰度值相關相似度約束，去除虛假點的干擾獲取滿足條件點中心坐標(X1，Y1)，然后對下一時刻進行目標提取。由于運動連續性，根據(i-1)和(i-2)時刻該點的運動方向，預判時刻i在圖像上的區域，在該區域識別目標點并獲得中心坐標。循環上述步驟，順序遍歷所有時刻實現對該點的跟蹤識別。目標點識別跟蹤流程圖如圖4所示。

圖4 動態目標點識別跟蹤過程Fig.4 Tracking process for dynamic targets

3 運動位移測量不確定度評定

3.1 運動位移測量示值誤差測試

為驗證該方法的動態測量性能，根據《JJF(軍工)70-2014運動姿態視覺測量系統校準規范》中運動位移測量誤差的校準方法，使用位移標準裝置完成位移測量示值誤差測試，如圖5所示。在位移標準裝置的移動平臺上固定一個定向反光球，運動位移標準裝置帶動反光球按給定加速度做加速運動，使最快速度可達5m/s。在加速過程中位移標準裝置分別在0mm、1000mm、3000mm、5000mm四個位置處輸出外觸發信號，觸發立體視覺動態測量系統進行同步測量，分別記錄位移標準裝置的輸出值和立體視覺動態測量系統的測量值。完成一次測量后，位移標準裝置回到0mm位置，重復測量6次。將位移標準裝置的輸出值作為運動位移參考值，取6次立體視覺動態測量系統測量值的平均值作為運動位移測量值。運動位移測量誤差為運動位移測量值減去運動位移參考值之差，取誤差中最大值作為立體視覺動態測量系統的運動位移測量示值誤差[7]。運動位移測量示值誤差測試結果如表1所示，根據表中結果按上述方法計算可得立體視覺動態測量系統的運動位移測量示值誤差為1.609mm。

圖5 動態測量系統校準方法Fig.5 Calibration method for dynamic measurement system

3.2 測量模型

測量過程中，立體視覺測量系統和位移標準裝置分別測量并記錄運動位移值和運動位移標準值建立測量模型

ΔL′=L′-L′s

(8)

式中：ΔL′——位移測量誤差；L′——位移測量值；L′s——位移標準值。

3.3 不確定度來源

標準不確定度分量來源和說明如表2所示。

表2 標準不確定度分量來源和說明Tab.2 Sourceandexplanationofstandarduncertaintycomponents序號不確定度分量符號及名稱符號不確定度分量名稱評定方法1u1測量重復性A類評定2u2外觸發同步信號延遲誤差B類評定3u3位移標準裝置讀數B類評定4u4位移標準裝置偏離標準溫度B類評定5u5位移傳感器與位移標準裝置熱膨脹系數差B類評定

3.4 標準不確定度分量評定

3.4.1測量重復性引入的標準不確定度分量u1

采用標準不確定度A類評定方法評定。在系統加速度為5m/s2條件下，經過1s后速度能夠達到5m/s，此時對應的位移值為2.5m，因此以2500mm位置為例開展不確定度分析，對該校準點位進行10次重復測量，測量結果如表3所示。

表3 重復測量結果Tab.3 Repeatedmeasurementresultmm校準點測量值25002501.2152500.6122500.8182500.4582498.7982499.6982501.0252501.2122501.1982501.374

得到實驗標準偏差s為0.817mm，此項不確定度分量為

u1=s=0.817mm

(9)

3.4.2外觸發同步信號延遲引入的不確定度分量u2

單次觸發測量延時誤差Δt在100μs以內，速度v按5000mm/s計，由此引入的標準不確定度分量按B類評定方法計算

u2=v×Δt

(10)

u2=5000×0.1×10-3=0.500mm

3.4.3運動位移標準裝置引入的不確定度分量u3

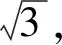
(11)

3.4.4 運動位移標準裝置偏離標準溫度引入的不確定度分量u4

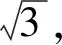
(12)

3.4.5 運動位移標準裝置與位移傳感器材料熱膨脹系數差引入的不確定度分量u5

當校準溫度偏離標準溫度時，位移標準裝置與位移傳感器由于材料熱膨脹系數不同也會引入不確定分量，由于所選用的位移傳感器與位移標準裝置材料相同，且采用貼附安裝方式，可以認為兩者熱膨脹系數相同，因此，此項誤差可忽略。

3.4.6合成標準不確定度的計算uc

各標準不確定度分量之間彼此相互獨立，合成標準不確定度為

(13)

3.4.7擴展不確定度U

取包含因子k=2，則擴展不確定度為

U=kuc=2×0.96=1.92mm

(14)

對原始數據依據格拉布斯準則剔除異常值后，以各校準點多個測量結果的平均值作該校準點的測量值，以各校準點測量誤差的最大值作為運動姿態視覺測量系統的位移測量誤差。測量系統運動位移的最大測量不確定度為1.92mm，可知該方法能夠獲得較高精度的點位、速度、加速度等運動參數，用以滿足天線展開動態運動可靠性分析的測量需求。

4 現場試驗驗證

某型桁架式單側展開網狀天線，僅需1.6s便可從收攏狀態展開到至展開狀態。針對該型天線地面模擬展開試驗，采用上述設計方案對網面上層關鍵關節點(21個)的展開運動過程進行了測量。測量系統以300fps(幀/S)的速度進行雙相機同步動態采樣，測量時間為5s，除去起始的等待時間，有效運動為1.5s，共400幅圖像，每幅圖像采樣點個數為21個。通過三維重構獲得了各點的三維空間運動軌跡、速度、加速度以及面型數據，其中各點的運動軌跡圖如圖6所示，某點的速度曲線如圖7所示。

圖6 測量點運動軌跡圖Fig.6 Trajectory of measuring points

圖7 單點運動速度曲線Fig.7 Speed curve of single point

5 結束語

本文針對星載天線地面展開試驗，運用雙目視覺測量原理開展了天線展開動態測量技術的研究。采用基于標準長度的相機外參現場標定方法，有效解決了大視場范圍的視覺外參標定問題。利用動態多目標點識別跟蹤方法，能保證觀測點序號前后一致性，準確獲得各點的連續運動軌跡。通過實驗室校準方法驗證了測量系統的運動位移測量精度，現場試驗驗證了各關鍵技術，獲得了多點目標的運動軌跡、速度、加速度以及面型數據，測量結果與運動仿真理論結果吻合，該技術可應用于天線展開過程的動態測量，為天線展開動力學分析和可靠性分析提供數據參考。