煤礦巷道錨網支護機理及圍巖變形規律分析

高議民

(山西魯能河曲電煤開發有限公司 上榆泉煤礦，山西 忻州 034000)

隨著煤礦井下開采斷面和開采深度逐漸增加，巷道所處的地質力學環境越來越復雜，受到開采擾動應力場和深部地應力場的影響，巷道開挖后處于塑性變形階段。目前常規的支護不能夠滿足巷道正常應用需求。在現場實踐中錨網支護已經被廣泛應用，但是煤礦地質條件隨著煤層、礦井、區域的不同出現很大不同，各個礦井的錨網支護機理也不盡相同。錨網支護作為現在大多數礦井使用的主要支護技術，僅依賴于錨桿的密度、剛度和強度，沒有充分考慮兩者的耦合關系，不能夠充分發揮錨網支護的潛力，錨網支護密度過大，造成資源的浪費，很多情況下，錨桿的強度已經過剩，但是其配合的護網強度卻遠遠不足，致使錨網耦合強度降低，造成巷道變形和冒頂的發生[1-3]。鑒于此，本文研究了煤礦巷道錨網支護技術及圍巖變形規律，實現了井下快速施工，提高了煤礦的經濟和社會效益。

1 工程概況

研究礦井生產規模為90萬t/a，井田南北寬2.0 km，東西長為4.7 km，井田面積為9.4 km2，井田內含煤地層主要是山西組和太原組。山西組主要有2層煤(2號煤層和3號煤層)，2號煤層為部分可采煤層，3號煤層為穩定可采煤層，山西組煤層平均厚度為2.0 m，含煤系數為6.0%。太原組主要有9層煤，5號和9號煤層為較穩定部分可采煤層，其他為不可采煤層，太原組煤層平均厚度為3.2 m，含煤系數為3.0%。研究煤層為3號煤層，平均埋深為600 m，煤層厚度為1.0～3.5 m，平均厚度為2.0 m，3號煤層距離2號煤層13 m左右，3號煤層結構簡單，其頂底板均為砂質泥巖和泥巖。

2 錨網強度耦合分析

在巷道圍巖控制技術中，護網將受到的承載力分布到錨桿上，隨著錨桿預緊力、強度、直徑、長度和托盤的規格的增大，錨桿的支護范圍也逐漸增大，但是仍會出現錨空區，此時需要護網對錨空區圍巖提供支持。當錨空區圍巖出現破落時，破落的圍巖會對網片施加載荷，網片受到施加載荷后，會出現網兜現象。根據靜力平衡原理，圍巖直接接觸的兩段網絲和破碎圍巖向網片施加的載荷在豎直方向的合力相同[4-5]。計算公式：

Pr=2Tr·sinβ

(1)

(2)

式中，Pr為破碎巖石所受的重力；Tr為AB段網絲或CD段網絲所受的拉力；β為金屬網的下沉角；H為網片的下沉量；a為網兜前原網絲長度的1/2。

如果網絲的軸向拉應變為ε，則：

(3)

式中，E為網絲材料的彈性模量；ε為網絲的軸向拉應變；S為橫截面積；δ為拉應力。

將式(2)、式(3)代入式(1)進行推導，得出：

(4)

由式(4)可知，金屬網下沉角和破碎巖石重力、網絲的彈性模量及網絲的橫截面有密切的關系。增加網絲的橫截面積、直徑以及彈性模量，可以提升網片的護表功能，從而使網片的護表效果更好。

當金屬網規格和錨桿間排距相同時，此時網片中心所受的載荷應力為最大，則網片提供的承載力F為：

(5)

式中，βm為網絲下沉角。

3 錨網支護下圍巖變形規律數值模擬

3.1 模型建立

為了研究錨網支護條件下圍巖變形規律，采用FLAC3D數值模擬軟件[6-10]，建立數值模型，模型尺寸為42 m×42 m×50 m。巷道圍巖參數：內摩擦角為30°，黏聚力為8×105MPa，彈性模量為2.8×104MPa，泊松比為0.3，抗拉強度為2.1 MPa，抗壓強度為55.5 MPa。

本文分別模擬分析3種方案：①方案1，無支護；②方案2，錨桿+菱形金屬網支護；③方案3，錨桿+格賓金屬網支護。

3.2 模擬分析

3.2.1 巷道塑性區分布

不同方案條件下巷道塑性區分布如圖1所示。

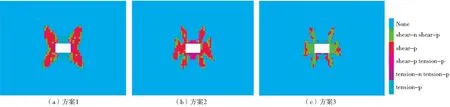
圖1 不同方案條件下巷道塑性區分布Fig.1 Distribution of plastic zone in roadway under different scheme conditions

由圖1可知，方案1條件下，由于巷道無支護，巷道四角的塑性區范圍較大，巷道塑性區呈“蝴蝶型”；方案2條件下，巷道兩幫的塑性區仍很大，塑性區呈“螃蟹型”，但是比方案一塑性區范圍縮小了19%，表明錨桿+菱形支護起到了一定的支護作用，但是金屬網沒有起到有效的主動支護作用；方案3條件下巷道塑性區形狀和方案2條件下巷道塑性區形狀相同，此時塑性區比方案1塑性區范圍縮小了10%，兩幫的塑性區也有明顯的改善。

綜上分析，錨網支護可以改善圍巖原有塑性區分布，降低巷道所受的圍巖應力，減小圍巖的塑性區范圍，起到了有效的支護作用；錨桿+格賓金屬網支護比錨桿+菱形金屬網支護效果更佳。

3.2.2 巷道圍巖應力分布

不同方案條件下巷道水平應力分布如圖2所示。

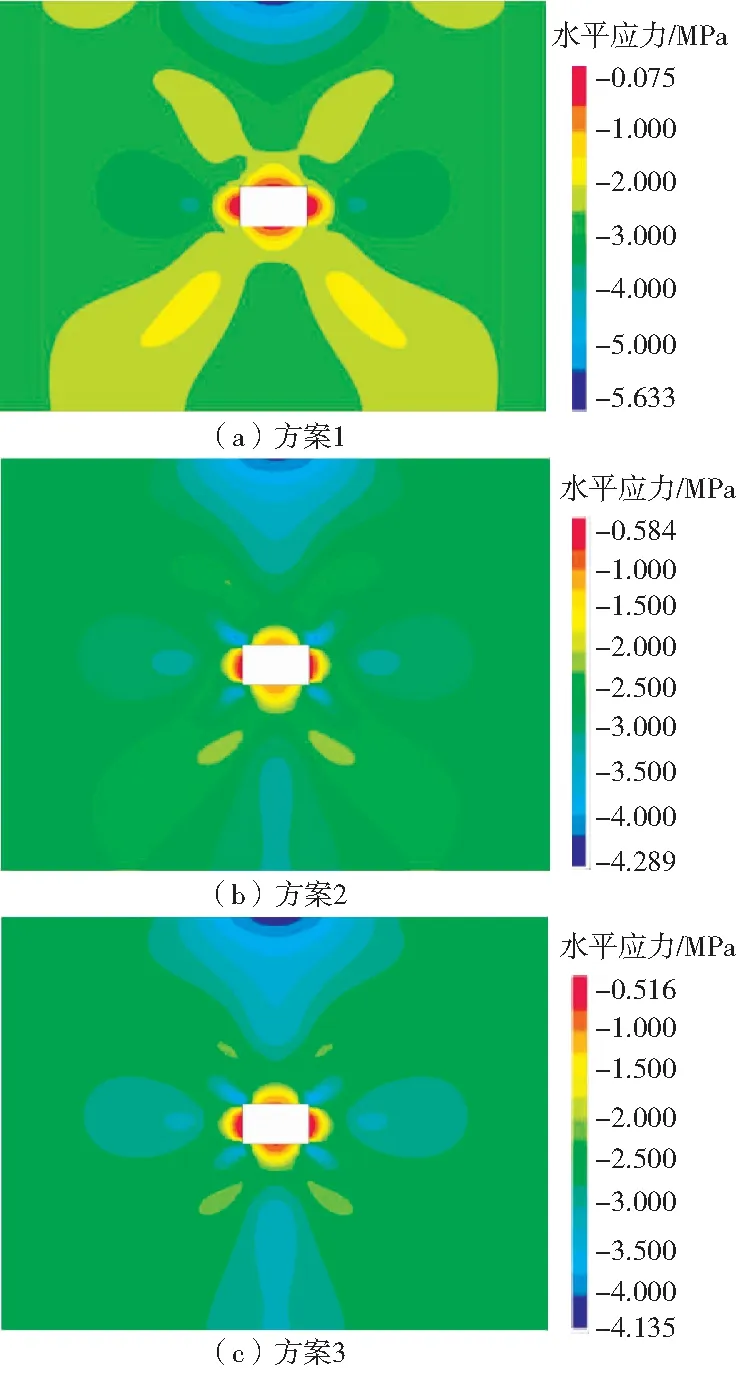
圖2 不同方案條件下巷道水平應力分布Fig.2 Horizontal stress distribution of roadway under different scheme conditions

由圖2可知，在方案1條件下，巷道頂板出現了應力集中區，應力峰值為5.7 MPa，巷道兩幫的最大水平主應力為1.9 MPa，頂底板最大水平主應力為1.6 MPa；在方案2條件下施加了錨網支護，巷道圍巖應力逐漸減小，在頂板的最大應力值為4.3 MPa，巷道兩幫的最大水平主應力為0.9 MPa，頂底板最大水平主應力為1.0 MPa；在方案3條件下，巷道圍巖應力進一步減小，在頂板的最大應力值為4.0 MPa，巷道兩幫的最大水平主應力為0.5 MPa，頂底板最大水平主應力為0.8 MPa。

綜上分析，采用錨網支護可以有效改善巷道圍巖應力，且采用錨桿+格賓金屬網支護后，巷道兩幫受到的水平應力和頂底板垂直應力都有顯著改善。

3.2.3 巷道圍巖位移情況

不同方案條件下巷道水平位移分布如圖3所示。

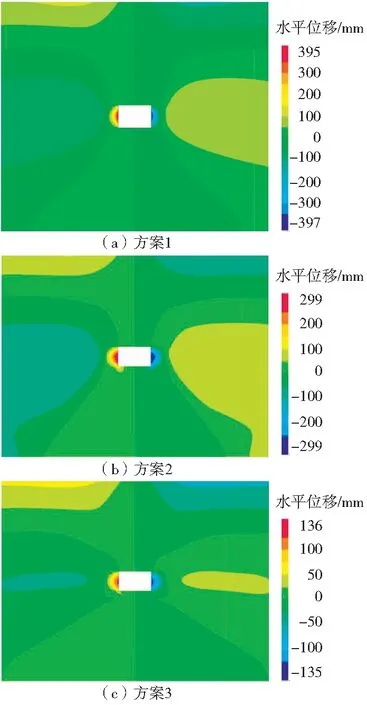
圖3 不同方案條件下巷道水平位移分布Fig.3 Distribution of horizontal displacement of roadway under different scheme conditions

由圖3可知，在方案1條件下，巷道處于無支護狀態，巷道兩幫最大的變形量為420 mm；在方案2條件下，巷道處于錨桿+菱形金屬支護狀態，巷道兩幫最大的變形量為280 mm；在方案3條件下，巷道處于錨桿+格賓金屬網支護狀態，巷道兩幫最大的變形量為130 mm。

綜上分析，采用錨網支護可以有效改善巷道圍巖變形，采用錨桿+格賓金屬網支護后，巷道兩幫變形和頂底板垂直變形都有顯著改善。

為了精確分析開挖后巷道水平和垂直位移量，在巷道的兩幫和頂板設置了測站，測站距離為5 m，總共有9個測試斷面，得到了3種支護條件下巷道位移曲線，如圖4所示。

圖4 3種支護條件下巷道位移曲線Fig.4 Roadway displacement curves under three supporting conditions

由圖4可知，當進行錨網支護后，巷道圍巖位移得到有效的改善，并且采用錨桿+格賓金屬網支護后，巷道護表效果明顯，能夠有效抑制巷道變形。

4 結論

(1)通過理論計算可知，增加網絲的橫截面積、直徑以及彈性模量，可以提升網片的護表功能，從而使網片的護表效果更好；錨網支護的強度耦合標準為網片具有足夠的強度來承載錨空區的圍巖重力。

(2)通過數值模擬分析可知，錨網支護可以改善圍巖原有塑性區分布，減小圍巖的塑性區范圍，錨桿+格賓金屬網支護比錨桿+菱形金屬網支護效果更佳；采用錨網支護可以有效改善巷道圍巖應力及圍巖變形；采用錨桿+格賓金屬網支護后，巷道兩幫受到的應力和變形量都有顯著下降。