接觸式輪廓儀的自動標注

四川信息職業技術學院 基礎教育部 四川 廣元 628017

一、問題的背景

接觸式輪廓儀的工作原理,利用探針和傳感器檢測被測的工作表面,以此來感受工件表面的幾何變化,在不同的方向采集信息并轉換成電信號,再經過處理之后轉換成數字信號且儲存在文件中。但由于接觸式輪廓儀存在探針污染、探針缺陷和掃描位置不準等問題,檢測到的輪廓曲線呈現粗糙不平的現象,這給工件形狀的標注帶來影響。基于此本文研究了如下兩個問題：

問題：當工件水平放置時,根據工件輪廓線上點的所有測量數據(xi,zi)(其中xi表示測量點的橫坐標,zi表示測量的縱坐標),求出工件輪廓線的各項參數值,即槽口寬度、圓弧半徑、圓心間的距離、圓弧長度、水平線段的長度、斜線線段的長度、斜線與水平線間的夾角和人字形線的高度。工件輪廓如圖1。

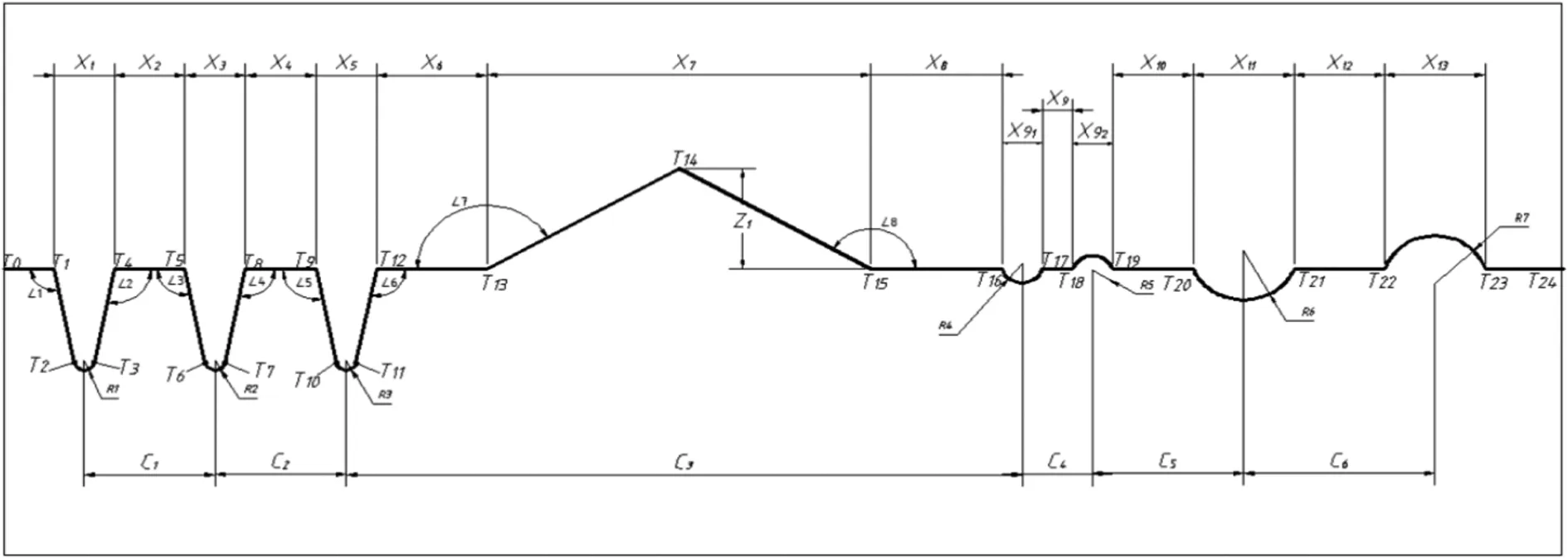
圖1

二、問題的解決

1.假設：對于以上問題的研究可以先作出假設,根據圖1我們作一些簡單的假設：(1)工件1輪廓的弧線段與其相交的斜線段相切；(2)工件輪廓的這些水平線段處在同一水平線段上；(3)假設工件被測時不會發生側移,及只在豎直平面內發生旋轉或平移。通過查閱資料,可以看出這些假設是合理的。

2.符號說明：對文章中所要用到的符號進行說明。為了清晰起見,我們把所有要用到的符號分兩批放置在圖中,在繼承圖1所示符號的情況下,再添加新的符號。

1.X1,X3,X5,X11,X13(也歸為槽口)表示工件槽口的寬度；

2.X2,X4,X6,X8,X9,X10,X12表示工鑒水平輪廓線段的長度,X7表示人字形的寬度；

3.∠i,i=1,…,8表示斜線段與水平線段的夾角；

4.ci,i=1,…,6表示各個相鄰圓弧段圓心之間的水平距離；

5.Ri,i=1,…,7表示各個圓弧對應的半徑；

6.Z1表示人字形線的高度；

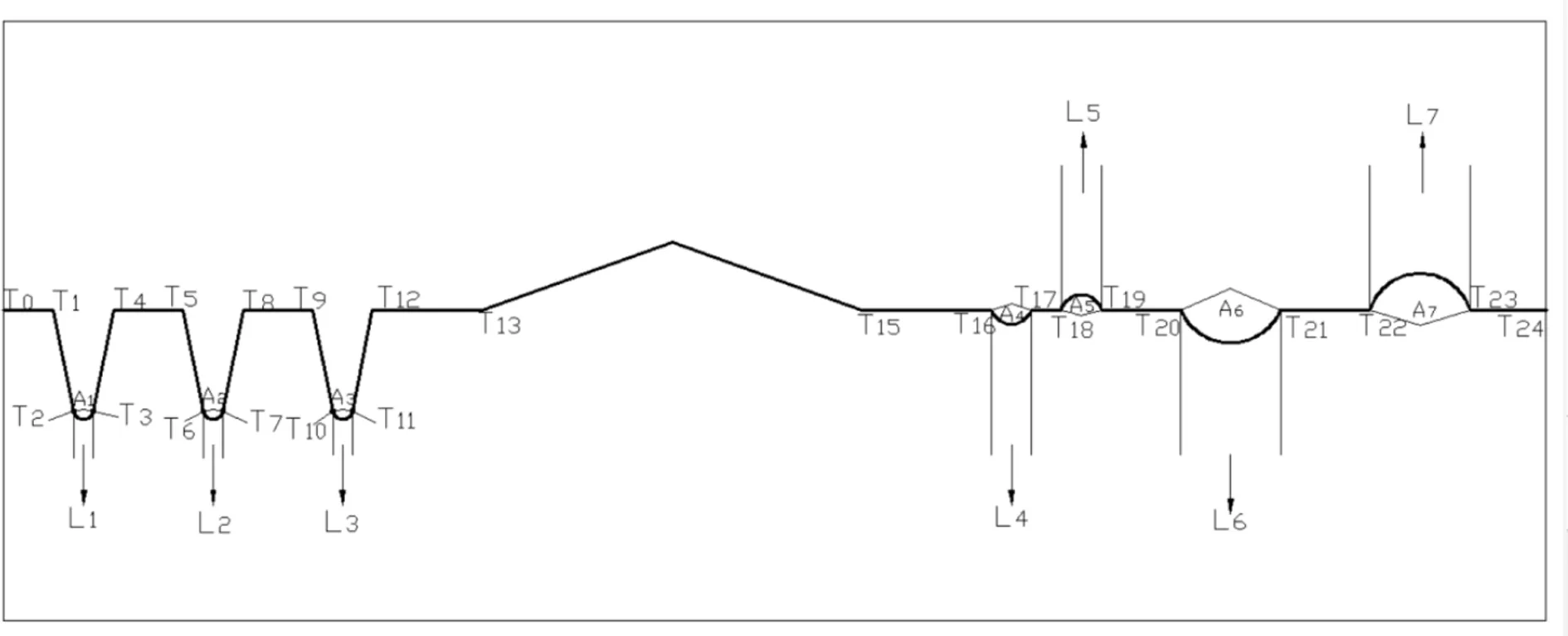
圖2

7.如圖2Ti,i=1,…,23表示各各區段的交點,其坐標用(xTi,yTi)表示,i=1,…,23,T0,T24分別表示工件的前后端點；

8.Ai,i=1,…,7表示各弧線段所對圓心角的大小；

9.Li,i=1,…,7表示各圓弧的長度；

10.Si,i=1,…,8表示斜線段的長度。

3.問題的建模與求解

問題1

(1)建模思路：建立平面直角坐標系,以輪廓儀的零刻度為坐標原點,那么輪廓線上測量各點的坐標即為此平面直角坐標系中的坐標。如此,工件的輪廓線即為某分段函數的圖像,若根據數據擬合出分段函數的函數解析式(如圖3),那么題中的各個參數值也就可以得出。

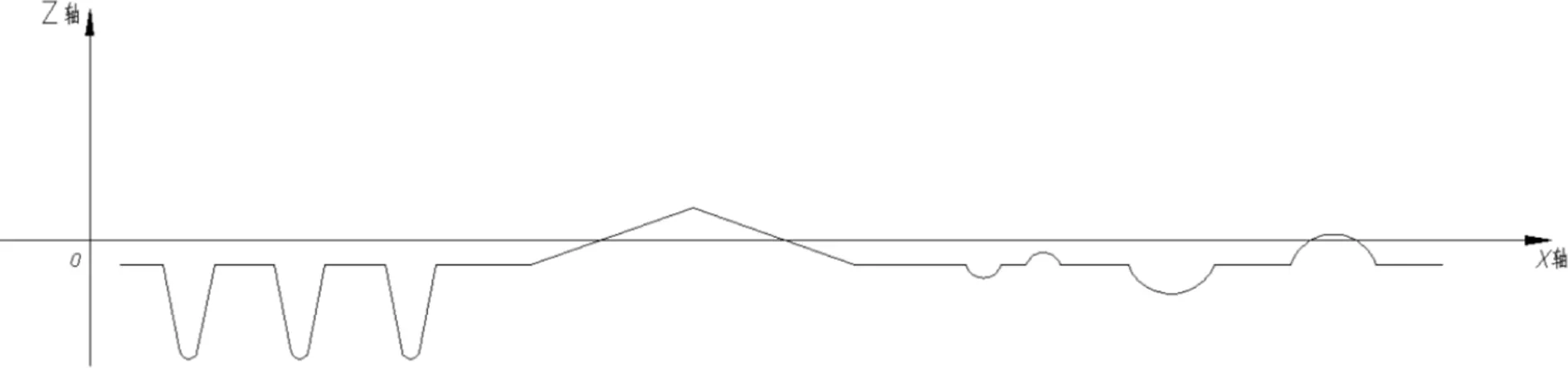
圖3

(2)模型的建立

1)從圖1可以看出,水平線段T0T1,T4T5,T8T9,T12T13,T15T16,T17T18,T19T20,T21T22,T23T24處于同一水平線,其函數可以設為z=C(C為常數)；

2)順次設8個斜線段T1T2,T3T4,T5T6,T7T8,T9T10,T11T12,T13T14,T14T15的函數解析式為：z=kix+bi,其中i=1,…,8為從左往右的斜線段的順序數；

3)順次設6個圓弧段T2T3,T6T7,T10T11,T16T17,T18T19,T20T21,T22T23的方程為：

4)根據各區段的函數解析式,可以得出各區段交點Ti的坐標(xTi,yTi),那么對于各參數,我們有如下的計算公式：

槽口寬度：X1=xT4-xT1,X3=xT8-xT5,X5=xT12-xT9,X11=xT21-xT20,X13=xT23-xT22；

水平線段的長度：X2=xT5-xT4,X4=xT9-xT8,X6=xT13-xT12,X8=xT16-xT15,X9=xT18-xT17,X10=xT20-xT19,X12=xT22-xT21；

圓心之間的水平距離：c1=xc2-xc1,c2=xc3-xc2,c3=xc4-xc3,c4=xc5-xc4,c5=xc6-xc5,c6=xc7-xc6；

人字形的高度：Z1=yT14-C；

斜線線段長度：可由兩點間距離公式求出

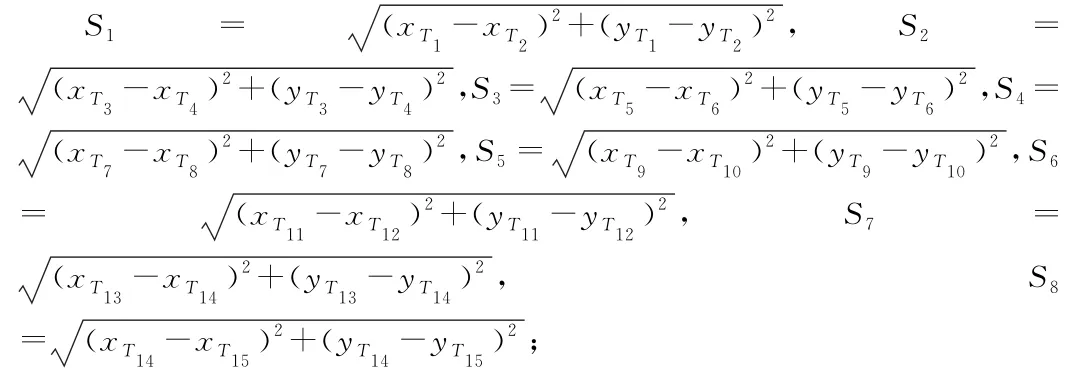
斜線與水平線的夾角：從圖中可以得出,這些夾角全為鈍角,因此所有的角可以由如下同一形式的公式得出∠i=π-arctan|ki|,i=1,…,8。

圓弧的長度：欲求圓弧的長度,先求圓弧所對圓心角大小,再根據弧長公式求得圓弧長,即圓心角A=180°+?+β,弧長。其中α,β分別表示弧線段左右兩邊斜線段與水平線所夾銳角。

(3)模型求解：對于以上模型的求解,我們主要分為如下步驟：

1)數據分區：根據實際情況我們可以知道,工件輪廓線的采點非常的密集,根據畫出所采點的散點圖,可以發現每個數據都有自己的所屬區段,先將數據按照區段劃分。但在按照區段劃分數據之時,因在各段交點不明確,那么在劃分各區段所包括數據的時候就會出現困難。因此,為了避免數據的區段劃分出現分歧,我們在理論上的交點附近合理刪除一些數據而不納入考慮范圍,那么剩下的數據我們認為是有明確的區段所屬。

2)水平線段的方程求解：對于水平線段的函數,我們用所有水平區段數據的Z值的平均值來求出。

3)斜線段的函數求解：在excel中利用斜線段所屬區段的數據擬合斜線段的函數z=kix+bi。

4)弧線段的方程求解：對于各個圓弧線段,利用已經處理的數據,參照最小二乘法擬合圓的公式：

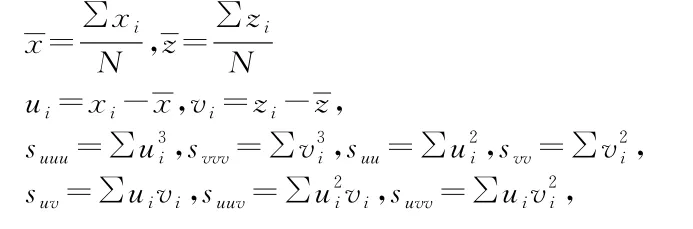
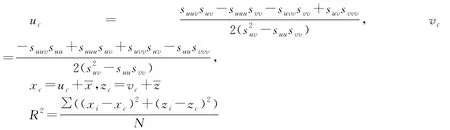
其中N表示數據的組數,xi,zi,i=1,…,N表示每組數據的橫縱坐標,(xc,zc)表示擬合圓的圓心坐標,R為圓的半徑。用此公式,可以得到各段圓弧的圓心、半徑。

5)各區段交點坐標求解：根據以上四步,用聯立函數解析式求解方程組可以求出各區段交點的坐標。但在此我們要說明的是,對斜線段與圓弧交點坐標的確定,不使用聯立函數解析式方程組的方法求解。事實上,在誤差存在的情況下,方程組很有可能出現無解的情況。因此,在假設斜線段與圓弧段相切的情況下,利用交點與圓心的連線垂直于斜線段求得斜弧交點。

6)交點求出之后,再根據模型建立中所示的各參數求解公式,可以求得各個所需參數。