基于局部薄盤光滑樣條函數的重慶地區氣溫空間插值

趙美艷，余 君，胡蕓蕓

(重慶市氣象信息與技術保障中心，重慶 401147)

早在19世紀，我國就有了現代方法的氣象觀測記錄，并逐步出現了較為完善的氣象數據[1]，但這些數據只是離散且不規則的氣象臺站數據，難以反映空間的連續變化特征。而站點外的數據一般由鄰近臺站的觀測值用一定的數學算法進行推算求得，插值算法便是利用已有的采樣點數據對未采樣點進行估算的一種數學方法，被廣泛應用于對連續空間的數值計算[2-3]。

插值算法的選擇是數據類型和計算效率的一種平衡，其中任何一種方法都不是絕對的[4]，只有特定條件下的最優[5]。近年來，用于氣象要素的空間插值算法有距離權重法(distance weighting)、克里格法(Kriging)、多項式插值法(interpolating polynomials)、Delaunay三角剖分線性插值、薄盤樣條法(spline methods)等[6-10]，但對于不同的變量所適用的插值方法不同[11]。在對多種插值方法進行對比分析時發現，基于地質統計技術的Kriging法和薄盤樣條法較為通用[12-13]。Collins[14 ]用多種插值算法對最高和最低氣溫進行了插值效果對比分析，認為在不同的時空尺度下，氣溫的插值誤差估計是不同的。馮錦明等[15]采用4種內插方法對中國160個臺站降水觀測資料進行空間插值結果分析，研究認為，臺站分布的密集度對插值方法的選擇有一定影響。對于不同變量，其“最優”內插法是相對的，而不是絕對的[16-19]。樣條法能夠有效優化數據逼真度和擬合曲面光滑度之間的平衡，具有不受空間尺度影響、不直接依賴空間平穩的協方差等優點；因此在綜合考慮誤差估計、數據結構及計算簡便時，使用樣條法進行氣候數據插值不失為一個好的選擇[14]。Hutchinson等[20]在利用經度、緯度和海拔高度之間線性關系的基礎上，提出局部薄盤光滑樣條插值算法[21-22]，并根據氣候要素插值的特點，設計編寫了針對氣候數據進行曲面擬合的專用軟件ANUSPLIN[23]。在ANUSPLIN軟件中允許引入多元協變量線性子模型，可以平穩處理二維以上的樣條，并且能同時完成兩個以上表面的空間插值，所以對于時間序列的氣象數據插值尤為適用。

在對氣象要素進行空間插值時，地形是影響誤差的一個重要因素。氣溫隨高度的上升而下降的現象具有普遍性且這種現象隨著時間和位置的不同而變化。重慶地處中國西南地區，地形以山地為主，且坡地面積較大，地形復雜，本研究將利用基于薄盤光滑樣條函數的曲面擬合程序ANUSPLIN，并依托數字高程模型(DEM)實現對重慶地區氣溫空間分布模型的建立。

1 數據與方法

1.1 數據來源

所用資料為重慶市氣象信息與技術保障中心提供的2017年12月31日21時至2018年12月31日20時重慶1 934個區域級自動站逐小時氣溫資料，均經過質量控制[24]。

1.2 臺站的選取

為了確保試驗數據的完整性和可用性，對1 934個自動站進行了篩選，選取原則和步驟如下。

(1)柵格挑選。將研究區域(28°N～32.2°N、105°E～110.2°E)按經緯度每0.05°×0.05°為一個柵格進行劃分。若一個柵格里僅有一個站，則選取該站；若此柵格里有2個以上的站點，則進行下一步挑選。

(2)計算所有臺站的氣溫平均可用率和各臺站的氣溫可用率，對柵格內的站點按可用率進行排序，選取臺站可用率大于平均可用率的站點；若柵格中沒有大于平均可用率的站點，則挑選數據可用率最高的一個站點。

(3)計算所有臺站的氣溫平均標準差和各臺站的氣溫標準差，對柵格內的站點按標準差進行排序，選取標準差小于平均標準差的站點，若柵格中沒有小于平均標準差的站點，挑選標準差值最小的一個站點。

在滿足條件(2)或(3)的臺站中，本研究最終選取了數據可用率達99.9%以上且標準差值相對較小的1 000個站點進行網格化試驗。

1.3 數字高程模型

數字高程模型(digital elevation model，下簡稱“DEM”)，它是用一組有序數值陣列形式表示平面坐標(x，y)及其海拔高度(z)的一種實體地面模型，主要描述區域地貌形態的空間分布，一般采用連續等間距的海拔高度點反映地形的變化。氣象要素插值的地形效應和空間尺度通常是通過與DEM結合來實現的，因此，擁有合適的空間尺度的DEM是構造氣象要素空間分布的基礎。本文采用1/20經緯度(約5 km)作為插值要表達的空間尺度而建立與之相對應的DEM。地形數據來自1∶5 000 000世界數字地圖。投影方式選用Albert投影。投影范圍為28°N～32.2°N，105°E～110.2°E(重慶范圍)。

1.4 曲面擬合

局部薄盤光滑樣條法在包含普通樣條自變量的基礎上，允許加入線性協變量子模型，所以它是薄盤光滑樣條原型的一個擴展[25]。如它對氣溫插值時，可以引入海拔高度等。局部薄盤光滑樣條理論統計模型如下

zi=f(xi) +bTyi+ei(i=1,…,N)，

(1)

式中，zi是位于空間i點的因變量，xi是樣條獨立變量的d維向量，f是關于xi的平滑函數，yi是獨立協變量P維向量，ei是隨機誤差。當式中缺少第二項，即模型無協變量時，該模型就變為一個普通的薄盤光滑樣條模型。當缺少第一項獨立自變量時，模型便變為一個多元線性回歸模型。

最早的擬合程序通常需要至少兩個獨立樣條變量，(即f(xi) 中i為2維矩陣)，一般是經度、緯度(以度為單位)。但是在擬合氣溫或降水量時，可增加第三個獨立變量，即海平面以上的高程(海拔高度)。在擬合多變量氣象表面時，只需知道樣點處的獨立變量的值，因此，氣象站點的坐標和海拔信息必須準確。坐標或海拔信息錯誤的點會在輸出的最大殘差日志里反映出來，即以降序排列的殘差文件中，排在首位的幾個極大殘差值對應的站點，可用于檢驗原始數據在位置和數值上的錯誤。

ANUSPLIN在插值過程中逐步迭代產生一系列統計參數，用來判斷插值效果。如表征擬合曲面復雜程度的信號自由度Signal值需小于站點數的一半，且在以月為單位進行曲面擬合時，Signal值應有較平穩的月間過渡；廣義交叉驗證GCV(generalized cross validation)估算插值誤差是通過移去一個站點，用剩余站點進行曲面擬合時得到該點的估算值，從而計算該點原始觀測值與估算值之間的誤差；GCV的平方根(RTGCV)是由輸入數據誤差和估算誤差組成，在模型選取時，應確保RTGCV是最小的；期望真實均方誤差(RTMSE)是所有樣點的預計均方根誤差的估算，相當于插值過程的真實誤差，同樣要選擇RTMSE值最小的模型；另外，RTGCV和RTMSE的差值越大,可間接說明模型的解釋率越高。

1.5 獨立性檢驗

為驗證ANUSPLIN所選方案的插值精度，本文除采用ANUSPLIN自帶的統計誤差進行分析外，還將基于重慶范圍內未參與插值的35個國家級自動站，采用交叉驗證和相關分析兩種方法對插值結果進行精度檢驗。平均絕對誤差(MAE)和均方根誤差(RMSE)可以作為衡量估算值與真實值誤差的兩個重要指標，即MAE和RMSE值越小，表明插值效果越好。

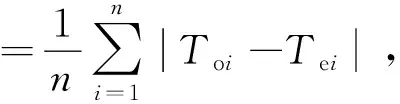
(2)

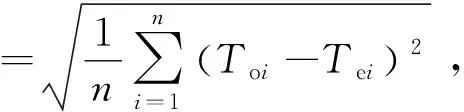
(3)

式中，n為臺站數，Toi和Tei分別表示第i個臺站的觀測值與估算值，同時，還計算了相關系數來反應臺站的估算值與觀測值之間的相關性。

2 結果與分析

2.1 插值表面分析

時間序列的氣象要素空間插值結果既要能保證插值表面的插值精度，又要保證所選插值模型的穩定性，使其在時間和空間的連續上具有可比性。為尋找合適的氣溫插值方案，本研究共設計了6種模型(表1)，即以高程數據為自變量或協變量，改變樣條次數。

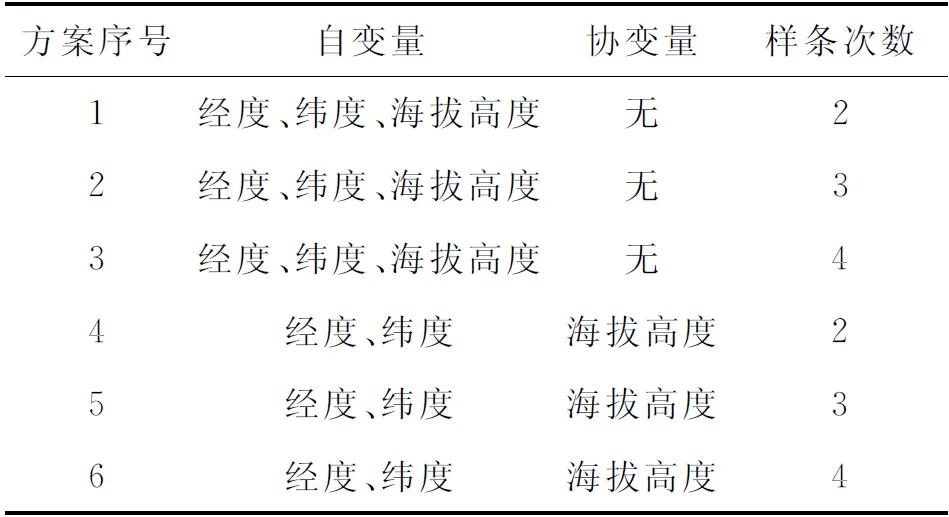
表1 薄盤光滑樣條函數模型

針對重慶市1 000個站點氣溫要素的空間插值，在參照模型判別標準的條件下，當Signal值小于站點數的一半時，選取模型最穩定，且GCV值最小的方案，經過反復試驗，最終確定以經、緯度為函數自變量，海拔高度為協變量，樣條次數為2的三變量局部薄盤光滑樣條函數。

圖1給出了2018年8月1日10時重慶的氣溫插值。從圖1a可以看出，插值表面帶有明顯的地帶性差異。就整個重慶來看，中西部氣溫明顯高于東北及西南地區，其中重慶東北部有一白色區域，氣溫明顯低于其他地區，主要因為這里海拔高度較高(2 500 m)，平均氣溫值比周邊低8～10 ℃。值得注意的是，在重慶中東部地區，有幾條明顯的條帶狀氣溫低值區，如梁平、墊江、萬州及忠縣等地，而這些帶狀低值區正好對應著明月山、精華山等山脈；因此從圖中可以明顯看出氣溫隨高度的梯度變化，這與常見的氣溫插值趨勢面不太一樣。從估算標準誤差(圖1b)可以看出，整個重慶的氣溫誤差均較小，誤差值基本在1.0 ℃以下，而重慶地區以外，誤差值逐漸增大。就重慶內部而言，東北及東南部的高海拔地區誤差比其他地區偏大0.1 ℃左右，因為高海拔區，站點相對較少，從而導致誤差稍大。

圖1 2018-08-01T10重慶氣溫插值(a)和估算標準誤差(b)(單位為℃)

由此可以看出，引用高程線性子模型的局部薄盤光滑樣條函數可以較好實現對氣溫的空間插值，且能實現對站點稀少的山脈地帶氣象要素的插值估算，而插值誤差因地形的差異會有不同表現，即站點稀少高海拔區相對于站點密集低海拔區，估算誤差較大。

2.2 統計結果分析

月平均氣溫的插值曲面統計分析結果見表2。從表中可以看出，信號自由度Signal值遠遠小于站點數的一半，由此可以說明試驗所用站點數能夠滿足插值的需求。氣溫插值的期望真實均方誤差RTMSE值除7、8月份大于0.2 ℃外，其余多數月份均小于0.2 ℃，且2018年各月RTGCV值的大小分布也表現出了秋冬季較小，夏季較高的分布形式。夏季，重慶中西部地區(低海拔區)高溫悶熱，氣溫高達40 ℃，而東部高海拔區的氣溫最高在30 ℃左右，氣溫的空間分布差異較大；冬季，重慶高、低海拔區的氣溫差異相對夏季來說則較小。由此可以看出，重慶復雜的地形(海拔差異較大)對氣溫空間差異的影響夏季較冬季明顯。

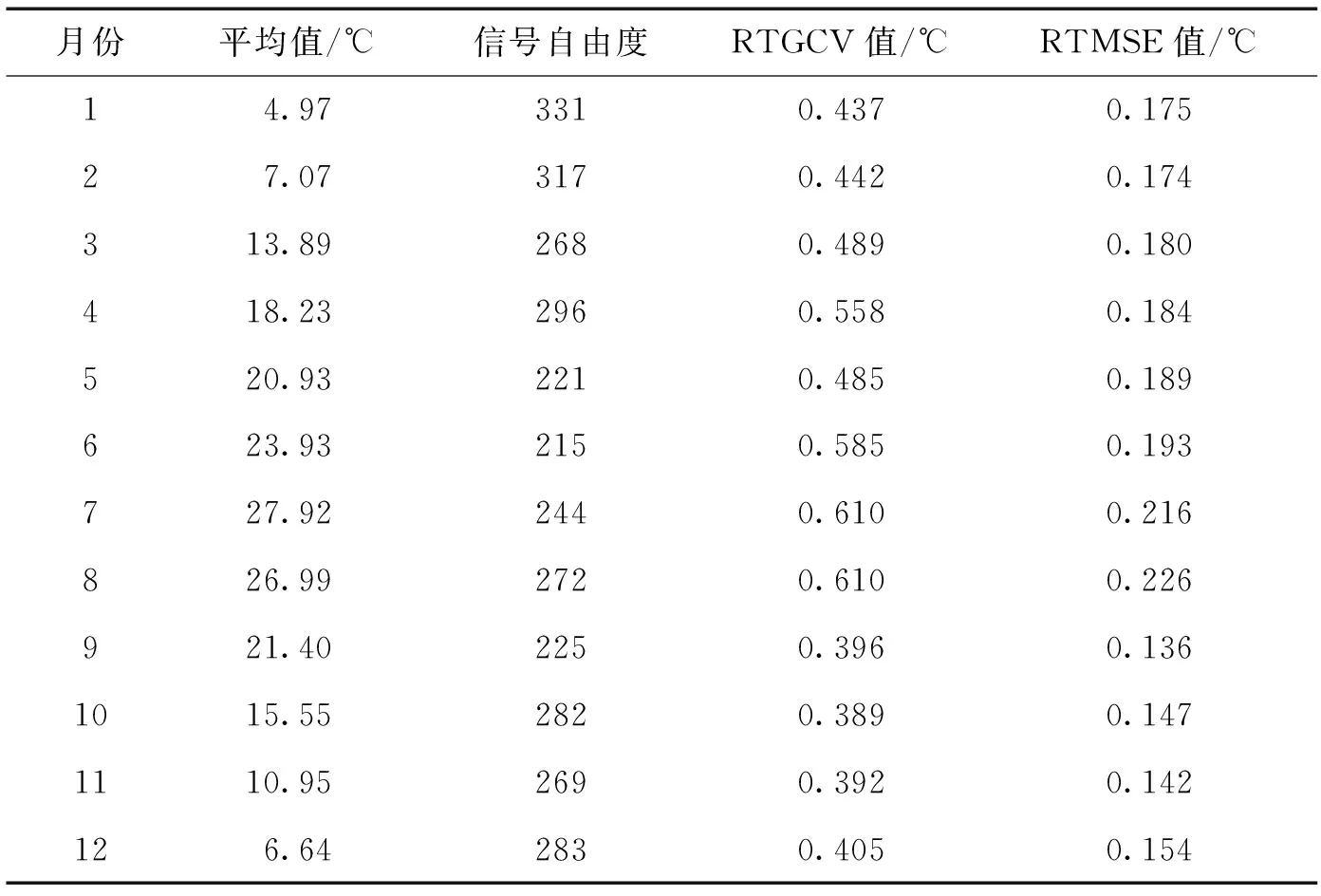
表2 2018年各月平均氣溫插值統計結果

由于模型中引入了第三變量，即海拔高度作為協變量，因此便存在一個隨高程變化的線性常數，ANUSPLIN在此提供了一個氣候變量隨海拔高度的變化率(lapse rate)。從圖2可以看出，氣溫隨海拔高度下降的幅度在夏季為0.6 ℃/100 m，春秋季較小為0.5 ℃/100 m左右，冬季最小，為0.4 ℃/100 m左右。由此可看出，不同的季節，氣溫隨海拔高度的變化率并不完全相同，這跟一些學者研究其他地方得出的結論相似[26]。

圖2 重慶氣溫隨海拔高度變化率的月際變化

2.3 獨立性檢驗

為了驗證模型所選插值方案對氣溫的插值精度，將重慶范圍內未參與插值的35個國家級自動站的氣溫觀測值與模型插值結果，求取平均絕對誤差(MAE)和均方根誤差(RMSE)(圖3)。整體上看，所用插值方案插值效果較好，月平均氣溫的MAE值為0.69 ℃，且冬季優于夏季，其中1月最小(0.60 ℃)，9月最大(0.85 ℃)。RMSE值隨時間的分布與MAE相似，冬季相對較小。雖然獨立檢驗的插值均方根誤差RMSE相對于模型本身計算的期望真實均方誤差RTMSE稍偏大(這或許跟模型考慮了地形因素有關)，但二者隨時間的分布特征相似。另外，插值月平均氣溫值與臺站觀測值的相關系數達到0.995，相關性較高。由此可以看出，本研究所采用的插值方案，即以經、緯度為函數自變量，海拔高度為協變量，樣條次數為2的三變量局部薄盤光滑樣條函數對重慶地區的氣溫插值較為適用。

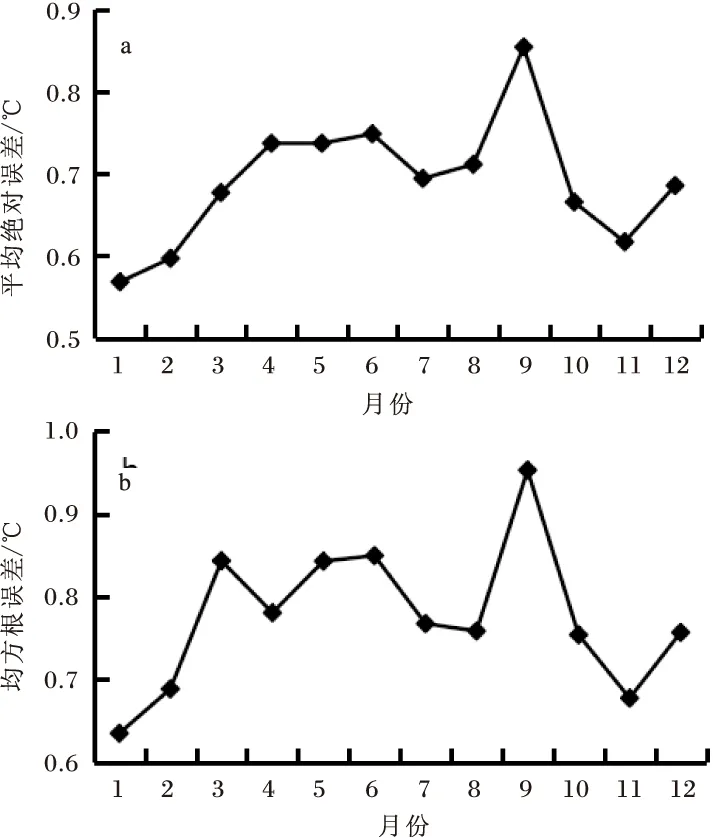
圖3 重慶插值氣溫的平均絕對誤差(a)和均方根誤差(b)

3 結論與討論

(1)利用薄盤光滑樣條函數的曲面擬合程序ANUSPLIN和依托數字高程模型(DEM)，以經、緯度為函數自變量，海拔高度為協變量，樣條次數為2的三變量局部薄盤光滑樣條函數作為插值方案，建立重慶地區氣溫要素的空間分布模型，實現了對重慶市1 000個站點氣溫的最優空間插值。

(2)從氣溫插值結果可以發現，插值方案實現了對站點稀少的高海拔區氣溫要素較為精確的插值估算，且插值表面能夠明顯看出氣溫隨高度的梯度變化，再現了地形因素對氣溫空間差異的影響在夏季較冬季明顯的特征。由此可以看出，研究所采用的方案對重慶地區的氣溫插值是適用的。