音圈電機直驅水液壓球閥的動態特性建模與仿真研究

張增猛，王 旭，楊 勇，陳英龍，田 昊

(大連海事大學 船舶與海洋工程學院，遼寧 大連 116000)

引言

直驅式電液伺服閥(Direct-Drive Valve，DDV)具有高頻響應、結構簡單等優點，是目前電液伺服閥的主要研究方向[1]。直驅式電液伺服閥在水液壓領域的應用亦成為了研究重點。為準確地控制純水液壓系統中的壓力或流量，直驅閥必須具有足夠的控制精度和動態品質[2]。

近年來隨著對環境友好性要求的提高，水液壓技術發展取得了持續增長，水液壓閥作為水液壓系統的核心原件，廣泛應用在煤礦水液壓系統和海洋機電液裝備中。國內外學者對水液壓閥及其關鍵技術進行了廣泛的研究。

劉曉鵬等[3]研制了一種音圈電機直驅高速水液壓開關閥，實驗結果表明直驅閥的流量可達100 L/min，在壓力8 MPa、電壓240 V的條件下，開啟時間為7 ms，關閉時間為9 ms，動態特性較好。毛燕語等[4]研制了一種旋轉式水液壓比例閥，建立了其數學模型，并對其動態特性特別是頻率響應進行了仿真研究。金銘[5]研制了一種伺服電機驅動式高壓大流量水液壓節流閥，仿真和試驗結果表明該閥具有較好的位置控制精度和動態特性。白瓊等[6]通過在Fluent中進行CFD仿真，分別研究了具有不同形式非全周閥口的水液壓滑閥的液動力特性，結果表明水液壓產生的液動力小于46#抗磨液壓油產生的液動力。MAJDIC F等[7]在水液壓三位四通滑閥閥芯上使用類金剛石涂層，循環壽命試驗結果表明，此方法減小了水潤滑條件下的滑閥摩擦力，改善了磨損和泄漏現象。周大偉[8]使用微造型技術改善了水液壓三用滑閥的磨損現象。

本研究基于已研制的音圈電機直驅水液壓球閥[9]，這是一種帶有閥芯位移閉環的節流閥；經實驗分析可知閥芯上各種作用力模型以及音圈電機模型不夠準確是限制其動態特性提高的原因之一，而精確地建模是提高靜態控制精度和動態響應效果的關鍵。對于閥芯上的作用力以及音圈電機模型，學者已進行了廣泛的研究。

陳幼平等[10]自研了音圈電機并建立了數學模型，為了獲取定量的黏性阻尼，對直線電機進行了自由振蕩試驗。YUAN Qinghui等[11]通過在Fluent中進行CFD仿真與試驗研究了四邊滑閥的穩態流體作用力，在分析滑閥流體作用力時使用了壓力積分法與動量法，并指出在研究液動力時應當考慮流體黏性的影響。陳春等[12]對水液壓伺服滑閥副之間的摩擦進行了實驗研究，結果表明，Stribeck模型能較好的描述水液壓滑閥副之間的摩擦力。

1 音圈電機直驅水液壓閥的結構與數學模型

1.1 結構分析

音圈電機直驅水液壓球閥的結構如圖1所示。當音圈電機不通電時，閥芯通過兩側的彈簧定位使閥芯緊靠在閥座上。閥的最大設計流量為20 L/min，最大設計壓力為4 MPa，閥芯位移為330 μm。流體由閥體6上的高壓腔P流過閥套組件4進入閥腔，經球閥閥口后流入低壓腔T，回到水箱。5為靜壓力平衡腔，可以平衡大部分的靜壓力。閥芯組件3由左推桿、球芯、右推桿組成；左推桿與音圈電機相連接，推動球閥閥芯與右推桿軸向移動，閥的出口流量與閥芯位移變化呈近似線性關系[9]。

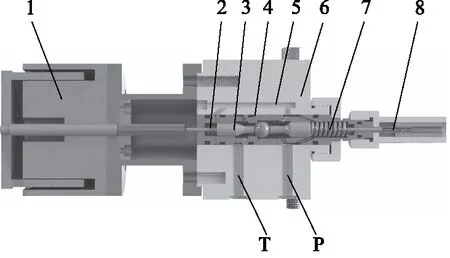
1.音圈電機 2.左彈簧 3.閥芯組件 4.閥套組件 5.靜壓力平衡腔 6.閥體 7.右彈簧 8.位移傳感器

1.2 數學模型

閥芯上的作用力如圖2所示，基于閥芯上的作用力關系建立閥芯動力學模型，如式(1)所示[13]：

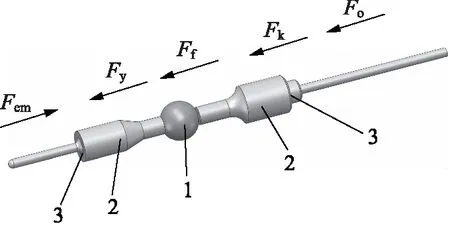
1.陶瓷球 2.密封面 3.彈簧座

(1)

式中，Fem—— 音圈電機輸出力

m—— 閥芯等效質量

x—— 閥芯位移

b—— 黏性阻尼系數

Ff—— 閥芯摩擦力

Fk—— 彈簧彈力

Fy—— 穩態流體作用力

Fo—— 密封圈阻力

1)音圈電機的數學模型

當音圈電機的結構和負載形式不同時，其數學模型也有差別[10]。本研究中將音圈電機動子的機械運動模型等效為一個單自由度的彈簧-質量-阻尼系統，如圖3所示。

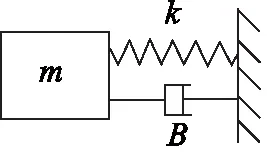
圖3 音圈電機等效模型

由音圈電機的力平衡方程、電壓平衡方程得到以x(t)為輸出，u(t)為輸入的音圈電機的微分方程進而拉氏變換得到音圈電機位移與控制電壓之間的傳遞函數為：

(2)

式中，L—— 線圈電感

m—— 線圈質量

R—— 線圈電阻

k—— 彈簧勁度系數

km—— 電機力常數

2)流體作用力特性

閥內的流體對閥芯產生的液動力與靜壓力的合力稱為流體作用力，流體作用力的存在影響閥的動、靜態特性，是閥的設計中需要著重考慮的因素[14]。使用動量法來計算穩態液動力，從而可由式(3)計算閥芯上的流體作用力：

Fpoppet=pAp+Fy=pAp+ρQvcosα

(3)

式中，Ap—— 靜壓作用面積

ρ—— 水的密度，取998.2 kg·m-3

Q—— 流量

v—— 流束最小斷面處的流速

α—— 流束方向與閥芯軸線的夾角，取45°

(4)

式中，A—— 閥口過流面積

Δp1—— 閥口前后的壓差

Cd—— 控制閥流量系數，取0.95[15]

帶入閥的參數，由動量法計算的穩態流體作用力數值如圖4所示，由圖可知，流體作用力隨著壓差和閥口開度的增大而增大，當壓差為3.5 MPa，開口為330 μm 時，流體作用力達到最大值24.69 N。

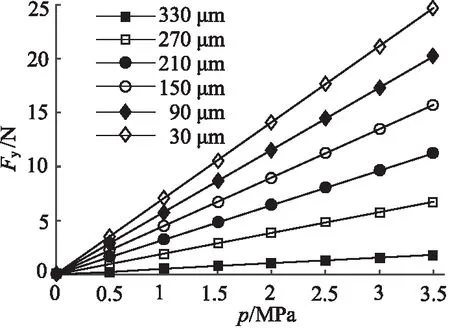
圖4 流體作用力數值

3)摩擦力模型

考慮閥芯與閥套之間的靜摩擦力與動摩擦力，按Stribeck模型有：

(5)

式中，FS—— 閥芯靜摩擦力

FC—— 閥芯庫倫摩擦力

vs—— Stribeck速度

σ—— 黏性摩擦系數

4)密封圈阻力模型

O形密封圈的材料為丁腈橡膠，由文獻[16]可知，其摩擦阻力可由式(6)計算：

(6)

式中，d—— 密封圈外徑

B—— 密封圈寬度

f—— 摩擦系數，取0.2[17]

ε0—— O形圈預壓縮量，本研究中為15%

E0—— O形圈的彈性模量

μ0—— O形圈的泊松系數

Δp2—— 密封圈兩端的壓差

根據以上分析，在Simulink中建立音圈電機輸入電壓與閥芯位移關系的模型，如圖5所示。

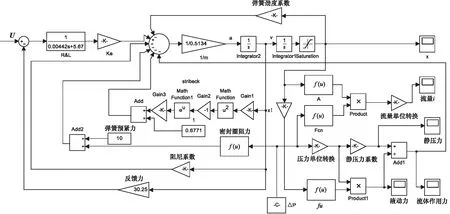
圖5 音圈電機直驅閥的模型

2 模型中的參數辨識

2.1 音圈電機黏性阻尼系數辨識

音圈電機的數學模型，其傳遞函數中的空氣阻尼系數B未知，為辨識阻尼系數，設計搭建了帶有彈性負載的音圈電機測試試驗臺，如圖6所示。

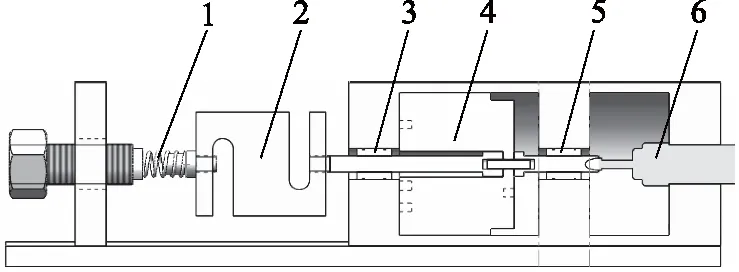
1.彈簧 2.力傳感器 3、5.直線軸承 4.音圈電機 6.LVDT傳感器

帶有彈性負載的音圈電機當外部作用力為0時，其力平衡方程為式(7)：

(7)

式中，m—— 運動部分質量

B—— 阻尼系數

k—— 彈簧勁度系數

將式(7)表示為典型二階常系數齊次微分方程如式(8)所示：

(8)

即：

(9)

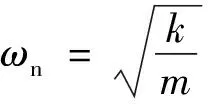
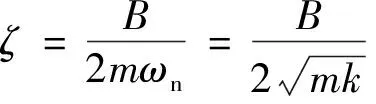
方程的左邊完全由參數m，B，k所決定，反映了系統本身的固有屬性；當電機進行初始振幅為A的自由振蕩，得到電機的衰減振蕩曲線方程式(10)：

x(t)=e-ntAcoskt

(10)

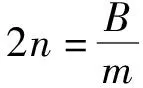
試驗中，使用信號發生器輸出正弦型號到功率放大器，功率放大器驅動電機實現振蕩運動，待振蕩穩定后，關閉信號發生器[18]，采集此時音圈電機位置信號隨時間變化的振動曲線，并使用MATLAB擬合振動曲線為式(10)形式，如圖7所示，辨識出空氣阻尼系數為10.96 N·s/m。

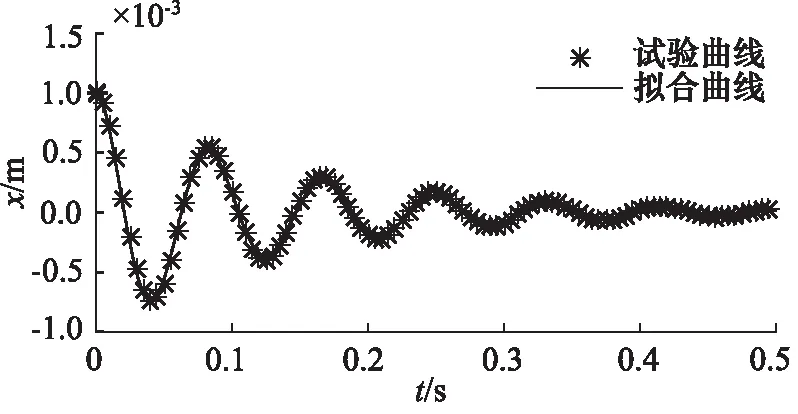
圖7 自由振蕩曲線的擬合

2.2 閥芯摩擦力測量

為辨識Stribeck模型的關鍵參數，搭建試驗臺如圖8所示，使用了步進電機帶動滾珠絲杠推動閥芯，通過調節步進電機到一固定轉速，就可以實現閥芯的勻速運動，此時不同運動速度下測量的軸向力就是閥芯與閥套之間的摩擦力。

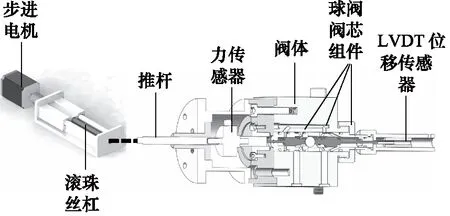
圖8 摩擦力測量試驗臺

將測量數值擬合為Stribeck函數，擬合結果如圖9所示；經過擬合曲線得到參數：FC=0.6771 N，FS=1.65 N，vs=0.1276 mm/s，σ=0.3488 N·s/mm。

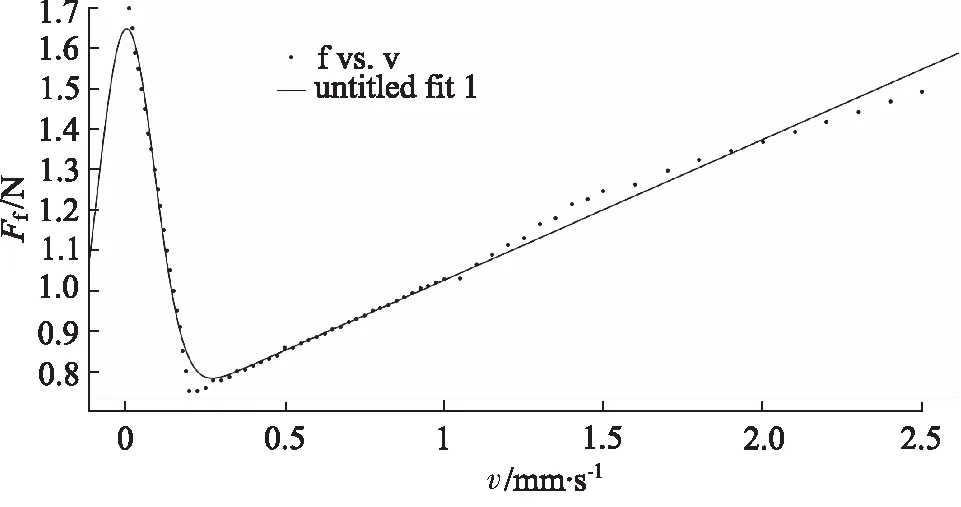
圖9 摩擦力測量數值與擬合

3 動態模型的仿真分析

3.1 階躍響應

通過辨識試驗完善了直驅閥的Simulink模型，得到了線圈電壓與閥芯位移之間的傳遞函數。

仿真時設置進出口壓差為0.5，1.0，1.5，2.0，2.5，3.0，3.5，4.0 MPa，音圈電機最高電壓輸入電壓為42.4 V，考慮到高壓環境下閥芯上的阻力較大，因此分別選取音圈電機的階躍電壓為15，20，25，30，35，40 V。圖10是穩態值的對比。圖11～圖13是選取了3組電壓值和3組壓差得到的階躍響應曲線。

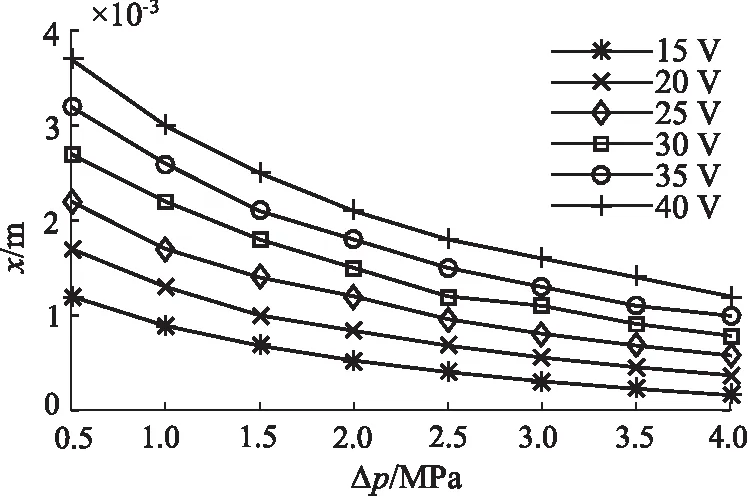
圖10 閥芯位移的穩態值

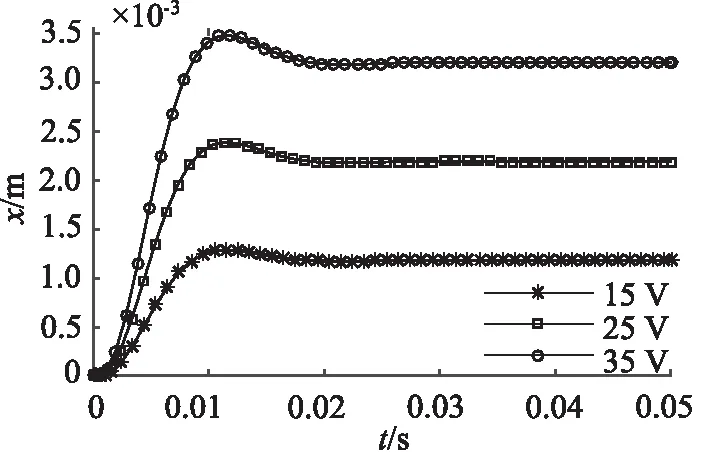
圖11 壓差為0.5 MPa時的階躍響應

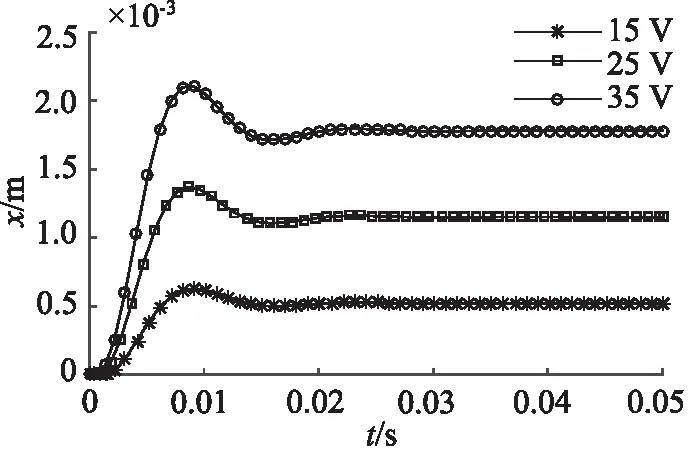
圖12 壓差為2 MPa時的階躍響應

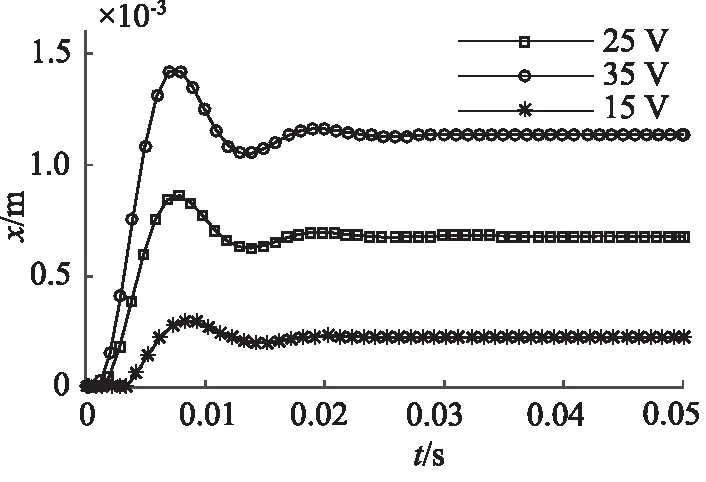
圖13 壓差為3.5 MPa時的階躍響應

由圖可知：

(1)穩態值隨著階躍電壓的增大而增大，隨著進出口壓差的增大而減小。當壓差為3.5 MPa、階躍電壓為15 V時，穩態值最小為0.2234 mm；當壓差為0.5 MPa、階躍電壓為25 V時，穩態值最大為2.196 mm；

(2)調整時間隨著壓差增大而增加，隨著階躍電壓的增大有略微減小的趨勢。當壓差為0.5 MPa、階躍電壓為15 V時，調整時間最小為0.01654 s；當壓差為3.5 MPa、階躍電壓為25 V時，調整時間最大為0.02225 s；

(3)閥芯位移的超調量隨著壓差增大而增大，隨著階躍電壓增大幾乎沒有變化。當壓差為0.5 MPa時，超調量最小為1.08%；當壓差為3.5 MPa時，超調量最大為1.32%；

(4)上升時間隨著壓差的增大而縮短，隨著階躍電壓的增大而縮短。當壓差為0.5 MPa、階躍電壓為15 V時，上升時間最長為0.00854 s；當壓差為3.5 MPa、階躍電壓為25 V時，上升時間最短為0.00533 s。

同時，壓差增大，電機力需要補償的軸向力越大，在圖12、圖13中階躍響應曲線剛開始階段位移為0反應了這一現象。

3.2 頻率響應

本研究中直驅閥因為定位彈簧和密封圈的存在，音圈電機需要先抵消彈簧預緊力和密封圈的阻力才能推開閥芯，所以正弦響應的電壓區間設置為6～16 V，頻率為10 Hz，響應曲線如圖14所示。由圖可知，壓差為0.5 MPa時，正弦響應幅值為1.016 mm；壓差為1 MPa 時，正弦響應幅值為0.847 mm；壓差為1.5 MPa時，正弦響應幅值為0.725 mm；隨著壓差的增大，正弦響應的幅值變小。

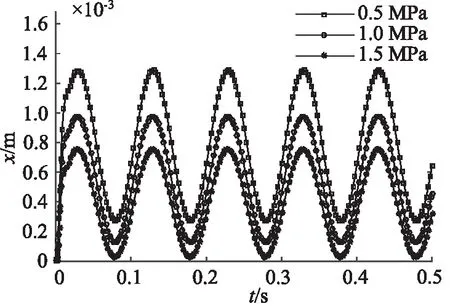
圖14 壓差對頻率響應的影響

4 結論

本研究基于閥芯上的作用力關系建立了音圈電機直驅水液壓球閥的數學模型，同時在Simulink中建立了直驅閥的仿真框圖，并進行了仿真分析。從仿真結果可以看出，當進出口壓差不變時，直驅閥的閥芯位移與線圈電壓幾乎呈線性增大的關系，同時階躍電壓的增大使閥芯振蕩過程更明顯、調整時間更長。

從建模方法上看，建模過程考慮了音圈電機黏性阻尼、閥芯摩擦力、流體作用力等非線性因素，相比傳統的線性分析方法存在受非線性因素限制和狀態變量較多等問題，具有一定的全面性。并且精確模型的建立方便后續直驅閥線圈電流、閥芯位移雙閉環控制設計的開展。