數學建模計算空間路徑的方法在爬電距離和電氣間隙測量中的應用

汪奕帆 馮秉佑

（嘉興威凱檢測技術有限公司 嘉興 314000）

引言

在電器產業不斷發展的現階段，各類產品的安全性能已經被越來越多的人所重視，而不同產品的多樣性和獨特性，又使得確定并測量爬電距離和電氣間隙的“最短”路徑，變得尤為困難。本文以實際樣品來舉例，分享一種需要空間橋接的復雜爬電距離問題的解決方案。

1 案例分析

由于爬電距離和電氣間隙不符合標準要求而發生的安全事故屢見不鮮，其中最為著名的要數2016年三星手機著火事件，據公開調查結果顯示，主要問題來自于采用的SDI電池（圖1）。

圖1可以清晰的看到，在外部引起電池電極變形后，導致了電池電極之間的爬電距離和電氣間隙減小到安全限值以下，引起電池短路，從而導致了著火事件的發生[1]。

可見，確定產品絕緣結構的組成、導電部件和易觸及表面，選取正確的爬電距離和電氣間隙的路徑，并用適合的測量設備確定數據，是取得準確檢測結果和防止誤判的關鍵，而其中最短路徑的確定則是重中之重。

2 實際舉例計算

對于簡單的案例我們可以通過直接測量或者簡單的展開平面、幾何計算，就可以得到相應的爬電距離，但是當實際樣品爬電距離需要經過幾個面，甚至可能需要空間橋接時，簡單的測量、計算已經無法滿足我們的要求，下文就以能力驗證中的樣品來舉例，借用一種先建立三維模型，再建立數學模型，最后引入編程計算機計算的思路，重點探討如何逐步的分析、計算需要空間橋接的復雜爬電距離問題。

2.1 樣品簡述

本次試驗的被測樣品為印刷電路板（雙面板），如圖2和圖3。

其中： T1、T2、T3、T4為印刷電路A面的電極，R1、R2為印刷電路B面的電極，中間梯形的區域鏤空。

本樣品在測試中有如下特殊說明和假定：

①樣片中梯形鏤空區域的角全部按“尖角”考慮，不視為圓角，∠α=90 °。

②在電氣間隙、爬電距離測量時，樣片中電極T3、T4、R1、R2與梯形鏤空區域邊緣按“齊平”考慮。

③爬電距離和電器間隙測量值精確到0.001 mm。

2.2 爬電距離電氣間隙的影響因素

爬電距離電氣間隙影響因素有很多，如：海拔高度，電場條件，污染等級，橋接（跨接），通過中介物（如有的話）等都會對爬電距離和電氣間隙產生不同程度的影響。此例中著重考察污染等級和橋接（跨接）。

污染等級：爬電距離和電氣間隙極易受到外來物質污染的干擾，確定污染等級對測量爬電距離和電氣間隙非常重要。

圖3 樣品B面

橋接（跨接）：在電器的長期使用過程中，如灰塵、其它導電微粒會積累在污染絕緣材料表面，導致沿污染物表面形成爬電路徑，所以在小尺寸的“間隙”和一定角度下的“槽”，需要著重考慮橋接問題[2]。

2.3 對于實例的分析和思路

試驗過程中，最為復雜的部分要屬T1與R1中金屬部件之間的爬電距離的路徑及測量值（2級污染等級和3級污染等級均需測量）。由于T1-R1之間不在同一個平面上，也不能通過簡單的展開處理將T1和R1放到同一平面上，這讓求解這個爬電距離問題變得復雜了許多。

2.4 三維建模

我們通過三維軟件UG進行建模（圖4），建立等尺寸的模型有利于我們更好的觀察樣品，從而分析和尋找最短路徑。

2.5 分析路徑

通過模型分析，可以得到爬電距離的路徑只可能存在3種情況（圖5）。

①圖5中T1-E-R1路線。

此路徑爬電距離可以直接在樣品上測得路徑為：23.649 20≈ 23.649。

②圖5中T1-（EH線段上的某點K1）-I-R1路線。

此路徑爬電距離看似不能直接測得，實際上可以將T1-H-E沿著HE展開，使得T1,H,E,G,I在同一平面，此時兩點之間線段最短，路徑T1-（EH線段上的某點K）-I-R1轉變為T1-I- R1，再通過簡單的幾何計算得到路徑為：25.033 25≈25.033。

③圖5中T1-（EH線段上的某點K）-（EI線段上的某點O）-R1路線。

此時需要考慮是否橋接問題。

2.6 考慮橋接問題

根據DSH-590號TCL決議單80 °角規則（溝槽橋接規則）：如果V型溝槽頂角大于80 °其爬電距離應沿著槽的輪廓進行繪制（圖6）；如果V型溝槽頂角小于等于80 °，且開口寬度大于短接尺寸“X”，其爬電距離應沿著槽的輪廓進行繪制，但槽底用短接尺寸為“X”的連接跨接（圖7）[3]。（2級污染等級X=1.0 mm和3級污染等級X=1.5 mm）。

由于標準IEC 60664-1和TCL決議590中只是對平面橋接進行定義，而此處可能涉及空間橋接的最短爬電距離問題，所以筆者認為簡單的以面面夾角∠H1EH2<80 °即認為滿足橋接條件是不合理的。

由模型可知爬電距離的最小路徑必定存在，所以我們先假設通過空間橋接AB（圖9中）最短路徑在T1-KA-B-R1（圖9中路線）取得，最后我們再驗證最短路徑時，在跨接點已知的情況下，如果不橋接所形成的最短路徑夾角是否＜80 °，如果夾角＜80 °，則滿足標準和TCL決議中平面橋接角＜80 °的要求，如果不滿足則需要剔除部分角度對應的路徑。

2.7 分析模型并建立數學模型

對模型中關鍵的橋接角進行簡單的分解（圖8，圖9，圖10，圖11）。

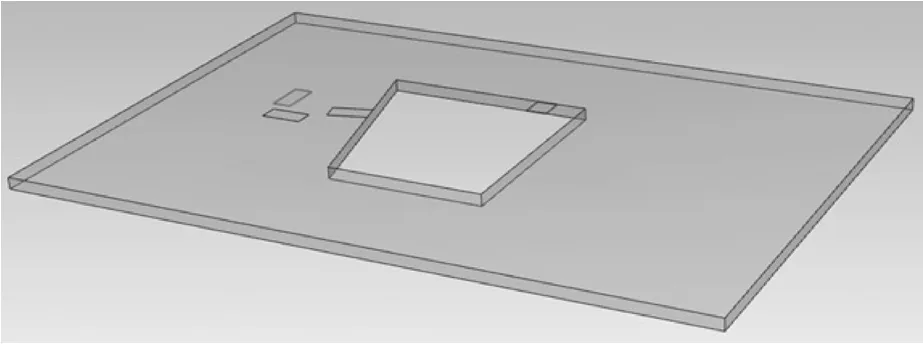
圖4 樣品的三維模型

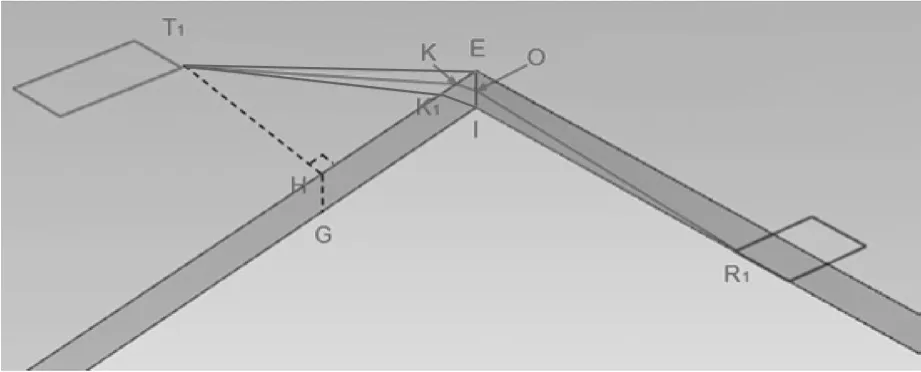
圖5 T1到R1的爬電距離3種可能的路徑模型

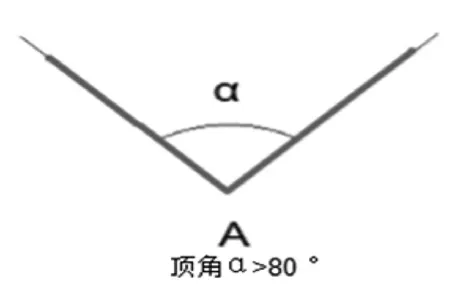
圖6 V型溝槽頂角＞80 °時的爬電路徑

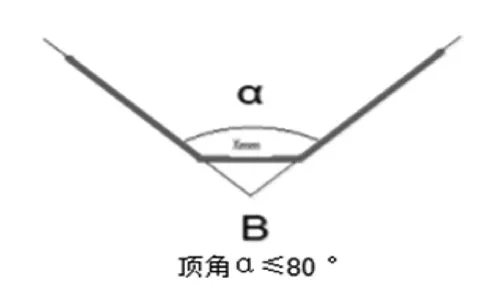
圖7 V型溝槽頂角≤80 °時的爬電路徑

圖 8 樣品橋接角局部實物照片

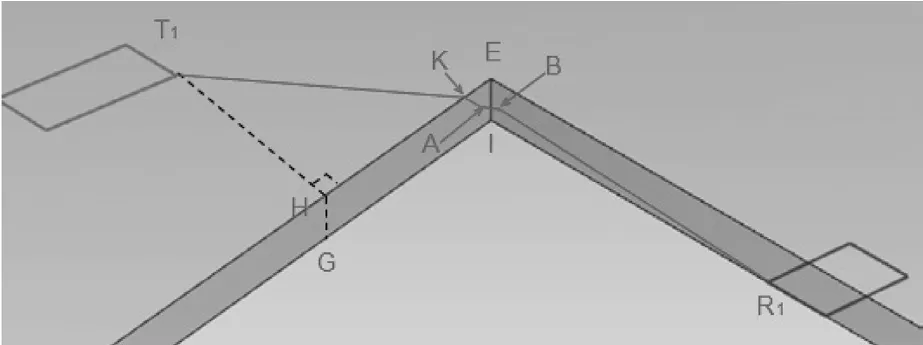
圖9 樣品橋接角局部模型

假設：在橋接的情況下取得爬電距離最小值，T1-KA-B-R1。

對于任意的橋接路線AB必能做出一個（H1-H2-H3-H4輔助平面）垂直于（H3-H4-R1底面）。

對圖10分別沿著H-H1，H1-H3,H2-H4展開得到圖11。

做AB在經過A點且平行于底面（水平平面GIR1）的輔助平面A-F-D。即AD為AB在水平輔助平面A-F-D的投影，A為輔助平面與H1H3的交點，F為輔助平面與EI的交點，D為輔助平面與H2H4的交點。

現在已知：AB=1 mm（2級污染等級X=AB=1.0 mm，3級污染等級X=1.5 mm，1.5 mm的路線有變化后面再討論），T1H，GI，HG，IR1以及θ為定值（可以直接測量得到），求爬電距離最小值T1-K-A-B-R1。

最短路徑可以分段求解T1-K-A-B-R1=T1-K+KA+AB+BR1，AB已知，由展開圖11可知兩點之間線段最短，即T1-K-A為一條直線時取得最短距離T1A。

設AH1為變量（0≤AH1≤HG）；角度∠BAD為變量α，由于要取得最短路徑所以0 °≤α≤90 °；∠FAD為變量β，由三角形內角和為180 °可知：0 °≤β≤180-θ °；∠FDA為γ，γ=180-θ-β。

最短路徑為：

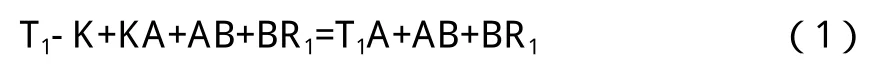
式中：

T1A—為圖11中T1到A的線段路徑；

AB—為圖11中A到B的線段路徑；

BR1—為圖11中B到R1的線段路徑。

由勾股定理可知：

式中：

T1H—為圖11中T1到H的線段路徑；

AH1—為圖11中A到H1的線段路徑；

GH3—為圖11中G到H3的線段路徑；

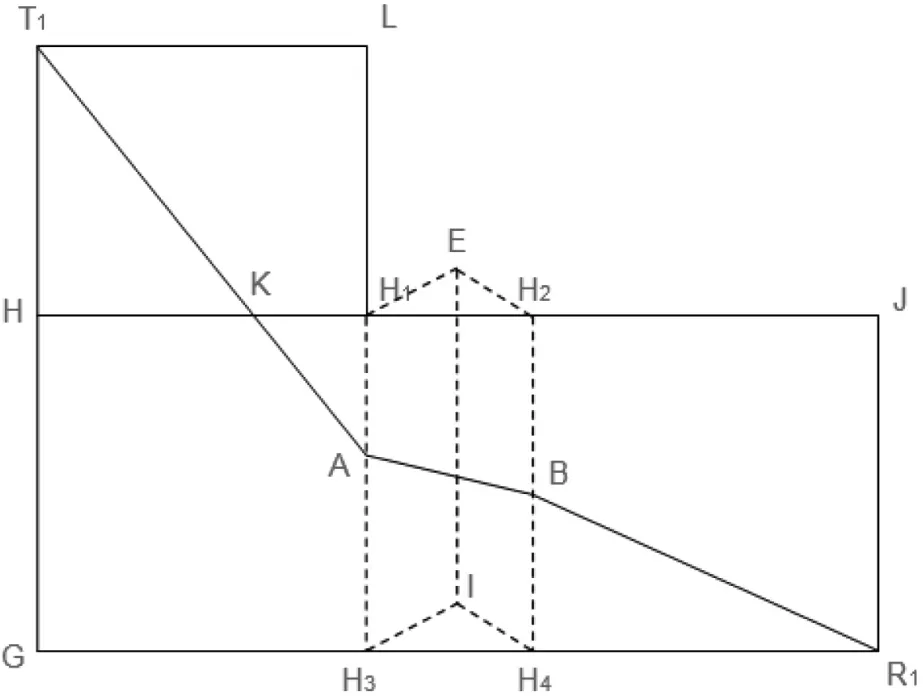
圖11 橋接角展開圖

BH4—為圖11中B到H4的線段路徑；

H4R1—為圖11中H4到R1的線段路徑。

式中：

GI—均為圖10中的G到I線段路徑；

AF—均為圖10中的A到F線段路徑；

HG—均為圖10中的H到G線段路徑；

DB—均為圖10中的D到B線段路徑；

IR1—均為圖10中的I到R1線段路徑

FD—均為圖10中的F到D線段路徑。

又由三角形AFD滿足正弦定理：

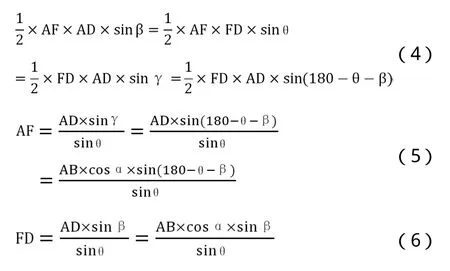
式中：

AD—為圖10中A到D的的線段路徑；

θ，β，γ—均為圖10中的角度。

公式（3）化解為公式（7）

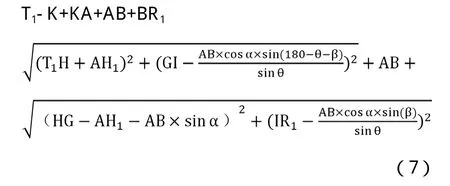
2.8 通過EXCEL輔助計算

在2.7的公式（7）中有3個變量α，β， AH1，通過EXCEL輔助計算。

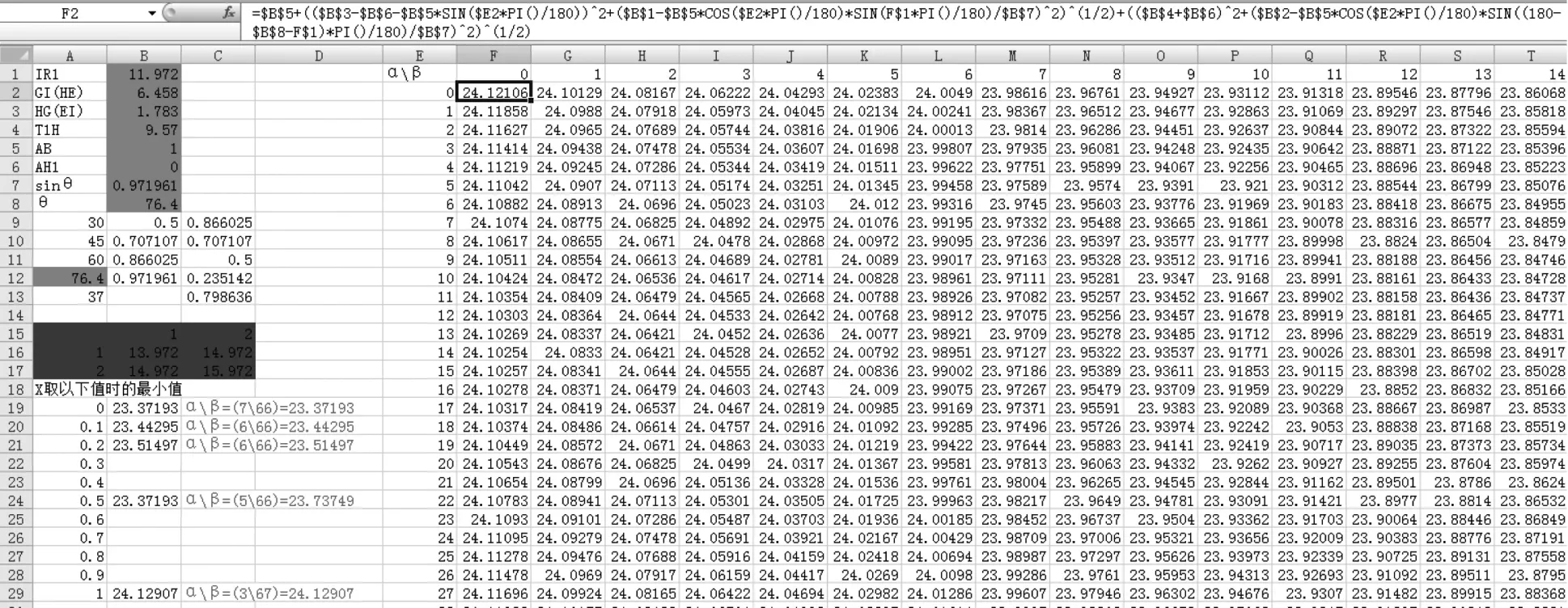
圖12 通過EXCEL計算得到的T1-R1爬電距離最小值

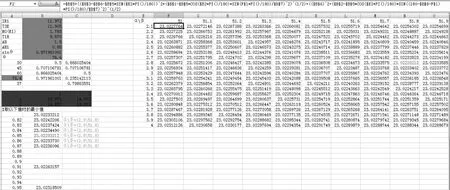
圖13 不同污染等級的T1-R1爬電距離最小值

先取其中α，β兩個角度做表格，找到AH1為定值時，任意角度的爬電距離最小值；又由于已知爬電距離必定存在最小值，再將AH1反復替換從最小取到最大值尋找規律，反復搜索表格中最小值，以及最小值取得的對應角度，得到T1-R1爬電距離最小值如（圖12）在AH1為0，α=7 °，β=66 °時，取得爬電距離最小值為 23.37193≈23.372。

從結果可以看到路徑3是明顯小于路徑1和路徑2的值的。

2.9 計算步長的選取與結果的精確度

此時還應當對角度α，β和AH1尺寸進一步細化，計算步長選取0.1 °和0.01 mm精確度,此時取得最小值AH1為0，α=6.8 °，β=65.5 °時，取得爬電距離最小值為23.371 87≈23.372.從表1中可知：最短爬電距離到小數點后第四位才發生變化，二者數據相差只有0.000 06 mm，基本可以忽略，所以選取1 °和0.1 mm精確度已經足夠滿足要求。

表1 采用不同計算步長求得的最短爬電距離

圖14 計算爬電距離最小值的JAVA代碼

圖15 通過代碼計算得到的爬電距離最小值的結果

2.10 驗證橋接角

最后還需要驗證不橋接所形成的最短路徑夾角是否＜80 °，如果夾角＜80 °，則滿足標準和TCL決議中平面橋接角＜80 °的要求，此處問題又轉化為了求易面直線和線段的最大夾角問題。

由于各個變量在最短路徑的情況下均為已知量，可以建立向量坐標系，聯立方程求解；也可以在模型上不斷的窮舉量取；均可證得此例中最短路徑的情況下，若是不橋接所形成的最短路徑夾角＜80 °（本文中就不再贅述具體證明過程）。

2.11 不同污染等級時的最短爬電距離

當污染等級為3級，AB=1.5 mm時，T1-T2和T2-T3之間路徑分別小于1.5 mm，在爬電距離計算中直接跨接視為0，最短路徑轉化為T3-R1。同理可得最小值，但是最小值并不是在AH1為0時取得，取得最小值時AH1為0.85，α=2.8 °，β=51.8 °時，取得爬電距離最小值如（圖13）為23.022 3≈23.022。

3 通過編程計算

2.7中的公式（7）也可以用編程進行輔助運算，可以更加節省時間，得到更加精確的結果，筆者使用JAVA語言輔助計算，相關環境配置此文不再贅述，具體代碼如圖14。

此代碼由于步長太小，計算量過大，容易引起內存溢出，可以考慮變量分段計算，最后得到：當AH1為0，α=6.8 °，β=65.5 °時，爬電距離最小值的結果（如圖15）=23.1873675670287≈ 23.372。

相比于通過EXCEL計算得到的結果更加精確，快捷。

4 總結

爬電距離與電氣間隙的測量幾乎涉及到所有類別的電氣產品，測試方法和要求也仍在不斷完善當中，但測量方法的核心仍應圍繞路徑本身，但是實際被測產品的多樣性加大了測量難度，所以在遇到需要空間橋接或者類似的復雜電氣間隙爬電距離問題時，引入三維建模，數學建模，利用EXCEL或編程運算是未來求解復雜的爬電距離和電氣間隙最小值的一種值得參考的思路和方案。

同時文中提到的建模、利用EXCEL或簡單編程計算路徑的解決方案，在空間路徑的測量方面有著非常實用的前景，適合一般工程技術人員在日常工作中去處理一些空間路徑的相關問題，本文的介紹希望對廣大讀者有所幫助。