單相流作用下圓柱結構振動響應特性研究

張筱璐， 任彤煜， 王秋波， 齊 巍， 李躍娟

（1.北京工業大學機械工程與應用電子技術學院，北京 100124；2.北京工業大學汽車結構部件先進制造技術教育部工程研究中心，北京 100124；3.中國汽車技術研究中心有限公司，天津 300300）

換熱器是石油、化工、動力等行業中實現熱量傳遞的重要設備，在內部流體作用下，傳熱管會發生流致振動. 當殼程流體的流動方向垂直于傳熱管軸線方向時，傳熱管更易發生彎曲變形和損壞.

目前的試驗和數值模擬研究多針對直圓柱結構在水介質流動激勵下的振動響應特性，一般將來流方向定義為順流向，垂直來流方向定義為橫流向［1-3］. Tolentino 等［4］在水洞中對雷諾數范圍為90～350、質量阻尼系數為0.126、底部固定的直圓柱結構開展流致振動試驗，發現在不同雷諾數范圍內，圓柱體的振動響應由不同的頻率決定. 徐萬海等［5］在雷諾數為800～16 000的范圍內研究直圓柱結構順流向渦激振動響應特性，發現順流向響應頻率一般“鎖定”在固有頻率附近. Williamson、Govardhan和Blevins等［6-8］發現低質量比直圓柱結構橫流向振幅隨雷諾數的增大而不再均勻變化，出現分支現象. 康莊等［9］通過對低質量比直圓柱體進行數值模擬，發現雷諾數范圍的增大對圓柱渦激振動的影響主要體現在順流向與橫流向各分支振幅的增加.Jauvtis、Williamson和Wu等［10-12］對橫流向和順流向自由振動的直圓柱開展試驗，并與只在橫流向自由振動的直圓柱對比，發現兩自由度直圓柱順流向振動會增大其橫流向振幅. 唐國強等［13］在0.15～0.6 m/s的速度范圍內研究了以兩端鉸接方式固定的直圓柱管在均勻流作用下的渦激振動問題，發現順流向的主導頻率為橫流向的2倍，并且橫流向和順流向的振幅隨著流速的增大而緩慢增加. 曹淑剛等［14］對質量比為3.24、兩自由度圓柱體進行數值模擬，發現順流向頻率在較低速度下為橫向頻率的2倍，在較高速度下有兩個值，一個為橫向頻率的2倍，另一個與橫向頻率接近.

換熱器中同樣存在彎圓柱管結構，部分學者也針對其流致振動特性開展了相關研究［15-18］. 其中，劉建清等［17］在流量小于30.5 m3/h的范圍內對彎圓柱管進行流致振動試驗，發現彎圓柱體振動主要集中在其低階固有頻率上. Zhu等［18］在雷諾數165～1129范圍內對質量阻尼比為0.11的彎圓柱管進行渦激振動實驗研究，發現彎圓柱管不同位置處的振動頻率不同，表現出多模態響應且橫流向和順流向的最高模態響應不同.

目前，對直圓柱管和彎圓柱管在相同雷諾數下進行振動響應特性的對比研究較少，本文擬在雷諾數為7500～42 000范圍內針對直圓柱管和彎圓柱管分別開展流致振動試驗，測試其在不同流速下順流向與橫流向的振動響應，并進一步分析漩渦脫落頻率、振幅等與流速的關聯規律，探究兩種圓柱結構在相同雷諾數下振動特性的異同.

1 試驗方法

試驗裝置如圖1所示，主要由離心泵、穩壓器、流量控制閥、渦輪流量計、測試部分和水箱組成，水流量可在50～1500 m3/h范圍內調節. 離心泵揚程為85 m，其轉速通過變頻器控制并在出口處接有穩壓器，用以消除離心泵運行帶來的壓力波動. 測試部分由入口段、入口穩定段、試驗段、出口穩定段以及出口段組成，其中試驗段的入口橫截面積為0.06 m2，在距離試驗段入口500 mm 處為測試對象（直圓柱管或彎圓柱管）的安裝位置. 直圓柱管長度為540 mm，彎圓柱管弧長為540 mm，材料均為結構鋼，質量比為3.94，阻尼比為0.10，外徑為17 mm，管壁厚度為2.5 mm. 在分別進行直圓柱管或彎圓柱管流致振動試驗時，兩種圓柱管結構均采用懸臂梁形式安裝，即一端采用焊接加脹接方式固定于試驗段面板上，另一端自由振動. 試驗采用一個三軸加速度傳感器（Endevco2230EM1）測量流場穩定時直圓柱管或彎圓柱管在順流向和橫流向的振動響應，加速度傳感器下表面距離圓柱管自由端表面20 mm（圖2）. 為防止在數采過程中傳感器的安裝和連接線改變圓柱管模型本身的物理參數以及受到外界的電磁干擾，該加速度傳感器均安裝在圓柱管結構自由端的內壁位置. 同時，為防止其他無關介質進入圓柱管結構內對試驗結果造成影響，用橡膠塞對圓柱管結構的自由端進行密封處理.

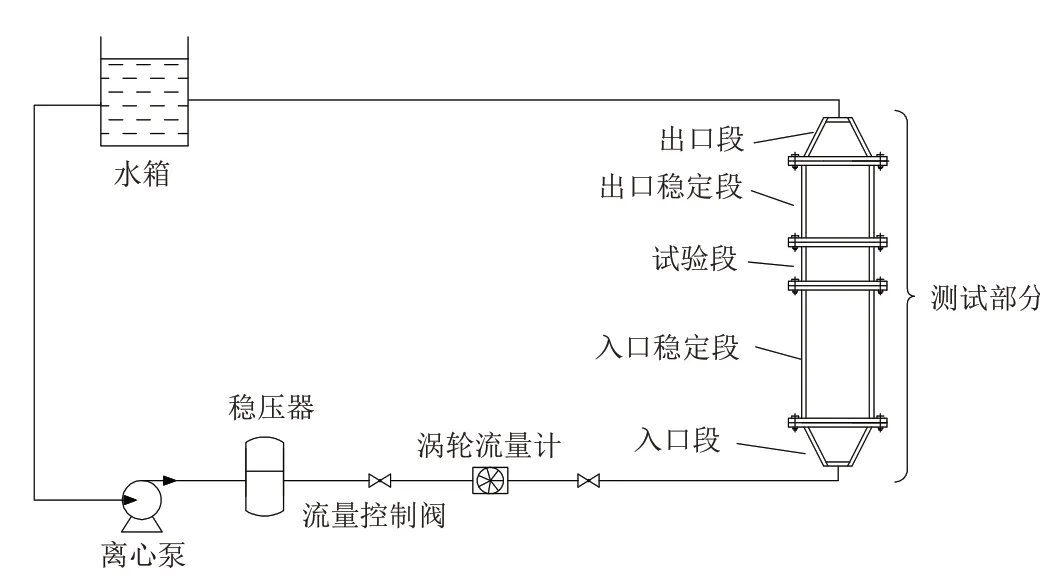
圖1 試驗裝置示意圖Fig.1 Schematic diagram of the experiment equipment

具體試驗步驟為：①試驗開始前啟動離心泵，檢查試驗裝置封閉性并排出試驗裝置中的空氣；②確認系統穩定后，開始以90 m3/h 為初始流量進行流致振動試驗，當渦輪流量計讀數穩定30 s后，開始采集直圓柱管上加速度傳感器數據，時長200 s；③隨后按30 m3/h的間隔流量增加流量，最終達到540 m3/h流量，共對16組流量工況進行測試；④直圓柱管測試結束后，對彎圓柱管重復上述試驗步驟. 試驗數據由LMS Test Lab軟件進行采集處理，得到不同流量下橫流向和順流向的加速度響應. 試驗分析的相關流速和雷諾數由下述公式結合流量及結構參數計算得出.

雷諾數是決定試驗過程中流場特性的無量綱參數，其定義如下：

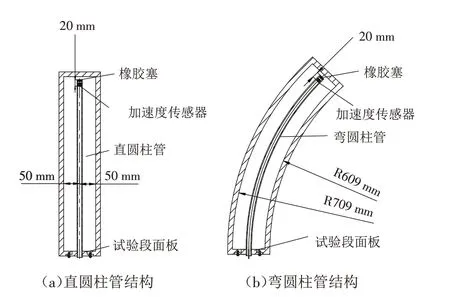
圖2 圓柱管結構加速度傳感器位置示意圖Fig.2 Positions of the accelerometer sensors on the cylindrical tuber structures

式中：ρ 為流體密度；V 為自由流速；D 為圓柱管外徑；μ 為流體的動力學黏性系數；Q 為水流量；A 為試驗段入口自由流通面積.

由公式（1）和公式（2）計算可知，在整個試驗過程中，來流速度范圍為0.45～2.5 m/s，雷諾數范圍為7500～42 000.

在垂直于圓柱管軸線方向的橫向流作用下，圓柱管后會交替出現漩渦脫落，可由斯特羅哈數進行定量描述：

式中：St為斯特羅哈數；fv為漩渦脫落頻率；V 為自由流速；D 為圓柱體外徑.

2 試驗分析與討論

2.1 模態分析

首先采用敲擊模態試驗方法獲取兩種圓柱管結構的前三階固有頻率（表1）. 試驗表明，空氣環境中直圓柱管第一階固有頻率比彎圓柱管略低，且直圓柱管結構和彎圓柱管結構在靜水環境中的固有頻率均小于各自在空氣環境中的各階固有頻率，這是由于圓柱管結構周圍存在的流體耦合作用增加了圓柱管結構自身的等效質量，導致固有頻率降低.

表1 空氣環境與靜水環境中直圓柱管和彎圓柱管的前三階固有頻率Tab.1 Natural frequencies of straight cylindrical tube and curved cylindrical tubes in air environment and still water environment

2.2 流速變化對圓柱結構振幅的影響分析

直圓柱管和彎圓柱管橫流向加速度幅值分別隨流速變化的趨勢如圖3（a）所示，直圓柱管和彎圓柱管橫流向振幅均隨流速的增大而增大. 當流速小于1.91 m/s時，直圓柱管橫流向振幅隨流速的增大而緩慢增大；彎圓柱管在流速范圍為0.45～2.19 m/s時，橫流向振幅也隨流速的增大而緩慢增大，直圓柱管和彎圓柱管在此流速范圍內主要受到湍流抖振的影響［19］. 當流速超過1.91 m/s后，直圓柱管橫流向振幅急劇增大，而彎圓柱管在流速超過2.19 m/s后橫流向振幅急劇增大，這是因為由漩渦脫落誘導的振動逐漸明顯導致的. 結合文獻［6］可知，在雷諾數為7500～42 000時，直圓柱管和彎圓柱管的振幅響應只存在初始分支，初步判斷未發生“鎖頻現象”，此時直圓柱管和彎圓柱管處在2S模態，即在一個振動周期內，圓柱兩側交替脫落一個漩渦.

直圓柱管和彎圓柱管順流向振幅分別隨流速的變化趨勢如圖3（b）所示，直圓柱管和彎圓柱管的順流向振幅均隨流速的增大而先增大、后減小. 這是因為隨著流速的增加，由漩渦脫落誘導的振動逐漸明顯，直圓柱管和彎圓柱管順流向振幅逐漸減小，直圓柱管順流向振幅峰值所對應的流速小于彎圓柱管順流向振幅峰值所對應的流速. 當流速小于1.27 m/s時，直圓柱管和彎圓柱管在相同流速下的順流向振幅接近. 當流速大于1.27 m/s時，彎圓柱管在相同流速下的順流向振幅大于直圓柱管在相同流速下的順流向振幅.

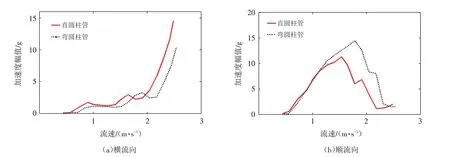
圖3 直圓柱管、彎圓柱管振幅隨流速變化關系Fig.3 Variations of accelerations with flow velocities for the straight cylinder tube and curved cylindrical tube

綜上所述，在流速較高的情況下，直圓柱管和彎圓柱管在相同流速下的振幅不同. 在整個試驗過程中，兩種圓柱管在順流向同時承受流體沖擊力和由漩渦脫落引起的交變應力在順流向的分力. 兩種圓柱管在順流向和橫流向的受力不同導致其在兩個方向的振幅不同. 在相同流速下，直圓柱管橫流向振幅大于彎圓柱管橫流向振幅，這可能是由于彎圓柱管的剛度大于直圓柱管的剛度所致［20］.

2.3 漩渦脫落頻率與流速變化的映射規律

為進一步分析直圓柱管和彎圓柱管橫流向加速度振幅發生變化的原因，圖4 給出直圓柱管、彎圓柱管在四種流速條件下橫流向振動頻譜圖. 隨著流速的增加，兩種圓柱管橫流向頻譜圖里的峰值頻率均增大. 當流速為1.91 m/s 時，直圓柱管和彎圓柱管橫流向的頻譜圖中出現起支配作用的漩渦脫落頻率峰，同時分別在36 Hz 和38 Hz 處存在較小峰值（圖4（a））. 當流速為2.05 m/s 和2.19 m/s 時，直圓柱管的峰值頻率集中在漩渦脫落頻率、固有頻率處；彎圓柱管峰值頻率基本保持不變（圖4（b）、（c））. 這說明與直圓柱管相比，流速的增加對彎圓柱管的振動頻率影響較小. 當流速為2.33 m/s 時，彎圓柱管的振動頻率比直圓柱管的振動頻率高，這是由于漩渦脫落對直管的作用更為明顯（圖4（d））. 通過對比圖4各圖可知，由于漩渦脫落的作用，導致直圓柱管橫流向振幅急劇增大. 直圓柱管和彎圓柱管的振動頻率未在兩種圓柱管的自振頻率附近，未發生“鎖頻現象”.

通過分析不同流速下橫流向振動頻譜圖，得出流速變化對直圓柱管和彎圓柱管結構漩渦脫落頻率的影響規律，如圖5 所示. 對比表1 可知，兩種圓柱管的漩渦脫落頻率未達到各自的固有頻率附近，未發生“鎖頻現象”. 當流速為2.5 m/s時，直圓柱管和彎圓柱管結構的漩渦脫落頻率分別為28 Hz和30.8 Hz（圖4）.直圓柱管和彎圓柱管結構的漩渦脫落頻率最大值之比約為0.9. 由公式（3）可得，直圓柱管和彎圓柱管的斯特羅哈數約為0.2，說明圓柱管幾何形狀對漩渦脫落的快慢程度影響較小，符合圓柱體斯特羅哈數隨流速的變化規律［21］.

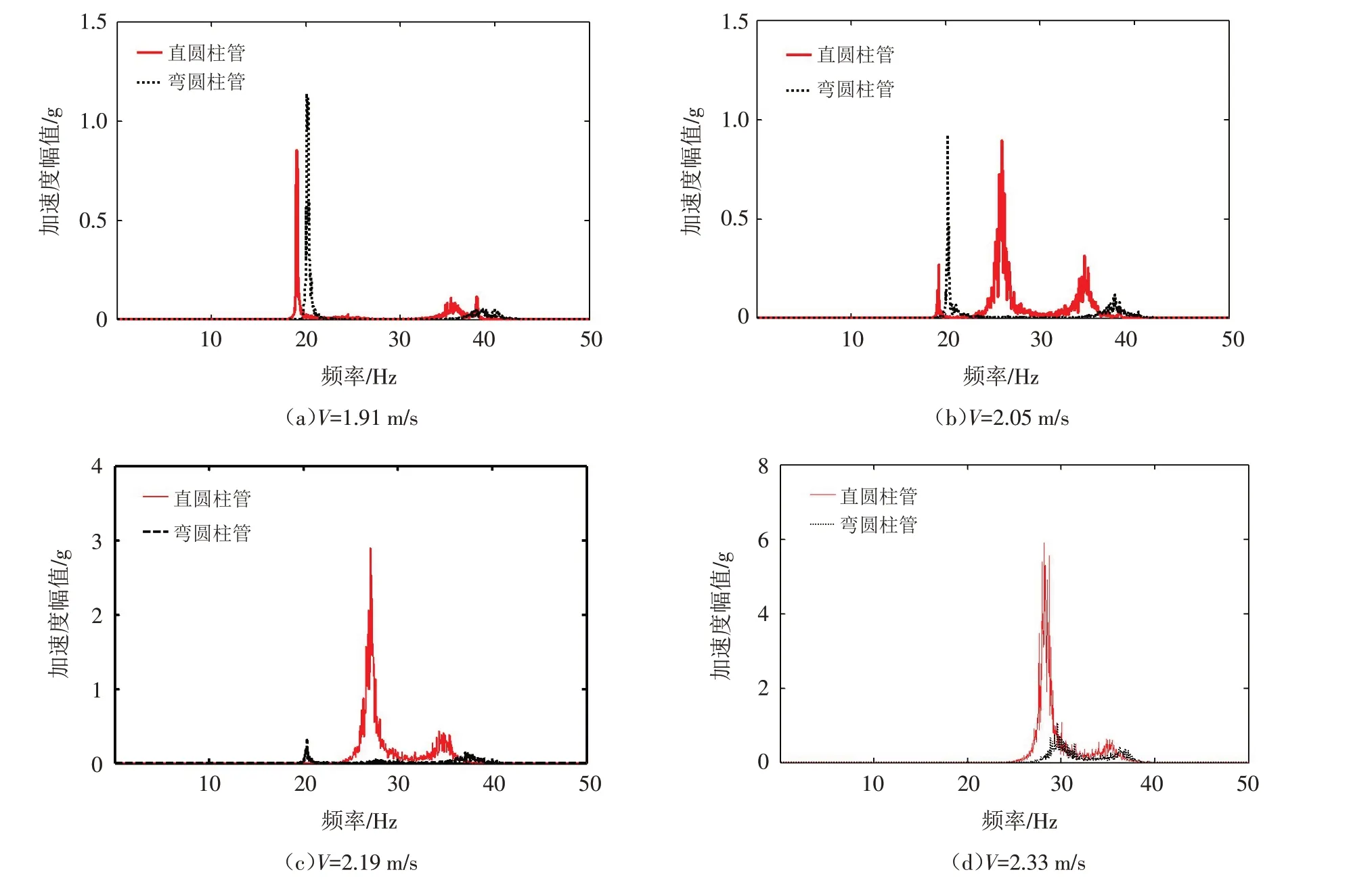
圖4 不同流速下直圓柱管、彎圓柱管橫流向振動頻譜圖Fig.4 Accelerations of the straight and the curved cylindrical tubes with various velocities in cross flow direction

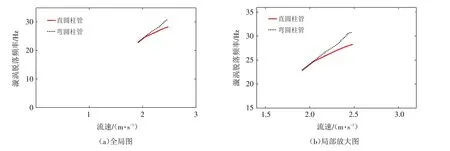
圖5 直圓柱管、彎圓柱管漩渦脫落頻率隨流速變化關系Fig.5 Variations of vortex shedding frequencies with flow velocities for straight and curved cylindrical tubes

2.4 直圓柱管與彎圓柱管順流向振動頻率對比

為分析直圓柱管和彎圓柱管順流向振動頻率的不同，圖6給出兩種圓柱管在四種流速條件下順流向振動頻譜圖. 在試驗過程中，直圓柱管起主要支配作用的峰值頻率約為38 Hz，而彎圓柱管起主要支配作用的峰值頻率約為40 Hz. 由于順流向振動頻率鎖定在固有頻率附近，直圓柱管和彎圓柱管在順流向發生共振，因此當流速為0.45～2.19 m/s，直圓柱管和彎圓柱管順流向振幅大于橫流向振幅. 當流速為2.33 m/s時，直圓柱管在27 Hz處出現局部峰值，與橫流向振動頻率相同. 這說明由漩渦脫落引起的作用力在橫流向分力對圓柱體在橫流向振動產生影響. 對比圖5（a）和圖6（a）可知，當流速為1.91 m/s時，直圓柱管和彎圓柱管順流向主振頻率約是其橫流向主振頻率的2 倍，這符合固定圓柱繞流時順流向振動頻率與橫流向頻率的關系.此時直圓柱管和彎圓柱管的橫向振動近似于簡諧振動，即漩渦在兩種圓柱管后方交替脫落. 對比圖6和表1可知，當流速為1.91 m/s和2.05 m/s時，直圓柱管在順流向發生響應頻率“鎖定”在固有頻率附近的現象，而彎圓柱管在流速為1.91～2.33 m/s時出現該現象.

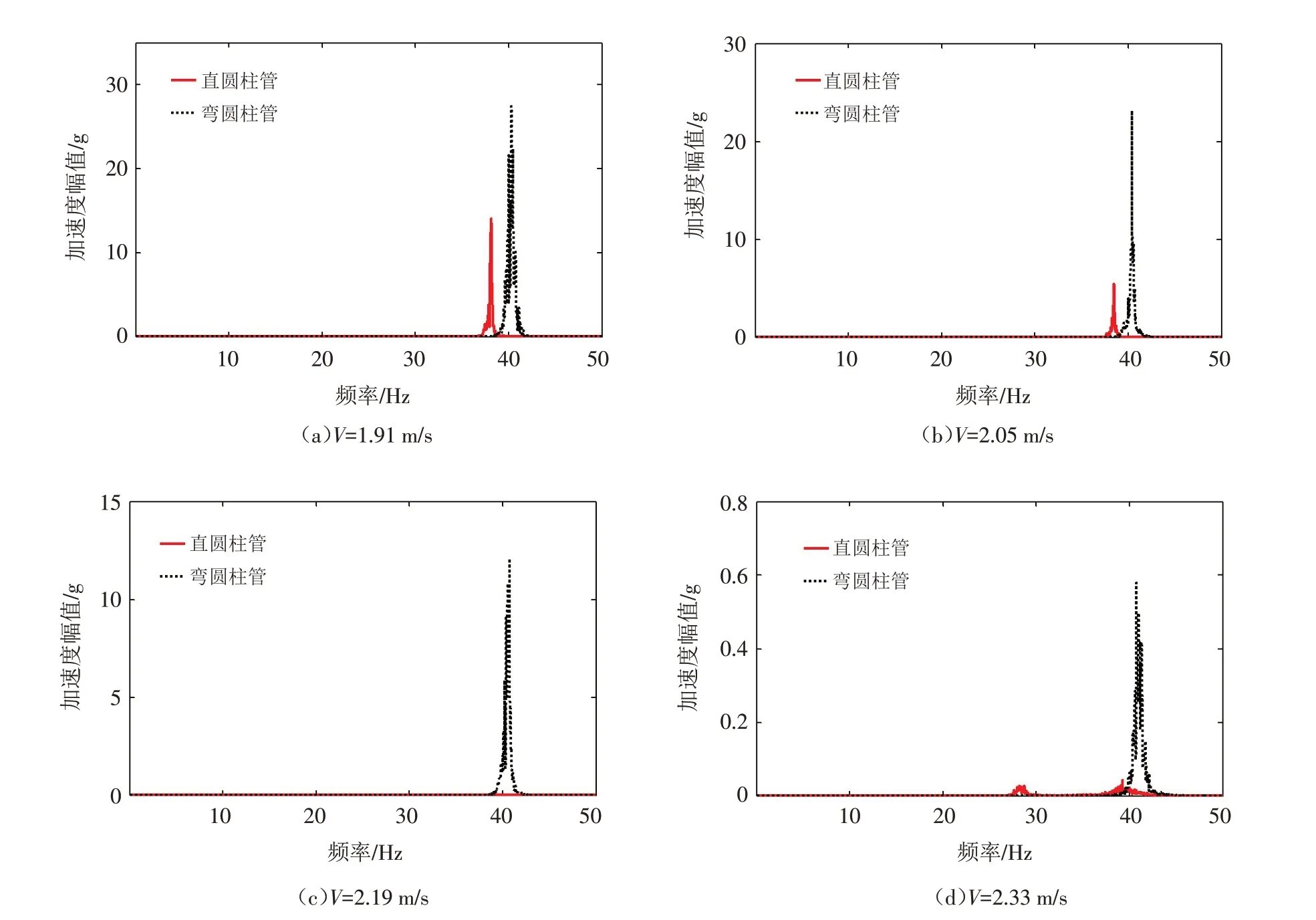
圖6 不同流速下直圓柱管、彎圓柱管順流向振動頻譜圖Fig.6 Accelerations of the straight and curved cylindrical tubes with various velocities in in-line flow direction

3 結論

本文在7500～42 000的雷諾數范圍內分別對直圓柱管和彎圓柱管進行流致振動試驗研究，對比分析發現：

1）直圓柱管和彎圓柱管橫流向振幅均隨流速增大而增大，振幅響應只存在“初始分支”. 在32 000～45 000 的雷諾數范圍內，相同流速條件下的直圓柱管橫流向振幅大于彎圓柱管橫流向振幅，且直圓柱管順流向振幅小于彎圓柱管順流向振幅.

2）直圓柱管和彎圓柱管的漩渦脫落頻率均隨流速的增加而增加，符合固定圓柱繞流變化規律，且相同流速下，彎圓柱管的漩渦脫落頻率比直圓柱管的漩渦脫落頻率高.

3）直圓柱管和彎圓柱管在橫流向均未發生“鎖頻現象”，而順流向的振動頻率“鎖定”在固有頻率附近，且直圓柱管出現該現象的流速范圍（1.91～2.05 m/s）比彎圓柱管的流速范圍（1.91～2.33 m/s）小.