油氣兩相動壓密封自振穩定性流固熱耦合分析*
李雙喜 廖浩然 陳 煉 劉興華 趙 祥
(北京化工大學機電工程學院 北京 100029)
油氣潤滑是指通過壓縮空氣攜帶微量潤滑油進行潤滑的潤滑方式[1],其能夠同時起到冷卻與潤滑的作用。油氣潤滑狀態下的潤滑油始終為液態,對壞境污染小[2],因而廣泛應用于軸承腔、齒輪箱的潤滑。
油氣兩相動壓密封是一種密封介質為油氣混合物的密封裝置,是航空航天等領域高速軸承箱的關鍵元件。密封自振是密封在運行過程中受到干擾并恢復后,補償環在平衡位置發生的后續振動。一般用密封自振穩定性來表征密封發生自振的難易程度,自振穩定性包括軸向和角向的自振穩定性。密封自振穩定性較差時容易引發密封系統失穩,造成嚴重的后果,因此保證密封自振穩定性是密封長久穩定運行的必要條件。
油氣兩相動壓密封作為非接觸密封,具有使用壽命長、維護成本低、泄漏量小的特點[3],且其穩定性以及密封性能優良。現有動壓密封集中于有關槽型的優化[4-5]和溫度場[6-7]的分析。在動態性能研究方面,鄧強國等[8]、張偉政等[9]總結了流體動壓干氣密封研究現狀,提出了微擾法、攝動法、龍格-庫塔法、步進法等多種研究求解方法;李雙喜等[10]求解了動靜壓密封端面間氣膜雷諾方程;GREEN和BARNSBY[11]推導得到了非接觸式氣密封動態穩定性數值分析方法。
在自振穩定性研究方面,劉雨川等[12]提出了角向氣錘自振概念,研究了不同端面結構對密封穩定性的影響;馬綱等人[13]應用簡正模驗證了角向氣錘振動的存在并總結了其對密封的影響;徐萬孚等[14]研究了氣膜密封軸向、角向剛度對自振穩定性的影響,總結了剛度與自振穩定性的關系;張樹強等[15]研究了動靜壓混合式氣體密封的自由振動臨界失穩條件。
現有研究多集中于單相自振穩定性能研究以及油氣兩相流體性質的相關研究,缺少考慮熱與變形下油氣兩相流體密封自振穩定性的研究。本文作者基于前人對油氣潤滑機制、動壓密封性能、自振穩定性的研究,修正氣體雷諾方程,采用流固熱耦合數值分析方法,分析在油氣兩相工況下螺旋槽動壓密封的動態性能,得到油氣比、轉速、壓差和O形圈阻尼等參數對密封自振穩定性的影響。
1 油氣兩相動壓密封結構與工作原理
1.1 密封結構
油氣兩相密封示意圖如圖1所示,密封端面外徑側與軸承相鄰,工作時由噴油嘴噴出兩相潤滑介質潤滑軸承,腔內循環氣體,一般將軸承腔內介質視為分布均勻的油氣兩相潤滑介質。油氣兩相密封組件由動環和靜環組件兩部分組成,動環隨軸旋轉,靜環組件固定在腔體上,動靜環的接觸面稱為密封端面。靜環組件包括靜環、O形圈、彈簧墊、波形彈簧和彈簧座。
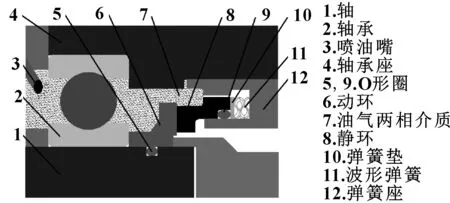
圖1 油氣兩相動壓密封示意Fig 1 Schematic of oil-gas two-phase dynamic pressure sealing
1.2 工作原理
油氣兩相密封靜止時由波形彈簧提供閉合力,將靜環緊緊貼在動環上,起到密封效果。在高速運轉時,油氣兩相流體進入流體動壓槽,產生一層具有一定剛度的流體膜,在推開動靜環的同時密封住油氣兩相介質,達到無摩擦磨損、零泄漏甚至倒吸的效果。其動力學模型如圖2所示。
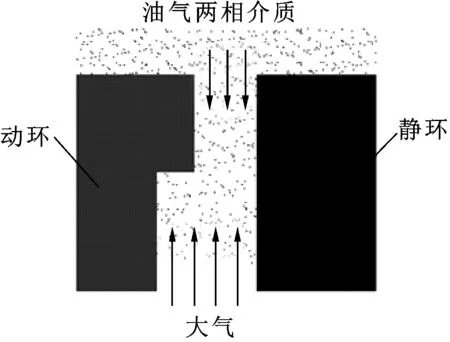
圖2 密封原理Fig 2 Sealing principle
1.3 密封參數
動環端面螺旋槽尺寸對運轉形成流體膜的剛度以及旋轉時流體膜厚度的影響很大。油氣兩相動壓密封端面結構參數包括外徑、內徑、螺旋槽外徑、螺旋角、槽深、槽壩比、槽寬比、槽數端面結構示意圖如圖3所示。

圖3 端面結構示意Fig 3 Schematic of the end face structure
文中針對某軸承箱油氣兩相動壓密封的結構展開分析,端面尺寸[16]如表1所示。潤滑油和空氣的物性參數如表2所示,密封分析參數如表3所示。
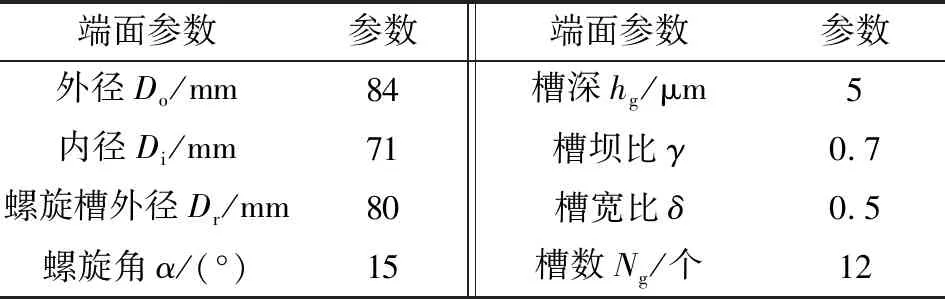
表1 端面結構尺寸

表2 密封介質物理性質

表3 密封分析參數
2 油氣兩相動壓密封自振穩定性數學模型
2.1 動態分析模型
以動環端面中心為原點建立坐標系,油氣兩相動壓密封動力學模型如圖4所示。補償環靜環初始平衡位置為ho處,在密封受到來自外界的擾動時,靜環會沿z軸方向發生軸向振動、繞x軸和y軸發生角向振動,振動方向的密封動靜環旋轉為周期運動,假設圖5中補償環靜環的微擾運動定義為簡諧運動,z(t)、α(t)、β(t) 3個方向運動方程如式(1)所示。經過推導獲得動壓密封18個動態性能的表達式[17],如式(2)所示。
(1)
式中:t為時間;i為虛數單位;ν為補償環受到微擾的頻率。
(2)
式中:kmn、cmn(m,n=z,x,y)代表油氣兩相介質流體膜的動態性能參數;pzr、pαr、pβr、pzi、pαi、pβi參數計算如式(3)所示。
(3)
其中p的計算公式如式(4)所示。
(4)
利用MatLab求解式(2),獲得油氣兩相動壓密封動態性能參數。Δz、Δα和Δβ定義如圖4所示。
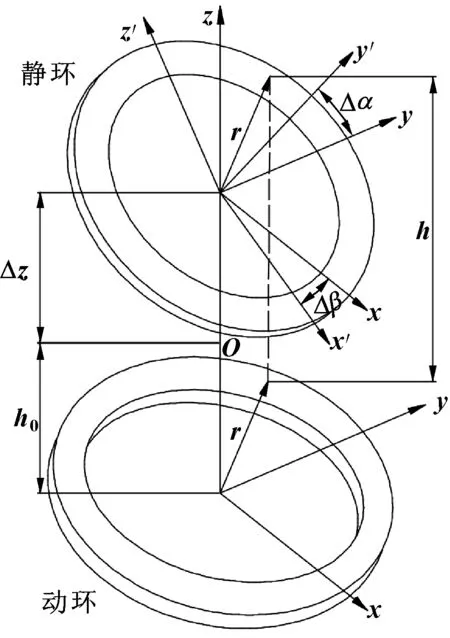
圖4 油氣兩相動壓密封動力學模型Fig 4 Oil-gas two-phase dynamic pressure sealing dynamic model
2.2 自振穩定性分析模型
補償環的振動分為軸向自振和角向自振。軸向可將動壓密封補償環視為一個彈簧-阻尼系統,如圖5所示。當非補償環受到微小擾動,補償環系統將產生自振。
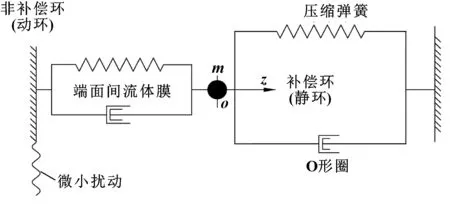
圖5 分析模型示意Fig 5 Schematic of the analysis model
2.2.1 軸向自振運動方程
軸向自振方程表達式為
(5)
令c=(czz+cs),k=(kzz+ks),則有:
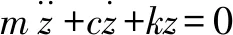
(6)
設ω0為系統固有頻率;δ為阻尼系數;ζ表示阻尼比,有:
(7)
阻尼比ζ<1、ζ=1、ζ>1時振動方程不同,在阻尼比ζ≥ 1的情況下,補償環的運動會逐漸衰減,此時由于阻尼的作用,補償環的自振隨著時間而減小,故在此種情況下,補償環系統不會發生失穩。在阻尼系數ζ<1時,為欠阻尼狀態,其振動方程如式(8)所示。
z=e-δt[C1cos(ωdt)+C2sin(ωdt)]
(8)
在ζ<1時,補償環運動因為阻尼系數δ的取值分為以下3種情況,同時據式(8)可知:
(1)δ<0:此時-δt>0,即補償環的振幅隨著時間t的增加而遞增,最終導致系統失穩。
(2)δ>0:此時-δt<0,即補償環的振幅隨著時間t的增加而減少,最終保持系統穩定。
(3)δ=0:此時-δt=0,即系統振幅變化為三角函數,補償環簡諧振動。
由分析可以看出,在δ=0時為系統長期運行失穩或穩定的臨界判斷點。取此時的系統頻率以及質量為臨界頻率和臨界質量。
設δ=0,此時的振動方程如式(9)所示。
z=eiυcrt
(9)
式中:υcr為密封的臨界頻率。將式(9)代入式(6)得:
(10)
當虛部等于0時計算臨界頻率:
c=czz+cs=0
(11)
實部相等計算臨界質量:
(12)
因此,油氣兩相動壓密封軸向自振穩定性判據為
(13)
式中:υzcr表示軸向臨界轉動頻率。
即在滿足式(13)條件下補償環保持軸向自振穩定。
2.2.2 角向自振運動方程
角向自振運動方程為
(14)
式中:Ix=Iy=I;ksx和ksy為角向剛度,csx和csy為輔助O形圈的角向阻尼,可由式(15)[18]計算得到。
(15)
設α=C1ert,β=C2ert,其中r=λ+iυ。將式(15)代入式(14),當C1、C2存在非零解時:
a0+a1r+a2r2+a3r3+a4r4=0
(16)
式中:
(17)
λ=0時為密封的臨界失穩狀態,則有
r=iυcr
(18)
可得到密封角向自由振動臨界轉動慣量為
(19)
式中:keq為角向自振恢復力矩等效剛度,其計算式為
(20)
因此,油氣兩相動壓密封角向自振穩定性判據為
(21)
式中:υωcr表示角向臨界轉動頻率。
即在滿足式(21)條件下補償環保持角向自振穩定。
2.3 油氣兩相雷諾方程
假設油氣兩相介質中油滴與空氣混合均勻,油滴之間相互獨立,不會相互影響。將密封端面間的流場單元化,其單元物理模型[19]如圖6所示
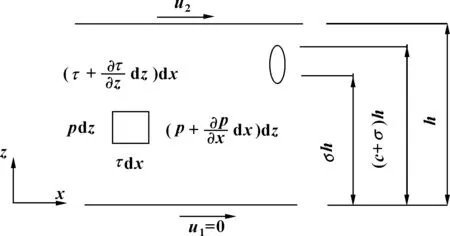
圖6 密封端面間油氣兩相流體的物理模型Fig 6 Physical model of oil-gas two-phase fluid between sealed end faces
油氣比c0即為油滴在兩相介質中所占的體積比,膜厚h為密封端面間流體膜厚。經過推導得到修正黏度μm計算公式如式(22)所示[20]。
(22)
實際情況中黏度隨溫度、壓力變化較小,為了方便計算,假設黏度為常數。
油氣兩相流體的等效密度ρm為
ρm=ρliqco+ρgas(1-c0)
(23)
式中:ρliq、ρgas分別為液體和氣體密度。
綜上得到用于求解油氣兩相密封端面流體膜壓力分布的修正壓力控制方程(Reynolds方程)如公式(24)所示。
(24)
式中:rL、θ分別為所研究流域極坐標中的長度與角度。
通過求解油氣兩相動壓密封穩態方程與流固熱耦合計算,求流體膜端面壓力分布,如圖7所示。

圖7 油氣兩相流體膜壓力分布云圖Fig 7 Oil-gas two-phase fluid membrane pressure distribution contour
再通過求解動態性能的油氣兩相動壓密封非穩態雷諾方程獲得動態性能參數,進而求解臨界頻率、臨界質量、臨界轉動慣量,分析補償環自振穩定性。
2.4 流固熱耦合計算模型
流固熱耦合分為固體域計算、流體域計算、熱計算3部分,在動靜環推開以后,端面形成1~4 μm厚的流體膜。密封端面變形會影響流體膜的厚度以及流體膜的壓力分布,從而影響開啟性能。運行過程中密封受熱產生熱變形,進而影響端面變形以及膜壓。此三者之間相互影響形成一個穩定的狀態,其流固熱耦合流程圖如圖8所示。密封端面的微小變形對摩擦生熱影響不大,此處只考慮溫度對密封環變形的單向影響。具體計算方法如下:

圖8 流固熱耦合分析流程Fig 8 Flow of fluid-solid-thermal coupling analysis
(1)根據實際結構對密封環進行建模并劃分網格,其靜環網格如圖9所示,計算求出密封環的變形矩陣。利用密封環變形分量δij和δid修正流體膜初始厚度,即hi=ho+δij+δid,所得到的hi即為流體域計算初始厚度修正值。
圖9 靜環網格Fig 9 Static ring grid
(2)根據熱計算過程得到密封環在環境溫度和黏性剪切熱下的熱變形δkj和δkd,再一次對膜厚初始值進行修正,即得到流體域計算初始值。
(3)進行流體域部分計算,得到流體膜部分的壓力分布p1,將壓力作為邊界條件重新進行固體域計算,得到密封環的變形δ′ij和δ′id。新的流體膜膜厚為h′i=ho+δ′ij+δ′id+δkj+δkd,將新的流體膜膜厚h′i代入流體域進行計算,設定壓差精度(ε)進行迭代計算。當壓差在精度范圍內,則視為流體膜壓力分布、密封環變形達到穩態,完成流固熱三大部分的耦合。
2.5 計算模型準確性驗證
Λ是壓縮數,其表達式為
(25)
壓縮數對臨界頻率比影響如圖10所示。文中所用油氣兩相動壓密封數學模型計算所得結果與文獻[20]中結果趨勢相似且數值差距較小,驗證了數學模型的正確性。

圖10 臨界頻率計算結果的對比驗證Fig 10 Comparison of calculation results of critical frequency ratio
臨界頻率、臨界質量和臨界轉動慣量是自振穩定性的表征參數,在密封運行過程中油氣比、轉速、壓差和O形圈阻尼等參數的變化可能會引起機械密封自振。分析機械密封運行過程中油氣比、轉速、壓差和O形圈阻尼等參數對臨界頻率和臨界質量的影響,對密封自振穩定性設計有指導性意義。
3 結果及分析
3.1 油氣比對密封自振穩定動態特性的影響
油氣比對密封自振穩定動態特性的影響如圖11所示,圖中耦合前后油氣比對軸向臨界頻率、軸向臨界質量、角向臨界頻率和角向臨界轉動慣量的影響趨勢相同,說明流固熱耦合前后流體進出端面的微流動機制相同。耦合產生的變形對局部流體以及性能產生了影響,導致4個表征參數不同。如圖11(a)所示,油氣比小于0.1前耦合后兩相介質臨界頻率較大,而油氣比大于0.1時相反。這是由于氣相可壓縮性強,對耦合產生的變形敏感進而對軸向臨界頻率的影響較大。
如圖11(a)、(b)所示,軸向臨界頻率隨著油氣比的增加而減小,軸向臨界質量隨著油氣比的增加而增加,在油氣比c0為0.1~0.15時,軸向臨界頻率以及軸向臨界質量相對較大。如圖11(c)、(d)所示,油氣比c0為0.15左右時角向臨界頻率和角向臨界轉動慣量相對較大。綜合考慮油氣比對各表征參數的影響,油氣比c0在0.1~0.15時,油氣兩相動壓密封自振穩定性較好。
3.2 轉速對密封自振穩定動態特性的影響
轉速對密封自振穩定動態特性的影響如圖12所示,耦合前后純氣相以及耦合前后油氣兩相的軸向臨界頻率、軸向臨界質量、角向臨界頻率以及角向臨界轉動慣量在轉速變化下的變化趨勢大致相同。耦合后的純氣相介質以及油氣兩相介質軸向臨界頻率、角向臨界轉動慣量大于未耦合的情況,而軸向臨界質量與角向臨界頻率與耦合后介質的變化規律則相反。這是由于壓力以及溫度的作用使得端面產生一定的發散錐度,使得軸向接觸面積減小,軸向臨界頻率減小;產生的角向阻力減小,角向臨界頻率增加。
如圖12(a)、圖12(b)所示,軸向臨界頻率和軸向臨界質量隨著轉速提升而減小,同時變化速率減小,這是由于轉速增加,螺旋槽產生動壓效果使得開啟力增加,軸向自振穩定性變差。如圖12(c)、圖12(d)所示,角向臨界頻率隨著轉速提升而平穩增加,角向臨界轉動慣量則相反。這是由于轉速增加使得端面間油氣兩相介質分布更加均勻,設計油氣兩相動壓密封中應在實際轉速下綜合考慮4種參數的大小,規避失穩。

圖12 轉速對密封自振穩定動態特性的影響Fig 12 Effect of rotational speed on the self-vibration stability of the seal (a)axial critical frequency;(b)axial critical mass; (c)angular critical frequency;(d)angular critical moment of inertia
3.3 壓差對密封自振穩定動態特性的影響
如圖13(a)所示,壓差增大雖然使得端面間開啟力增加,但在載荷系數較大的情況下,壓差增大使得端面閉合力增加,因此軸向臨界頻率隨著壓差的增加而增大且變化趨勢加大。
如圖13(b)所示,軸向臨界質量在壓差變化的情況下基本保持不變。即在補償環質量小于軸向臨界質量的條件下,壓差增大能夠增大密封軸向自振穩定性。如圖13(c)所示,由于壓差增大使得徑向流體膜壓力分布跨度增大,不利于角向自振穩定性,角向臨界頻率隨著壓差的提升而減小。如圖13(d)所示,臨界轉動慣量隨著轉速的提升而增大。這是由于壓差增加導致軸向閉合力增加,軸向穩定性更好,同時角向條件更加苛刻,容易受到干擾發生失穩。
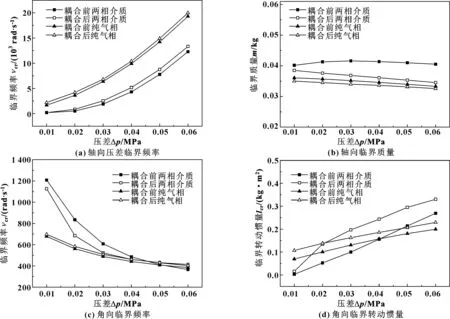
圖13 壓差對密封自振穩定動態特性的影響Fig 13 Effect of differential pressure on the self-vibration stability of the seal (a)axial critical frequency;(b)axial critical mass; (c)angular critical frequency;(d)angular critical moment of inertia
3.4 O形圈阻尼對密封自振穩定動態特性的影響
如圖14(a)所示,軸向臨界頻率隨著O形圈阻尼增加而增大,耦合前后介質情況下計算的軸向臨界頻率差別不大。如圖14(b)所示,O形圈阻尼的變化對臨界質量的大小基本沒有影響。從圖14(c)可以看出,O形圈阻尼的變化對油氣兩相介質角向臨界頻率的影響比純氣相時大。從圖14(d)可以看出,耦合后介質情況下計算的角向臨界轉動慣量,受O形圈阻尼變化影響較大,這是由于端面變形產生的錐度,對臨界轉動慣量計算影響較大。

圖14 O形圈阻尼對密封自振穩定動態特性的影響Fig 14 Effect of O-ring damping on the self-vibration stability of the seal (a)axial critical frequency;(b)axial critical mass; (c)angular critical frequency;(d)angular critical moment of inertia
4 結論
(1)油氣兩相動壓密封軸向臨界頻率隨著油氣比增大而減小,軸向臨界質量隨著油氣比的增大而增大,油氣比在0.1~0.15時油氣兩相動壓密封自振穩定性較好,在補償環質量較大時易選擇大油氣比環境。
(2)轉速較低時軸向自振穩定性較好而角向自振穩定性較差,轉速高時兩者相反,即在極端轉速情況下油氣兩相動壓密封自振穩定性較差。
(3)在滿足臨界質量要求情況下,壓差越大軸向自振穩定性越好,角向自振穩定性較差。壓差達到一定程度后,角向自振穩定性隨壓差增大而不再減小,趨于穩定。低壓差設計時應著重考慮軸向自振穩定性,高壓差則相反。
(4)O形圈阻尼較低時軸向自振穩定性較差而角向自振穩定性較好,O形圈阻尼高時兩者相反,即在取極端O形圈阻尼時,油氣兩相動壓密封自振穩定性較差。由于軸向臨界頻率整體較大,在角向自振穩定性較差時易選用較大阻尼O形圈。

