基于鄰居信息聚合的子圖同構匹配算法

徐周波，李 珍，劉華東，李 萍

（廣西可信軟件重點實驗室（桂林電子科技大學），廣西桂林 541004）

0 引言

圖匹配技術被廣泛地應用于社交網(wǎng)絡、網(wǎng)絡安全、計算生物學和化學等領域［1］中。子圖同構問題是圖匹配問題中的一種，屬于NP 完全問題［2］。研究者們從不同的角度進行研究，致力于提高子圖同構問題的求解效率，并擴大求解規(guī)模。因此，子圖同構問題成為圖匹配問題中研究的熱點。

求解子圖同構問題的方法一般分為3類［3］：基于樹搜索的求解方法、基于索引的求解方法和基于約束滿足問題（Constraint Satisfaction Problem，CSP）的求解方法。Ullmann［4］首次提出了基于回溯的樹搜索算法（以下簡稱Ullmann 算法），該算法基于全局搜索剪枝策略，一一枚舉目標圖與模式圖中的節(jié)點對應的子圖，由于該算法沒有運用剪枝策略來對候選節(jié)點進行過濾，因此隨著圖數(shù)據(jù)量的增加其搜索復雜程度將呈指數(shù)增長。Cordella 等針對已匹配節(jié)點的鄰接點啟發(fā)式信息，給出了VF［5］及VF2［6］算法。VF2 算法基于Ullmann 算法按照節(jié)點度的大小依次選取模式圖節(jié)點，以深度優(yōu)先匹配順序，結合匹配節(jié)點的1步和2步鄰居信息來縮小值域范圍以提高求解效率，是目前主流的子圖同構算法。但VF2 算法并沒有定義匹配順序，針對這一問題，Carletti 等［3］提出了基于VF2 算法的VF3 算法。VF3 算法通過為模式圖的節(jié)點計算選擇概率來決定匹配順序，引入分類概念將節(jié)點進行分類，并在搜索過程中引入向前看策略，更進一步修剪了搜索空間。但正因為引入概率選擇和分類，具有較長的預處理時間。McGregor［2］首次給出了子圖同構問題的基于節(jié)點的CSP 模型，并利用子圖同構的路徑一致性技術，求解子圖同構問題。在此基礎上，Larrosa 等［7］引入相鄰約束，通過同態(tài)傳播來刪除各變量的不可行解。在將圖匹配問題轉(zhuǎn)化為二元CSP 過程中，會造成全局語義的丟失現(xiàn)象，為此Solnon［8］引入了一種全不同約束，通過此約束構建的CSP 模型相較于傳統(tǒng)的CP 的過濾算法，具有更高的求解效率。Audemard 等［9］在Solnon［8］方法的基礎上，增加相鄰變量域的評估值進一步縮小值域范圍?？傮w上，基于CSP 的求解方法，利用圖中的屬性和結構信息，結合傳播約束、弧一致性等技術，迭代地在所有可能的節(jié)點對中過濾掉一定不是解的節(jié)點對，算法的優(yōu)點是求解速度快，但是需要保留不滿足約束的節(jié)點以避免重新搜索，因此對內(nèi)存的需求大?；谒饕那蠼夥椒?，這類方法通常以包含圖的結構和語義信息的向量或特征樹建立索引。Shasha、He 和Zou 等以路徑、樹結構作為過濾特征，給出了GraphGrep［10］、Closure-Tree［11］和Gcod-ing［12］等算法。算法首先查詢模式圖是否存在于目標圖中，并建立相對應的索引，并在最后進行子圖同構檢測。索引信息越豐富，其檢索的效率越高，但隨之而來的問題是需要花費大量的時間來進行索引的建立。

對于如何提高子圖同構的求解效率，現(xiàn)有的研究主要是從兩方面入手：一是優(yōu)化匹配順序［13］，以減少搜索次數(shù)；二是使用更多的鄰居關系來構建約束，過濾不可行的解，以減小搜索空間。對于匹配順序的優(yōu)化，本文通過考慮模式圖和目標圖中的節(jié)點的度和標簽等屬性，計算出匹配節(jié)點的Rank 值，并對Rank 值進行排序，得出優(yōu)化后的匹配順序，以此來為變量序進行賦值。現(xiàn)如今采用鄰居關系來構建的約束，大多數(shù)是基于單個節(jié)點和單個鄰居之間的約束關系，很少有考慮到節(jié)點局部鄰域之間的信息。隨著圖卷積神經(jīng)網(wǎng)絡（Graph Convolutional Network，GCN）［14-15］的出現(xiàn)，可以很好地對圖結構的空間信息進行特征的提取，將節(jié)點的局部鄰域信息轉(zhuǎn)化為節(jié)點的特征向量來進行表示學習。本文通過引入圖卷積神經(jīng)網(wǎng)絡技術對模式圖和目標圖的節(jié)點的結構、屬性特征進行鄰居信息的聚合，使節(jié)點帶有局部鄰域的信息。

本文將采用樹搜索方法并結合CSP求解技術對子圖同構問題進行求解，利用優(yōu)化后的匹配順序?qū)ψ兞啃蜻M行賦值，并將節(jié)點局部鄰域關系轉(zhuǎn)化成約束，來提高子圖同構求解的效率。通過一些公開數(shù)據(jù)集的實驗分析表明，與經(jīng)典的樹搜索算法和約束求解算法相比，本文算法有效地提高了子圖同構的求解效率。

1 相關定義

定義1圖。是一個圖，V是頂點集，E?V×V是邊集，L=是一個標簽集，V中每個節(jié)點都有一個頂點標簽vlabel，且vlabel∈lv。E中的邊都有一個邊標簽elabel，且elabel∈le。

定義2子圖同構。給定目標圖Gt=和模式圖以及映射R?Vt×Vp，若存在單射函數(shù)f：Vp→Vt滿足：

1）?u∈Vp，存在f(u) ∈Vt，使得且lv(u)=lv(f(u))。

2）?u，v∈Vp，u≠v?f(u) ≠f(v)。

3）?(u，v) ∈Ep，存在 (f(u)，f(v)) ∈Et，且le(u，v)=le(f(u)，f(v))。

那么稱Gt的子圖sub(Gt)與Gp是子圖同構關系，記做sub(Gt)?Gp。

子圖同構問題是指在目標圖Gt中找到一個或所有與模式圖Gp同構的子圖。本文的算法是求解所有同構的子圖。定義3CSP。約束滿足問題定義為三元組其中：

1）X={x1，x2，…，xn}為包含n個變量的有限集合；

2）D={D(x1)，D(x2)，…，D(xn)}為n個變量的值域；

3）C={c1，c2，…，cm}為約束集合，約束ci的變量范圍var(ci)={xi1，xi2，…，xij}，且對應的值域val(ci)?Dil×Di2×…×Dij(i=1，2，…，m，1 ≤j≤n)，其中xil∈X(l=1，2，…，j)，Dil為變量xil的值域，稱ci為定義在變量集{xi1，xi2，…，xij}上的j元約束。

CSP 的解指的是對變量集X中的所有變量找到完全實例化，并滿足約束集C中的所有約束。解決CSP 主要有三種算法：回溯搜索、局部搜素和動態(tài)編程，其中回溯算法為應用最廣的算法。

2 基于節(jié)點鄰居信息聚合子圖同構匹配算法

首先，利用圖卷積神經(jīng)網(wǎng)絡技術進行特征表示學習，得出包含節(jié)點局部鄰域信息的特征向量；其次，根據(jù)模式圖與目標圖節(jié)點的標簽、度等屬性對匹配順序進行優(yōu)化；最后，構建子圖同構的CSP求解模型并采用回溯算法對其進行求解。

2.1 鄰居信息聚合

鄰居信息聚合將對圖的節(jié)點進行鄰居信息的聚合，使只有自身屬性特征的節(jié)點帶有局部鄰域信息，并以向量的形式表示出來。文獻［15］所提供的聚合方法主要是針對節(jié)點分類，面對子圖同構問題時，不能將提取的空間特征信息很好地轉(zhuǎn)換為匹配時所需要的權值。鑒于此，本文對文獻［15］的聚合方法進行了改進。

已知模式圖Gp和目標圖Gt，首先，利用模式圖和目標圖的結構屬性特征，分別構建模式圖Gp和目標圖Gt的特征矩陣，并根據(jù)式（1）進行節(jié)點信息的傳播和匯聚：

其中：N(i)為節(jié)點i的所有鄰居節(jié)點集合，deg(i)為節(jié)點i的度，Θ是權重矩陣即機器學習中要更新的參數(shù)矩陣，為節(jié)點i第k次迭代的特征向量。

如圖1所示，圖1（a）為k=1時黑色節(jié)點的鄰居信息聚合示意圖，圖1（b）為k=2 時黑色節(jié)點的鄰居信息聚合示意圖。在圖1（a）中，黑色節(jié)點經(jīng)過圖卷積神經(jīng)網(wǎng)絡，對一步鄰居信息進行匯聚，并得到新的節(jié)點特征向量。與圖1（a）類似，圖1（b）是兩步鄰居信息的聚合。在圖卷積神經(jīng)網(wǎng)絡中是對每個節(jié)點進行聚合。

圖1 不同k值時的鄰居信息聚合示意圖Fig.1 Neighbor information aggregation with different k value

其次，計算節(jié)點的權重值Weight。將得到的節(jié)點的特征向量進行降維操作，并對其取模，即可得到每個節(jié)點的權值。

2.2 優(yōu)化節(jié)點匹配順序

文獻［9］指出節(jié)點的匹配順序的不同會造成查詢次數(shù)的不同，如圖2 所示。針對模式圖p給定兩個匹配順序O1={u1，u2，u3}和O2={u1，u3，u2}，若采用O1的匹配順序與目標圖g1進行匹配時：第1 步將u1與v1進行匹配；第2 步將u2與v2進行匹配；第3步將u3與v2的剩余的鄰居v3進行匹配，發(fā)現(xiàn)標簽不同不是同構子圖，所以只需要匹配3 次就可以知道不是所需要的解。若采用O2的匹配順序，第1 步將u1與v1進行匹配；第2 步將u3與v4進行匹配；第3 步將u2與v4的鏈接的鄰居v5進行匹配，不滿足匹配條件，但v4還有剩余鄰居，則繼續(xù)匹配，發(fā)現(xiàn)直到匹配到節(jié)點v1004還是不滿足匹配條件，針對O2的匹配順序則需要匹配1 003 次才能發(fā)現(xiàn)沒有解；同理，若采用O1的匹配順序與目標圖g2進行匹配需要匹配1 003 次，若采用O2的匹配順序，則只需要匹配3 次。由此可以看出不同的匹配順序?qū)λ阉鞯拇螖?shù)是有很大的影響的。

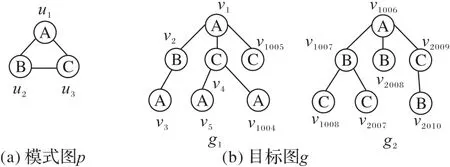
圖2 模式圖p和目標圖gFig.2 Pattern graph p and target graph g

針對此問題，考慮到模式圖中節(jié)點的標簽屬性出現(xiàn)次數(shù)少的應該優(yōu)先匹配，并且節(jié)點的度數(shù)越大，節(jié)點就更具有特殊性。根據(jù)這一特性，給出式（2）對模式圖節(jié)點進行排序，進行匹配順序優(yōu)化：

其中：freq(G，L(u))表示在目標圖G中所有與節(jié)點u標簽一致的節(jié)點總數(shù)量，deg(u)表示節(jié)點u的度。如圖2所示，模式圖p中節(jié)點u1在目標圖g2中的freq(G，L(u1))=1，deg(u1)=2，則Rank(u1)=1/2。計算出模式圖上每個節(jié)點的排序值，按照排序值的大小從小到大對模式圖節(jié)點進行排序。若排序值相同，則隨機排列，由此求出模式圖節(jié)點的匹配順序。

2.3 子圖同構的CSP模型

1）變量集：X=Vp。

2）值域：?xi∈X，D(xi)=Vt。

3）約束集C={c1，c2，c3，c4}：

a）邊約束c1：?xi，xi∈X，xi≠xj

b）節(jié)點標簽約束c2：?xi∈X，若xi=di，di∈D(xi)，則lv(xi)=lv(di)。

c）邊標簽約束c3：Ep，若xi=di，xj=dj，di∈D(xi)，dj∈D(xj)，則∈Et且le(xi，xj)=le(di，dj)。

d）全 不 同alldiff約 束c4：alldiff(x1，x2，…，xn)={(d1，d2，…，dn)|?di∈D(xi)，?i≠j，di≠dj，i=1，2，…，n}。

為了進一步對值域進行縮減，根據(jù)子圖同構問題節(jié)點度的特性，在匹配時要求目標圖Gt中節(jié)點的度數(shù)應當大于或等于模式圖Gp中的節(jié)點，所以可將初始化值域Di更新為：

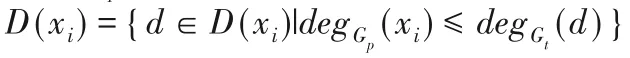
其中：degGp(xi)表示模式圖Gp中節(jié)點xi的度，degGt(d)表示目標圖Gt中與節(jié)點xi的映射節(jié)點的度。

在子圖同構約束求解過程中，有效地構建約束是減小解空間、提高算法的時間效率的重要手段，基于2.1 節(jié)提出的鄰居信息聚合方法，將得到的權重值Weight轉(zhuǎn)化為聚合權值約束，在匹配時提供局部鄰域信息，可進一步地縮減值域，提高算法的效率。進一步，在原約束集中加入鄰域約束NDC，此時將CSP中的約束集更新為C={c1，c2，c3，c4，c5，c6}。

e）聚合權值約束c5：?xi∈X，若xi=di，di∈D(xi)，則Weight(xi)≤Weight(di)。

f）鄰域約束（Neighborhood Dominance Constraint，NDC）［9］c6：?xi，xi∈X，若xi=di，xj=dj，則S(xi，xj)≤S(di，dj) 且(xi，di)∈N(xi)×N(di)，其中N(xi)是模式圖節(jié)點xi的鄰居節(jié)點，S(xi，xj)=MkGp[xi][xj]表示在模式圖中節(jié)點xi到節(jié)點xj步長為k的路徑數(shù)，S(di，dj)=[di][dj]表示在目標圖中節(jié)點di到節(jié)點dj步長為k的路徑數(shù)。

2.4 VFGCN算法

在VF2 搜索算法的基礎上結合2.3 節(jié)給出的CSP 模型，并結合CSP求解技術給出基于圖神經(jīng)網(wǎng)絡技術的子圖同構算法（VF2 algorithm based on Graph Convolutional Network，VFGCN）。算法主要分為4 個步驟：第1 步為各個變量初始值域，根據(jù)度約束和節(jié)點標簽約束對值域進行預處理；第2 步為鄰居信息聚合，利用圖卷積神經(jīng)網(wǎng)絡對節(jié)點進行信息聚合；第3 步為求解匹配順序，為后續(xù)優(yōu)化變量匹配順序做準備；第4步為約束求解，對于不滿足約束條件的解進行回溯。給出偽代碼如下。

算法1 VFGCN。

輸入 模式圖Gp=(Vp，Ep，Lp)和目標圖Gt=(Vt，Et，Lt)；

輸出 所有的子圖同構結果solutions。

算法第1）行函數(shù)Ri根據(jù)模式圖和目標圖節(jié)點的度和節(jié)點的標簽屬性為每個變量返回初始值域，對值域進行預處理，對于不滿足條件的值從各個變量的值域中進行剔除。第2）行函數(shù)Neighbor函數(shù)用于對模式圖和目標圖的節(jié)點進行鄰居信息聚合，根據(jù)式（1）將節(jié)點的局部鄰域信息提取為節(jié)點特征向量并進行降維、取模等操作將向量轉(zhuǎn)化為權值，并返回每個節(jié)點的權值，每個頂點的權值將作為后續(xù)回溯過程的約束條件。第3）行函數(shù)Rank 用于對模式圖節(jié)點的匹配順序進行優(yōu)化，根據(jù)式（2）對模式圖節(jié)點節(jié)點進行計算和排序，返回排序后的模式圖節(jié)點匹配順序S，返回后的順序S即為求解時變量的匹配順序，以優(yōu)化后的順序來為變量進行賦值。算法第4）～15）行為算法的搜索回溯過程，依次從返回的排序的節(jié)點序列S中選取變量，結合CSP 基于回溯的求解方法，若當前的值域滿足Weight權值約束c5、NDC 鄰域約束c6、邊約束c1和邊標簽約束c3，則通過alldiff約束c4更新剩余待匹配變量的值域，保持單射關系，并將該變量從當前變量域中移除。若變量域中的變量并未完全實例化就引起值域的空值化，則說明當前搜索分支無法找到可行解，則算法向上回溯重新進行賦值；若變量完全實例化，即當前變量域為空，且對應的變量賦值滿足所有約束條件，則說明找到一個可行解，并將可行解加入到最終解集中。

3 實驗結果及分析

在Core-i5-6500@3.2 Hz，16 GB 內(nèi)存的實驗環(huán)境下，操作系統(tǒng)是Windows 10，64 位，編譯環(huán)境是pycharm，編譯語言是python。實驗使用了公開數(shù)據(jù)集AIDS（http：//jenalib.leibnizfli.de）和PDBSV2（http：//www.rcsb.org）兩個數(shù)據(jù)集，其中AIDS 為抗艾滋病毒數(shù)據(jù)集，包含大量的稀疏無向圖，節(jié)點數(shù)量從4 到245 不等，每個圖表示化合物的拓撲結構，并包含節(jié)點標簽和邊標簽。目標圖數(shù)據(jù)集中含有10 000幅圖。模式圖按邊的數(shù)量分為Q4、Q8、Q12、Q16、Q20、Q24 六組，每組包含1 000 幅小圖。PDBSV2 數(shù)據(jù)集為蛋白質(zhì)骨架數(shù)據(jù)集，該數(shù)據(jù)集包含40 種蛋白質(zhì)，為中等稀疏圖，節(jié)點數(shù)量從4 000 到12 000 不等。目標圖為40 幅大圖，模式圖按邊的數(shù)量分為Q4、Q8、Q16、Q32、Q64、Q128六組，每組包含40幅小圖。模式圖均為按照邊數(shù)從相應的目標圖中隨機抽取。實驗過程中將使用本文算法與VF2 算法［6］、迭代標記過濾（Iterative Labeling Filtering，ILF）算法［16］、基于路徑的局部全不同（Path of Local All Different，PathLAD）算法［17］、VF3 算法［3］相比較。實驗結果中的平均時間通過式（3）計算得出：

其中：timeall為各個分組求解的總時間，Numpattern為每個分組中模式圖的數(shù)量。平均時間更能體現(xiàn)求解單個模式圖與所有目標圖的子圖同構全部解的時間效率，并統(tǒng)計出兩個數(shù)據(jù)集進行鄰居信息聚合時所花費的時間，計算公式與式（3）一致，timeall為模式圖各個分組或目標圖聚合總時間，Numpattern為各個分組中模式圖的數(shù)量或目標圖的數(shù)量。

基于上述所述，本文算法利用圖卷積神經(jīng)網(wǎng)絡，對模式圖和目標圖節(jié)點的鄰域特征信息進行了提取，并對匹配順序進行了優(yōu)化，減少了搜索次數(shù)，結合CSP 求解技術，提高了子圖同構問題的求解效率。

1）首先在AIDS數(shù)據(jù)集上進行對比實驗，按照模式圖的規(guī)模將實驗分為6 組。實驗結果如表1 所示，由表1 中的數(shù)據(jù)可知在6 組實驗中，VFGCN 算法均優(yōu)于VF2 算法、PathLAD 算法、ILF算法和VF3算法；并且隨著模式圖規(guī)模的增大，求解的平均時間總體呈上升趨勢。由此可以看出，模式圖的大小對于求解時間的影響；但當模式圖規(guī)模為Q24 時，時間卻不是6組中最慢的，但解的個數(shù)是6 組中最少的。原因在于：在搜索的過程中，已提前對不可行的解進行了剪枝，避免了對無效的分支進行搜索，所以盡管模式圖的規(guī)模是最大的，但是時間并非最慢的，因此模式圖的規(guī)模大小對求解時間還是有很大的影響。

AIDS 數(shù)據(jù)集的鄰居信息聚合時間如表2 所示，對于不同規(guī)模的下的模式圖和目標圖，聚合的時間大約都在0.001 4 s左右，由此可以看出聚合步驟所消耗的時間是非常少的，并且不受模式圖規(guī)模的影響。因為不需要重復遍歷圖的所有節(jié)點，只需要遍歷節(jié)點的有限鄰居，所以能夠在極短的時間內(nèi)有對節(jié)點的局部鄰域信息進行聚合，并給出其特征向量，并且在聚合時所選的k值（k步鄰居）影響著后續(xù)的求解效率，在實驗過程中發(fā)現(xiàn)，并不是聚合的鄰居信息越多，即k取值越大，求解效率就越高；反而當k的取值超過一定范圍，將降低求解效率。其原因在于，當k取值過大時，會使得聚合后的特征向量趨于一致，即所有節(jié)點的鄰域信息過于相似，導致在后續(xù)的匹配過程中不能夠很好地對不可行的解進行剪枝，反而影響了求解的效率。經(jīng)實驗測試，對AIDS 和PDBSV2 數(shù)據(jù)集來說，由于模式圖的最大規(guī)模分別為Q24 和Q128，節(jié)點的鄰居大多數(shù)是在3 步之內(nèi)，所以將k取1 時效率是最高的，因此在后續(xù)的實驗過程中k取值為1。

2）本組將在PDBSV2 數(shù)據(jù)集上進行對比實驗，實驗將按照模式圖的規(guī)模分為6組。其鄰居信息聚合時間如表2所示，對比表2 兩個數(shù)據(jù)集聚合的平均時間可以看出，在不同的規(guī)模下，PDBSV2數(shù)據(jù)集的平均聚合時間均比AIDS數(shù)據(jù)集要長，其原因在于節(jié)點的鄰居個數(shù)。PDBSV2 數(shù)據(jù)集整體的圖密度要比AIDS 數(shù)據(jù)集要高，就是相對于AIDS 數(shù)據(jù)集，PDBSV2 數(shù)據(jù)集中的一個節(jié)點可能擁有著更多的鄰居，因此在聚合過程中將花費更多的時間。

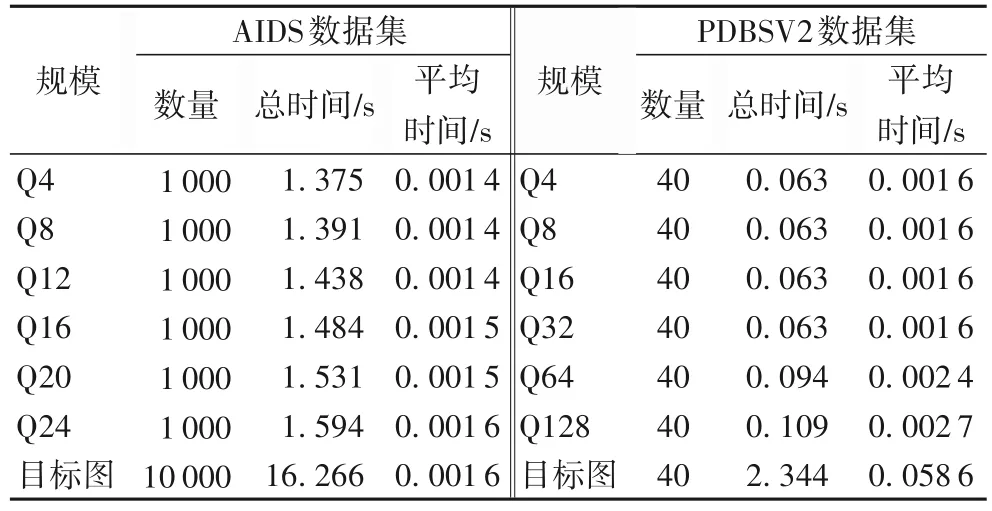
表2 鄰居信息聚合時間Tab.2 Neighbor information aggregation time

與其他算法的對比實驗結果如表3 所示。從表3 中的數(shù)據(jù)可以看出，隨著模式圖規(guī)模的增大，求解的平均時間總體呈上升趨勢。VFGCN 算法求解的平均時間對比VF2 算法、ILF 算法和PathLAD 算法在6 組實驗中均是最短的，對比VF3 算法在規(guī)模為Q64 和Q128 時VF3 算法略有優(yōu)勢。其原因在于，VFGCN 算法對節(jié)點的匹配順序進行了優(yōu)化，降低了搜索次數(shù)，并提取了節(jié)點的局部鄰域信息，對于不可行解更有效地進行了剪枝。但是在規(guī)模為Q64 和Q128 時，VF3 算法首先對模式圖中的節(jié)點計算匹配概率以此來確定匹配順序，并對節(jié)點進行分類，不屬于同一個類別的節(jié)點不能夠進行匹配，在面對規(guī)模更大模式圖的時候比VFGCN 算法更能對值域進行修剪。但是同樣，VF3 算法在計算規(guī)模偏大的模式圖節(jié)點的選擇概率和對節(jié)點進行分類時，所耗費的預處理時間也更長了。

表3 PDBSV2數(shù)據(jù)集上的實驗結果Tab.3 Experimental results on PDBSV2 dataset

4 結語

為了進一步提高子圖同構問題的求解效率，本文提出了一種基于鄰居信息聚合的子圖同構匹配算法，能夠有效地縮減值域。該算法結合圖卷積神經(jīng)網(wǎng)絡技術，利用改進后的聚合公式，對模式圖和目標圖的節(jié)點進行局部鄰域信息的提取及聚合，并且基于圖的標簽、度等特征提供了一種優(yōu)化后的匹配順序，建立子圖同構的CSP 求解模型并進行回溯求解。實驗結果表明，該算法與經(jīng)典算法相比較，有效地減少了子圖同構的求解時間，在小規(guī)模以及中等規(guī)模的圖匹配中有較高的求解效率。在未來的工作中，將研究動態(tài)圖匹配算法，并結合CSP技術中的動態(tài)CSP求解技術對其進行求解。