基于CEEMD 的沖擊回波分析方法研究

朱先祥 ， 許軍才 ， 倪福海 ， 丁 偉

（1.無損檢測技術教育部重點實驗室（南昌航空大學），南昌 330063；2.河海大學 力學與材料學院，南京 210098；3.安徽中盛建設工程試驗檢測有限公司，合肥 230051）

0 引言

沖擊回波法是混凝土結構質量檢測中一種常見無損檢測方法。該方法是根據縱波在結構中的傳播特性對結構質量進行檢測，其原理如圖1 所示[1-2]。利用鋼錘敲擊待測結構表面，沖擊產生的振動波在結構內部傳播過程中，當遇到一定尺度的缺陷或邊界，因2 種材料的波阻抗不同而發生反射和透射現象，結構沖擊表面上的質點就會產生振動響應，這種振動響應以加速度的信號形式被傳感器采集到，再通過對該信號進行快速傅里葉變換（Fast Fourier Transform，FFT），得到反映結構信息的頻譜圖，最后對頻譜圖分析來判斷結構的內部質量情況。

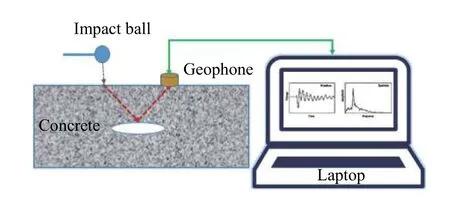
圖1 沖擊回波法基本原理Fig.1 Principle of impact echo method

但是，在實際的檢測過程中很難得到理想的縱波反射信號，通常伴有干擾信號如面波干擾、隨機噪聲以及體波散射等[3-4]。為了解決這一問題，學者提出了不同時頻分析方法，如短時傅立葉變換、連續小波變換及Hilbert-Huang 變換（HHT），來對沖擊回波信號進行分析和研究[5-7]。這些分析方法中，HHT 相對于短時傅立葉變換和連續小波變換能獲取更高的頻率分辨率。集成經驗模態分解（Ensemble Empirical Mode Decomposition，EEMD）是HHT 過程中的關鍵步驟。但是，EEMD 通過加入高斯白噪聲消除模態混疊問題，卻帶來了殘余噪聲的影響，導致分解出的IMF 不是唯一，而加總平均又增大了相應的計算成本[8-11]。為消除EEMD方法的局限性，Torres 提出了一種對噪聲有自適應分解特性的完備集成經驗模態分解（Complementary Ensemble Empirical Mode Decomposition，CEEMD），該方法效果明顯好于早期的EEMD方法[12-13]。

針對傳統方法對沖擊回波信號分析的局限性，本研究將CEEMD 引入沖擊回波信號分析，建立基于CEEMD 的沖擊回波分析方法，通過仿真與試驗證明研究CEEMD 對沖擊回波信號分解后頻譜特征和有效信號提取性能，為實際的沖擊回波檢測方法提供工程參考。

1 方法原理

1.1 沖擊回波原理

沖擊回波法對混凝土結構缺陷處反射信號的有無及強弱來識別缺陷的存在，入射彈性波的反射率越高檢測的分辨率就越高。

根據彈性波傳播理論，彈性波在遇到不同介質的交界面時，會發生反射和折射現象。對于雙層介質，當彈性波從介質1 傳播到介質2 時，其反射率 R計算式為：

式中： z1、 z2分別為介質1、介質2 的波阻抗，對于彈性波而言， z =ρv（ ρ為 介質密度， ν為波速）。

對于夾層介質的情況，如圖2 所示，反射率計算式為：

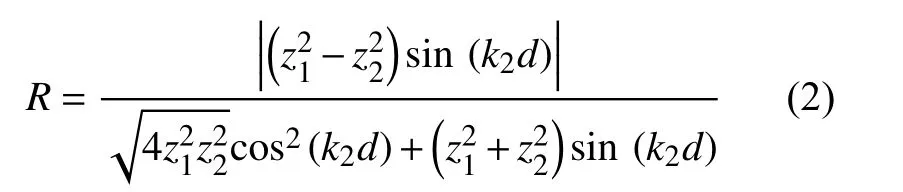
式中： k2為 介質2 中的波數， f 為頻率， d為中間層厚度。

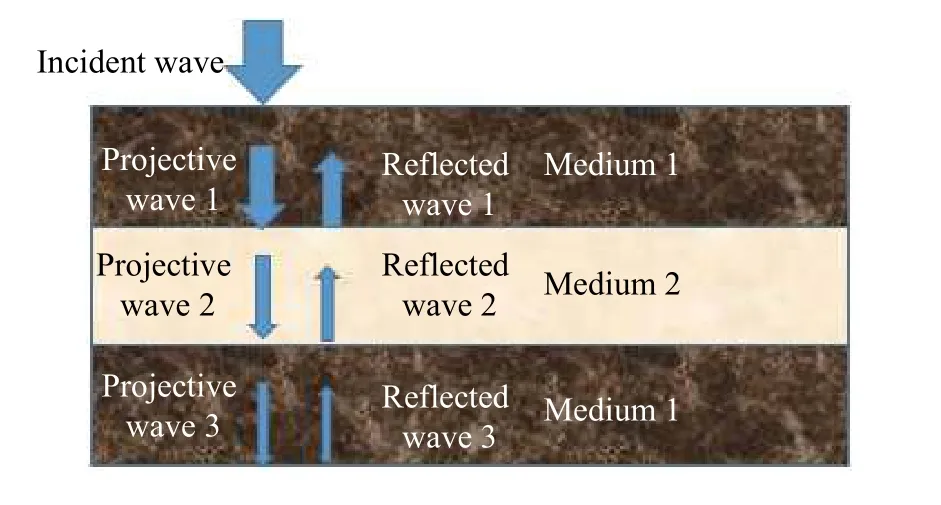
圖2 介質含夾層時彈性波的傳播與反射Fig.2 Elastic wave propagation and reflection in the medium sandwich

沖擊回波測試結構厚度是通過回波信號最大峰值的頻率來計算的，混凝土結構底板厚度或缺陷位置有下列關系式：

式中：D 為底板厚度或缺陷位置，Vp為縱波波速，f 為最大峰值頻率，β=0.96 為經驗校正系數。

1.2 沖擊回波CEEMD 方法

CEEMD 方法在EEMD 的基礎上進行改進，是一種自適應信號分解方法，有效地解決了EMD方法存在的分解不穩定、模式混疊和端點效應等問題。CEEMD 方法基本原理利用添加一對振幅相同、相位相反的高斯噪聲來降低噪聲殘余，方法實現流程（圖3）如下：

首先，將振幅相等、相位相反的n 組輔助高斯噪聲加入原始沖擊回波信號中，從而產生2 個集合IMF：

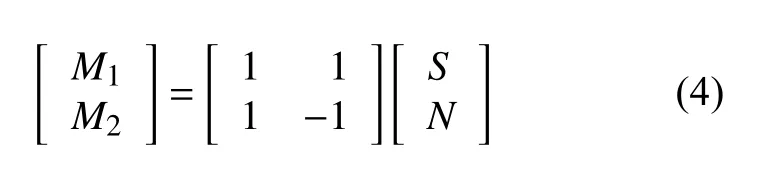
式中：S 代表原始信號，N 為高斯噪聲，M1、M2加入噪聲后的正負對信號集合。

其次，對集合 M1和 M2中所有信號進行EMD分解處理，分解后得到2 組集成的IMF 分量，即IMF1 和IMF2，IMF1 為正噪聲組集成的平均結果，IMF2 為負噪聲組集成的平均結果。

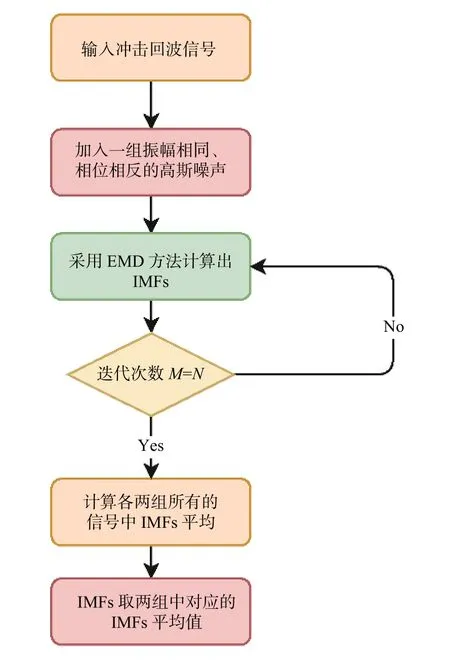
圖3 CEEMD 方法沖擊回波信號分解流程圖Fig.3 Decomposition flow chart of CEEMD

最后，算法分解為2 組IMF 分量，對IMF1、IMF2 集成平均，結果為：

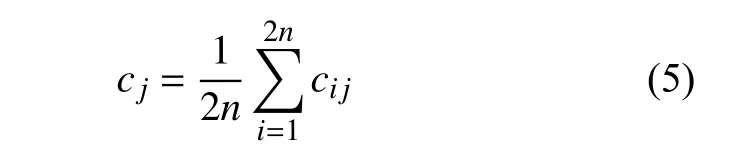
式中：cj代表CEEMD 分離得到的第j 個IMF 分量，cij為i 信號分離所得的編號為j 的IMF 分量。

CEEMD 方法通過在沖擊回波原信號中加入正負對白噪聲，消除了后期進行信號重構時出現的殘余輔助噪聲，不僅繼承了EEMD 方法的優點同時提高了計算效率，而且減小了添加輔助白噪聲帶來的重構誤差[14]。

2 沖擊回波檢測信號分析

2.1 沖擊回波模擬信號分析

設計的仿真模型尺寸為200 mm×200 mm×20 mm 的混凝土板，在板內部有一尺寸為30 mm×30 mm×16 mm 夾層空隙(圖4a)。模擬中計算參數混凝土密度為2500 kg/m3，彈性模量為37.8 GPa，泊松比為0.2[15]。相應的夾層和底部的回波的頻率分別為12.3、9.8 kHz。利用有限元方法對該混凝土板沖擊回波檢測模擬，模擬出的沖擊回波信號如圖4b 所示。

根據圖4 中的沖擊回波信號，利用本研究提出的CEMMD 方法對沖擊回波信號進行分析，將原始信號分解為相應的IMF，原信號分解后的結果見圖5。

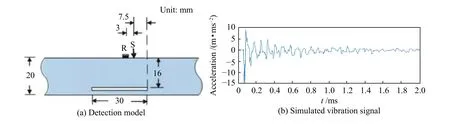
圖4 沖擊回波模擬試驗Fig.4 Impact echo simulation testing

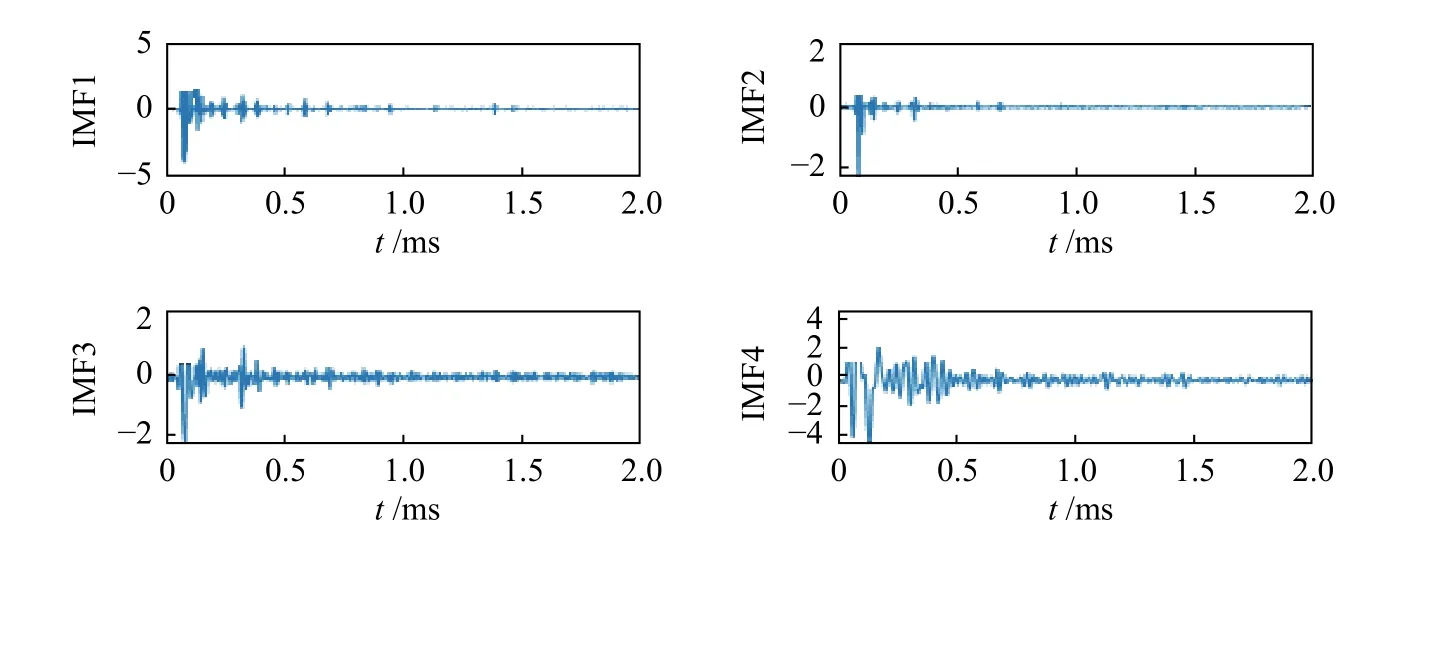
圖5 CEEMD 分解沖擊回波模擬信號的IMFFig.5 IMF decomposed on impact echo simulation signal by CEEMD

根據圖5 結果，CEEMD 方法能夠將原始沖擊信號分解為不同的IMF，模態函數IMF1～IM10。從IMF1～IMF10 特征來看，模態函數振動頻率排序逐漸減小，其中，IMF1～IMF4 主要以高頻為主的成份，IMF5～IMF10 反映了沖擊回波信號結構振動特征，IMF1～IM10 頻率特征如圖6 所示。

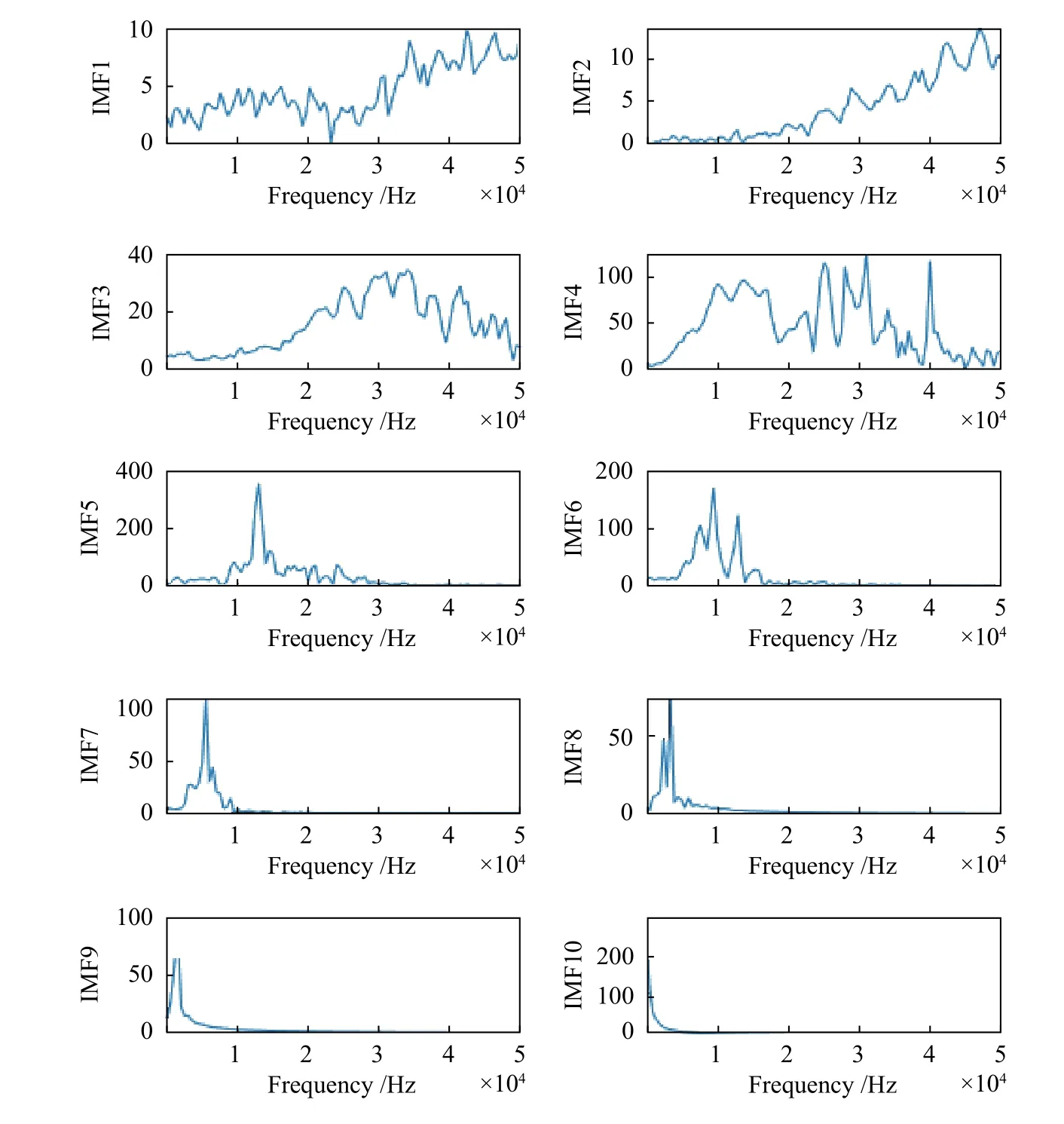
圖6 沖擊回波模擬信號的IMF1～IMF10 頻譜圖Fig.6 IMF1～IMF10 spectrogram on impact echo simulation

圖6 的結果顯示，IMF 能夠很好與沖擊回波信號特征相吻合。IMF1～IMF4 主要體現的是振動沖擊回波信號高頻成份。而IMF5、IMF6 對應的峰值頻率分別為12.3、9.8 kHz，該頻率是來自夾層空隙和板底反射信號的頻率；由此可見，CEEMD方法能夠很好地將板底和夾層空隙處的缺陷很好分離出來，并能對缺陷位置進行確定。

2.2 沖擊回波工程檢測信號分析

以美國弗吉尼亞州Gainesville 15 號公路的沖擊回波現場測試為例（圖7a），現場檢測過程中檢測位置進行了鉆孔取芯，芯樣如圖7b 所示[15]。芯樣路面面層厚度為21.6 cm，面層縱波波速大約為4000 m/s，由厚度和頻率的關系式(3)，計算得到底部反射波頻率為9 kHz。但由于面波和噪聲干擾，圖7a 中的檢測信號的頻譜很難識別出底面的反射波頻率。

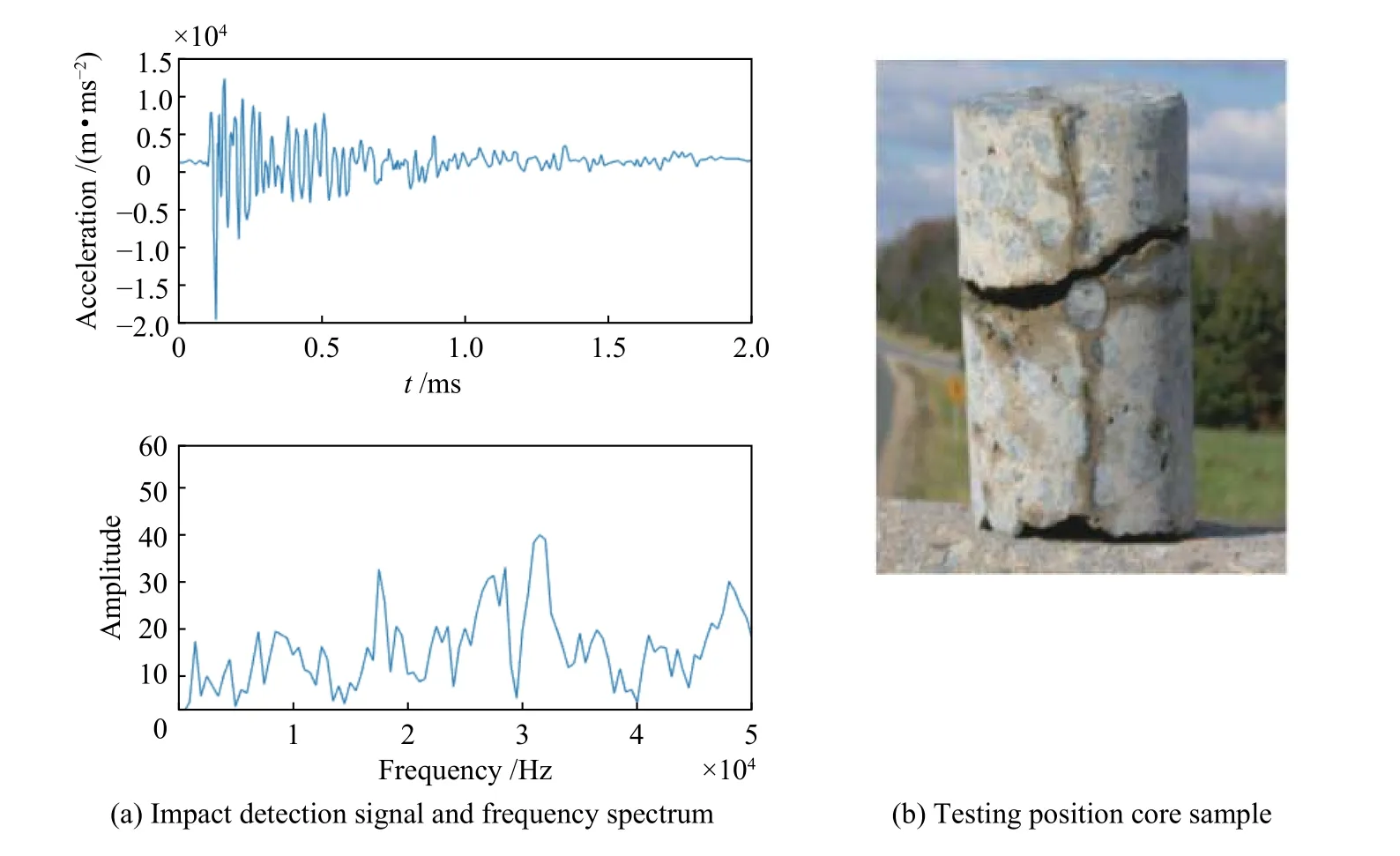
圖7 沖擊回波現場試驗Fig.7 Impact echo on site testing

對該現場檢測的沖擊回波信號采用CEEMD方法進行分析，將該檢測信號分解為相應的IMF，原始信號分解后的結果見圖8。

根據圖8 結果，CEEMD 方法能夠將原始沖擊信號分解為IMF1～IM10 特征模態函數。從IMF1～IMF10 特征來看，模態函數振動頻率排序逐漸減小，其中IMF1～IMF4 主要以高頻為主的成份，主由噪聲信號和干擾信號組成。IMF5～IMF10 反映了沖擊回波信號結構振動特征，IMF7～IMF10 成分為單調函數為主，與上節仿真沖擊回波信號的分析結果一致。對IMF1～IM10 特征模態函數進行頻譜變換，其頻率特征如圖9 所示。

圖9 顯示出IMF1～IM10 特征模態函數變化規律，IMF1～IMF4 主要體現的是振動沖擊回波信號高頻成份，是由噪聲和面波干擾形成的高寬頻信號。而IMF5、IMF6 對應的峰值頻率分別為17.5、9.0 kHz，可判斷出該頻率是來自夾層空隙和底面反射信號形成。根據頻率與厚度的函數關系式(3)，脫空位置在10.5 cm 處，圖7b 中芯樣脫空位置大致在10.0 cm 附近；而底面反射波峰值頻率也為9.0 kHz，與實際情況相符。由此可見，沖擊回波信號受干擾波影響時，CEEMD 方法能正確識別出結構中的缺陷位置和混凝土厚度。

3 結論

1）CEEMD 方法能夠有效地將沖擊回波信號從含有嚴重的面波和噪聲干擾中分解為相應的IMF 分解為相應的IMF，IMF 模態函數頻率由高到低按序排列。

2）IMF 對應的頻譜顯示，高頻成份一般為噪聲干擾成份為主的面波信號，處于中間的IMF 則為夾層處缺陷和板底反射成份的信號。

3）分析缺陷和板底反射信號的對應IMF，確定缺陷和板底反射信號頻率，再由頻率準確計算內部夾層缺陷位置和混凝土板厚。

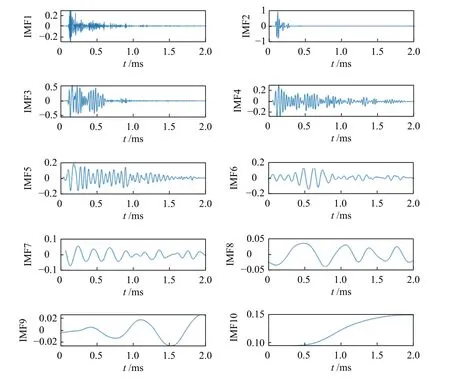
圖8 CEEMD 對現場測試信號分解的IMFFig.8 IMF decomposed on site testing by CEEMD

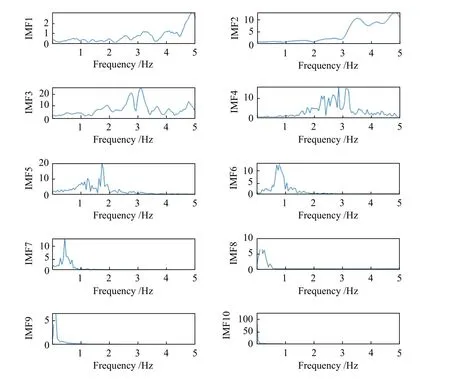
圖9 現場檢測信號的IMF1～IMF10 頻譜圖Fig.9 IMF1～IMF10 spectrogram on site testing signal