Entropy squeezing for a V-type three-level atom interacting with a single-mode field and passing through the amplitude damping channel with weak measurement*

Cui-Yu Zhang(張翠玉) and Mao-Fa Fang(方卯發(fā))

Synergetic Innovation Center for Quantum Effects and Applications,Key Laboratory of Low-dimensional Quantum Structures and Quantum Control of Ministry of Education,School of Physics and Electronics,Hunan Normal University,Changsha 410081,China

Keywords: entropy squeezing,V-type three-level atom,single-mode field,weak measurement

1. Introduction

Squeezing effect, as an effective method to suppress quantum noise in quantum systems, has attracted great attention during the last decades due to its potential application in optical communication,[1]detections of weak signal like a gravitational wave,[2]high-resolution spectroscopy,[3]the high-precision atomic fountain clock,[4,5]high-precision spin polarization measurements,[6]and the quantum information processing. It is well known that the research on squeezing effects mainly includes the generation of the squeezing and the measurement of the squeezing. As for the measure of squeezing, many studies[7–9]are based on the Heisenberg uncertainty relation,which is regarded as the standard limitation on measurements of quantum fluctuations. However, the variance squeezing(VS)based on the Heisenberg uncertainty has its own limitations in the following aspects. On the one hand,standard deviation only contains the second-order statistical moment for the state density matrix and the higher-order statistical moments are neglected.On the other hand,for some particular cases, the Heisenberg uncertainty relation is trivial and fail to provide any useful information. Fortunately,one of our authors[10]defines the entropy squeezing (ES) firstly for a two-level atom via quantum information entropy,which not only captures all information about the squeezed states and provides a general measure of the quantum uncertainty but also overcomes the limitations of the definition of the variance squeezing. Since the entropy squeezing was presented, its properties and schemes for generating entropy squeezing have been widely investigated. Xiao et al.[11]have studied the entropy squeezing properties of a two-level atom off-resonantly coupled to a non-Markovian reservoir. Yu et al.[12]have obtained the optimal and steady entropy squeezing of a two-level atom in a dissipative cavity under quantum-jump-based feedback and classical field. Via the non-Hermitian operation,Wang et al.[13]have provided a scheme for generating sustained optimal entropy squeezing of a two-level atom. However,all of the researches mentioned above are aimed at twolevel atom while there is little attention devoted to the entropy squeezing of three-level atom until Liu et al.[14]made a general definition of entropy squeezing for a Ξ-type three-level atom recently.

Nowadays, it is well known that quantum systems with higher dimensions may have lots of obvious advantages than ones with lower dimensions in quantum information processing,[15,16]since they provide higher channel capacities, more secure cryptography as well as superior quantum gates.[17–19]More importantly, compared with qubits, maximally high-dimensional entanglement states are less influenced by noise effects.[20]Motivated by the above-mentioned advantages and considering one of the author in Refs.[14]has present the entropy squeezing of the Ξ-type atom only,we focus our attention on the squeezing properties of a V-type threelevel atom in this paper. Firstly, we conduct a review of the definition of the entropy squeezing of three-level atom. Then we investigate the entropy squeezing of the V-type three-level atom in different conditions:one is interacting with the singlemode field while the other is in the noisy environment and under the control of the weak measurement technology. The numerical results show that when coupled to the single-mode field, the V-type atom can not only generate obvious squeezing entropy but also keep in the optimal entropy squeezing state if only the system is prepared in the appropriate initial state. While passing through the amplitude damping channel,the atom can also generate entropy squeezing via weak measurement with a certain strength.

The paper is organized as follows.In Section 2,we review the general definition of the entropy squeezing for a threelevel atom. In Section 3, we firstly investigate the entropy squeezing properties of a V-type three-level atom coupled to a single-mode field and compare it to variance squeezing. Then we analyse the effects of the weak measurement as well as measurement reversal on the atomic entropy squeezing when the V-type three-level atom is in noisy environment simulated by amplitude damping channels in Section 4. Finally, a brief summary is presented in Section 5.

2. Entropy squeezing for a three-level atom

Before analyzing the entropy squeezing properties of the atom in our systems,we firstly review the general definition of the entropy squeezing of a three-level atom given by Ref.[14].As is well known, a three-level atom can be described by dipole operators Sα(α =x,y,z), which satisfy the commutation relationship[Sx,Sy]=iSz. Besides,since the definition of the squeezing depends on them, we choose a universally adapted spin operators in this paper,which are shown as

Similarly with the definition of the variance squeezing,we start with the entropy uncertainty relation. Accordingly,the information entropy of the operators Sα(α =x,y,z)for a three-level atom is

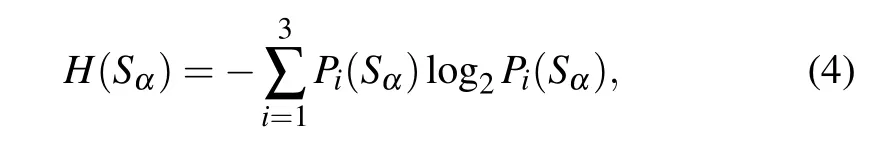
where Pi(Sα)=〈ψαi|ρ|ψαi〉(i=1,2,3)is the probability distribution for each possible outcome of measurement on the operator Sα,while ψαirepresents the eigenvector of the operator Sαand ρ is the density matrix for an arbitrary quantum state.The information entropies satisfy the entropy uncertainty relation for three observables of the system with dimension d=3 derived by Alberto et al.in Ref.[21]

Next, we will investigate the properties of the entropy squeezing for a V-type three-level atom.

3. Entropy squeezing for a V-type three-level atom

3.1. Entropy squeezing for a V-type three-level atom interacting with a single-mode field

In this section, the system we considered is a V-type three-level atom (here |0〉 is ground state while |1〉 and |2〉are two excited states) interacting with a single-mode field.The transitions between|0〉and|1〉,|0〉and|2〉are interacting with a single-mode field resonantly with interaction strength gj(j=1,2). In the interaction picture, the system Hamiltonian can be expressed as(=1)

where a is the annihilation operator of the field.For simplicity,we consider the resonant case between the atom and the field,for the atom initially in the superposition state

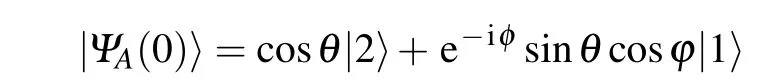
where

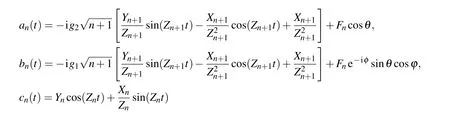
with

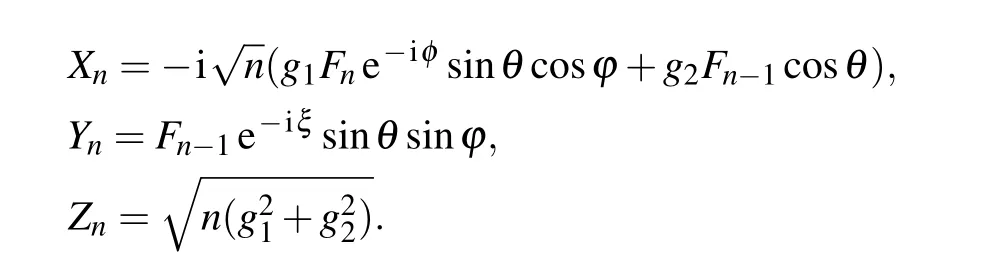
Accordingly, the atomic reduced density matrix can be given by

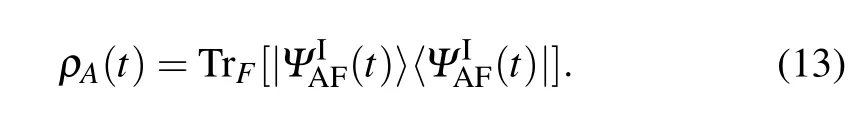
The elements of ρA(t)can be written as

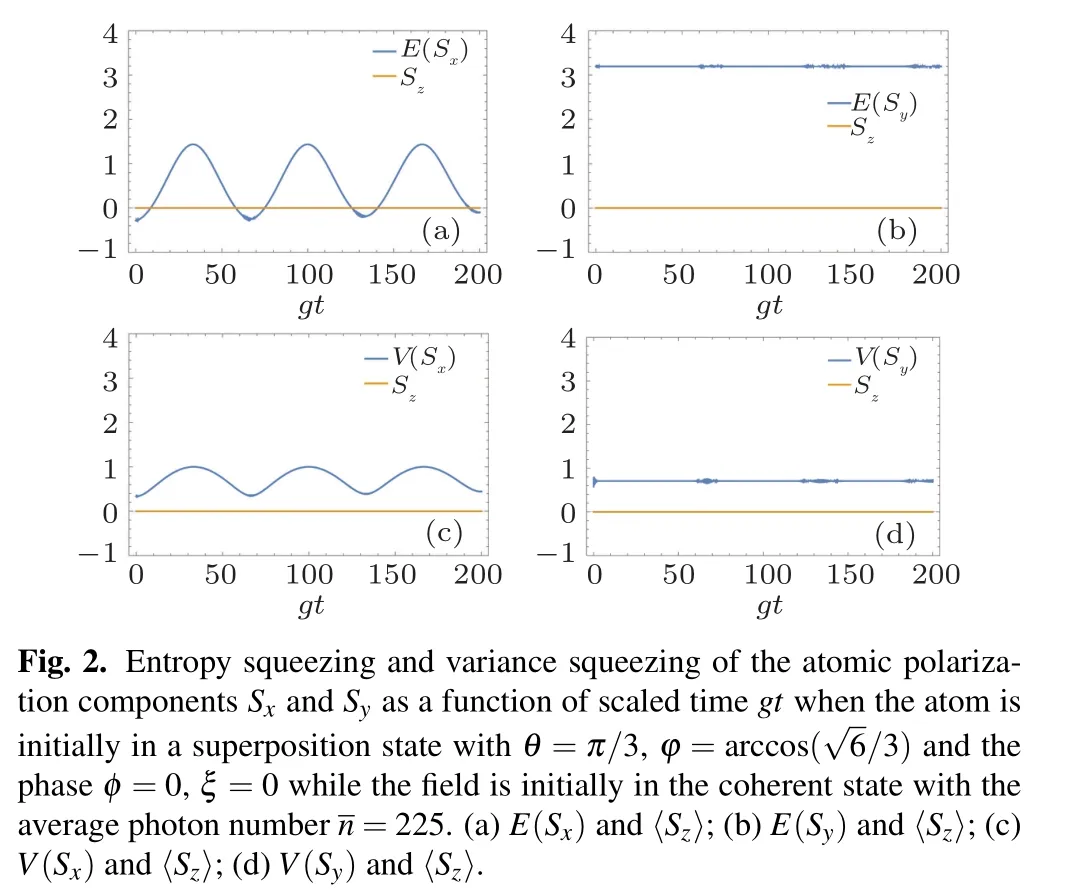
It is noted from Figs.2(c)and 2(d)that variance squeezing cannot predict squeezing information in neither Sxnor Sycomponents while the entropy squeezing can capture the squeezing information only in Sxcomponent in certain time ranges as shown in Figs.2(a)and 2(b). The reason is that the atomic inversion〈Sz〉keeps zero all the time so the Heisenberg uncertainty relation is trivial.

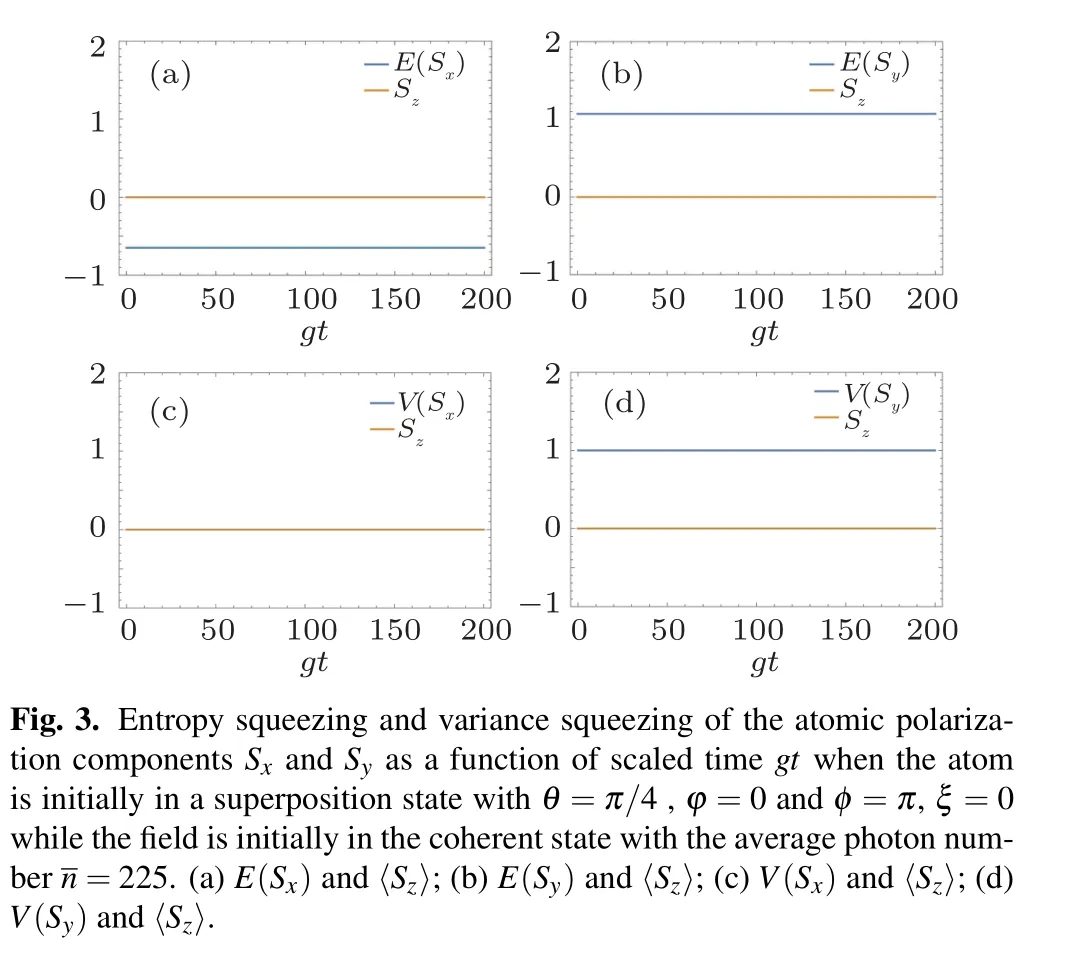
Finally, we prepare a special state initially, which is the superposition state of excited states |1〉 and |2〉 with different phase. By setting the parameters of the initial atom state:θ =π/4, φ =0, and the phase φ =π, ξ =0 while the other parameters are the same as those given before, we obtain the density matrix elements of the atom respectively

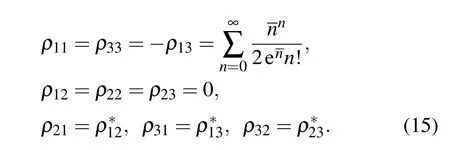
Substituting Eq. (15) into Eqs. (7), (8), and (3), the entropy squeezing factor and variance squeezing factor of the atom can be obtained. The results are shown in Fig. 3, from which we can see that although E(Sx), E(Sy), V(Sx), V(Sy), and 〈Sz〉all remain unchanged,there is an obvious difference between E(Sx)and V(Sx): the former stabilizes in the optimal squeezing while the latter predicts no squeezing at all for〈Sz〉keeps zero. In other words, when the atom is prepared in this optimal entropy squeezing state initially, the field can keep the atom in this optimal entropy squeezing state,which is a great advantage over the Ξ-type three-level atom in Ref. [14].

3.2. Entropy squeezing for a V-type three-level atom under the amplitude damping channel via weak measurement and measurement reversal

In this section,we investigate the entropy squeezing of a V-type three-level atom under decoherence simulated by amplitude damping channels via the control of the weak measurement and the measurement reversal at finite temperatures,before proceeding,we first review the knowledge of amplitude damping channels, the weak measurement, and the measurement reversal.

(i) Amplitude damping channel

As we know,the environment noisy can be simulated well by noisy quantum channels,under which various quantum effects have always been investigated widely.[22–24]The amplitude damping (AD) channel we considered is a dissipative channel with the probability r of losing the excitation,and the probability 1-r of absorbing the excitation,where 0 ≤r ≤1 is usually a function of temperature.[25]This process can be characterized by a quantum operation such that di(i = 1,2) represents the decoherence constant induced by the spontaneous emission of the exited state |i〉(i=1,2)to the ground state|0〉,respectively.

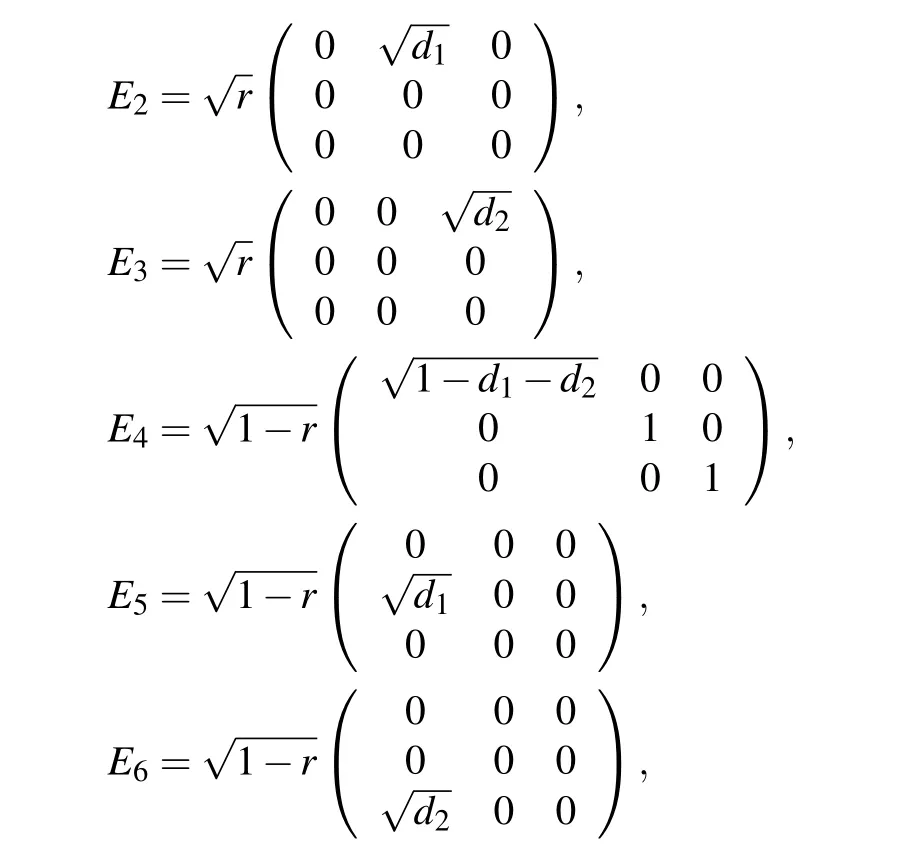
(ii) Weak measurement and measurement reversal protocol

In Fig.4,we show entropy squeezing for a V-type threelevel atom under decoherence at finite temperature by weak measurement technology. One can observe that when there is no weak measurement reversal (q=0), entropy squeezing can occur under control of weak measurement with certain strength. However,when there is only weak measurement reversal(p=0),there is no entropy squeezing at all,and it does not work even if both of the weak measurement and the measurement reversal (p=q) are used on the atom at the same time. This indicates that the weak measurement technology is more helpful than measurement reversal in generating the entropy squeezing.

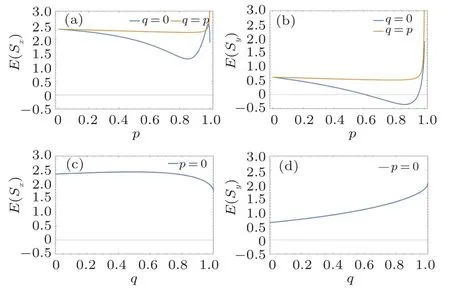
Fig.4. Entropy squeezing of the V-type three-level atom under decoherence via weak measurement and measurement reversal when the atom is initially in a superposition state with θ =π/8, φ =π/8, and φ =0, ξ =0. Other parameters are chosen to be r=0.9,and d1 =d2 =0.05. (a)E(Sx)versus the weak measurement strength p;(b)E(Sy)versus the weak measurement strength p;(c)E(Sx)versus measurement reversal strength q;(d)E(Sy)versus measurement reversal strength q.

4. Conclusion

Suppressing the quantum noise(quantum uncertainty)via squeezing effects is crucial for the development of the quantum information technology.To make contributions to prepare three-level system information resources with ultra-low quantum noise, we have discussed the squeezing properties of a V-type three-level atom interacting with the single-mode field or passing through the amplitude damping channels under the control of the weak measurement. First of all, by calculating the entropy squeezing of a V-type three-level atom interacting with a single-mode field, we found that the single-mode field in coherent state can keep the atom in the optimal entropy squeezing state when the atom is initially in the eigenstate of Sx,which can be interpreted by the steady-state solution shown in Eq. (15); And we also studied the variance squeezing for comparisons, which demonstrates the general validity of the entropy squeezing as a measure of quantum uncertainty. Then under the help of the weak measurement, the V-type threelevel atom exposed to amplitude damping channel can generate obvious entropy squeezing in appropriate initial atomic state. That is to say,the weak measurement technology is effective in the generation of squeezing effect via suppressing quantum noise, which is meaningful for the suppression of quantum noise with current experimental capabilities.