基于高斯混合聚類的風電出力場景劃分①
張發才,李喜旺,樊國旗
1(中國科學院 沈陽計算技術研究所,沈陽 110168)
2(中國科學院大學,北京 100049)
3(國網金華供電公司,金華 321001)
近年來,中國風力發電發展速度快,風電場的規模以及風電并網比例不斷增大.與傳統的發電方式相比,風力發電最根本的不同點在于其有功出力的隨機性、間歇性和不可控性[1].由于地理地貌和季風變化影響著風電資源分布,風電出力的隨機性變化具有一定的季節周期性[2],用典型場景集反映周期內風電出力的變化特征,對含有風電電力系統的規劃和調度具有重要意義.
目前,風電出力典型場景的選取主要采用聚類劃分方法.文獻[3]介紹了聚類算法大致可以分為層次聚類算法,劃分式聚類,基于密度和網格的聚類算法和其他算法.文獻[4]提出基于改進K-means 聚類的風電功率典型場景.文獻[1]采用改進的模糊C 均值聚類算法和分層聚類算法,實現對風電出力場景的選取.文獻[5,6]采用K-means 算法對風電出力樣本進行聚類劃分,得到具有代表性的典型風電出力場景.文獻[7]提出基于Wasserstein 距離和改進 K-medoids 聚類算法,構建覆蓋調度空間的典型場景.文獻[8]提出主成分分析法和分層聚類算法相結合的方法,計算出年度典型風電出力場景.文獻[9]采用模糊C 均值聚類法,完成對所研究區域風電功率典型場景的提取.
以上聚類算法都是以歐氏距離作為樣本相似度判斷,歐氏距離能反映樣本曲線間的遠近程度,不能反映曲線形態的相似程度.文獻[10]提出基于考慮序列互相關性的“形態距離”的聚類算法,并提取春,夏,秋,冬的風電出力典型場景,避免了基于歐式距離聚類的缺點.文獻[11]比較得出GMM (Gaussian Mixture Model)聚類質量優于層次聚類,K-means,K-medoids,SOM 聚類.文獻[12]提出基于高斯混合模型的公交出行特征分析.文獻[13]通過應用高斯混合模型對伊朗西南部某水域進行分區,取得很好的效果.文獻[14]提出基于EM 和GMM 的樸素貝葉斯巖性識別,結果表明高斯混合模型有很好的擬合效果.文獻[15]采用GMM聚類進行漢語數字識別.此外,GMM 聚類不僅具有靈活的類簇形狀,還能夠很好的捕獲屬性之間的相關性和依賴性[16].
本文提出了一種基于概率分布的高斯混合聚類模型GMM,通過樣本屬于某一類的概率大小來判斷其歸屬類別,本文選取某地區的風電出力情況,與傳統的基于歐式距離的聚類算法的劃分結果對比分析,驗證本文提出的風電出力場景劃分方法的有效性.
1 基于高斯混合聚類對風電出力場景的劃分方法
1.1 高斯混合聚類模型
高斯混合模型是由有限個獨立的多元高斯分布模型線性組合而成,每一個多元高斯分布成為混合高斯模型的成分,而多元高斯分布則是一元高斯分布在高緯度空間中的擴展[17].
假設一天內每個小時的風電功率為xi(i=1,2,···,24),則高斯混合模型可以表示為:
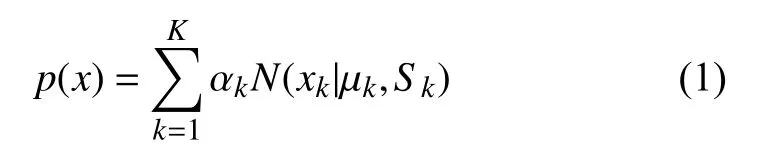
高斯混合模型有3 個參數需要估計,分別為μ,α和S,其中,μ 表示模型的期望,α表示各個分布的權重,S表示模型的方差.
上式可化為

下面采用最大似然法(EM)進行參數估計.
算法步驟如下:
(1)指定μ,α 和S的初始值.
(2)計算后驗概率γ (znk):

(3)求解μk的最大似然函數:

(4)求Sk的最大似然值

(5)求解 αk的最大似然函數

(6)循環重復計算步驟(2)~(5),直至算法收斂.
1.2 最佳聚類數目確定方法
對于最佳聚類個數確定,GMM 聚類往往是采用BIC 準則[18].貝葉斯信息準則(Bayesian Information Criterion,BIC),1978年由Schwarz 提出,用于實際中選擇最優的模型,如式(7):

其中,k為模型參數個數,n為樣本數量,L為似然函數,kln(n)懲罰項在維數過大且訓練樣本數據相對較少的情況下,可以有效避免出現維度災難現象.
對于K-means 聚類,采用肘部法則和輪廓系數相結合的方法確定最佳聚類數目.肘部法則的核心指標是誤差平方和(Sum of the Squared Errors,SSE),如式(8):
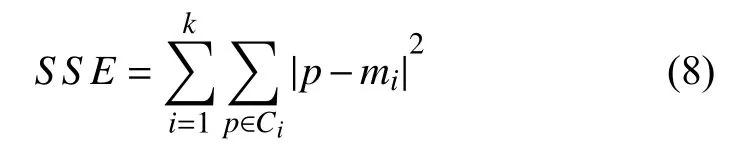
其中,Ci是第i個簇,p是Ci的樣本點,mi是Ci的質心,SSE是所有樣本的聚類誤差,代表了聚類效果的好壞.
當k小于真實聚類數時,由于k的增大會大幅增加每個簇的聚合程度,故SSE的下降幅度會很大,而當k到達真實聚類數時,再增加k所得到的聚合程度會迅速變小,所以SSE的下降幅度會驟減,然后隨著k值的繼續增大而趨于平緩,SSE和k的關系圖是一個手肘的形狀,而這個肘部對應的k值就是數據的真實聚類數
輪廓系數是類的密集與分散程度的評價指標,如式(9):

其中,a表示樣本到彼此間距離的均值,b表示樣本到除自身所在簇外的最近簇的樣本的均值,s取值在[?1,1]之間,如果s 越接近1,代表所在簇合理,如果s越接近?1,s應該分到其他簇中.對于使用輪廓系數確定聚類的數量,應該選取較大的輪廓系數.
2 實驗和結果分析
風電出力通常具有明顯的季節分布特性,與單風電場相比,一個地區的風電功率具有更明顯的季節性規律.
首先選取某地區2017年至2019年3年春季3 個月的每1 小時實測地區風電出力數據進行分析,驗證該方法的有效性,然后再對該地區其他季節風電出力特性進行分析.
2.1 最佳聚類數目確定
使用BIC對高斯混合模型進行選擇,既涉及協方差的類型,也涉及模型中聚類的數量.如圖1所示,其中spherical,tied,diag,full 分別對應球面協方差矩陣,相同的完全協方差矩陣,對角協方差矩陣,完全協方差矩陣,GMM 應選擇聚類數目為4 的和相同的完全協方差矩陣.
針對K-means 聚類,綜合考慮SSE和輪廓系數,如圖2所示,藍色曲線表示SSE隨著k變化的曲線,紅色曲線表示輪廓系數隨著k變化的曲線.一般來說,平均輪廓系數越高,聚類的質量也相對較好.在這,最優聚類數應該是2,這時平均輪廓系數的值最高.但是,聚類結果(k=2)的SSE值太大了,根據肘部法則,當k=4 時,SSE的值會低很多,但此時平均輪廓系數的值較高.因此,k=4 是最佳的選擇.
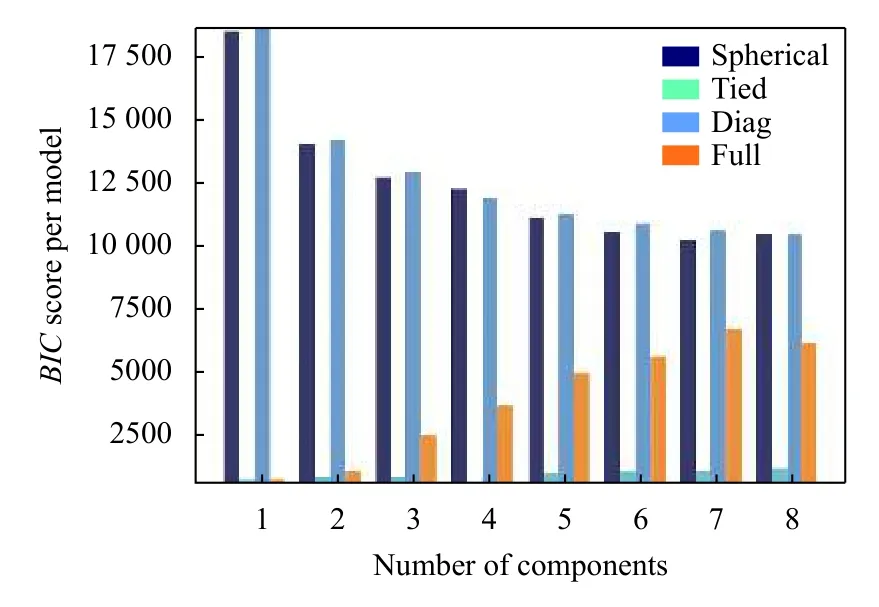
圖1 混合高斯模型參數選擇

圖2 K-means 聚類模型的k 選擇
2.2 基于概率的聚類劃分
圖3中,紅色曲線為聚類中心,代表該地區風電風力的典型場景.在4 種形態的樣本簇中,每一簇的風力出力功率范圍明顯不同,大部分的類內樣本都與聚類中心相似,只有少數曲線的形狀與中心曲線的形態不同.
2.3 基于歐式距離的聚類劃分
采用K-means 聚類算法對同一組數據進行聚類劃分,得到的風電出力曲線簇如圖4所示.
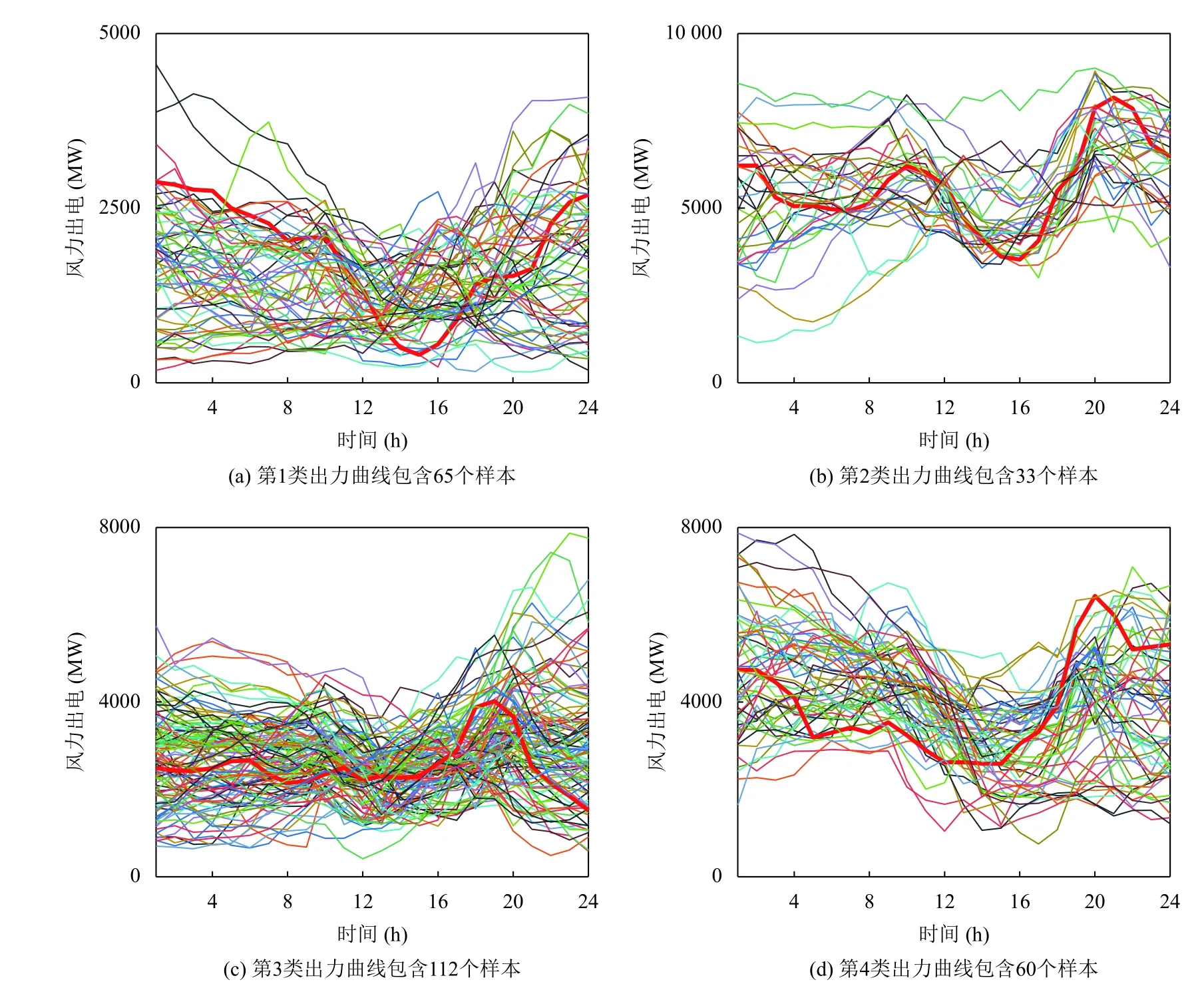
圖3 4 類風電出力曲線簇(GMM)
紅色曲線為聚類中心,代表該地區風電風力的典型場景.如圖4所示,類內包含多種形態的出力曲線,很多曲線形態與聚類中心曲線形態不一致,僅能反映出風電出力的幅度大小.
為進一步比較這兩種聚類方法,分別提取其聚類中心曲線.
在圖5中,從峰谷差分布范圍來看,基于K-means算法風電功率峰谷差分布范圍集中在1700-3300 MW之間,不能反映出風電峰谷差特點,對調度安排實用價值較小.基于GMM 聚類算法風電功率分布范圍從2400-4600 MW 之間,較能反應該地區風電峰谷差波動范圍.
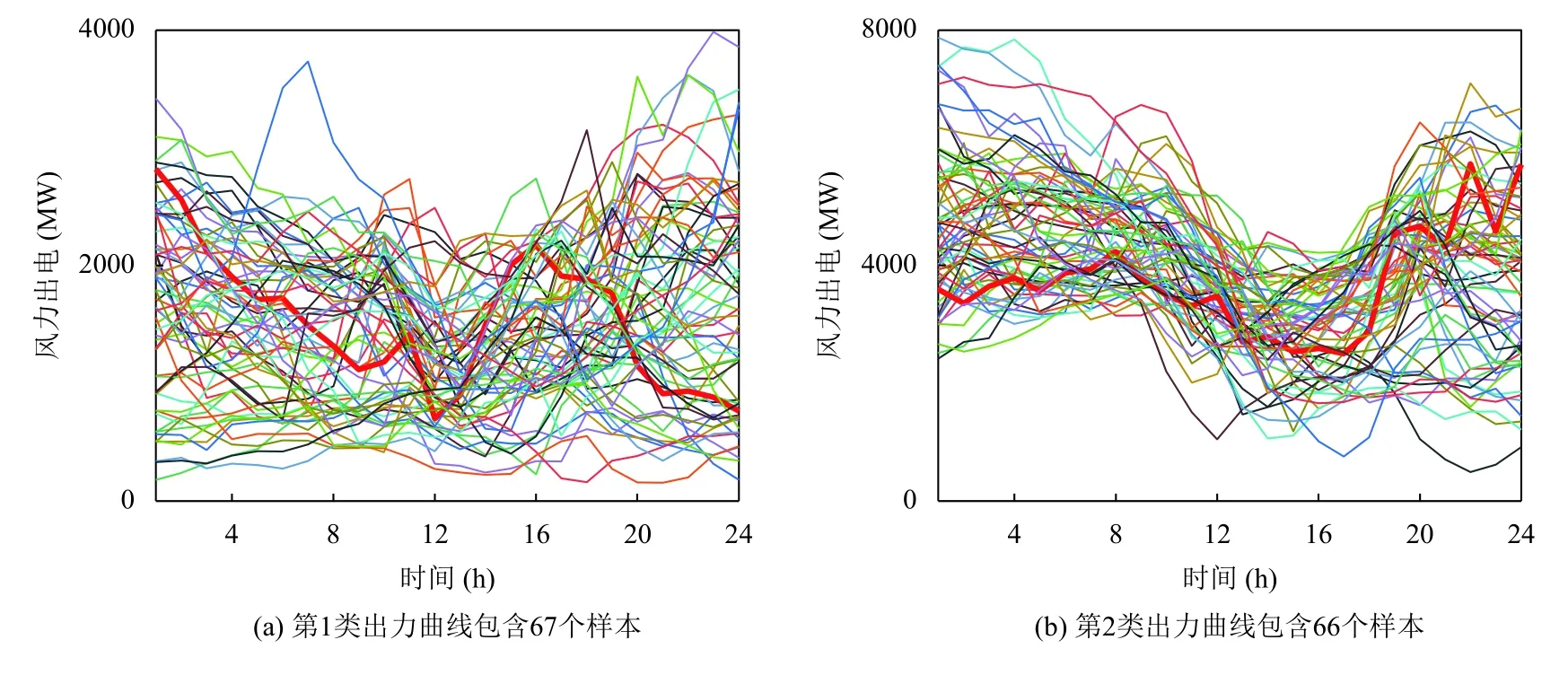

圖4 4 類風電出力曲線簇(K-means)

圖5 GMM 與K-means 聚類中心曲線對比
從功率波動范圍來看,K-means 波動范圍較小,不能反映某些情況下風電的大范圍波動特點、多峰谷特點(如GMM 第2 類出力)以及正反調峰特點(K-means風電波動特征選取較差).
3 其余季節風電出力場景
對于夏、秋、冬季節,使用BIC對高斯混合模型進行選擇,得到最佳聚類數目應為3.提取這3 個季節的風電出力場景,圖6到圖8分別為夏、秋、冬季的場景曲線簇,其中,紅色曲線代表該季節風電出力的典型場景.


圖6 夏季地區風電出力場景曲線簇
由圖9可知,該地區夏秋季節風電出力功率較大、功率波動范圍分布變化較小、功率波動范圍較大,夏季上半日相比秋季風電波動較小;冬季風電波動與春季相似,但呈現多峰谷特點更加明顯.
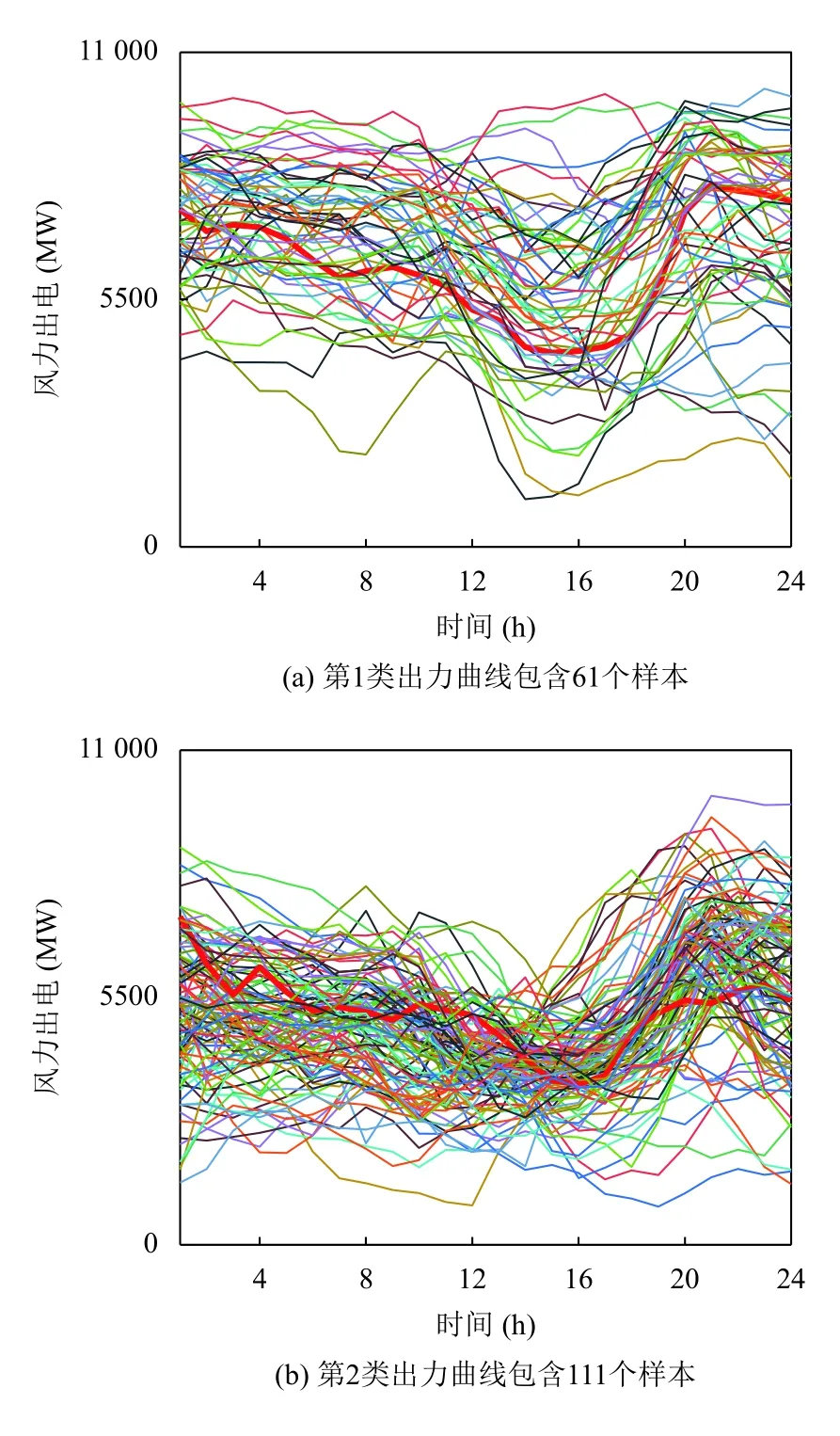
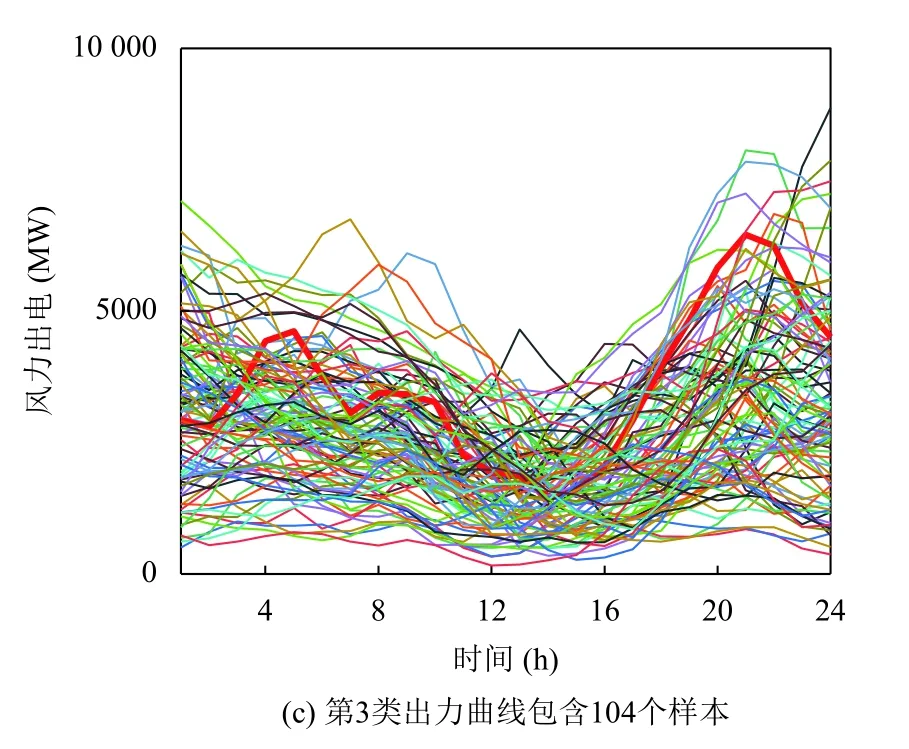
圖7 秋季地區風電出力場景曲線簇
在調度計劃中,夏秋季節應安排調峰能力較強機組和其他調峰資源,應對風電功率大范圍波動,且秋季上半日應多安排爬坡性能較高機組或靈活性調節資源,應對風電功率頻繁波動.針對春冬季節風電多峰谷特性對峰谷電價合理優化,通過負荷參與電網調度減少風電峰谷差.

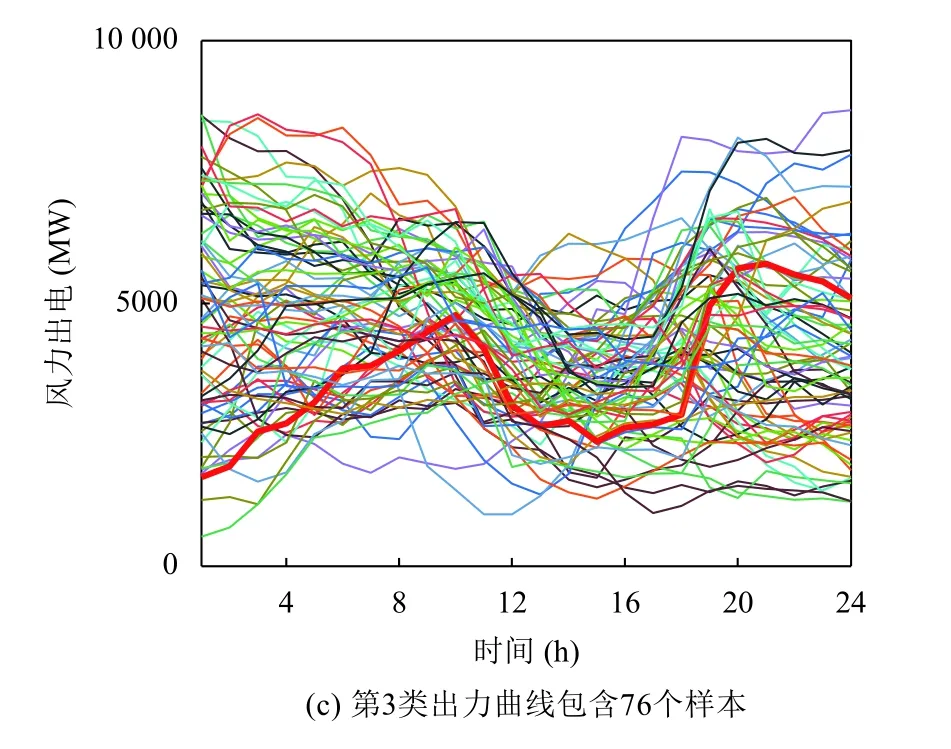
圖8 冬季地區風電出力場景曲線簇
4 結論
隨著清潔能源在社會發展中扮演越來越重要的角色,風能資源的利用也逐漸增多.本文針對風電出力場景進行研究,提出的高斯混合聚類模型,能夠提取典型風電出力場景,并與K-means 聚類方法對比,該文提取的方法更能得到同類形態相近的曲線,反映出風電功率變化的特征,例如風電的正反調峰特性和波動特性,對電網的調度具有重要意義.

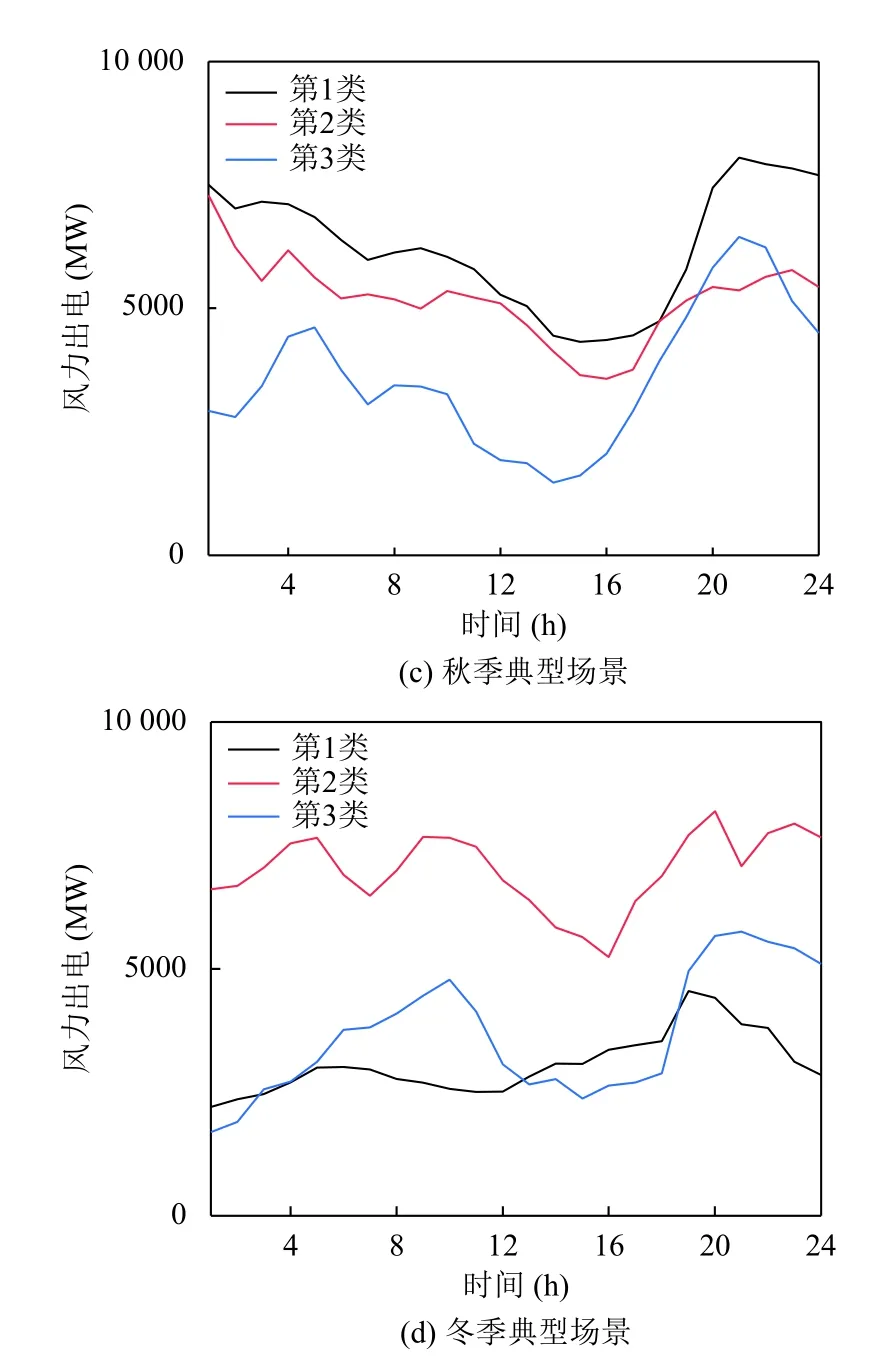
圖9 四季曲線簇的典型場景

