無限深勢阱問題的可視化研究
肖光延,陳鳳翔,汪禮勝
(武漢理工大學 理學院物理科學與技術系,湖北 武漢 430070)
無限深勢阱是量子力學研究與教學中的經典問題,通常人們所關心的是這些無限深勢阱的薛定諤方程如何求解,以及所解出的“定態”的概率分布可視化.前者的研究已經十分成熟,現有的教材和習題中均有涉及[1]1,2],而后者尤其是三維勢阱的可視化研究還是比較少見的.張春國[3]和楊紅衛[4]等利用Matlab給出了三維無限深方勢阱波函數和概率密度的切片圖,這不失為一種可行的方式,但對于一些更加復雜的圖案仍有一定的局限性.本文對其做出改進,繪制了電子云圖像,并成功將其應用在了柱形勢阱和球形勢阱之中.將無限深勢阱中粒子的量子行為可視化,可以有效輔助教學,幫助學生理解相關抽象概念,對量子力學理論的教學大有裨益[4].
1 無限深方勢阱
1.1 一維無限深方勢阱的求解及推廣
一維無限深方勢阱可以說是最經典的模型,該勢阱實際中并不存在,但在一定條件下,很多系統都可以抽象成無限深勢阱問題來處理,如量子點、量子線段等[5].其勢阱可以簡單描述為
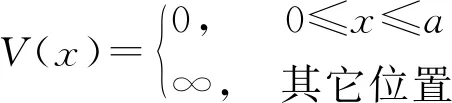
(1)
這個勢阱的定態解為
(2)
(3)
其中,m=1,2,3,….
以上結論可以直接推廣到二維和三維的情況,對于二維勢阱,有
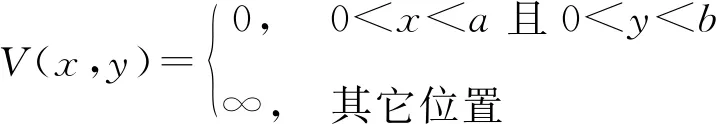
(4)
(5)
(6)
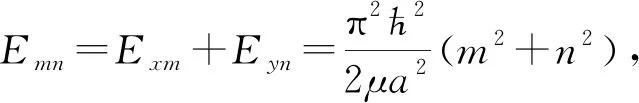
對于三維勢阱,則對應的波函數和能級分別為
(7)
(8)
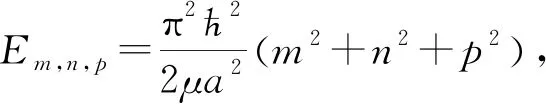
1.2 無限深方勢阱可視化
借助Matlab軟件中強大的計算和顯示功能,我們依托GUI界面開發了無限深勢阱顯示界面,可以通過下拉菜單選擇一維勢阱、二維勢阱和三維勢阱,同時在不同勢阱模型下又可以進行細分,如二維勢阱可以細分為方形和圓形勢阱等.然后在不同方向選擇合適的量子數,點擊“運行”即輸出此時的空間波函數和概率密度圖.
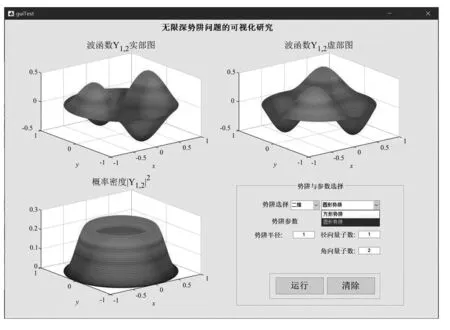
圖1 GUI主界面圖

二維和三維圖像也有類似規律,分別如圖3和圖4所示,他們的概率密度或者電子云圖像在某一方向上的“峰值”的個數總是等于這個方向上的量子數.圖3中給出了幾個二維無限深方勢阱中的波函數及對應的概率分布,其中圖(a)、圖(b)、圖(c)分別對應Ψ21、Ψ12和Ψ13情形,其中上部分為波函數分布,下部分為概率密度.從圖3(a)中可以看出,二維波函數Ψ21在x方向有兩個極值,而y方向僅有1個極值,在概率密度分布中x方向出現了2個峰值,而y方向只出現了1個峰值.對其他2種情形可進行類似分析.
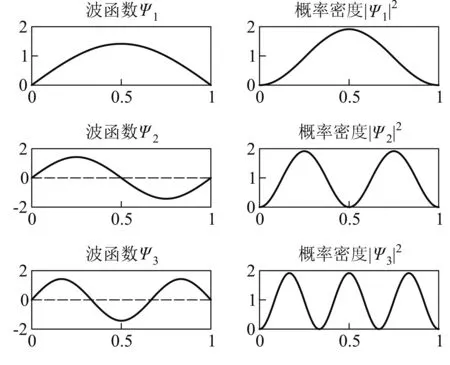
圖2 一維無限深方勢阱前3個波函數及其概率密度
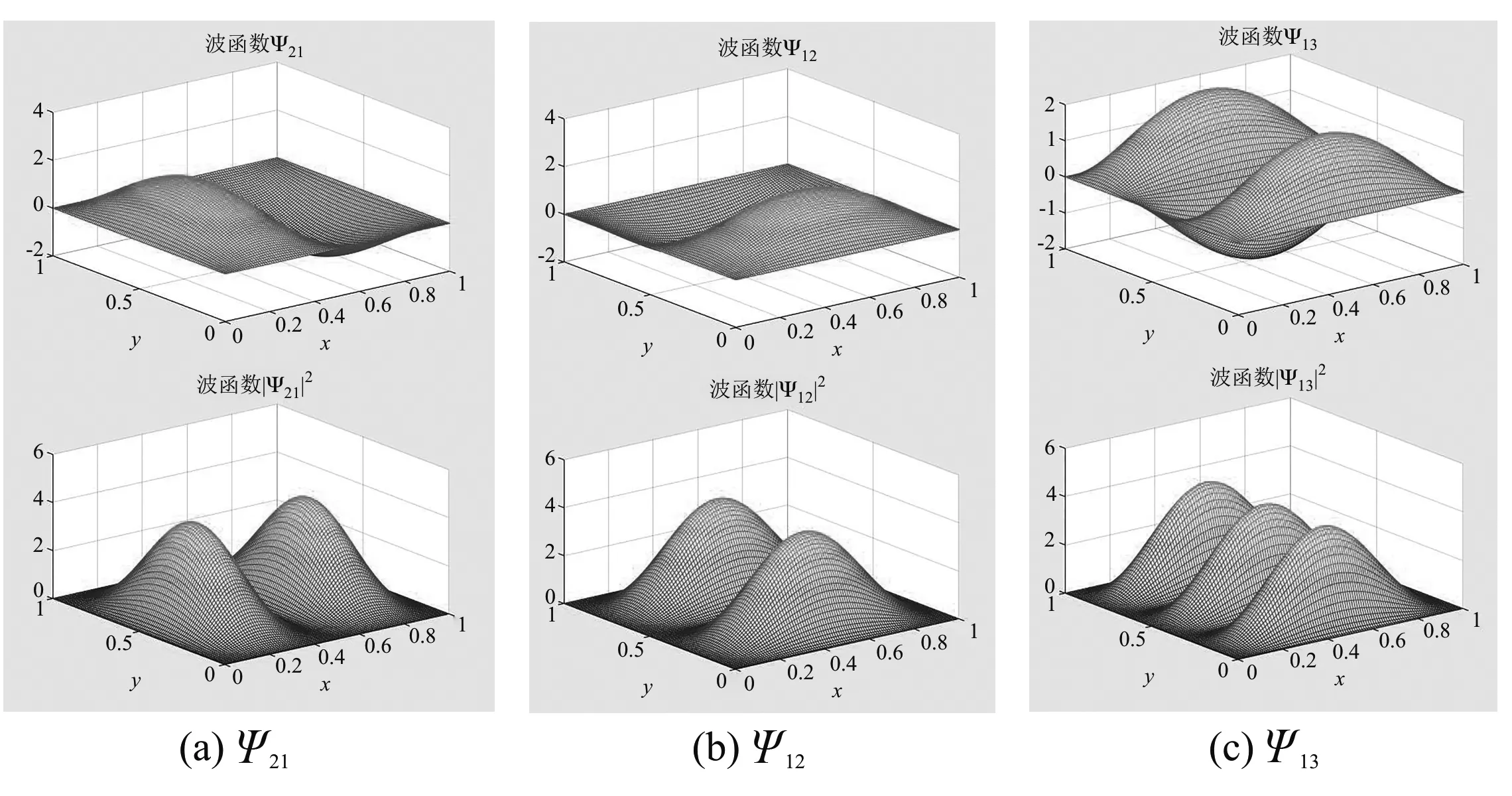
圖3 二維無限深方勢阱的幾個波函數及其概率密度

圖4 三維無限深方勢阱Ψ212電子云圖像
對于三維無限深勢阱中的波函數,我們采用電子云來描述,以圖4中Ψ212的概率分布為例.|Ψ212|2在空間形成了四朵云,保證了概率密度在x方向出現2個峰值,y方向有1個峰值,z方向存在2個峰值.
2 無限深圓形勢阱和柱形勢阱
2.1 二維無限深圓形勢阱的求解及其推廣
二維無限深圓形勢阱可以表述為
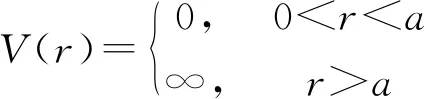
(9)
粒子被束縛在勢阱之中,在邊界上有無窮大的力限制它逃逸,而在勢阱內部,它是自由的.在銅(Cu)表面量子圍欄的研究中,組成圍欄的48個鐵(Fe)原子將Cu表面態電子禁錮其中,形成同心圓駐波,該體系就可以抽象為二維無限深圓形勢阱[8,9].圓形勢阱內部的哈密頓量為[1]
(10)
考慮分離變量法,令哈密頓量的本征態為Ψm(r,θ)=R(r)Φm(θ).采用數學方法求解,則二維無限深圓勢阱中的波函數
Ψn,m(r,θ)=J|m|(ηn,|m|r)Φm(θ)=
(11)
其中J(r)為貝塞爾函數[10].可以看出,能級是二重簡并的(m=0除外),m取正取負雖表示著不同的波函數,卻有著相同的能量.
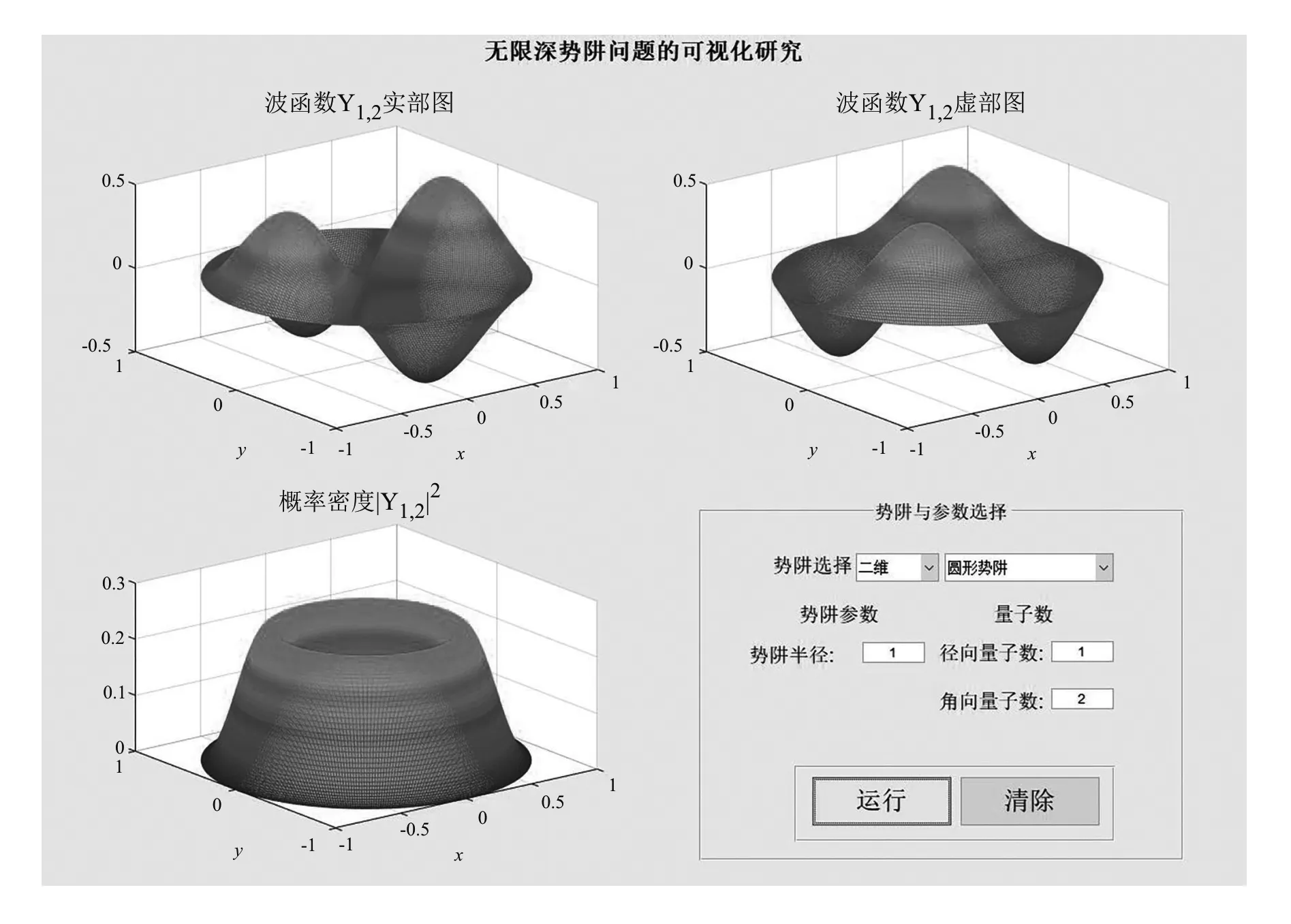
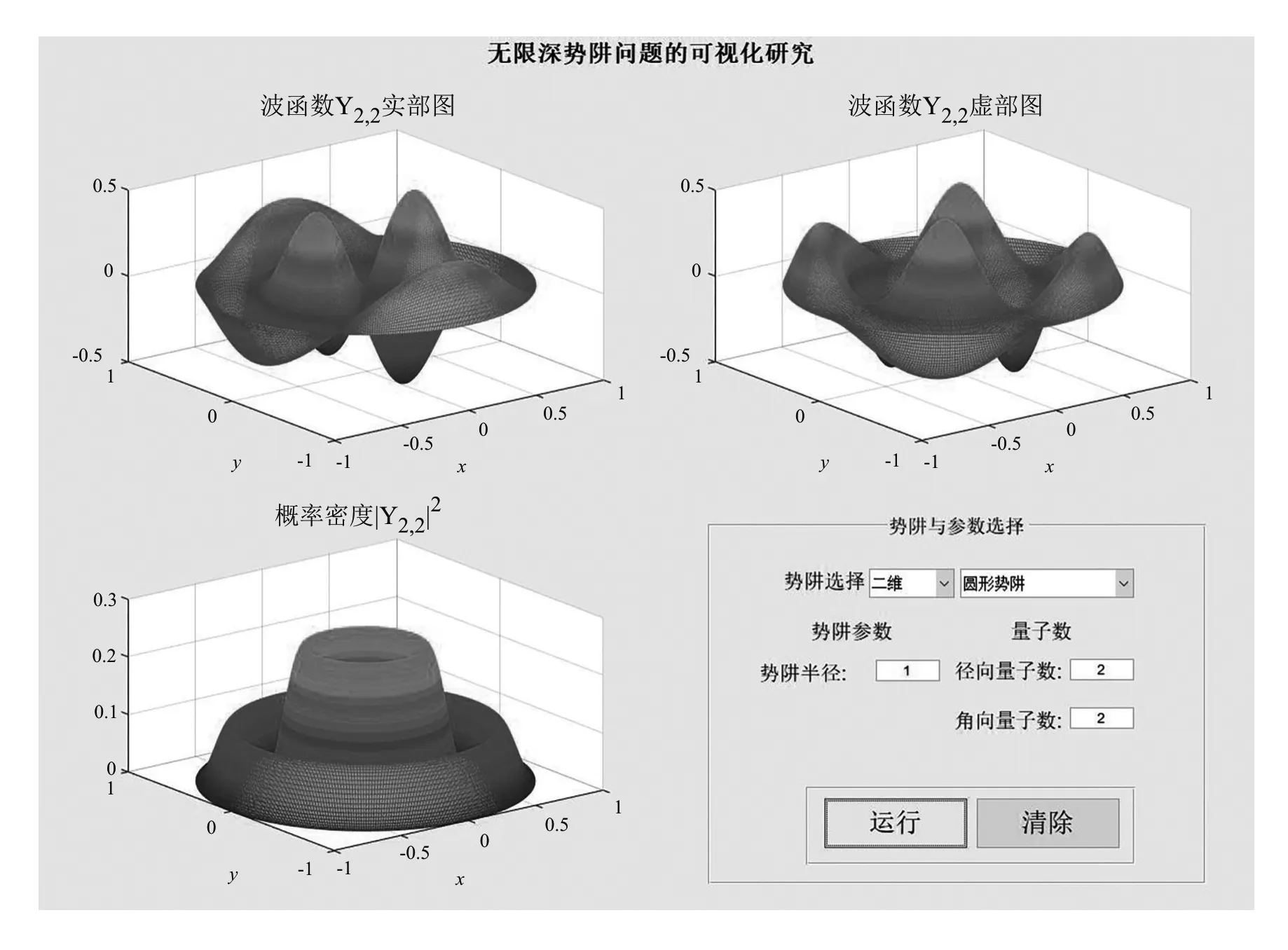
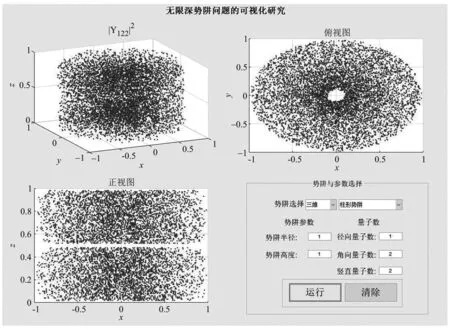
如果考慮柱形勢阱,那只不過是在豎直方向上多了一個一維無限深勢方阱,粒子被約束在0 (12) 而對應的能量本征值 (13) 此時能級仍然為二重簡并. Ψ12的波函數和概率密度 Ψ22的波函數和概率密度 無限深柱形勢阱在水平方向上的變化規律和圓形勢阱相同,而在豎直方向上的變化規律則和一維無限深方勢阱相同,圖6是其電子云圖像. Ψ122的電子云圖像 Ψ222的電子云圖像 圖6(a)和(b)分別是柱形勢阱中粒子處于態Ψ122和Ψ222時的概率分布,從正視圖中可以看出,他們都在空間中分成了上下兩層,這保證了概率密度在z方向上出現2個峰值.此外,圖6(a)中俯視圖展示了|Ψ122|2在水平方向上有1個同心圓環,而圖6(b)中俯視圖展示了|Ψ222|2在水平方向上的2個環,這是由徑向量子數n控制的,我們已經在二維的分析中提到了其原因. 三維無限深球形勢阱可作為原子核內勢能的一個高度簡化的物理模型[11],勢函數表示如下 (14) 在勢阱內,哈密頓算符可以寫成[1] (15) 要求解的波函數應該是(H,l2,l)的共同本征函數,它必然有著如下形式 (16) 分兩部分討論,當l=0時,m只能為0,這個時候的定態波函數為 (17) (18) 該能級無簡并. 當l≠0時,方程的解為 (19) (20) 可見,能級E只與n、l有關,因此,這個能級的簡并度取決于m,由于m=0,±1,±2,...,±l,因此簡并度為2l+1. 無限深球形勢阱概率分布隨3個量子數n、l、m變化的規律如圖7所示.在波函數中,半整數階貝塞爾函數和球諧函數互相調制,粒子在勢阱中的概率分布受兩者共同影響.因為貝塞爾函數電子云分布有了球殼結構,球殼的層數就是量子數n,同時粒子的概率分布又保留了球諧函數的大部分特征. 圖7中的(b)、(c)、(d)圖均可以看做是由半整數階貝塞爾函數和球諧函數互相調制而成.由于n=2,它們的電子云都有著2層的結構.而圖(b)的紡錘形,圖(c)的中間大環,圖(d)俯視圖中的零點,都是來自于對應的球諧函數的特征. 為進一步分析,在圖8中給出了三維無限深方勢阱|Ψ220|2以及構成它的徑向函數|Rl|2與球諧函數|Ψ20|2.從圖8(a)、(b)、(c)的對比中,我們可以直觀地看出|Ψ220|2既保留了|R2|2的兩層球殼結構,又可以從中看出|Ψ20|2的輪廓. Ψ100的電子云圖像 Ψ210的電子云圖像 Ψ220的電子云圖像 Ψ221的電子云圖像 |Ψ220|2 徑向函數|R2|2 球諧函數|Ψ20|2 本文共介紹了一維、二維、三維等6個無限深勢阱的理論計算和可視化模擬,這基本上已經涵蓋了所有的規則勢阱.對于每一個勢阱,我們都對其波函數、概率密度以及電子云圖形隨量子數變化的趨勢進行了討論,此外,還分析了二維、三維勢阱的能級簡并度等.借助Matlab軟件的強大功能,粒子在勢阱中的概率分布變得直觀,有些圖像作出來后令人眼前一亮,使人不由地贊嘆對稱之美.無限深勢阱中波函數的直觀可視化,對量子理論的課堂教學及學生對量子力學中抽象概念的理解和掌握都具有很大幫助.2.2 無限深圓形勢阱和柱形勢阱的可視化
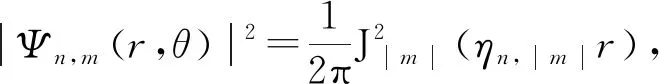

3 無限深球形勢阱
3.1 三維無限深球形勢阱的求解

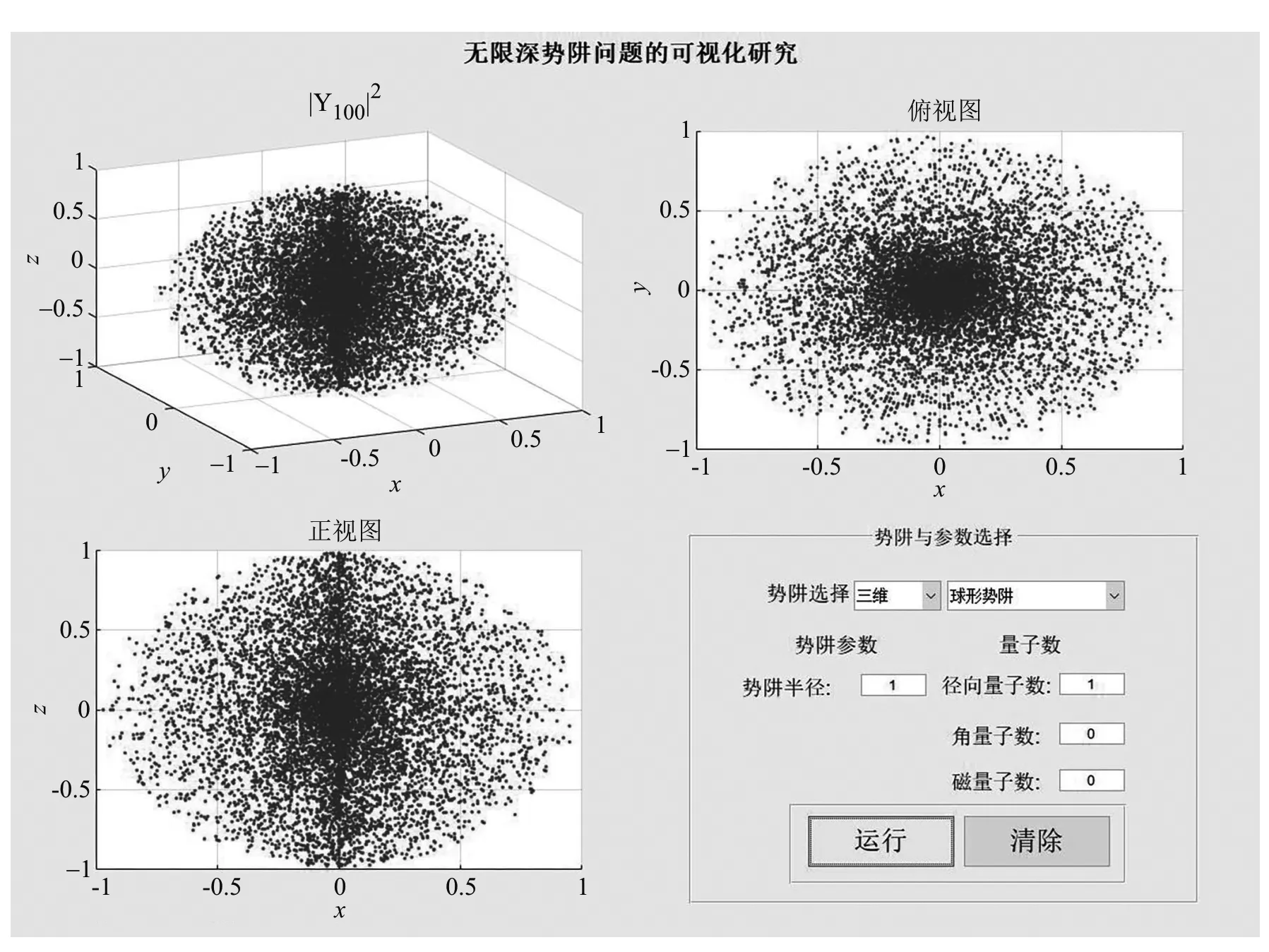
3.2 無限深球形勢阱的可視化
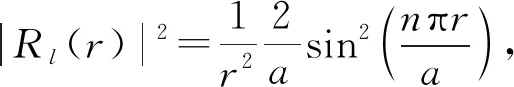






4 總結

