基于Gabor函數變換的棉花疵點檢測技術的研究

Gabor濾波器在織物疵點檢測中已經有著廣泛的應用，是一種非常好的特征提取算法。常見原棉疵點的形狀一般為點狀型、線狀型和聚集狀型等，而原棉為云狀型。所以原棉和其常見疵點在形狀輪廓上存在明顯差異，因此基于Gabor函數變換得到的Gabor濾波器適用于棉花疵點的檢測。

棉花疵點主要有破籽、索絲、僵片、棉結、不孕籽、軟籽表皮、帶纖維籽屑等。目前棉花疵點的檢測一般采用人工方法，該方法成本高，效率低，檢測準確性受人為主觀因素影響大，同時體積較小或者顏色接近白色的疵點很難被檢測出來[1]。考慮到成本投入、檢測的速度和準確率，顯然機器視覺比其他方法更加適用于棉花疵點的檢測。

Gabor濾波器在織物疵點檢測中已經有著廣泛的應用，是一種非常好的特征提取算法。常見原棉疵點的形狀一般為點狀型、線狀型和聚集狀型等，而原棉為云狀型。所以原棉和其常見疵點在形狀輪廓上存在明顯差異，因此基于Gabor函數變換得到的Gabor濾波器適用于棉花疵點的檢測。

1 Gabor函數和二維熵原理

1.1 Gabor函數相關原理

Gabor函數由D.Gabor首次提出，Daugman將其擴展為二維形式的同時，第一次將Gabor函數作為一種表征圖像的方法進行了應用，經試驗證明，這是一種較好的圖像特征提取算子[2]。二維Gabor函數的優勢在于其在獲得較高頻域分辨率的同時，能夠獲得較高的時域分辨率。而不用為了提高其中一個分辨率而犧牲另外一個分辨率[3]。其空間函數一般表達式為：

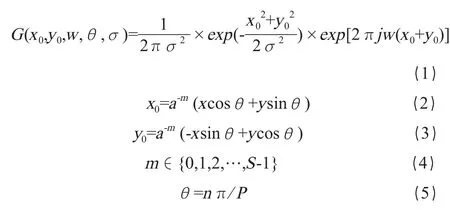
式（1）中，G為Gabor函數空間函數，x和y為圖像I（x，y）像素點的空間位置；w為濾波器中心頻率；為濾波器方向；為高斯函數沿坐標軸的標準方差；a-m為尺度因子；m為尺度參數；S為尺度總數；n為方向參數；P為方向總數。式（2）～式（5）是對參數的補充說明。濾波器的特性主要由m和n的值決定，根據不同的實際情況和應用環境，設計相適應參數組[m，n]的值，可以得到合適尺度和方向的Gabor濾波器來進行特征提取。

1.2 二維熵相關原理

熵是物理學中的基本概念，在信息論中，熵代表的是體系的混亂程度。熵的值越小，代表體系越穩定。而圖像體系越穩定，代表圖像中攜帶的有用信息越多[4]。圖像灰度分布的聚集特征可以引入一維熵來進行表征，但是其局限在于其無法表征灰度分布的空間特征。所以為了表征灰度分布的空間特征，引入了二維熵的概念。二維熵在一維熵的基礎上進行了擴展，以圖像中像素點的鄰域灰度均值i和像素灰度j組成特征二元組（i，j）來進行模擬計算。

式中，Pij為像素點分布的綜合特征，包含其灰度值以及其周圍像素的灰度分布，是一個綜合指數；f(i，j)表示特征二元組出現的次數；M表示圖像的尺度。用H來表示圖像的二維熵值，其數學表達式如式（7）：

2 算法設計

2.1 圖像的獲取和預處理

因為存在如噪聲干擾、光照不勻等因素的影響，所以原始圖像需要進行預處理，來提高圖像的質量，方便更好地獲取所需的信息。事實上，光照不勻一直是圖像處理中亟待解決的問題，極大地影響了最后的檢測結果。國內外研究人員一直試圖找到保持光照不變性的函數，但是收效甚微，大多數情況下只能根據不同的情況選取不同的方法進行光照補償。綜合考慮算法的時效性和實用性，本文選取直方圖均衡法來進行圖像的預處理，從而進行光照不勻的矯正，減少光照不勻對后期檢測結果的不良影響。

獲取多組含疵點的原棉圖像，將所有的圖像大小統一為512×512像素。將原始圖像轉換為灰度圖像后，對其進行直方圖均衡化處理，增強圖像像素的動態范圍，減少光照不勻的不良影響；接著對均衡化后的圖像進行高斯濾波處理，剔除一些不必要的噪聲干擾。完成預處理后的圖片記作I（x，y）。圖1分別給出了示例獲取的原始圖像及經過不同預處理步驟后的圖像。圖2為獲取的原始圖像及經過不同預處理步驟后圖像的灰度直方圖。

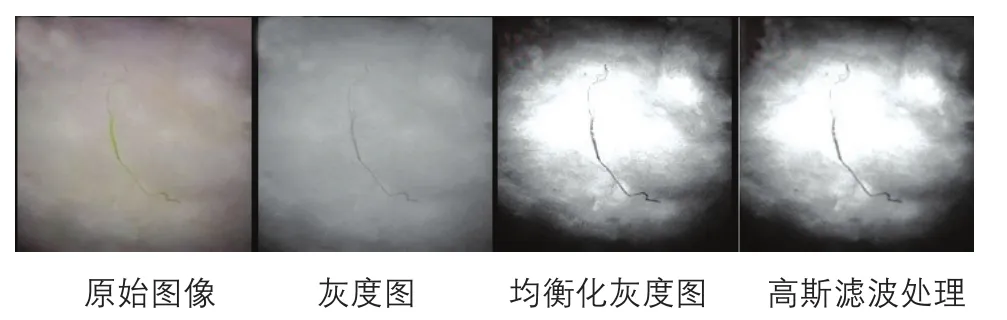
圖1 圖像預處理

圖2 直方分布圖

2.2 Gabor濾波處理

傳統基于Gabor濾波器的疵點檢測算法，一般是通過設置不同的參數組選取Gabor濾波器組，對圖像進行多個尺度和方向的濾波處理來進行特征的提取。本文在設計4方向5尺度共20個Gabor濾波器的基礎上，接著通過損失評價函數和二維熵分別對濾波器的方向和尺度進行選取，這樣對圖像特征的提取速度會大大提高，減少了算法的復雜性，同時提高了算法的時效性。

二維Gabor函數可以分解為實部和虛部，其數學表達式如式（8）和式（9）：

圖3 Gabor濾波器的實部和虛部空間模型

Gabor濾波器的實部和虛部空間模型如圖3所示。使用Gabor濾波器進行特征提取，根據實部和虛部的不同選擇，可以將提取的特征分為偶特征、奇特征和幅值特征等。偶特征為使用Gabor濾波器實部GR來對圖像進行濾波處理得到的結果，記為FR；同理，奇特征是使用虛部GI來進行濾波操作得到的結果，記為FI；而幅值特征是同時使用實部GR和虛部GI進行處理而得到的綜合結果，為FR2+FI2。本文選擇使用實部和虛部同時進行處理而得到的綜合結果，即幅值特征作為輸出響應的結果，即使用Gabor函數的實部和虛部分別與圖像進行卷積操作，然后對實部響應和虛部響應求取幅值得到總的響應結果。濾波過程如式（10），其中R（x，y）是對圖像I（x，y）的響應結果。

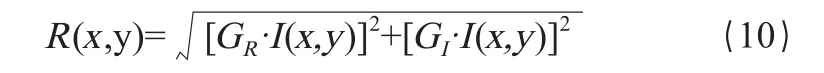
2.2.1 應用損失評價函數選取濾波器的最優方向

損失評價函數可以用來表征圖像中疵點與背景的差異化程度。首先把圖像均等地分為n塊，接著求取每一塊圖像的灰度平均值，接著分別選取出所有圖像塊灰度平均值的最大值Dmax和最小值Dmin，計算損失評價函數Q的值，如式（11）所示。

其中，Q的值與疵點和背景差異的大小呈正相關，Q越大，越容易將疵點分割出來[5]。Fdez-Valdivia在研究中提出，4個方向的濾波器已經能夠完成對圖像空間頻率變化的檢測。選取濾波器方向為0°、45°，90°、135°，可以提取圖像的水平、垂直、左右對角方向的特征[6]。在其他濾波器參數保持一致的情況下，使用4個方向上的Gabor濾波器分別對預處理后的圖像I（x，y）進行濾波處理。接著對不同方向上濾波子圖像的損失評價函數進行計算，選取對應損失評價函數值最大的方向作為Gabor濾波器的最優方向。

2.2.2 應用最小二維熵值選取濾波器最優尺度

在最優方向確定的基礎上，保持其他濾波器參數一致的情況下，使用設計好的5個不同尺度的Gabor濾波器分別對疵點圖像進行濾波處理，然后計算最優方向下不同尺度濾波子圖像的二維熵值，選取最小二維熵值對應的尺度作為Gabor濾波器的最優尺度。

3 圖像分割及形態學處理

應用最優Gabor濾波器對預圖像I（x，y）進行濾波處理后得到相應圖像R（x，y）。接著對R（x，y）進行閾值分割準確定位出疵點的位置，最后進行形態學濾波處理進行細節優化和少量誤差的剔除。

3.1 圖像分割

Otsu算法可以對圖像做精準分割，且受光照變化影響較小。首先計算出R（x，y）的灰度均值μ1，先簡單地把μ1作為初始閾值；然后μ1的小范圍鄰域內使用Otsu法搜索最優閾值[7]。算法流程如下：（1）初始閾值的確定：計算圖像R（x，y）的灰度均值μ1作為初始值。（2）給定一個松弛變量ε,ε∈Z+。（3）在范圍[μ1-ε,μ1+ε]內使用Otsu法，將目標圖像分割出來。

3.2 數學形態學處理

對于圖片中的亮細節和暗細節，可以設置適當大小的結構元素來進行消除。設置完尺度比亮細節或暗細節小的結構元素后，可以使用形態學開運算來消除亮細節，而閉運算用來消除暗細節，這樣對圖片整體的灰度值均值影響不大，同時能夠消除小的像素點，防止最后檢測結果的誤判，提高準確率[7]。經過分割后的目標圖像中存在的誤判基本都屬于亮細節，因此均采用形態學開運算濾波來進行處理。

4 試驗結果與分析

試驗分別對化纖、碎葉、棉結等幾類常見的棉花疵點進行了多組試驗測試，原棉疵點圖像大小歸一化為512×512像素，部分測試結果如圖4所示，圖4左邊為含疵點的棉花原始彩色圖像，右邊為處理完成之后最后得到的疵點結果圖。

圖4 疵點檢測結果

從試驗結果可以看出，常見的原棉疵點均可以被檢測出來，定位準確，細節丟失較少，輪廓邊緣清晰，疵點形狀可以很好地分解出來。在進行的多組試驗中，只在少部分試驗結果中出現了較多的細節丟失和疵點誤判。

5 結語

對棉花疵點的檢測是棉花加工過程中重要的環節，對棉花疵點檢測的研究有助于提高棉花的加工質量。試驗結果表明，基于Gabor函數變換的算法能較好地將常見的棉花疵點從圖片中分割出來，證明了該檢測算法具有良好的檢測效果。部分試驗中最后的結果出現了誤判以及細節的丟失，說明在參數的選擇和算法的設計上可以進行進一步的優化來提高其識別的準確率。在進行實時檢測時，Gabor算子提取特征的復雜程度較高，還需要進一步簡化、提高，所涉及的工程實際問題仍需進一步解決。